Heredity and environment interact at the level of gene expression, controlled by transcription networks, which in turn are driven by signalling pathways. Unlike metabolic pathways, what is transmitted by signalling pathways is information, not matter. Since RNA polymerase II is a limiting resource, only a fraction of the genome can be transcribed at any time. Despite the importance of signalling pathways in the control of gene expression, we know very little about their detailed kinetics. We show here that some transcription networks follow Boolean kinetics: their inputs are a combination of IF→THEN, AND, OR and NOT information and their output is either ON or OFF. A kinetic model of the lac operon in E.coli predicted Boolean kinetics. Such pathways act as monostable systems: their normal, resting state is OFF, and following an input, which may be very weak, and very transient, they amplify and prolong the signal sufficiently to activate the appropriate transcription network, after which (assuming the input signal has now ceased) they revert to the OFF state. A computer model of the MAP kinase pathway of eukaryotic cells also predicted Boolean kinetics. Cross-talk effects between signalling pathways result in the entire signalling network acting as a complex interactive system. Inhibitors of signalling pathways may have all-or-none effects on transcription, making the pharmacodynamics of these agents different from those of classical drug dose-response curves. However, a model of PI3K signalling predicted classical saturation kinetics, and inhibitors of this pathway showed conventional inhibition kinetics.
Akt signalling, boolean logic, computer models, lac operon, MAP kinase pathway, PI3 kinase pathway, signalling pathways
Chemistry is analogue: we can have more or less of a particular compound, and when that compound reacts with another, it does so at a rate described by chemical kinetics, a rate that is a continuous variable. The properties of chemical elements and compounds – their density, their refractive index, their electrical conductivity, are in general analogue properties. Biochemistry resembles the rest of chemistry in this respect. However, many biological properties are all-or-none: alive/dead; asleep/awake; male/female; benign/malignant. This binary divide is also seen at the level of ecosystems; predator/prey; parasite/host. It may seem intuitively that digital systems, which can take only one of two possible values (zero or one, true or false, alive or dead) are simpler than analogue systems that can take any of a potentially infinite number of values. In fact, in both electronics and biology, digital systems emerge from simpler underlying analogue systems. The speed that an antelope runs, and the speed at which a lion pursues it, are both measured on an analogue scale, but the pursuit will have one of only two possible outcomes. We here consider an example of biological information processing at the level of subcellular biochemistry, signal transduction. Because signalling pathways drive gene transcription, this is the critical interaction of genetics and environment. In a particular cell, at a particular time, a gene is either expressed or it is silent.
This system of symbolic logic, originated in 1854 by George Boole, deals with quantities that can have only the values of true or false, rather than the continuous variables of ordinary arithmetic. A review of the subject is available in [1]. In the 1930s, Claude Shannon first applied Boolean (digital) logic to the analysis of electronic circuits, and so laid the foundations for digital electronic design [2]. In digital electronics, signals are treated as ON or OFF, rather than as continuous (analogue) variables. The application to analysis of biological information came much later, with the realisation that neural circuits had close analogies with electronic circuits [3]. Information is processed in the nervous system by networks of neurons, each of which, at any particular time, is either charged or discharged, without a stable intermediate state. We shall here concentrate on an evolutionarily more primitive form of information processing, the control of gene expression by signalling pathways, and will show that these pathways can be described as Boolean logic circuits.
A recurring concept in Boolean logic is that of material implication: The statement A → B (A implies B) means that if A is true, then B is true. In many computer languages this is expressed as IF A THEN B. This is clearly an underlying rule of biochemical systems. In the presence of an enzyme that converts substance A to substance B, if A is present, then B will be present. Unlike chemical kinetics or enzyme kinetics, which are concerned with amounts of substances and rates of their interconversion, here we are only concerned with whether B is present (TRUE) or not (FALSE). The three basic relationships of Boolean algebra are AND, OR, and NOT. To make adenosine 5’-phosphate (AMP) in a cell, in the presence of adenosine kinase, we need its two substrates, adenosine and ATP. If both are present, AMP will be present. If either substrate is absent, AMP will be absent. In fact, in addition to this so-called salvage pathway, some cells, particularly liver cells, can make AMP by the alternative (de novo) pathway, from adenylosuccinate (SAMP), in presence of the enzyme adenylosuccinate lyase [4]. We could express this as
IF SAMP OR (adenosine AND ATP) THEN AMP
In plain language, if either adenylosuccinate or the combination of adenosine and ATP is present, then AMP will be present.
The NOT relationship occurs frequently in biochemical systems when the presence of one compound inhibits the formation of another, or represses expression of a gene. This is exemplified in our first example of a transcriptional network, the lac operon in the bacterium Escherichia coli (Figure 1), discussed below. Reading of the gene for beta-galactosidase is blocked by the lac repressor protein, so if repressor is present, then beta-galactosidase is not formed, and if repressor is absent, then beta-galactosidase will be present:
IF repressor THEN NOT beta-galactosidase.
However, if the milk sugar, lactose, is present, some of it (after conversion to a derivative, allolactose) will bind to the repressor protein, and inactivate it:
IF lactose THEN NOT repressor.
So in the presence of lactose, the lac gene will be transcribed, and beta-galactosidase, required for the digestion of lactose by the bacterium, will be switched on. Note that in biochemistry, as in Boolean logic, two negatives make a positive. Most transcriptional networks can be described in terms of the AND, OR and NOT relationships [5,6]. Other relationships exist: in a system where the output is determined by two inputs, sixteen Boolean functions are possible [7].
Before considering the complexities of gene expression in higher organisms, eukaryotes, we will consider a classical study in a prokaryote. The bacterium Escherichia coli (E .coli) lives in the human lower intestine, and obtains its food from the digestion products of our diet. Some strains of E. coli are pathogenic, particularly if they enter the blood, but most humans harbour strains of E. coli in their gut without ill-effect. The ability of E.coli to digest the milk sugar, lactose, formed one of the classic early studies of molecular biology, by François Jacob and Jacques Monod, reviewed in [8]. The biological problem to be solved here is that it is energetically inefficient for a bacterium to produce the enzymes needed to digest lactose if there is no lactose present in the environment, the growth medium. The bacterium thus needs a system to detect whether lactose is present, and to make the required enzymes if, and only if, they are needed. The first enzyme in the pathway that utilises lactose as an energy source is β-galactosidase, which cleaves the disaccharide, lactose, into the monosaccharides, galactose and glucose. Jacob and Monod showed that in the absence of lactose, E.coli did not make β-galactosidase, but were able to switch it on in the presence of lactose. The response is all-or-none, or digital, rather than a graded response where the cell makes a little β-galactosidase if there is a little lactose present, and more β- galactosidase when there is more lactose present. We cannot ask the bacterium why that is, but enzymes are catalysts, so a small amount of enzyme can transform a large amount of its substrate, and this all-or-none response is probably an energetically efficient solution to the problem. If E.coli senses lactose in the growth medium, it will use it as an energy source. When the lactose is gone, the cell stops making β-galactosidase. Having a graduated response to the lactose concentration (and the other energy sources) would require having the transcription/translation machinery spread more thinly over more of the genome at any one time.
Jacob and Monod showed that expression of β-galactosidase, and two other linked genes, galactoside permease, and an acetylase (collectively known as the lac operon) was driven by a control gene, known as the lac operator. The operator (and an upstream gene, the promoter) acts an assembly site for the RNA polymerase and accessory proteins required for the messenger RNA (mRNA) for the lac operon genes to be transcribed. If there is no lactose present in the growth medium, a protein known as the repressor binds to the operator, and inactivates it. When lactose is present, a modified form of lactose, allolactose, binds to the repressor and inactivates it, resulting in activation of the operator, and transcription of the lac operon. This method of control of gene expression, involving repression, is common in bacteria. These are other prokaryote genetic control systems where the operator is normally inactive, but requires a binding protein to activate it, a process known as induction. Note that in the logic of the lac operon, two negatives make a positive: transcription of the lac operon in inhibited by the lac repressor, and the binding of lac repressor to the operator is inhibited by binding of lactose.
Veliz-Cuba and Stigler [9] showed that Boolean models could explain bistability (i.e. the existence of stable ON or OFF states, but not intermediate states) in the lac operon. Jenkins and Macauley [10] showed that the L-arabinose operon in E. coli exhibited similar kinetics. In our present study, the kinetics of the lac operon are modelled as a system of ordinary differential equations, and the outputs of the system are shown to be either fully ON or fully OFF (Figure 1).
The reactions modelled are: v1: transcription and translation of β-galactosidase, galactoside permease and transacetylase; v2: β-galactosidase turnover; v3: hydrolysis of lactose by β-galactosidase; v4: passive diffusion of lactose across the cell membrane; v5: turnover of galactoside permease; v6: facilitated transport of extracellular lactose across the cell membrane; v7: passive efflux of lactose out of the cell. Adapted from [8,11].
A kinetic model of the lac operon
The kinetic behaviour of the lac operon was explored using the computer model, lac_sim summarised in figure 1. Details of this model are shown in the supplementary material. In the absence of lactose in the extracellular fluid, the repressor protein is tightly bound to the operator gene, which is thus inhibited. The rate of transcription of the lac operon, v1, is zero, so no mRNA is made from these genes, and no β-galactosidase protein is produced. When lactose is introduced into the extracellular fluid, there is no immediate response. Efficient transport of lactose across the bacterial cell membrane requires a carrier protein, galactoside permease, in the cell membrane. This protein is coded in the lac operon itself, so in the uninduced state, it is not present.
However, lactose is a small, neutral molecule, so even in the absence of the permease, there is a slow entry of lactose into the cell, described as v4 in figure 1. Some of this lactose, after conversion to its modified form, allolactose, binds to the repressor protein (including repressor that is already bound to the DNA of the operator). The lactose-bound form of the repressor is unable to bind to DNA, so it leaves the operator free to drive transcription of the entire operon. As a result, a small amount of β-galactosidase protein is produced, and starts to digest lactose for energy production. In addition to β-galactosidase, a small amount of the permease is also produced, and migrates to the cell membrane. Once in place, this permease catalyses the much more efficient transport of lactose into the cell (v6). The more lactose enters the cell, the more of it binds to the repressor, the greater is reaction v1, resulting in more β-galactosidase and more permease. In short, this is an example of positive feedback. The behaviour of the system, as modelled by the lac_sim computer program, is shown in figure 2. For about 10 minutes after addition of lactose to the medium, nothing happens, then over about four minutes, the system becomes completely switched on. When the lactose is removed from the growth medium after 60 minutes, the fully induced β-galactosidase continues to break down galactose, in reaction v3. After a few minutes, the concentration of lactose in the cell falls below the level required to inhibit the repressor, the now uninhibited repressor once again binds to the operator, and the entire system switches off. β-galactosidase and permease are now no longer being produced by reaction v1, and they are broken down, in reactions v2 and v5.
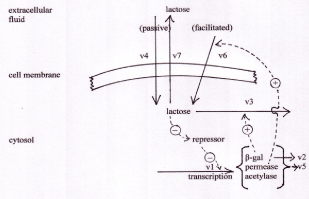
Figure 1. The lac_sim model of the lac operon
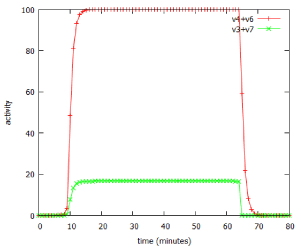
Figure 2: Switching behaviour of the lac_sim model of the lac operon.The model simulated addition of a 60 minute pulse of 1 mM lactose at time 0.
The concentration-dependence of the system is illustrated in figure 3. Low levels of lactose in the growth medium are able to passively diffuse into the cell (v4), but can equally well diffuse out of the cell (v7). This means that at low lactose concentrations (<0.15 mM according to the model), the bacterial cell is unable to accumulate enough lactose to induce the system. Figure 3 shows that above this concentration, the dose-response relationship is such that even a small additional amount of lactose causes complete activation of the system.
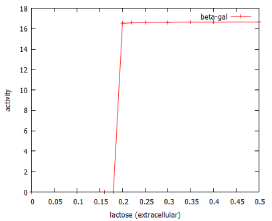
Figure 3: Dose-response curve for β-galactose induction by lactose as predicted by lac_sim Rates were assessed at 60 min after addition of lactose to the culture
It must be emphasised that the rate equations for v1 to v7 are all conventional kinetic equations in which the rate of the individual reactions is a continuous function of the concentration of the reactants. The actual equations used in the lac_sim model are listed in the supplementary material. The all-or-none kinetics of the lac operon is an emergent property of the autocatalytic relationship between intracellular lactose concentration and permease-facilitated lactose uptake.
“The activities of the transcription factors in a cell … can be considered an internal representation of the environment. For example, … E.coli has an internal representation with about 300 … transcription factors. These regulate the rates of production of E.coli’s 4,000 proteins” [12].
Organisms such as fungi, plants, and animals (eukaryotes) differ from bacteria (prokaryotes) in that their cells contain a nucleus, and their DNA (which is predominantly in the nucleus) is much more elaborately packaged with nucleoproteins. The control of gene expression in eukaryotic cells is very complex: whether or not a gene is transcribed in a particular cell, at a particular time, will depend on such factors as whether the associated histone proteins are tightly bound, excluding RNA polymerase, or whether they are more loosely attached, allowing access to the polymerase. This in turn will depend on the degree of acetylation or methylation of the histones. Whether a gene is transcribed or not will depend upon whether its promoter has been silenced by DNA methylation, and on which transcription factors and co-factors are present. Once the gene has been transcribed, whether it is expressed will depend on whether the RNA transcript has had the right post-transcriptional processing and whether the necessary factors are present for translation of mRNA to protein to occur. There are several excellent summaries of these topics [13-16]. From the perspective of information processing, we are only concerned with the question “is this gene expressed or silent?” The decision of whether a particular gene is expressed or not is driven by internal signals (what kind of cell is this? What stage of development is it at? ) and signals from outside the cell (what are the environmental conditions? What is the nutritional situation? Is the cell under oxygen stress or thermal stress?). Control of gene expression is the primary site at which heredity and environment interact [13], and is thus a major site of biological information processing. Differences between bacterial and eukaryotic signalling may be in part an adaptation to the larger size of eukaryotic cells.
Not only is the control of gene expression in eukaryotes complex, but the signalling pathways that convey information from the outside world to DNA are correspondingly complex. It is difficult to define an exact number of signalling pathways in mammalian cells, as multiple receptors may drive a common pathway, and pathways are highly branched, but if we consider a signalling pathway as involving a defined sequence of three or more components involved in one or more of the signal transduction motifs considered below, there are perhaps a dozen important signalling pathways involved in mammalian gene expression. In fact, the signalling pathways form a single highly interactive network. We will illustrate the information processing capability of the signal transduction pathways by considering two of them. The MAP kinase signalling pathway is summarised in figure 4.
The EGF receptor (EGFR) is a complex protein that spans the cell membrane. EGFR is actually a family of four closely-related receptors. Their extracellular domain is capable of binding, and being activated by, EGF, a peptide growth factor, and incidentally by a few other growth factors including transforming growth factor alpha (TGFα). “MAP” is an acronym for “mitogen activated protein”, mitogens being compounds, such as EGF, that activate mitosis, or cell division. The intracellular domain of EGFR includes a protein tyrosine kinase activity (EGFR-TK), which is active only when EGF is bound to the extracellular domain. EGFR is a dimeric protein, and when EGF is bound the EGFR-TK phosphorylates tyrosine units in the other subunit (autophosphorylation). These phosphorylated tyrosines are recognised by an adaptor protein, known in mammalian cells as Grb2 and in flies (where the signalling pathway is very similar) as SOS. When Grb2/SOS is activated in this way it activates another membrane-bound protein known as ras. Ras is a member of a family of proteins termed G-proteins, by virtue of the fact that they bind the guanine nucleotides GTP and GDP. Ras, again, is actually a family of three closely-related proteins, H-ras, K-ras, and N-ras that are functionally identical but expressed in different tissues. When ras is bound to GTP, it binds and activates a serine/threonine kinase termed raf (again, a small family of related kinases). Ras-GTP is hydrolysed to the inactive ras-GDP. The GDP in this complex is very tightly bound, and the ras can only be re-activated in the presence of Grb2/SOS, which enables it to release GDP and bind another molecule of GTP; Grb2/SOS is thus known as a GDP exchange factor. Most signalling pathways include a G-protein, for reasons we shall consider shortly. The raf protein now acts as the first stage in a three-stage kinase cascade, in which raf activates MEK, and MEK activates ERK. MEK and ERK, like raf, are protein kinases, and the significance of this three-tier cascade is that signal amplification occurs as each step, giving a very high degree of overall amplification. This means that effectively, even a minute input to the system saturates the output, which thus acts as an ON/OFF switch. In other words, the MAP kinase pathway acts as a Boolean logic circuit.
Unlike the lac operon in E. coli, where the switching behaviour was driven by a positive feedback loop, the MAP kinase pathway does not need positive feedback to act as a switch. In fact, eukaryotic signalling pathways do contain multiple positive and negative feedback loops, but rather than attempting to describe their kinetics in exact detail, the object of the present discussion is to review the general principles, and demonstrate that these complex pathways act as nature’s digital logic circuits. The final stage in the MAP kinase cascade, ERK (formerly known as MAP kinase) activates a protein, c-fos, which complexes with c-jun to form the transcription factor AP-1. AP-1 binds to DNA and drives transcription of a number of proteins, including cyclin-D, which forms part of the cellular apparatus known as the G1 checkpoint. The G1 checkpoint acts to arrest the progress of cells in G1 phase of the cell cycle (the phase immediately following cell division) until they have doubled their protein content, checked that their DNA is undamaged, and that they have sufficient purine and pyrimidine precursor molecules to start DNA replication. Cyclin D, in conjunction with the cyclin-dependent kinase, cdk4, now activates another transcription factor, E2F, which activates transcription of DNA polymerase α, and other enzymes essential for DNA replication. The cell then moves into S phase of the cell cycle. Among the transcripts driven by E2F is c-myc, a transcription factor that acts as a master regulator of cell growth, cell proliferation, cell differentiation and apoptosis. It is claimed that 15% of all genes require active c-myc for their transcription [17].
This pathway, summarised in Figure 4, has been modelled by a computer program, MAPK_SIM, which enables us to explore its kinetic behaviour. Figure 5 shows the computer’s estimates of cyclin D concentrations in cells exposed to various concentrations of EGF for 20 minutes. If the data are fitted to a form of the Hill equation [18]:
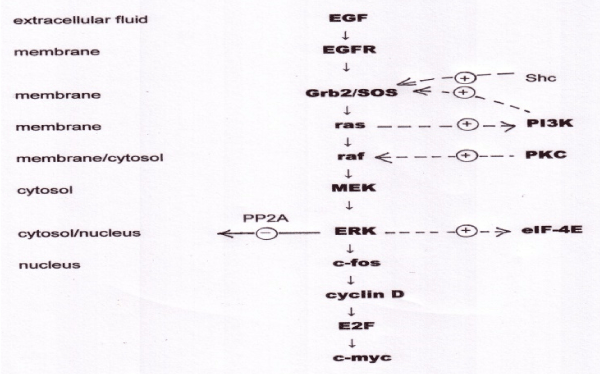
Figure 4: The MAPK_SIM model of the MAP kinase signalling pathway, showing cellular locations of components, downstream transcription factors, and cross-talk.
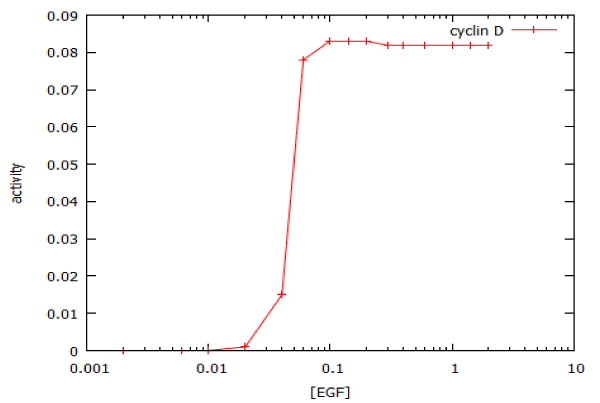
Figure 5: Dose-response curve for activation of the MAP kinase signalling pathway by epidermal growth factor (EGF). The plot shows the response to a 20’ pulse of EGF, as measured at 75 min. The calculated IC50 is 47 pM and the Hill coefficient is 10.2.
V = (EGF/Km)n . Vmax / (1 + (EGF /Km)n
where Vmax is the rate at saturating concentration, Km is the concentration of EGF that gives half-maximal rate, and n is the steepness (slope) of the dose-response curve, we obtain a value for n of 10.2. For a typical enzyme-catalyzed reaction, n = 1. For a truly all-or-none digital dose-response relationship, n = infinity. To a close approximation, we may regard the MAP kinase pathway as having Boolean ON/OFF kinetics. The functional significance of this is that a cell will either replicate its DNA at the maximum possible rate, or not at all: it cannot make DNA at half-speed.
The model predicted that a brief (5 minute) exposure to EGF was able to activate production of the downstream product of the pathway, cyclin D, for over two hours (Figure 6). In signalling terms, this is an example of pulse-expansion: signalling pathways can amplify, not only the amplitude of a signal, but also its duration.
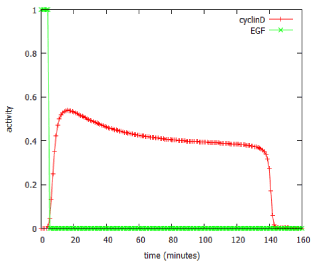
Figure 6: Use of the MAPK_SIM program to predict effect of a 5-minute pulse of EGF on expression of cyclin D.
The PI3 kinase (PI3K) signalling pathway (also known as the Akt signalling pathway) was also modelled, using a program, Akt_SIM, described in the supplementary material. The reactions included in this model are summarised in figure 7. The PI3K pathway is involved in regulation of a variety of metabolic processes, of which one of the most significant is protein synthesis. This pathway can be activated by a wide range of ligands, of which we have selected platelet-derived growth factor (PDGF) for modelling.
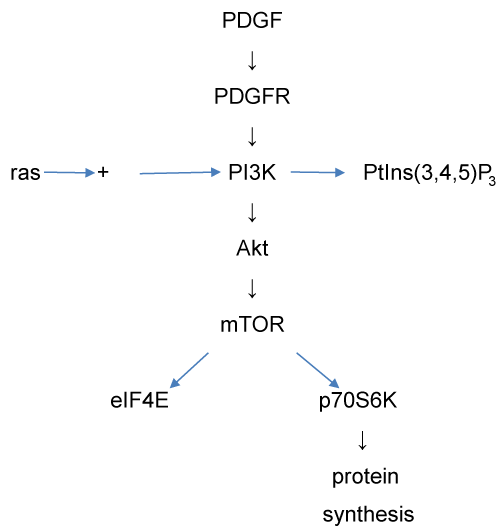
Figure 7: The PI3 kinase signalling pathway as modelled by the Akt_SIM model
Unlike the MAP kinase pathway, the dose-response curve for activation of the PI3K pathway by its activator, PDGF, does not follow ON/OFF kinetics, but shows a classical saturation curve with a Hill coefficient of 1.1 (Figure 8). However, the PI3K pathway resembles the MAP kinase pathway in that a brief exposure to growth factor causes prolonged activation (Figure 9). This is probably attributable to the fact that the PDGF receptor (PDGFR) is a G-protein-coupled receptor.
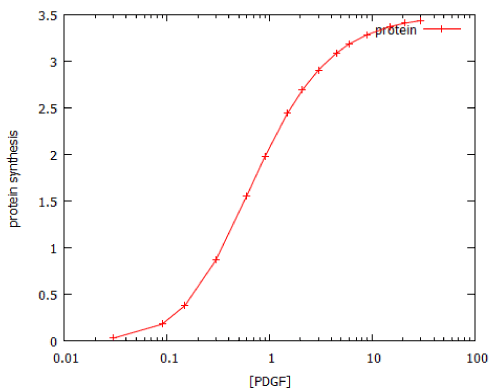
Figure 8: Dose-response curve for activation of the PI3 kinase signalling by a 20-minute pulse of PDGF
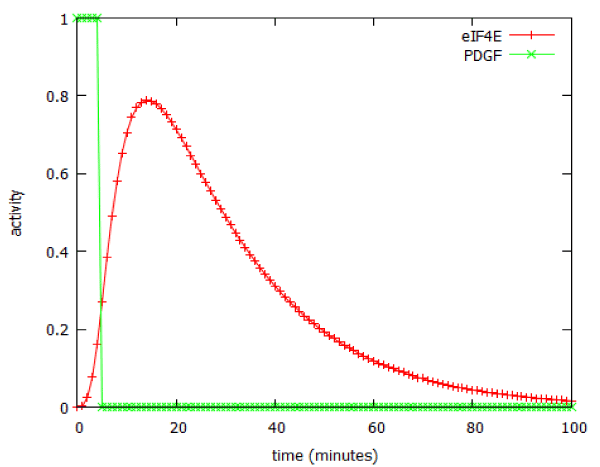
Figure 9: Prolonged activation of the PI3 kinase signalling pathway following a 5-minute pulse of PDGF.
Many important anticancer drugs act as inhibitors of signalling pathways, so it was of interest to study the effect of such inhibitors in our model pathways. We examined the effect of an inhibitor of facilitated transport on β-galactosidase expression in the lac_sim model of the lac operon, modelling a 60 minute exposure to lactose. Figure 10 shows that after an initial gradual phase, a small additional increase in inhibitor caused a precipitous decline in gene expression. Fitting the data to a Hill equation predicted a Hill coefficient (slope) of -66, almost vertical. Higher concentrations of transport inhibitor resulted in oscillations (Figure 11). The oscillations ceased when the extracellular lactose was removed, at 60 min.
Figure 12 shows the dose-response curves for two anticancer drugs that act on the MAP kinase pathway, as modelled by MAPK_sim. The calculated Hill coefficient for sorafenib was -1.0.
For erlotinib the dose-response curve was steeper, with a Hill coefficient of -2.4. The model of PI3 kinase signalling was used to predict the dose-response relationship for LY294002. This was a typical dose-response relationship, with Hill coefficient close to -1 (Figure 13).
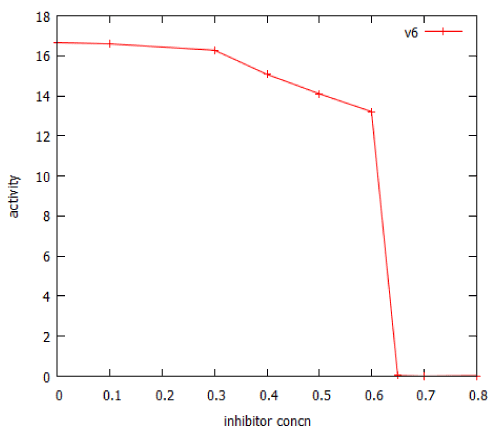
Figure 10: Dose-response curve for an inhibitor of lactose facilitated diffusion in the lac_sim model
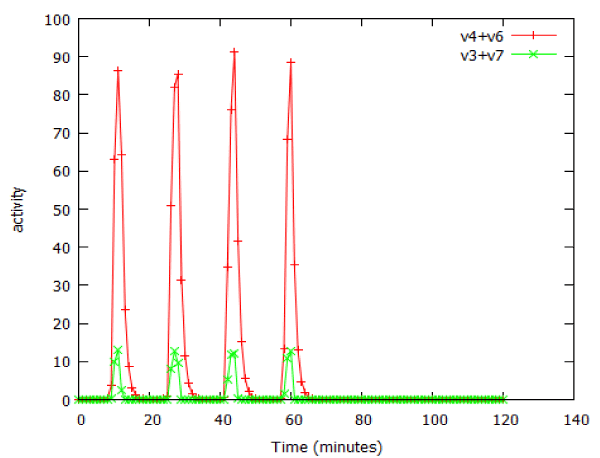
Figure 11: Oscillations in activity of the lac operon caused by an inhibitor of facilitated lactose transport, as modelled by lac_sim
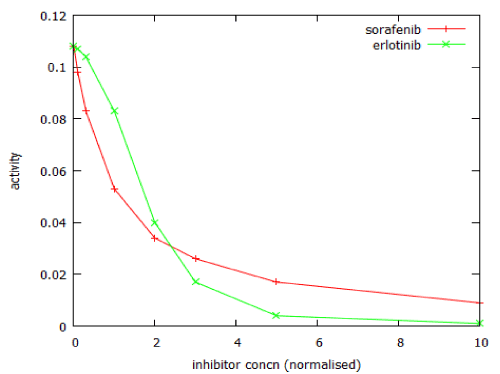
Figure 12: Comparison of the dose-response curves of two inhibitors of MAPK signalling. Inhibitor concentrations are normalised with respect to their Ki values.
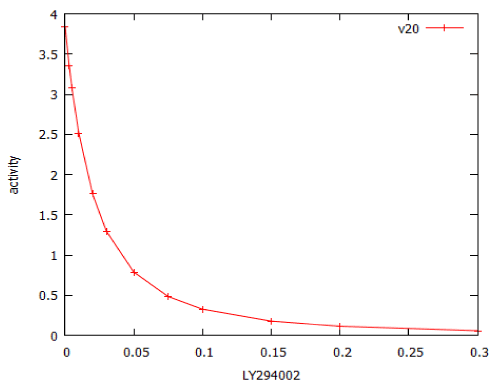
Figure 13: Dose-response curve for the PI3 kinase inhibitor, LY294002, modelled by PI3K_sim.
Why can’t an organism express all its genes all the time? As discussed in the case of E. coli, in a competitive environment this would require expending energy and nutrients to make proteins that are not needed, and this would place the organism at a competitive disadvantage to more efficient organisms. It would also limit the ability of the organism to respond to changes in the environment. Expression of a sub-set of capabilities, whether in an organism or a society, makes possible division of labour, specialisation of function. This is even more important in multicellular organisms than in bacteria. A body in which liver cells and skin cells have distinct functions is more efficient than one where specialised cells do not exist, and a society where farmers and pharmacists have distinct responsibilities is a more effective society.
Transcriptional networks and their associated signalling pathways together provide the control of gene expression. They are where the genome and the environment interact: the genome tells the organism what can be transcribed, and the environment, sensed through the signal transduction pathways, determines when, and if, the genes will be transcribed. Debates about whether particular physical or behavioural traits are primarily determined by heredity or environment are meaningless unless we know what determines whether the relevant genes are expressed, in which cells, at what time.
Information processing by signalling/transcription networks involves nine recurring features:
- Translocation. Typically, environmental signals activate receptors on the cell surface, and the signal is relayed through the cytosol, to the nucleus. Some hormones (steroids, thyroid hormone) are able to cross the cell membrane and enter the cytosol. Their receptors, thus activated, then enter the nucleus and act as transcription factors. Most signals, however, are transmitted by proteins, or peptides, or electrically-charged small molecules that are unable to enter the cell, so that more elaborate signalling pathways are required.
- Signal amplification. As Claude Shannon demonstrated with telecommunications, conducting a message over even a short distance inevitably involves loss of signal, a consequence of the second law of thermodynamics. Thus signal amplification is usually necessary. This is usually achieved in living systems by cascades of protein kinases, where one molecule of protein kinase A phosphorylates and activates multiple molecules of protein kinase B, which in turn can activate many molecules of kinase C. The MAP kinase pathway provides a classic example of a three-stage amplifier.
- Pulse expansion. Biological signals are often not only faint, but transient, needing expansion in duration, as well as amplitude, if they are to get their message through. Transcription often acts on a time-scale of a few minutes to a couple of hours. Most signalling pathways in eukaryotic cells achieve this pulse expansion through G-proteins, whose kinetic properties enable them to act as monostable circuits with relaxation times having the appropriate time constant. As an example of this, the MAPK_SIM model of the MAP kinase pathway was used to model the response of a cell to a 5 minute pulse of EGF (Figure 6). Cyclin D levels rose rapidly and remained elevated for over two hours after the EGF had gone away.
- AND gates (convergent branching). Some genes should only be transcribed when two or more conditions are met. An example from developmental biology is that many cells will only enter cell division if they are in the right place. The signalling pathways that trigger cell division require a growth signal (e.g. from a growth factor receptor) AND an attachment signal (e.g. from an integrin).
- OR gates. Another form of convergent branching is where any of two or more inputs can trigger a particular output. An important example of OR gates in signal transduction is where a common signalling pathway may be driven by a number of receptors. For example, we have modelled the PI3 kinase pathway as driven by PDGF, but it is also activated by insulin, insulin-like growth factor-1(IGF-1) and vascular endothelial growth factor (VEGF).
- Divergent branching (multiplexing). A dozen or so signalling pathways determine the activity of a thousand or more transcription factors. It follows that the pathways are highly branched. The same pathways may activate different transcriptional networks in different cell types, or in the same cells at different stages of their life cycle. Which branches are active under various conditions are determined by a complex system of feedback effects.
- Negative feedback. Feedback effects operate at all stages of signalling, from membrane receptors to transcription factors. Feedback not only ensures a signal of appropriate amplitude, but also controls timing. A common motif is that a particular transcription network activates an inhibitor of an upstream process, but with a time delay.
- Positive feedback. Positive feedback is the hallmark of switching systems, that may have multiple steady states. The lac operon, in which the presence of lactose in the bacterial cell switches on galactoside permease, which in turn greatly increases the entry of lactose into the cell, is a classic example of this. Positive feedback is the primary determinant of the Boolean, rather than analogue, logic that describes transcription netwoks.
- Cross-talk. Signalling pathways regulate morphogenesis, cellular metabolism, damage responses, cell division, and specialised cell functions such as those of the nervous and immune systems. Clearly these systems have multiple, complex interactions. Cross-talk may be one-way or two way. When a cell is making DNA, it has requirements for extra protein, so the MAP kinase pathway generally switches on the PI3K pathway. However, there are conditions where the cell needs to make protein without making DNA, so activation of the PI3K pathway does not necessarily activate the MAP kinase pathway. Activity of the various transcriptional networks acts in effect as a map of the cellular environment, a primitive form of pattern recognition, and this is achieved largely by cross-communication between signalling pathways.
As we have seen in the study of the lac operon in E. coli, and of the MAP kinase pathway in eukaryotes, despite the great complexity of transcription networks and signal transduction pathways, gene expression can often be considered as an all-or-nothing process: a gene is either transcribed or it is silent. This is a consequence of the amplifier kinetics and of (minimally) a positive feedback loop involving ras. There are regulatory processes by which the cell can determine how much of a particular protein should be made, but running gene expression at half-speed does not seem to be an option, at least in the examples we have studied. For this reason, it seems to be a valid approximation to describe transcription networks as Boolean logic circuits.
Analogue signal processing is in some senses more primitive than digital: e.g. the Michaelis equation is simpler than the equation for an ON/OFF system. This example of simplicity emerging from apparently more complex origins is mirrored in the history of electronics, where digital circuits, accurately described by Boolean algebra, have been developed from underlying analogue devices. Information is processed at the level of gene expression in response to a wide range of stimuli. We have considered a nutritional stimulus in the case of E. coli, and the example of growth factor signalling in eukaryotes.
Why do some signalling pathways (lac, MAPK) show Boolean kinetics while others (PI3K) show saturation kinetics? In the case of the MAPK pathway, which primarily drives DNA synthesis, DNA must either be made in a fixed amount (i.e. to double the existing DNA content) or not at all. By contrast, the PI3K pathway primarily regulates protein synthesis, and protein may be required in varying amounts, depending upon the nutritional status of the cell. Inhibitors of the PI3K pathway were predicted by the model to have conventional dose-response curves. Inhibitors that act at sites of positive feedback have been previously reported to show switching behaviour, with very steep dose-response relationships, and in some cases oscillations [19, 20]. Both were seen in our lac_sim model (figures 10, 11). In the MAP kinase pathway, although the kinetic behaviour closely approximates a Boolean system, this appears to be the result of a saturated output from a three-stage amplifier, rather than from positive feedback. Modelling inhibitors of two components of the pathway predicted classical Hill kinetics (figure 12), though it is interesting that erlotinib, acting upstream of the kinase cascade, was predicted to have a much steeper dose-response curve than sorafenib, which inhibits one of the kinases in the amplifier cascade, Steep dose-response curves confer greater selectivity on inhibitors [19]. Understanding the kinetics of signalling pathways may help us to use inhibitors of these pathways more effectively, and kinetic models of these pathways are a valuable tool for such analysis.
The signalling pathways summarised in figures 1, 4 and 7 were modelled as systems of ordinary differential equations (ODEs), in which the state variables were the substrates and signalling molecules shown in those figures, connected by rate equations. Details of the ODEs and rate equations are given in the supplementary material. The model of the lac operon was based upon [8,9] and [11]. The model of MAP kinase signalling is based upon that of Brightman and Fell [21], and the model of PI3K signalling was adapted from [22]. The models were coded in the C programming language and compiled using the GNU compiler collection (gcc) release 4.6.2. ODEs were solved using the 4th-order Runga-Kutta algorithm [23]. Hill coefficients were calculated by nonlinear regression using the program DRFIT, described in [18]. Graphics were plotted using gnuplot [24].
View supplementary data
2021 Copyright OAT. All rights reserv
- Givant S, Halmos P (2009). Introduction to Boolean Algebras. Undergraduate Texts in Mathematics. Springer, ISBN 978-0-387-40293-2.
- Shannon C (1949) The synthesis of two-terminal switching circuits. Bell System Technical Journal 28: 59-98. doi: 10.1002/j.1538-7307. 1949.tb03624.x
- Caudill M, Butler C (1992). Understanding Neural Networks: Computer Explorations, Volumes 1 and 2. Cambridge Mass. MIT Press.
- Jackson RC (1987). Computer simulation of the effects of antimetabolites on metabolic pathways. In “New Avenues in Developmental Cancer Chemotherapy” (editors KR Harrap and TA Connors), pp.3 – 35), Academic Press, Orlando, Florida.
- Xiao Y. A tutorial on analysis and simulation of Boolean gene regulatory network models. Curremt Genomics 2009; 10: 511-525.
- Simak M, Yeang CH, Lu HH (2017). Exploring candidate biological functions by Boolean function networks for Saccharomyces cerevisiae. PloS One 2017 Oct 5; 12(10): e0185475. doi: 10.1371/journal.pone.018475.
- Kauffman S (1995). At Home in the Universe, p.105. Oxford University Press.
- Akusjärvi G (1995). Gene expression, regulation of, in “Molecular Biology and Biotechnology: A Comprehensive Desk Reference (edited by RA Meyers) pp. 346-350. New York, VCH Publishers.
- Veliz-Cuba A, Stigler B (2011). Boolean models can explain bistability in the lac operon. J Comput Biol 2011 Jun; 18(6): 783-794.
- Jenkins A, Macauley M (2017). Bistability and asynchrony in a Boolean model of the L-arabinose operon in Escherichia coli. Bull Math Biol 2017 Aug; 79(8): 1778-1795.
- Keen RE, Spain, JD (1992). “Computer Simulation in Biology”, p. 354. Wiley.
- Alon U (2007). “An Introduction to Systems Biology: Design Principles of Biological Circuits”, London, Chapman & Hall.
- Latchman DS (2008) “Eukaryotic Transcription Factors” (5th edition), Academic Press.
- Gomperts BD, Kramer IM, Tatham PER (2002). “Signal Transduction”, Amsterdam, Elsevier.
- Nelson J (2008). “Structure and Function in Cell Signalling”, Wiley.
- Hancock JT (2010). “Cell Signalling” (3rd edition), Oxford University Press.
- Pelengaris S, Khan M, Evan G (2002). c-Myc: more than just a matter of life and death. Nature Reviews, Cancer 2: 764-776. doi: 10.1038/nrc904.
- Jackson RC (2016). Seven Equations of Life: The Fundamental Relationships of Biomathematics, Lambert Academic Publishing.
- Jackson RC (1993). The kinetic properties of switch antimetabolites. J Natl Cancer Inst 85(7): 539-545.
- Pfeuty B, Kaneko K (2009). The combination of positive and negative feedback loops confers exquisite flexibility to biochemical switches. Phys Biol 6(4): 046013. doi: 10.1088/1478-3975/6/4/016013.
- Brightman FA, Fell DA (2000). Differential feedback regulation of the MAPK cascade underlies the quantitative differences in EGF and NGF signalling in PC12 cells. FEBS Lett. 482, 169–174.
- Jackson RC, DiVeroli GY, Koh SB et al. (2017). Modelling of the cancer cell cycle as a tool for rational drug development. A systems pharmacology approach to cyclotherapy. PloS Comput Biol 2017; 13(5): e1005529. doi: 10.1371/journal.pcbi. 1005529.
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP (2007). Numerical Recipes in C: The Art of Scientific Computing, 3rd edition. Cambridge University Press.
- Janert P (2010). Gnuplot in Action. Understanding Data with Graphs. Manning Publications Co.
- Hanafusa H, Torii S, Yasunaga T, Nishida E (2002). Sprouty1 and sprouty2 provide a control mechanism for the Ras/MAPK signalling pathway. Nature Cell Biol 4(11); 850-858.
- Xu MJ, Johnson DE, Grandis JR (2017). EGFR-targeted therapies in the post-genomic era. Cancer Metastasis Rev 2017, Sep 2. doi: 10.1007/s10555-017-9687-8.
- Wilhelm S, Chien DS (2002). BAY 43-9006: Preclinical data. Curr Pharm Des 8(25): 2255-2257. Review.
- Vlahos CJ, Matter WF, Hui KY, Brown RF (1994). A specific inhibitor of phosphatidylinositol 3-kinase, 2-(4-morpholinyl)-8-phenyl-4H-1-benzopyran-4-one (LY294002). J Biol Chem 296: 5241-5248.













