Abstract
Tumor glycolysis is a self-organized nonlinear mechanism that can exhibit oscillations under certain conditions. Experimental evidence suggests that glycolytic oscillations may give certain advantages to cancer, including resistance to therapies. A previously developed oscillating glycolysis model was modified with the objective of theoretically evaluating the effect of pulses and periodic glucose deprivations in a frequency range that included values close to the autonomous frequency. The dynamics of the model before the perturbation were characterized. Then the model was perturbed with periodic pulses and deprivations of glucose. The dynamics obtained were characterized and compared with the model before the perturbation. The methods for the characterization of the dynamics were: stability analysis of the steady state, stroboscopic analysis and Lempel-Ziv index; while the cellular energy charge of the simulations was evaluated by the normalized ATP/ADP ratio. The results obtained indicate that periodic glucose pulses can lead to an increase in the energy charge. Surprisingly, sustained increases in glucose influx causes a decrease in the complexity of glycolytic oscillations, but cause increase in the cellular energy charge. On the other hand, periodically depriving the tumor microenvironment of glucose at high perturbation frequencies, regardless of the amplitude of perturbation, prevent the increase in the complexity of glycolytic oscillations and cause a decrease in the cellular energy charge of tumor cells. This strategy can increase the efficacy of antitumor therapies.
Introduction
The most frequent metabolic alteration in most tumors is the high consumption of glucose and the excretion of large amounts of lactate even under aerobic conditions, a phenomenon known as the Warburg effect [1]. The high glycolytic rate provides metabolic energy and the biosynthesis precursors required for cell proliferation [2].
The increased glycolytic flux in tumor cells is due to the over-expression of glycolytic enzymes and transporters [3] induced by the activation of various oncogenes and the Hypoxia Induced Factor (HIF-1α) [4]. This regulation of metabolism has been related to an increase in tumor aggressiveness [5]. Thus, the glycolytic phenotype plays a role in the progression of neoplastic cells [6].
Tumor glycolysis can oscillate under certain conditions, which has been demonstrated in cells that develop a hypoglycemic phenotype [7-9]. This phenomenon is verified through temporary oscillations in the concentration of glycolytic intermediates. Experimental evidence suggests that these oscillations may give certain advantages to cancer, including resistance to therapies [8]. In fact, it is known that periodic behavior gives biological systems certain properties such as greater adaptability, synchronization possibilities and greater resistance to fluctuations and environmental perturbations [10].
It has been shown that the complexity of tumor glycolysis in the hypoglycemic state is superior to a hyperglycemic state [11]. Experimentally, it has been proved that in hypoglycemic states the tumor glycolysis exhibits an increase in the levels of glucose transporters 1 and 3 (3,4 and 2,1-fold, respectively) and hexokinase I (2,3-fold) compared to the hyperglycemic standard cell culture condition [3]. Furthermore, a correlation between increased glycolysis and tumor resistance to chemo- and radiotherapy has been found [3,12]. These studies suggest that there is a positive correlation between complexity and resistance. In fact, resistance to external perturbation may increase with increasing complexity in oscillations [13]. Therefore, more complex tumor glycolytic oscillations can be associated with greater resistance to external perturbations aimed at affecting this metabolic pathway. This increases the robustness of the system. According to Kitano, robustness is a property that allows a system to maintain its function against internal and external perturbation [14].
Cancer glycolysis is a self-organized process far from thermodynamic equilibrium [15]. This metabolic network is characterized by a synchronization of individual reactions under a nonlinear dynamic [16] that exhibits feedback loops through enzymatic regulation [17]. Under these conditions the system can exhibit oscillations [13]. These premises led us to consider the following hypothesis: the degree of self-organization achieved by tumor glycolysis can be affected by the application of periodic glucose perturbations simulating a chronotherapeutic regimen. This kind of perturbation could influence the complexity of glycolytic oscillations and energy metabolism of the tumor cell, which would affect its resistance to therapies.
Chronotherapy is defined as a temporarily adequate medical treatment that takes into account the biological rhythm of the organism and guarantees greater efficacy in its application [18,19]. The effect of periodic pulses of glucose has been experimentally evaluated in yeast [20,21], however to our best knowledge there are no such experiences in oscillating tumor glycolysis. On the other hand, the effect of periodic nutrient deprivation in cancer has been studied and encouraging results have been obtained [22]. That study, being experimental, only represents perturbation periods much longer than the autonomous period of oscillating tumor glycolysis, which is of the order of tens of seconds [9]. Mathematical modelling allows us to explore what could happen if the perturbation and the tumor oscillation were of the same order.
Recently, a mathematical model was proposed to describe qualitatively the autonomous glycolytic oscillations found experimentally in tumor cells [15]. The goal of this work is to evaluate the effect of periodic pulses and deprivations of glucose at frequencies near the autonomous frequency of oscillating tumor glycolysis. The manuscript is organized as follows: In Section 2, we propose modifications to the previous glycolytic model [15] and a mathematical function for describing the perturbation. Section 3 is devoted to the analysis of the autonomous system and to the characterization of the perturbed model with periodic pulses and deprivations of glucose. Section 4 comprehends the discussion of the results. Finally, some concluding remarks are presented in Section 5.
Methods
A biochemical network model of glycolytic oscillations
The kinetic model proposed by Martin et al. [15] adapted to hypoglycemic HeLa cells was modified. However, the basic mechanism of the glycolytic pathway was maintained as illustrated in figure 1.
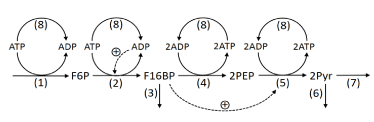
Figure 1. Representation of the kinetic model of glycolysis, adapted to HeLa tumor cells
It was obtained from the adjustment of the model proposed by [15]. Dashed lines indicate activation of enzymes by metabolites. Reaction 1: GLUT + HK + HPI; reaction 2: PFK-1; reaction 3: non-glycolytic consumption of F1,6BP; reaction 4: ALDO + TPI + GAPDH + PGK + PGM + ENO; reaction 5: PYK, reaction 6: MCP (mitochondrial consumption of pyruvate); reaction 7: LDH; reaction 8: ATPase.
Reaction 1:
The HK reaction was replaced by another one that includes in a single step the effect of the glucose transporters expressed in HeLa and the reactions catalyzed by HK and HPI. The proposed rate law is described as:
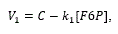
where C represents a constant flux and can be interpreted as the transport rate of glucose from the extracellular medium to the intracellular one; while ki is a rate constant.
Reaction 2 (PFK-1):
F1,6BP was included as a product that activates the enzyme PYK. The basic structure of the equation used by Martin et al. [15] which considers the activation by product (ADP) of PFK-1 was maintained. Unlike the previous model [15], it was considered that the rate law depends on the F6P substrate. This is possible using the equation proposed by Goldbeter and Dupont [23].
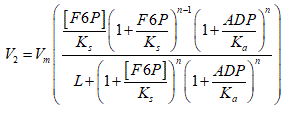
Vm is the maximum rate of the catalyzed reaction, denotes the number of subunits of the enzyme, Ks is the dissociation constant of the substrate to the relaxed state of the enzyme, Kα is an activation constant and L is the allosteric constant [24].
Reaction 3
A reaction representing the consumption of F1,6BP was added through a non-glycolytic mechanism, which agree with previous works [25]. This was done in order to avoid a sustained increase of F1,6BP.
V3=k3[F1,6BP]
Reaction 4:
The GAPDH reaction was replaced by another one that includes in a single step the effect of the reactions catalyzed by ALDO, TPI, GAPDH, PGK, PGM and ENO. The flux for this step was modified to a mass action law. To achieve the characteristic carbon balance of glycolysis, it was taken into account that for each mole of F1,6BP consumed, two moles of PEP are formed. To simplify the equation, the presence of inorganic phosphate and the NAD+/NADH system was not considered, as had been done in previous works [26].
V4=k4[F1,6BP]([ADP])2
Reaction 5 (PYK):
The rate law of the reaction catalyzed by PYK was replaced by the one proposed by Dynnik and Sel'kov [25] which considers the activation of this enzyme by F1,6BP. This guarantees the coupling between PYK and PFK-1. The rate law is described as:
V5=k5[PEP][ADP](z+([F1,6BP]/Ka)γ)
where γ is the order of activation of the enzyme by F1,6BP; z << 1 is a dimensionless parameter that determines the relative activity of the enzyme to [F1,6BP] = 0 [25].
Pyr consumption reactions
MCP and LDH represent the consumption of Pyr in the mitochondria and the cytosol respectively. The first is represented by a flux constant and the second by a mass action law [26].
V6=C1
V7=k7[Pyr]
where C1 represents a constant flux.
Reaction 8 (ATPase)
The kinetics of the reaction catalyzed by ATPase defined as a process of cellular consumption of ATP was taken as a law of mass action, which coincides with Termonia and Ross [26] and Marín et al. [3,27].
V8=k8[ATP]
The consumption and production of ATP was adjusted in reactions 1, 2 (PFK-1), 4 and 5 (PYK), to yield a gain of two moles for each inverted mole, as it occurs in the glycolytic pathway. This constitutes an autocatalytic element that can lead to oscillations [28]. Table 1 shows the values of the parameters of each rate law used.
Table 1: Values of the kinetic parameters used in the glycolytic model
Reactions |
Kinetic parameters |
References |
1 |
C = 0,0325 mM min-1 |
(a) ɸ |
- |
k1 = 0,00014 min-1 |
(a) |
- |
2-PFK1 |
Vm = 0,04 mM min-1 |
|
[3] |
n = 4 |
|
[29,30] |
L = 5,6 * 106 |
(b) |
[23] |
Ks = 1 mM |
(a) |
- |
Kα = 1 mM |
(a) |
- |
3 |
k3 = 0,0079 min-1 |
(a) |
- |
4 |
k4 = 0,000154 mM-2 min-1 |
(a) |
- |
5- PYK |
k5 = 0,001 mM-1 min-1 |
(a) |
- |
z = 0,01 |
|
[25] |
Kα = 2 mM |
|
[31] |
γ = 4 |
|
[25] |
6- MCP |
C1 = 0,0001 mM min-1 |
(c) |
- |
7- LDH |
k7 = 0,0003 min-1 |
(c) |
- |
8- ATPase |
k8 = 0,0026 min-1 |
(a) |
- |
proposed value; (b) value of L corresponds to a region of instability of the steady state in the curve: nH (Hill coefficient) vs L, when n=4 (c) values selected so that the LDH flux >> MCP flux, which is generic in tumor cells [27]; ɸ was considered as a physiological flux of glucose.
Oscillating tumor glycolysis was modeled through the following Ordinary Differential Equations System (ODES):
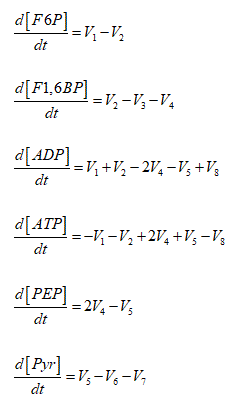
The initial concentrations of F6P; F1,6BP; ADP; ATP; PEP and Pyr used in the model were: 1,6 ; 0,5 ; 2,4 ; 14,5 ; 0,5 and 3 mM respectively. These values were obtained experimentally from HeLa cells adapted to hypoglycemic conditions [3].
The kinetic model described above constitutes a dynamic autonomous system because the rate of the reactions does not depend on time explicitly [32]. C was identified as a control parameter because it has been proposed as the most important parameter controlling the oscillations [33] and it can be modified experimentally with increases or decreases in extracellular glucose concentration.
In order to characterize the dynamics of the autonomous system (non-perturbed model) the parameter C was modified in the interval (0 – 0,5) mM min-1 and the stability of the stationary states was determined using the standard procedure [10]. The time series obtained were classified according to the dynamic response exhibited.
Additionally, the cellular energy charge was estimated from the ATP/ADP ratio for each value. This index has been previously used by other authors to estimate cellular energy level [26]. For an oscillatory dynamic, a mean ATP/ADP ratio was obtained, based on the mean of the concentrations of ATP and ADP. This value was normalized in percent with respect to the ATP/ADP ratio corresponding to C = 0,032 mM min-1. For steady state dynamics, the same procedure was performed, with the exception of the calculation of the mean.
Therefore, normalization values greater than 100% reflect an increase in cellular energy charge and lower values, a decrease. The increase in cellular energy charge activates the metabolic pathways of biosynthesis, which favors cell proliferation [17].
Periodic perturbation of the autonomous model: non-autonomous model
Parameter C was set at 0,0325 mM min-1 a value where the system exhibits sustained periodic oscillations. It was considered that this value represents a physiological flux of glucose, based on the conjecture of Fru et al. [8], who stated that glycolytic oscillations could occur in vivo tumors. Then a periodic perturbation was applied to the autonomous model (2.1). Specifically, the glucose influx: C (right member of V1) was modified by adding the following expression:
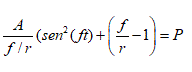 (2.2)
(2.2)
where A and f are the amplitude and the frequency of the perturbation respectively, t denotes the time of the modeling and r is a constant that represents the minimum frequency that will be used in the perturbation.
The expression (2.2) is useful to evaluate the effect of periodic glucose perturbations on the oscillating tumor glycolysis. This expression only makes sense when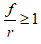 . Three cases can be analyzed:
. Three cases can be analyzed:
When 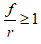 the P function takes the particular form used by other authors [34,35]:
the P function takes the particular form used by other authors [34,35]:
Asen2 (fπt) = P
which can be used to represent the situation in which glucose is supplied at a rate (Vs) lower than the rate (C) with which the tumor cell transports it to its interior: Vs < C. As a consequence C oscillates between the level basal (C = 0,0325 mM min-1) and the maximum rate reached for that perturbation without "accumulation" occurring. It can also be used when glucose is deprived at a lower rate than the rate with which the organism is able to reestablish its levels. These two situations occur when the frequency of perturbation is much lower than the autonomous frequency of oscillation of tumor glycolysis.
When 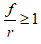 , the P function can be used to simulate frequencies near to the autonomous frequency of oscillation of tumor glycolysis. Physically, this means that Vs > C. In correspondence, accumulation occurs and does not tend to its basal level but oscillates between rates higher than the basal rate and the maximum rate corresponding to that perturbation. As the frequency rises, the minimum rate approaches the maximum rate. It can also be used when glucose is deprived at a higher rate than the rate at which the organism is able to reestablish its levels.
, the P function can be used to simulate frequencies near to the autonomous frequency of oscillation of tumor glycolysis. Physically, this means that Vs > C. In correspondence, accumulation occurs and does not tend to its basal level but oscillates between rates higher than the basal rate and the maximum rate corresponding to that perturbation. As the frequency rises, the minimum rate approaches the maximum rate. It can also be used when glucose is deprived at a higher rate than the rate at which the organism is able to reestablish its levels.
When 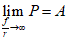 . In this case, the minimum rate of glucose influx tends to the maximum rate and a constant glucose influx is established. This flux is greater than the basal rate of glucose input. Physically, the constancy in this rate is due to the fact that a balance is reached between the rate of glucose influx in the tumor cell and the glucose consumption rate by non-tumor cells in the microenvironment. This prevents the sustained increase of glucose influx. When glucose is deprived with an infinite frequency, the constancy in the flux is due to a balance between the rate of glucose influx in the tumor cell and the rate with which the organism is able to reestablish its levels. In this case, the flux is lower than the basal rate of glucose input. This prevents the sustained decrease of glucose influx.
. In this case, the minimum rate of glucose influx tends to the maximum rate and a constant glucose influx is established. This flux is greater than the basal rate of glucose input. Physically, the constancy in this rate is due to the fact that a balance is reached between the rate of glucose influx in the tumor cell and the glucose consumption rate by non-tumor cells in the microenvironment. This prevents the sustained increase of glucose influx. When glucose is deprived with an infinite frequency, the constancy in the flux is due to a balance between the rate of glucose influx in the tumor cell and the rate with which the organism is able to reestablish its levels. In this case, the flux is lower than the basal rate of glucose input. This prevents the sustained decrease of glucose influx.
If the expression (2.2) is incorporated into ODES (2.1) through a sum, then it represents periodic pulses of glucose. On the other hand, if it is inserted as a subtraction, then it implies periodic deprivations of glucose. In both cases it is considered that the external glucose is consumed by tumor cells and by others that are contained in the tumor microenvironment.
The values of used in the simulation of pulses and periodic glucose deprivations are equivalent to 0,1 f0 and 0,2 f0 respectively, where f0 is the autonomous frequency of the system (frequency at which species oscillate in the autonomous system for C = 0,0325 mM min-1.
The dynamic responses of the perturbed system are represented in a two-dimensional bifurcation diagram, for each pair [f/r; A] imposed. In this case f/r and A constitute the control parameters. The time series obtained were classified from a stroboscopic analysis [10]. Additionally, the cellular energy charge was estimated from the percentage normalization of the ATP/ADP ratio. For this purpose, the value of the ATP/ADP ratio of the autonomous system corresponding to C = 0,0325 mM min-1 was taken as reference.
Mathematical procedure
The ODES (2.1) was solved with software COPASI v.4.6 (Build 32) [36]. The numerical method used was Deterministic (LSODA) with a relative and absolute tolerance of 10-6 and 10-12 respectively. The variation of the control parameters allowed establishing regions with different complexity. For each region, the complexity of glycolytic oscillations was quantified from the LZ index, using the algorithm LZ - 76 [37]. This index was calculated from the ATP time series because the dynamics of a species is enough to represent the dynamics of the whole system [38]. ATP time series was previously coded to a binary sequence, according to the following criterion: if the ATP concentration value is greater than the previous one, it was replaced by 0 or 1 if else, so that the first number in the series was not encoded. The expression used to calculate the LZ complexity was:
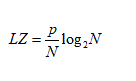 (2.3)
(2.3)
where p is the number of different patterns detected in the binary sequence and N denotes the number of points in the series.
Since the equation (2.3) is affected by the value of N, the LZ index was normalized using the equation proposed by [39]:
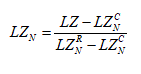 (2.4)
(2.4)
where LZNC and LZNR are the LZ values measured for a constant series (consisting of a single value repeated N times) and random (white noise) respectively, with the same number of points, N. So LZN is almost independent of the length of the series [39].
Results
Characterization of the autonomous system
The variation of the control parameter C showed that the sustained periodic behavior occurs in a range of glucose input rate limited by two critical values (0,02 and 0,15 mM min-1 approximately). According to Fru et al. [8] this oscillatory domain could be within the physiological range. Values of C less than the lower limit or greater than the upper limit lead the system to a stable steady state.
Table 2 shows the normalized ATP/ADP ratio and the LZ complexity values associated with each region. In the stable steady state region, LZ values close to 0 were detected, while higher values were found in the limit cycle. These dynamic responses were corroborated with a stability analysis of the stationary states.
Table 2. Complexity and energy charge of the autonomous system corresponding to values of contained in each of the indicated regions
| |
C (mM min-1) |
LZ |
Normalized ATP/ADP ratio (%) |
SS1 |
0 |
0 |
0 |
0.01 |
0 |
43 |
LC |
0,0325 ɸ |
0,003 ɸ |
100 ɸ |
0,005 |
0,004 |
115 |
0,008 |
0,005 |
117 |
SS2 |
0,18 |
0 |
117 |
0,5 |
0 |
117 |
SS1: Stable Steady State obtained for C values lower than the lower limit of the oscillatory domain; SS2: Stable Steady State obtained for C values greater than the upper limit; LC: Limit Cycle; ɸ value corresponding to the fixed glucose flux.
The results obtained indicate that the transition from LC to SS2, due to the sustained increase in glucose influx, can lead to a decrease in robustness, but can increase cellular energy charge in tumor cells (Table 2). This transition far from thermodynamic equilibrium is a consequence of bifurcations. In fact, cancer glycolysis behaves according to the rules of a ‘‘first order’’ phase transition [15].
Taking into account these results, a metabolic therapy is effective when it is oriented in two directions: decrease the cellular energy charge and the robustness of the tumor, or at least prevent the increase of these two factors. Precisely, the transition from LC to SS1 due to the sustained decrease in glucose influx, can lead to a decrease in cellular energy charge and robustness in tumor cells (Table 2). This can be achieved by directly attacking the degree of vascularization of the tumor.
Periodic glucose pulses
Figure 2 shows the bifurcation diagram resulting from the perturbation of the model with periodic pulses of glucose. Three regions are defined: zone without chemical sense (I), period-k and quasiperiodicity (II) and period-k (III), where k represents the ratio between the response period and the period of perturbation.
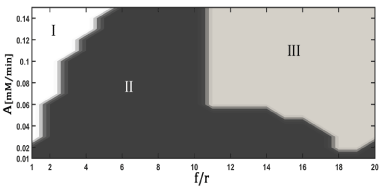
Figure 2. Bifurcation diagram for the perturbed glycolytic model with periodic pulses of glucose
A : Amplitude of Perturbation, f/r: Ratio between the frequency of perturbation and the minimum frequency used in the perturbation. Region I : Zone without chemical sense (negative concentrations of the intermediaries); Region II : period-k and quasiperiodicity; Region III : Period-k. The dynamic responses were classified from stroboscopic analysis
Region II exhibits dynamics with greater complexity than region III and the autonomous system (Table 3). Therefore, in region II there is an increase in the robustness of the tumor. This implies that this zone should be avoided from a therapeutic point of view. It is notorious that for small values of A, regardless of the value of f/r, the system exhibits a highly complex dynamic (Figure 2: región II).
Table 3. Complexity and energy charge of the perturbed glycolytic model with periodic pulses of glucose
Region |
LZ |
Normalized ATP/ADP ratio (%) |
Autonomous model (A=0) |
0,003 ɸ |
100 ɸ |
II |
0,02 |
112 |
0,02 |
117 |
0,01 |
110 |
III |
0,004 |
117 |
0,004 |
116 |
0,005 |
113 |
ɸ value corresponding to the fixed glucose flux, obtained when the amplitude of perturbation A = 0. The rest of the values of LZ and the normalized ATP/ADP ratio correspond to pairs [f/r; A] belonging to each indicated region.
It was found that dynamics of period-k are obtained for high values of A and f/r (Figure 2). These dynamics have a mean complexity similar to the autonomous model (Table 3). However, when the values of the normalized ATP/ADP ratio were evaluated for regions II and III, the values found were higher than the corresponding ones to the autonomous model (Table 3). This could mean that an increase in the proliferative capacity of the tumor cells may occur. These results showed that it is not convenient to use periodic pulses as therapy in tumors that exhibit oscillating glycolysis.
Periodic glucose deprivation
Figure 3 shows the bifurcation diagram resulting from the perturbation of the model with periodic glucose deprivation. The qualitative behaviors exhibited are the same as those achieved with periodic pulses: period-k and quasiperiodicity (region I) and period-k (region II). The fundamental difference between the dynamic responses obtained by both forms of perturbation lies in the area that occupies the most complex region (darker zone) in the bifurcation diagrams. This area becomes smaller when the model is forced with periodic deprivation.
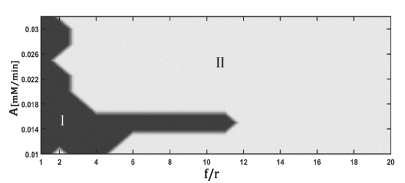
Figure 3. Representation of the kinetic model of glycolysis, adapted to HeLa tumor cells
A : Amplitude of perturbation; f/r: ratio between the frequency of perturbation and the minimum frequency used in the perturbation. Region I: period-k and quasiperiodicity; Region II: period-k. The dynamic responses were classified by stroboscopic analysis.
The robustness of the tumor only increases in a narrow domain of and f/r, bounded by small values of f/r (Figure 3: darker zone). Higher values of f/r led the system to a state where its mean complexity is similar to the autonomous model (Table 4: region II). It is notorious that the value of the normalized ATP/ADP ratio decreased in both regions with respect to the autonomous model (Table 4). Therefore, it would be convenient to periodically deprive the tumor cells of glucose using high values of perturbation frequency, since it could prevent the increase of the resistance capacity of the tumor cells and contribute to the decrease of its proliferative capacity. This strategy can increase the efficacy of antitumor therapies.
Table 4. Complexity and energy charge of the perturbed glycolytic model with periodic glucose deprivation
Region |
LZ |
Normalized ATP/ADP ratio (%) |
Autonomous model
(A = 0) |
0,003 ɸ |
100 ɸ |
| |
0,009 |
57 |
0,009 |
66 |
| |
0,006 |
71 |
0,002 |
3 |
ɸ value corresponding to the fixed glucose flux, obtained when the amplitude of the perturbation A = 0. The rest of the values of LZ and the normalized ATP/ADP ratio correspond to pairs [f/r; A] belonging to each indicated region.
Discussion
When the glucose input rate was varied, the updated model (autonomous model) simulated an oscillatory domain. This coincides with experimental findings reported in the literature [33,40]. Therefore, the modifications made to the previous model [15] were effective. Reliability in predictions made from periodic variations of the glucose input rate was guaranteed due to the existence of this oscillatory domain.
The molecular mechanism of autonomous oscillations in glycolysis was proposed by Goldbeter [33], according to the theory developed by Monod, Wyman and Changeux [24]. The mechanism proposes that high rates lead to a predominant relaxed state (R) in the enzyme PFK-1; while low rates lead to a predominant tense state (T). The predominance of T or R leads to a stable steady state; while the transitions (T-R) lead to sustained oscillations. These transitions occur at intermediate substrate input rates.
The application of periodic pulses of glucose caused quasiperiodic and period-k dynamics. These dynamics were found experimentally in cell-free extracts obtained from yeast that exhibited autonomous oscillations in the glycolytic mechanism, which were perturbed with periodic substrate input flux [20,21].
The results obtained show that the application of periodic pulses of glucose should be avoided from a therapeutic point of view. In contrast, a study conducted on human endothelial cells revealed that prolonged exposure to periodic pulses of external glucose leads to oxidative stress and cellular DNA damage. This can activate p53 tumor suppressor protein and trigger apoptosis [41]. However this is not a generality in tumors since there are allelic variants of the gene that encodes p53 that decrease the sensitivity of the tumor cell to apoptotic signals [42].
Predictions made from the application of periodic glucose deprivation agree with the results reported experimentally by Lee et al. [22], which showed that nutrient deprivation cycles affected the energy metabolism of different tumor cell lines, which was manifested through the arrest of the proliferative capacity of them. In vivo studies have shown that low blood glucose concentrations can increase the cytotoxicity of chemotherapeutic compounds [22,43]. This supports the possible effectiveness of the proposed strategy.
Mutations and epigenetic modifications that increase growth and promote insensitivity to anti-growth signals in cancer cells, lead to the loss of appropriate responses to rapidly adapt to a variety of extreme environments including starvation [22]. Recently a study based on a kinetic model of tumor glycolysis adjusted to steady state, showed that the application of intermittent fasting decreased the entropy production rate of glycolysis. In this study, the entropy production rate is considered as an indicator of robustness [44].
An important aspect to keep in mind is that therapies aimed at damaging glucose metabolism may fail due to the heterogeneity and the evolutive capacity of tumor cells [45]. It has been shown that some cancer cells have acquired a strong tolerance to stress [46], like the one induced by nutrient deprivation. Therefore, in order to improve the effectiveness of this strategy to a wide variety of tumors, it is recommended avoid the stress tolerance. The use of certain drugs has given good results in this regard [46,47].
Conclusion
Our results show how the environmental constraints, represented in this case by the availability of glucose, can affect the robustness and energy charge of neoplastic cells that exhibit oscillating glycolysis. The tumor microenvironment plays an important role in the fate of tumor cells [48]. Therefore, the design of chronotherapies that adequately alter the cancer environment can promote current therapies against it.
In summary, in this study we found:
Sustained increases in glucose influx causes a decrease in the robustness, but causes an increase in the cellular energy charge of tumor cells that exhibit an oscillating glycolysis.
Periodic glucose pulses performed at frequencies close to the autonomous frequency of oscillation of glycolysis can lead to an increase in the energy charge of tumor cells, so it should be avoided from a therapeutic point of view.
Periodically depriving the tumor microenvironment of glucose at high perturbation frequencies, regardless of the amplitude of perturbation, prevent the increase of robustness and cause a decrease in the cellular energy charge. This strategy can increase the efficacy of antitumor therapies.
Acknowledgments
Prof. Dr. A. Alzola in memoriam. We would like to thank Prof. Dr. Jacques Rieumont for support and encouragement for this research. One of the authors (JMNV) thanked the Institute of Physics of the UNAM Mexico for its warm hospitality.
References
- WARBURG O (1956) On the origin of cancer cells. Science 123: 309-314. [Crossref]
- Hanahan D, Weinberg RA (2011) Hallmarks of cancer: the next generation. Cell 144: 646-674. [Crossref]
- Marín-Hernández A, López-Ramírez SY, Del Mazo-Monsalvo I, Gallardo-Pérez JC, Rodríguez-Enríquez S, et al. (2014) Modeling cancer glycolysis under hypoglycemia, and the role played by the differential expression of glycolytic isoforms. FEBS J 281: 3325-3345. [Crossref]
- Marín-Hernández A1, Gallardo-Pérez JC, Ralph SJ, Rodríguez-Enríquez S, Moreno-Sánchez R (2009) HIF-1a modulates energy metabolism in cancer cells by inducing over-expression of specific glycolytic isoforms. Mini Rev Med Chem 9: 1084-1101. [Crossref]
- Elstrom RL, Bauer DE, Buzzai M, Karnauskas R, Harris MH, et al. (2004) Akt stimulates aerobic glycolysis in cancer cells. Cancer Res 64: 3892-3899. [Crossref]
- Gonzales-Rengifo GF, Gonzales-Castañeda C, Espinosa-Guerinoni D, Rojas-Tubeh C (2007) Sobre expresión de genes de las enzimas de la vía glicolítica en células cancerígenas. Acta Médica Peruana 24: 187-197.
- Ibsen KH, Schiller KW (1967) Oscillations of nucleotides and glycolytic intermediates in aerobic suspensions of Ehrlich ascites tumor cells. Biochim Biophy Acta 131: 405-407. [Crossref]
- Fru LC, Adamson EB, Campos DD, Fain SB, Jacques SL, et al. (2015) Potential role of the glycolytic oscillator in acute hypoxia in tumors. Phys Med Biol 60: 9215. [Crossref]
- Amemiya T, Shibata K, Itoh Y, Itoh K, Watanabe M, et al. (2017) Primordial oscillations in life: Direct observation of glycolytic oscillations in individual HeLa cervical cancer cells. Chaos 27: 104602. [Crossref]
- Montero F, Morán, F (1992) Biofísica: Procesos de autoorganización en Biología.
- Montero S, Durán I, Pomuceno-Orduñez JP, Martin RR, Mesa MD, et al. (2017) How much damage can make the glucose in cancer. J Tumor Res 3: 116.
- Xu RH, Pelicano H, Zhou Y, Carew JS, Feng L, et al. (2005) Inhibition of glycolysis in cancer cells: a novel strategy to overcome drug resistance associated with mitochondrial respiratory defect and hypoxia. Cancer Res 65: 613-621. [Crossref]
- Nieto-Villar JM, Izquierdo-Kulich E, Betancourt-Mar JA, Tejera E (2013) Complejidad y auto-organización de patrones naturales. Editorial UH, La Habana, Cuba, 2013.
- Kitano H (2007) Towards a theory of biological robustness. Mol Syst Biol 3: 137. [Crossref]
- Martin RR, Montero S, Silva E, Bizzarri M, Cocho G, et al. (2017) Phase transitions in tumor growth: V what can be expected from cancer glycolytic oscillations? Physica A: Statistical Mechanics and its Applications 486: 762-771.
- Hess B, Boiteux A (1968) Mechanism of Glycolytic Oscillation in Yeast, I. Aerobic and anaerobic growth conditions for obtaining glycolytic oscillation. Hoppe-Seyler´ s Zeitschrift für physiologische Chemie 349: 1567-1574.
- Demir H, Ciftci M, Kufrevioglu OI (2003) Purification of 6-phosphogluconate dehydrogenase from parsley (Petroselinum hortense) leaves and investigation of some kinetic properties. Prep Biochem Biotechnol 33: 39-52. [Crossref]
- Durrington HJ, Farrow SN, Loudon AS, Ray DW (2014) The circadian clock and asthma. Thorax 69: 90-92. [Crossref]
- Litinski M, Scheer FA, Shea SA (2009) Influence of the circadian system on disease severity. Sleep Med Clin 4: 143-163. [Crossref]
- Markus M, Kuschmitz D, Hess B (1984) Chaotic dynamics in yeast glycolysis under periodic substrate input flux. FEBS letters 172: 235-238. [Crossref]
- Markus M, Müller SC, Hess B (1985) Observation of entrainment, quasiperiodicity and chaos in glycolyzing yeast extracts under periodic glucose input. Berichte der Bunsengesellschaft für physikalische Chemie 89: 651-654.
- Lee, C., Raffaghello, L., Brandhorst, S., Safdie, F.M., Bianchi, G., Martin-Montalvo, A., et al., (2012) Fasting cycles retard growth of tumors and sensitize a range of cancer cell types to chemotherapy. Sci Transl Med 4: 124ra27-124ra27. [Crossref]
- Goldbeter A, Dupont G (1990) Allosteric regulation, cooperativity, and biochemical oscillations. Biophysical Chemistry 37: 341-353.]
- MONOD J, WYMAN J, CHANGEUX JP (1965) On the Nature of Allosteric Transitions: A Plausible Model. J Mol Biol 12: 88-118. [Crossref]
- Dynnik V, Sel'kov E (1973) On the possibility of self-oscillations in the lower part of the glycolytic system. FEBS Letters 37: 342-346.
- Termonia, Y. & Ross, J., (1981) Oscillations and control features in glycolysis: numerical analysis of a comprehensive model. Proc Natl Acad Sci U S A 78: 2952-2956. [Crossref]
- Marín-Hernández A, Gallardo-Pérez JC, Rodríguez-Enríquez S, Encalada R, Moreno-Sánchez R, et al. (2011) Modeling cancer glycolysis. Biochim Biophys Acta 1807: 755-767. [Crossref]
- Richard P (2003) The rhythm of yeast. FEMS Microbiol Rev 27: 547-557. [Crossref]
- Moreno-Sánchez R, Marín-Hernández A, Gallardo-Pérez JC, Quezada H, Encalada R, et al. (2012) Phosphofructokinase type 1 kinetics, isoform expression, and gene polymorphisms in cancer cells. J Cell Biochem 113: 1692-1703. [Crossref]
- Richter, O., Betz, A., & Giersch, C., (1975) The response of oscillating glycolysis to perturbations in the NADH/NAD system: a comparison between experiments and a computer model. Biosystems 7: 137-146. [Crossref]
- Teusink B, Bakker BM, Westerhoff HV (1996) Control of frequency and amplitudes is shared by all enzymes in three models for yeast glycolytic oscillations. Biochimica et Biophysica Acta (BBA)-Bioenergetics 1275: 204-212.
- Parker TS, Chua L (2012) Practical numerical algorithms for chaotic systems. Springer Science & Business Media.
- Goldbeter A (1997) Biochemical oscillations and cellular rhythms: the molecular bases of periodic and chaotic behaviour. 1997: Cambridge University Press.
- Silva E, Martin RR, Pomuceno-Orduñez JP, Mansilla R, Betancourt-Mar JA, et al. (2018) Dose and frequency in cancer therapy. Theoretical non-autonomous model of p53 network. Biological Rhythm Research: 1-7.
- Jaime JC, Mesa-Álvarez MD, Martin RR, Betancourt-Mar JA, Cocho G, et al. (2018) Chronotherapy of cancer: periodic perturbations in vascular growth and metastasis. Biological Rhythm Research: 1-10.
- Hoops S, Sahle S, Gauges R, Lee C, Pahle J, et al. (2006) COPASI--a COmplex PAthway SImulator. Bioinformatics 22: 3067-3074. [Crossref]
- Lempel A, Ziv J (1976) On the complexity of finite sequences. IEEE Transactions on information theory 22: 75-81.
- Takens F (1981) Detecting strange attractors in turbulence, in Dynamical systems and turbulence, Warwick 1980: 366-381.
- Hu J, Gao J, Principe JC (2006) Analysis of biomedical signals by the lempel-Ziv complexity: the effect of finite data size. IEEE Trans Biomed Eng 53: 2606-2609. [Crossref]
- Goldbeter A (2017) Dissipative structures and biological rhythms. Chaos: An Interdisciplinary Journal of Nonlinear Science 27: 104612. [Crossref]
- Schisano B1, Tripathi G, McGee K, McTernan PG, Ceriello A (2011) Glucose oscillations, more than constant high glucose, induce p53 activation and a metabolic memory in human endothelial cells. Diabetologia 54: 1219-1226. [Crossref]
- Sigal A, Rotter V (2000) Oncogenic mutations of the p53 tumor suppressor: the demons of the guardian of the genome. Cancer Res 60: 6788-6793. [Crossref]
- Zhuang Y, Chan DK, Haugrud AB, Miskimins WK (2014) Mechanisms by which low glucose enhances the cytotoxicity of metformin to cancer cells both in vitro and in vivo. PLoS One 9: e108444. [Crossref]
- Durán I, Pomuceno-Orduñez J, Martin R, Silva E, Montero S, et al. (2018) Glucose starvation as cancer treatment: Thermodynamic point of view. Integr Cancer Sci Therap 5: 1-5.
- Gatenby RA, Gillies RJ (2007) Glycolysis in cancer: a potential target for therapy. Int J Biochem Cell Biol 39: 1358-1366. [Crossref]
- Izuishi K, Kato K, Ogura T, Kinoshita T, Esumi H (2000) Remarkable tolerance of tumor cells to nutrient deprivation: possible new biochemical target for cancer therapy. Cancer Res 60: 6201-6207. [Crossref]
- Saito S, Furuno A, Sakurai J, Sakamoto A, Park HR, et al. (2009) Chemical genomics identifies the unfolded protein response as a target for selective cancer cell killing during glucose deprivation. Cancer Res 69: 4225-4234. [Crossref]
- D'Anselmi F, Masiello MG, Cucina A, Proietti S, Dinicola S, et al. (2013) Microenvironment promotes tumor cell reprogramming in human breast cancer cell lines. PLoS One 8: e83770. [Crossref]


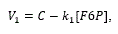
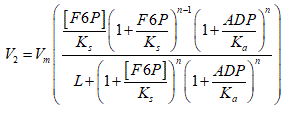
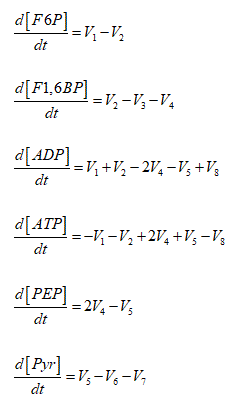
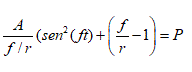 (2.2)
(2.2)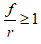 . Three cases can be analyzed:
. Three cases can be analyzed: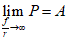 . In this case, the minimum rate of glucose influx tends to the maximum rate and a constant glucose influx is established. This flux is greater than the basal rate of glucose input. Physically, the constancy in this rate is due to the fact that a balance is reached between the rate of glucose influx in the tumor cell and the glucose consumption rate by non-tumor cells in the microenvironment. This prevents the sustained increase of glucose influx. When glucose is deprived with an infinite frequency, the constancy in the flux is due to a balance between the rate of glucose influx in the tumor cell and the rate with which the organism is able to reestablish its levels. In this case, the flux is lower than the basal rate of glucose input. This prevents the sustained decrease of glucose influx.
. In this case, the minimum rate of glucose influx tends to the maximum rate and a constant glucose influx is established. This flux is greater than the basal rate of glucose input. Physically, the constancy in this rate is due to the fact that a balance is reached between the rate of glucose influx in the tumor cell and the glucose consumption rate by non-tumor cells in the microenvironment. This prevents the sustained increase of glucose influx. When glucose is deprived with an infinite frequency, the constancy in the flux is due to a balance between the rate of glucose influx in the tumor cell and the rate with which the organism is able to reestablish its levels. In this case, the flux is lower than the basal rate of glucose input. This prevents the sustained decrease of glucose influx.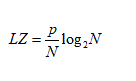 (2.3)
(2.3)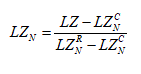 (2.4)
(2.4)
