Take a look at the Recent articles

Abstract

It is proved that if a smooth function 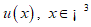, such that 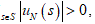where U_N is the normal derivative of u on S, has a closed smooth surface S of zeros, then the function  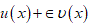has also a closed smooth surface S_e  of zeros. Here u is a smooth function and  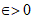is a sufficiently small number.

Key words

zero surfaces, perturbation theory

Introduction

Let 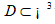be a bounded domain containing inside a connected closed C³-smooth surface S, which is the set of zeros of a function 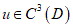, so that Consider the scattering problem:

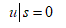                                (1)

Let N = N_s be the unit normal to S, such that 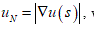where U_N is the normal derivative of u on S. Let 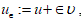, where 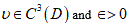is sufficiently small. Assume that

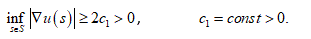                 (2)

The purpose of this paper is to prove Theorem 1.

Theorem 1. Under the above assumptions there exists a smooth closed surface S_e  such that U_e = 0 on S_e.

In Section 2 Theorem 1 is proved.

Although there are many various results on perturbation theory, see [2], [3], the result formulated in Theorem 1 is new.

Proof of Theorem 1

Consider the following equation for t:

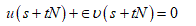                                     (3)

where N = N(s) is the normal to S at the point s and t is a parameter. Using the Taylor's formula and relation (1), one gets from (3)

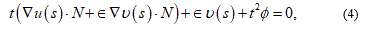
where 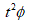 is the Lagrange remainder in the Taylor's formula and

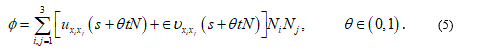
Since the functions u and 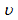 belong to C³(D), the function 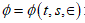has a bounded derivative with respect to t uniformly with respect to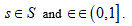

Consider equation (4) as an equation for t = t(s) in the space C(S). Rewrite (4) as

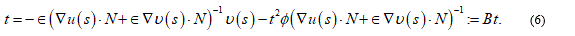
Let us check that the operator B satisfies the contraction mapping theorem in the set

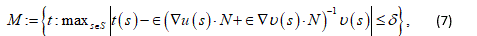
where 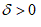 is a small number, and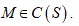

First, one should check that B maps M into itself. One has

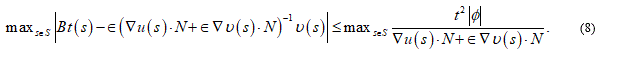
We have chosen N so that 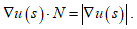This is possible because equation (1) implies that 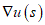is orthogonal to S at the point 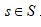Assumption (2) implies that for sufficiently small ∈ one has

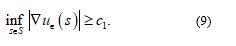
Since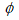is continuously differentiable, one has

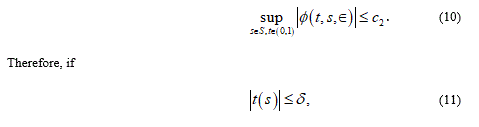
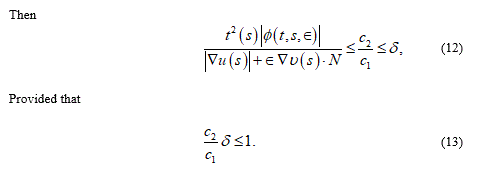
Thus, if (13) holds then B maps M into itself.

Let us check that B is a contraction mapping on M. One has

is sufficiently small. Indeed,

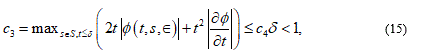
if δ is suciently small. Here C₄  is a constant.

Thus, B is a contraction on M. By the contraction mapping principle, equation (6) is uniquely solvable for t. Its solution t = t(s) allows one to construct the zero surface S_e of the function U_e by the equation r = s + t (s) N , where r = r (s) is the radius vector of the points on S_e.

Theorem 1 is proved.

Remark 1. Condition (2) is a sufficient condition for the validity of Theorem 1. Although this condition is not necessary, if it does not hold one can construct counterexamples to the conclusion of Theorem 1. For example, assume that
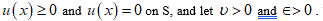Then the function  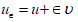does not have zeros in i ³.

Remark 2. In scattering theory the following question is of interest: assume that u (x) is an entire function of exponential type, 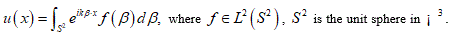Assume that u = 0 on S, where S  is a closed smooth connected surface in i ³.

Is there another closed smooth connected surface of zeros of an entire function U_e of exponential type,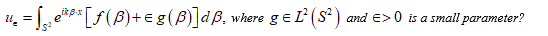

We will not use Theorem 1 since assumption (2) may not hold, but sketch an argument, based on the fact that S in the above question is the intersection of an analytic set with i ³, see, for example, [1] for the definition and properties of analytic sets. The functions u and u_e in Remark 2 solve the differential equation

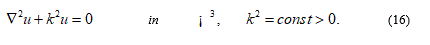
The function u_N  may vanish on S at most on the closed set 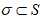which is of the surface measure zero (by the uniqueness of the solution to the Cauchy problem for equation (16)). For every point  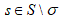the argument given in the proof of Theorem 1 yields the existence of t(s), the unique solution to (6). Since S is real analytic the set S_e , defined in the proof of Theorem 1, is analytic and is a part of the analytic set defined by the equation u_e = 0. In our problem S is a bounded closed real analytic surface. The set S_e can be continued analytically to an analytic set which intersects the real space i ³  over a real analytic surface S_e. It is still an open problem to prove (or disprove) that the analytic continuation of the set S_e intersects i ³  over a bounded closed real analytic surface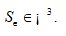

References

1. Fuks B (1963) Theory of analytic functions of several complex variables, AMS, Providence RI.
2. Kato T (1984) Perturbation theory for linear operators, Springer Verlag, New York.
3. Ramm AG (2005) Inverse problems, Springer, New York.