Take a look at the Recent articles

Abstract

Background: Bayesian adaptive designs have the potential to change the way clinical research is conducted. These novel study designs can answer the same questions as traditional efficacy trials but with potential advantages in terms of flexibility and efficiency.  The Bayesian adaptive drop-the-loser (DTL) design is particularly applicable in trials where there are uncertainties regarding which treatment/dose level to test further. 

Aims: This paper describes steps taken in planning an ongoing DTL randomized clinical trial of citalopram for the treatment of cocaine use disorder, including the design rationale, simulation study, and pruning criteria. 

Method and results:  Participants of this single site, double-blind, randomized controlled trial are assigned to either citalopram 20 mg/day, 40 mg/day, or placebo for 9 weeks.  The primary outcome measure is longest duration of abstinence (LDA) based on urine drug screens. A planned interim analysis at 50% of data gathering will drop or “prune” the active medication group that is performing least well, based on pre-specified decision rules. Bayesian simulation results show that this adaptive design allocates more subjects to the ‘best efficacy’ dose condition with satisfactory power and Type I error rates. 

Discussion: Employing the proposed DTL design is likely to yield the same conclusions as the classical fixed (non-adaptive) design, but with greater statistical precision for estimating treatment effects.  We discuss advantages of DTL for speeding up efforts underway to identify and test new medications to treat cocaine dependence. We also discuss logistical considerations and lessons learned from designing and implementing this trial.

Key words

bayesian adaptive design, drop-the-loser, citalopram, cocaine

Introduction

Cocaine use disorder (CUD) is a difficult to treat medical and public health problem.  Research on the development of effective treatment medications has been a high priority but has not resulted in high success rates.  Randomized clinical trials have evaluated over 60 medications, however none have FDA-approval for the treatment of cocaine dependence, leaving the field in need of more efficient ways to move forward with the most promising candidate drugs and doses [1]. Adaptive trial designs have accelerated the drug development process for lung cancer, breast cancer, stroke, and diabetes [2-5] and could potentially do the same for the drug dependence field. We developed a drop-the-loser (DTL) Bayesian adaptive design to study the dose-response relationship of the selective serotonin reuptake inhibitor (SSRI) citalopram in the treatment of CUD.  Here we describe the key steps taken to design this study and the advantages it could potentially have for future medication development efforts for the treatment of cocaine and other substance use disorders.

Pharmacological rationale

Data from human and animal studies have demonstrated neuroadaptations that are correlated with, or caused by, chronic stimulant use.  In addition to long-term changes in dopaminergic systems, alterations in serotonin (5-hydroxytryptamine (5-HT)) transmission have also been reported in addicted individuals.  Specifically, depletion of brain 5-HT has been associated with the compulsive behavior seen in CUD [6-9]. The therapeutic potential of reversing this deficit with serotonergic medications has received attention in clinical trials of SSRI agents for CUD.  Relative to other SSRI’s that have produced largely negative results in cocaine clinical trials [10-14], citalopram, a highly selective serotonin reuptake inhibitor with high affinity for the 5-HT transporter, has been effective in reducing cocaine-positive urines when administered with behavioral therapy in a double-blind placebo-controlled trial [15]. To date, the highest dose of citalopram evaluated in a randomized clinical trial (RCT) for the treatment of CUD has been 20 mg/day; substantially lower than doses shown to be beneficial for the treatment of obsessive compulsive disorder (i.e., 60 mg/day).  Uncertainty regarding the adequate dose of citalopram for treatment of CUD prompted us to design a double-blind trial comparing two active medication arms (20 mg/day; 40 mg/day) with placebo.  The primary aim of the study is to select the most promising treatment arm to evaluate in a subsequent larger confirmatory trial, thus, we selected a DTL study design based on the following rationale. 

Design rationale

Drawbacks of traditional clinical trials: Most medication development trials, including those in the field of substance use disorders, have employed conventional, placebo-controlled, fixed parallel group designs, involving only a few dose conditions and large sample sizes. These trials have been criticized for being too long, too expensive, and often uninformative if initial dose selection proved to be incorrect [16].  Two ways in which the clinical trial enterprise may be enhanced are the implementation of adaptive clinical trial designs and the application of Bayesian statistical approaches in monitoring and analyzing clinical trials [17-19].

Adaptive designs: Adaptive designs permit critical mid-trial design modifications to be made, based on interim information [16].  Since adaptations to the trial are pre-specified (by design) and not made in an unplanned or ad hoc manner, the integrity and validity of the trial are preserved.  These adaptations are aimed at providing (1) better treatment of patients by limiting exposure to nonefficacious or unsafe doses and increasing exposure to more efficacious doses; (2) more efficient drug development; and (3) better use of available resources [20,21].

A drop-the-loser (DTL) adaptive design is useful in phase II clinical development especially when there are uncertainties regarding the dose levels [21-24].  DTL designs allow for multiple treatment arms with the opportunity to more fully characterize the dose-response curve during the initial phase of the trial. An interim analysis plan specifies the criteria for dropping doses that fail to show clinically meaningful efficacy over placebo. Conditions satisfying interim efficacy criteria are continued to completion.  All dose groups, dropped or continued, contain valuable information for final statistical analysis regarding dose response of the treatment under study.  This adaptive pruning permits the randomization of remaining participants to the conditions which demonstrate the most encouraging performance.

Bayesian statistical approaches: The recommended analysis strategy when using adaptive trials is Bayesian [17]. Put simply, the Bayesian strategy permits statements about the probability that treatment confers benefit.

Bayesian analysis posits a data generation model governed by an unknown model parameter, and often has as its goal the estimation of this parameter. Since there is uncertainty around the value of the parameter, the parameter is modeled as a probability distribution. Existing information about the parameter is represented by a prior probability distribution P(θ) that quantifies prior information about different parameter values that are obtained. Observed data from the current trial is represented by the likelihood P(data|θ) which is a probability distribution that quantifies how well the parameter values support the data. These two sources of evidence about the unknown parameter are mathematically combined to yield the posterior probability distribution using Bayes’ theorem:

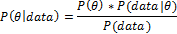
The posterior distribution permits direct statements about the probability of a given effect size given the observed data (i.e.,  P(θ|data)). Bayes’ Theorem provides a mathematical learning rule that prescribes the optimal way to update prior evidence for parameter values with observed data [25].  As treatment outcomes accumulate over the course of the trial, updated posterior distributions provide increasingly precise estimates of treatment effects.  Moreover, the probability that effects equal or exceed pre-specified threshold values can inform planned trial adaptations that may include altered allocation ratios for future randomization of subjects.

In situations like the current trial where there is little outside information about the optimal dose, a diffuse prior is often specified that is essentially flat across the range of possible parameter values. In such cases, the prior may not be reasonable from the clinicians’ perspective (i.e., implying that the treatment effect is equally likely to be beneficial and harmful) [26] but the posterior distribution it generates based on observed data is reasonable [17].

Prior specification: In the context of clinical trials, the prior distribution represents information about the parameter of interest in the absence of the observed outcomes. As with all statistical modeling, the choice of prior is a compromise between mathematical tractability, computational feasibility, and plausibility [27]. There are two distinct types of prior probability distributions to be considered.  This distinction becomes important in planning Bayesian adaptive designs: use of clinical trial simulation for trial design requires rapid computation for feasibility while analysis of the data may ultimately employ more computationally intensive, but statistically flexible methods. More flexible methods may be necessary in the final analysis if, for instance, data violate parametric assumptions (e.g. in the original citalopram study [15] the outcome met Poisson assumptions, failure to do so in the current trial may require specification of negative binomial or zero-inflated distributions which might require more computationally intensive strategies such as Markov chain Monte-Carlo (MCMC) approaches). Conjugate prior distributions are attractive because they produce a posterior distribution of the same family as the prior, and simple formulas can quickly generate the posterior from the prior and likelihood. The mathematical and computational ease of using conjugate prior distributions is offset by their inflexibility. The Gamma distribution is the only conjugate prior for the Poisson likelihood, but the Gamma distribution may not be a plausible representation of the prior information about the parameter θ.

For a given likelihood, a non-conjugate prior is any probability distribution that is not conjugate to that likelihood. Since any probability distribution can be used, non-conjugate priors are extremely flexible. However, there is generally no closed-form solution for generating the posterior distribution from a non-conjugate prior. In the absence of closed-form solutions, MCMC methods, like the Metropolis-Hastings algorithm, are used to produce random samples from the posterior. The empirical distribution composed of many MCMC samples permits inference on the posterior distribution, though generating a sufficient number of samples for accurate inference takes significant computational time relative to computing the posterior from a conjugate prior.

Method

Study design, participants, setting

The current study is a double-blind, placebo-controlled randomized clinical trial with participants assigned to one of three possible medication conditions (citalopram 20 mg, citalopram 40 mg, placebo).  Adult patients with CUD responding to study recruitment advertisements undergo an intake evaluation to determine potential eligibility.   Inclusion criteria for the trial require being between 18 and 60 years old and meeting Diagnostic and Statistical Manual of Mental Disorders-IV (DSM-IV) criteria for current cocaine dependence with provision of at least one benzoylecgonine (BE)-positive urine prior to randomization.  Exclusion criteria include:  (1) dependence on alcohol or drugs other than cannabis or nicotine; (2) current non-substance induced Axis I psychotic, depressive, or anxiety disorder; (3) presence of existing cardiovascular disease including cardiac conduction defects as determined by electrocardiogram (EKG) evaluated by the collaborating cardiologist, and/or symptoms suggestive of cardiovascular problems not related to drug use such as hypertension (treated or untreated), stroke, chest pain; (4) taking medications that would contraindicate study medications (e.g., MAO inhibitors, other SSRI’s); (5) pregnancy or nursing; and (6) court-mandated treatment for cocaine dependence.   A total sample of 125 participants will be enrolled in this single-site trial taking place at the outpatient Treatment Research Clinic (TRC) located at the University of Texas Houston, Center for Neurobehavioral Research on Addiction (CNRA). The research protocol, consent form, and all assessment/advertising materials are approved by the Committee for the Protection of Human Subjects (CPHS) of the University of Texas Medical School, Houston (Clinicaltrials.gov Identifier: NCT01535573).

Study procedures

Following assignment to one of the treatment groups, participants attend thrice weekly (MWF) clinic visits, including once a week individual cognitive-behavioral psychotherapy. Study medication is dispensed at each clinic visit along with a prize-bowl contingency management intervention reinforcing attendance [28].  Medication treatment begins with a 1-week dose escalation schedule, followed by maintenance for 7 weeks, and a 1-week dose reduction at week 9.

Study assessments

During intake evaluation, all subjects undergo a medical history and physical examination, laboratory tests (liver and thyroid function), and cardiac evaluation (i.e., 12- lead electrocardiogram). Vital signs (including heart rate, blood pressure, and weight) are obtained weekly during treatment. EKGs and blood pressure are closely monitored throughout the study, with a requirement of being normotensive (< 140/90) to receive study medications. The Structured Clinical Interview for DSM-IV [29] and Addiction Severity Index [30] are administered to assess diagnostic criteria and addiction severity.  A side-effects checklist is completed each week, with moderate to severely rated items evaluated by the study nurse and reviewed by the study physician. Cocaine use is assessed via urine rapid tests with Abuscreen OnTrak immunoassay kits (Roche Diagnostic Systems, Somerville, NJ) detecting the presence of cocaine (BE values > 300 ng/ml considered positive). Self-report data on cocaine use is collected at each clinic visit using a timeline follow-back procedure.  The primary outcome measure is longest duration of abstinence (LDA) based on urine BE values < 300 ng/ml.  As used in the initial citalopram trial [15], LDA is a count variable which follows a Poisson distribution.  It serves as a composite metric of both treatment retention and cocaine use [31].

Adaptation and analytic plan

Initial randomization and interim analysis plan: The first 63 subjects enrolled (50% of total sample size) are urn randomized to placebo, 20 mg/d of citalopram, or 40 mg/d of citalopram to ensure balanced groups with respect to severity of cocaine addiction [32].  A planned interim analysis will be performed at 50% of data gathering (n=63) to drop or “prune” the active medication group that is performing least well.  This analysis will be based on the primary endpoint, LDA.  Interim decision rules for pruning based on simulation results (described below) are shown in Figure 1.  An unblinded, third-party statistician will perform the analysis and report the results to the pharmacist, keeping the investigators and staff blind until the second half of the trial is over (Figure 1).

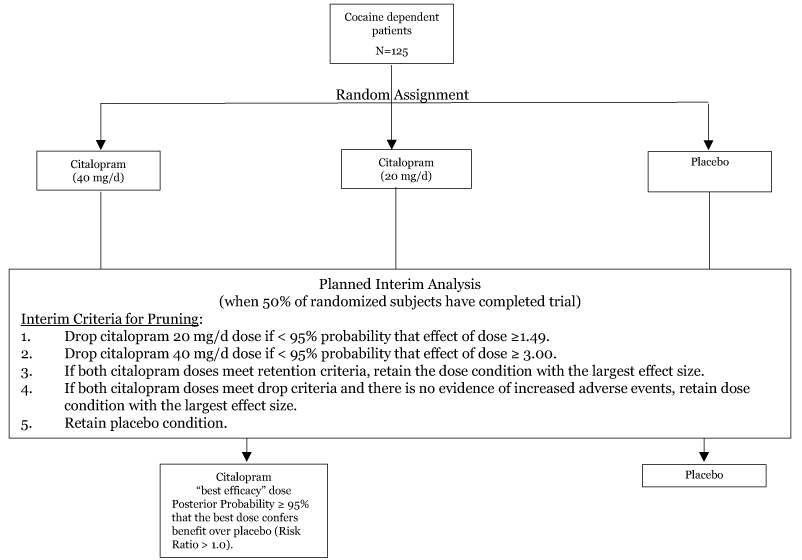
Figure 1. Diagram of the adaptive DTL clinical trial design of citalopram for CUD showing randomization to three initial treatment arms. Based on the findings of the interim analysis, the treatment arm that is performing least well will be dropped based on pre-specified criteria. The “best efficacy” arm, defined here as the condition showing a 95% probability of benefit over placebo (Risk Ratio > 1.0) will proceed to the second half of the trial.

Statistical model: Interim and final analyses utilize Bayesian generalized linear models for count outcomes. Several potential models exist for count data (e.g. Poisson, Negative Binomial, etc.), so model selection is dependent on goodness-of-fit, indexed by the Deviance Information Criterion [25]. The Deviance Information Criterion (DIC) is a generalization of the Akaike Information Criterion and Bayesian Information Criterion. Similar to these other penalized likelihood criteria, the DIC measures relative goodness-of-fit adjusting for model complexity, with smaller values indicating better fit to the observed data. The prior distributions are specified as vague and neutral: beta regression coefficients ~ N (mean=0, variance = 1 × 10⁶) in the log form, and ~Unif (0,1) for the inverse of the dispersion parameter (for models other than the Poisson). This extremely vague and neutral prior allows the observed data to dominate the effect size estimates.

Decision rules: Anticipated effects are based on results from Moeller, et al. [15].  Pre-specified decision rules using the Bayesian posterior probabilities at the interim analysis will dictate which doses to retain for the remainder of the trial. The placebo condition is always retained. If there is < 95% posterior probability that the 20mg dose increases LDA by a factor of 1.49 relative to placebo, then the 20mg treatment arm will be dropped. If there is a < 95% posterior probability that the 40mg dose increases LDA by a factor of 3.0 relative to placebo, then the 40mg treatment arm will be dropped. If both conditions meet the retention criteria, then the condition with the largest effect size will be retained. If both conditions meet the drop criteria, then the condition with the largest effect size will retained, unless there is evidence of increased adverse effects. The final 62 subjects to enroll in the trial will be urn randomized to placebo or the retained, ‘best efficacy’ citalopram condition.

Final analysis: The final analysis will include all patients, evaluating LDA as a function of treatment: those from the placebo treatment arm (N = 52), the retained treatment arm (N = 52), and the treatment arm that was pruned at the interim analysis (N = 21). Though the pruned treatment condition will have a smaller sample size, the observed patients still provide information about efficacy of that dose, albeit with less precision than available for the retained treatment arm.  The design stipulates that, at the final analysis, 95% posterior probability of a difference between an active condition and placebo constitutes sufficient evidence to conclude that a statistically reliable difference exists.  Final results from this ongoing trial will be reported in a forthcoming publication.

Simulation study

Designing an adaptive trial typically begins with a simulation study to address issues such as timing and frequency of interim analyses, and to understand the operating characteristics associated with the criteria for dropping arms.  A Monte Carlo simulation study assessed the merits of a DTL design relative to a non-adaptive parallel-group approach.  The simulation study evaluated multiple decision rules under three different scenarios that may occur during the trial. Though many decision rules were evaluated, only simulation results for the proposed decision rules are reported. The 2007 finding by Moeller, et al. [15] that 20 mg citalopram increased LDA by a factor of 2.5 relative to placebo guided the choice of simulated effect sizes.

Allocation of existing resources for conducting the clinical trial placed limitations on the sample size we could credibly randomize (N = 125).  As mentioned, substantial evidence already existed for the anticipated effects in the placebo and 20 mg citalopram conditions [15] and expert opinion permitted credible estimates for the 40-mg condition.  Having defined the sample size and anticipated effects we simulated K = 10,000 clinical trials testing the performance of various decision-rules for the correct selection of the best dose (in this case 40 mg citalopram).  The simulations evaluated multiple decision rules that manipulated two parameters, the effect size that constituted a clinically meaningful value, and the posterior probability that this effect existed.  Having identified a set of effect sizes and posterior probabilities that, by consensus we agreed would constitute sufficient evidence to warrant moving to a larger trial, we applied these rules to additional scenarios. 

Scenario One considered a dose-related efficacy increase, such that 40 mg of citalopram outperforms 20 mg of citalopram relative to placebo. This scenario was modeled as a 20 mg citalopram condition that increased LDA by a factor of 2.5 relative to placebo, and a 40mg citalopram condition that further increased LDA by a factor of 3.5 relative to placebo. The anticipated outcome in this scenario was retention of the 40 mg citalopram dose at the interim analysis, thereby exposing more patients to optimal treatment, and selection of the 40 mg citalopram dose as the optimal treatment at the final analysis. The proportion of simulated trials that identified the 40mg dose as optimal provided a Monte Carlo estimate of the power under this scenario.

Scenario Two considered the potential side effect profiles of the higher dose resulting in poorer performance for 40 mg of citalopram. This scenario was modeled as a 20 mg citalopram condition that increased LDA by a factor of 2.5 relative to placebo, and a 40 mg citalopram condition that did not outperform placebo (risk ratio of 1.0). The anticipated outcome in this scenario was retention of the 20 mg citalopram dose at the interim analysis and selection of the 20 mg citalopram dose as the optimal treatment at the final analysis. The proportion of simulated trials that identified the 20mg dose as optimal provided a Monte Carlo estimate of the power under this scenario.

Scenario Three considered the null case that neither dose of citalopram confers greater benefit than placebo. This scenario was modeled with 20mg and 40mg conditions with risk ratios of 1.0 relative to placebo. The proportion of simulated trials that identified either of the citalopram doses as superior to placebo provided a Monte Carlo estimate of the type I error rate.

Results

K = 10,000 simulations were run for each scenario to provide estimates of the trial’s operating characteristics. The LDA endpoint was modeled as a Poisson (θ) outcome, with risk ratios 1.0, 2.5, and 3.5 corresponding to θ = 2, 5, and 7 respectively. For simulation purposes, a Gamma (α = 2, β = 0.776) distribution provided a vague and neutral prior distribution for the Poisson distributed outcome. The Gamma distribution is the conjugate prior to the Poisson likelihood, providing a straightforward algebraic solution for the posterior distribution that substantially decreased computational burden. Note that this is different from the Normal (0, 1 × 10⁶) prior chosen for the analysis. Since the Normal (0, 1 × 10⁶) prior is not conjugate to the Poisson likelihood, there is no simple closed-form solution, so a computationally-intensive MCMC algorithm has to be used to estimate the posteriors. Although this MCMC approach is not too burdensome when analyzing the results of a single trial, evaluating the operating characteristics of a set of decision rules requires computing posteriors for 10,000 trials for each of three different scenarios. With the Gamma conjugate prior the full set of 30,000 trials takes minutes to simulate, but since the normal prior requires MCMC approximation, over an hour elapses before the results of the simulation are ready to be reviewed. Since the design phase of the trial requires simulating many thousands of simulations each for a spectrum of decision rules to identify the ones with desirable operating characteristics, the choice of the Gamma conjugate prior allows swift evaluation of the possible decision rules. Upon selection of decision rules, simulations using MCMC confirmed the desirable operating characteristics hold with a Normal (0, 1 × 10⁶) prior.

Simulation results, presented in Table 1, support the proposed DTL design in showing that under scenarios reflecting the hypothesized treatment effects, the adaptive design allocates more subjects to the more promising treatment conditions, i.e., appropriate “pruning” of less efficacious conditions. Under Scenario One, the simulations demonstrated this trial design has 90.2% power (probability of selecting the 40 mg as optimal at the final analysis), and on average 49.99 subjects are allocated to the optimal dose. Under Scenario Two, the simulations demonstrated this trial design has 81.8% power (probability of selecting the 20 mg as optimal at the final analysis), and on average 52 subjects are allocated to the optimal dose. Under Scenario Three, this trial design has a less than 0.01% Type I error rate (probability of deciding that either dose is better than placebo). As mentioned, simulations in Table 1 utilized conjugate gamma priors for Poisson outcome which were computationally more efficient for evaluating a wide variety of decision rules. At the same time the use of the gamma prior did not reflect the final planned analysis approach, and was somewhat more informative than that planned approach (hence the observed lower Type 1 error rate).  As such we utilized the more computationally efficient approach to identify a subset of decision rules for evaluation using the final analytic model which was computationally more intense requiring MCMC methods.  Subsequent inspection of the rates using the vague, neutral Normal priors (Table 2) indicates satisfactory power and Type I Error rates.  These compare favorably with the classical fixed design which achieves similarly high power and low Type I error rate, but only allocates 42 subjects to the optimal treatment arm. Thus, employing the proposed DTL design is likely to yield the same conclusions as the classical fixed (non-adaptive) design, but with greater statistical precision for the most promising treatments (Table 1 and 2).

Table 1. Operating characteristics of proposed DTL design with Gamma prior. ^aSelection at the interim analysis uses the pruning criteria of > 0.95 posterior probability that effects are R.R. > 1.49 and 3.00 relative to placebo for Doses 20 mg and 40 mg respectively. ^bSelection at the final analysis uses the criteria of > 0.95 posterior probability that effects of the selected treatment confers benefit (R.R. > 0) relative to placebo.

Table 2. Operating characteristics of proposed DTL design with Normal prior. ^aSelection at the interim analysis uses the pruning criteria of > 0.95 posterior probability that effects are R.R. > 1.49 and 3.00 relative to placebo for Doses 20 mg and 40 mg respectively. ^bSelection at the final analysis uses the criteria of > 0.95 posterior probability that effects the selected treatment confers benefit (R.R. > 0) relative to placebo. 

The decision rules demonstrated adequate power and Type I error rates at interim analysis. Relative to a conventional parallel groups design, the sample size allocated to the placebo and most promising conditions increased by 20% and 23% respectively for Scenarios One and Two. This increase in sample size results in a corresponding increase in precision for the effect size estimate.

Discussion

Summary

Here we report the rationale and supporting documentation for a novel DTL adaptive clinical trial of citalopram for treatment of CUD.  Based on preliminary support for the SSRI citalopram, the present study seeks confirmation and determination of optimal dosing. The Moeller, et al. [15] effects were used to construct decision rules that were subsequently simulated and confirmed to have desirable operating characteristics.  In the end, the trial should demonstrate efficiency by reducing the sample size in the poorer performing condition and, in doing so, allocating resources to the most promising condition, thereby providing a more precise estimation of the treatment’s effect.  This innovative design is not without practical issues and considerations, outlined below.

Assumption of constant patient population

The many benefits of adaptive clinical trials require additional planning during the design of the trial. Adaptive trials assume that patient characteristics are constant over the entire duration of the trial [33]. If a population from which an investigator samples changes over time (e.g. a newly introduced, successful treatment alters the nature of the patients still seeking to enroll in an ongoing clinical trial), then the effect sizes from before and after the interim analysis may not be exchangeable.  It is incumbent on an investigator to appraise the likelihood that such a secular (exogenous) change might occur.  As it is often discussed, the investigator must evaluate the “treatment horizon” or the number of patients that will likely be treated according to currently prevailing practice [34].  In our case, the treatment horizon was likely to remain unchanged through the course of the trial:  no efficacious treatments currently exist for cocaine dependence and none under study are ready for FDA indication. This assumption can also be threatened by protocol amendments that change inclusion/exclusion criteria, leading to a trial adapting to a moving target population [21].  The present trial addresses this by carefully selecting inclusion/exclusion criteria consistent with those used at this center for over 20 years of clinical trials for cocaine dependence. Characteristics of participants recruited into studies at UT-Houston have, and are anticipated to, remain relatively constant through the course of the trial.

2021 Copyright OAT. All rights reserv

Enrollment rate and follow-up time

Useful adaptation depends on the tradeoffs between enrollment rate and follow-up time; if the enrollment rate is too high relative to the time required to obtain endpoints with delayed readout, all the patients may be enrolled before the interim analysis results are available [35]. In the present trial, the LDA endpoint is feasible despite delayed availability due to estimated enrollment rates at the study site.

Timely trial adaptation also requires swift electronic data capture and transmission to the data analysis group [33,36]. Clinical staff electronically entered urine drug screen results on the same day as testing and statistical staff frequently examined the database to check for data entry errors, so that a cleaned dataset would be promptly available for interim analysis.

Informed consent

Accurately conveying study information to participants during the informed consent process is straightforward. In this trial, since the medication is the same in both active treatment arms and clinic staff remain blind to condition assignment, the informed consent form does not discuss the adaptive nature of the trial. In other trials, statements such as “At first, there will be an equal chance of being assigned to either group. As the study goes along, however, the chance of being assigned to the treatment that worked better so far will increase” have been included on informed consent documents [37].

Deterministic retention rules

Given its proof-of-concept nature, this trial differs from an optimal adaptive design. In this trial, failure of both conditions to meet the probabilistic decision-rule thresholds resulted in the deterministic retention of the best condition. It is possible that the pre-specified probabilistic decision-rule thresholds could potentially be too strict, prematurely dropping treatment arms that confer benefit over placebo. This is evident by the type I error rate < 0.0001.  Based on our experience, rather than lowering the thresholds, we recommend using the distributions of anticipated effects to take into account uncertainty concerning the effect size parameter values. This would permit for more robust and realistic clinical trial planning.  Given the need to evaluate the adequacy of the decision-rules as well as salient secondary hypotheses, we decided to retain the best-performing active condition in the absence of harm.  A more efficient design might simply end the trial at the interim analysis if both active treatments failed to meet the thresholds.  

Similarly, if both active treatments met probabilistic decision-rule thresholds, then only the best condition was retained. Depending on the goal of the trial, both conditions might be retained to weigh the utility of both doses. However, the goal of this trial was to identify an optimal dose for a registration trial, so deterministic retention of only a single active treatment provides for more precise effect size estimates for that dose to better inform the confirmatory trial.

Interim analysis delay

In the current trial, after enrollment of the 63^rd subject, we plan to halt further enrollment and wait until all of the subjects in the initial phase complete the 13-week treatment, so that a complete dataset can be used for the interim analysis. Though the enrollment rates at the study site are modest, this temporary break in enrollment will slightly increase the overall time required to complete the trial. The alternative, i.e., to continue enrollment beyond the 63^rd participant prior to interim analysis, poses the chance that participants who are enrolled during the interim analysis delay might perform in such a way as to alter the conclusions of the interim analysis.  For instance, if just prior to the completion of the 63^rd participant, two additional participants were randomized to the condition that the interim analysis recommended dropping, and these participants, upon completion, behaved in such a way as to alter the interim analysis conclusions, investigators would face the question of whether the decision-rule had truly optimized the trial. One way to potentially avoid this halt to enrollment would be to conduct a sensitivity analysis utilizing a posterior-predictive distribution to assess the chance that the observations remaining to be made on active participants might change the interim analysis conclusions [38].  Assuming that the probability does not exceed some predefined cut-off, investigators could proceed with the trial with reasonable confidence that the interim analysis conclusions would not require revision.

Conclusions

Bayesian adaptive designs can increase efficiency of clinical trials. Increased precision of estimates for the most efficacious condition can result from allocation of a larger proportion of participants to the most salient conditions based on appropriate decision-rules. Monte Carlo simulation can be used to identify decision-rules that demonstrate accepted levels of Power and Type I Error associated with conventional parallel group clinical trials. Additional adaptive trial designs (e.g., Bayesian Continuous Re-Assessment Method for Phase I dose-finding) exist that can optimize other design characteristics.  These innovative design features have been underutilized in clinical trials of pharmacotherapies for drug addiction relative to other areas of medication development.  Given the urgent and unfulfilled need to identify an effective treatment medication of CUD, flexible designs that allow early detection of success or failure warrant serious consideration in future studies. 

Acknowledgments

Funding for this study was provided by the National Institute on Drug Abuse (NIDA) Medications Development Center Grant (P50-DA-9262).

References

1. Vocci F, Ling W (2005) Medications development: successes and challenges. Pharmacol Ther 108: 94-108. [Crossref]
2. Barker AD, Sigman CC, Kelloff GJ, Hylton NM, Berry DA et al. (2009) I-SPY 2: an adaptive breast cancer trial design in the setting of neoadjuvant chemotherapy. Clin Pharmacol Ther 86: 97-100.
3. Fiore LD, Brophy M, Ferguson RE, D'Avolio L, Hermos JA, et al. (2011) A point-of-care clinical trial comparing insulin administered using a sliding scale versus a weight-based regimen. Clin Trials 8: 183-195.
4. Kim ES, Herbst RS, Wistuba II, Lee JJ, Blumenschein, GR, et al. (2011) The BATTLE trial: personalizing therapy for lung cancer. Cancer Discov 1: 44-53.
5. Krams M, Lees KR, Hacke W, Grieve AP, Orgogozo JM, et al. (2003) Acute Stroke Therapy by Inhibition of Neutrophils (ASTIN): an adaptive dose-response study of UK-279,276 in acute ischemic stroke. Stroke 34: 2543-2548.
6. Ersche KD, Roiser JP, Robbins TW, Sahakian BJ (2008) Chronic cocaine but not chronic amphetamine use is associated with perseverative responding in humans. Psychopharmacology 197: 421-431.
7. Cunningham KA, Anastasio NC, Fox RG, Stutz SJ, Bubar MJ, et al. (2013) Synergism between a serotonin 5-HT2A receptor (5-HT2AR) antagonist and 5-HT2CR agonist suggests new pharmacotherapeutics for cocaine addiction. ACS Chem Neurosci 4: 110-121.
8. Fletcher PJ, Rizos Z, Noble K, Higgins GA (2011) Impulsive action induced by amphetamine, cocaine and MK801 is reduced by 5-HT(2C) receptor stimulation and 5-HT(2A) receptor blockade. Neuropharmacology 61: 468-477.
9. Winstanley CA, Theobald DE, Dalley JW, Glennon JC, Robbins TW (2004) 5-HT2A and 5-HT2C receptor antagonists have opposing effects on a measure of impulsivity: interactions with global 5-HT depletion. Psychopharmacology 176: 376-385.
10. Grabowski J, Rhoades H, Elk R, Schmitz J, Davis C, et al. (1995) Fluoxetine is ineffective for treatment of cocaine dependence or concurrent opiate and cocaine dependence: two placebo-controlled double-blind trials. J Clin Psychopharmacol 15: 163-174.
11. Schmitz JM, Averill P, Stotts AL, Moeller FG, Rhoades HM, et al. (2001) Fluoxetine treatment of cocaine-dependent patients with major depressive disorder. Drug Alcohol Depend 63: 207-214. [Crossref]
12. Winhusen TM, Somoza EC, Harrer JM, Mezinskis JP, Montgomery MA, et al. (2005) A placebo-controlled screening trial of tiagabine, sertraline and donepezil as cocaine dependence treatments. Addiction 100 Suppl 1: 68-77.
13. Mancino MJ, McGaugh J, Chopra MP, Guise JB, Cargile C, et al. (2014) Clinical efficacy of sertraline alone and augmented with gabapentin in recently abstinent cocaine-dependent patients with depressive symptoms. J Clin Psychopharmacol 34: 234-239.
14. Oliveto A, Poling J, Mancino MJ, Williams DK, Thostenson J, et al. (2012) Sertraline delays relapse in recently abstinent cocaine-dependent patients with depressive symptoms. Addiction 107: 131-41.
15. Moeller FG, Schmitz JM, Steinberg JL, Green CM, Reist C, et al. (2007) Citalopram combined with behavioral therapy reduces cocaine use: a double-blind, placebo-controlled trial. Am J Drug Alcohol Abuse 33: 367-378.
16. Gallo P, Chuang-Stein C, Dragalin V, Gaydos B, Krams M, et al. (2006) Adaptive designs in clinical drug development--an Executive Summary of the PhRMA Working Group. J Biopharm Stat 16: 275-283.
17. Berry DA (2006) Bayesian clinical trials. Nat Rev Drug Discov 5: 27-36. [Crossref]
18. Bauer P, Brannath W (2004) The advantages and disadvantages of adaptive designs for clinical trials. Drug Discov Today 9: 351-357. [Crossref]
19. West R (2016) Using Bayesian analysis for hypothesis testing in addiction science. Addiction 111: 3-4. [Crossref]
20. Pullman D, Wang X (2001) Adaptive designs, informed consent, and the ethics of research. Control Clin Trials 22: 203-210. [Crossref]
21. Chow SC, Chang M (2008) Adaptive design methods in clinical trials - a review. Orphanet J Rare Dis 3: 11. [Crossref]
22. Bauer P, Kieser M (1999) Combining different phases in the development of medical treatments within a single trial. Stat Med 18: 1833-1848. [Crossref]
23. Sampson AR, Sill MW (2005) Drop-the-losers design: normal case. Biom J 47: 257-268. [Crossref]
24. Li G, Wang Y, Ouyang SP (2009) Interim treatment selection in drug development. Stat Biosci 1: 268-288.
25. Spiegelhalter DJ, Best NG, Carlin BP, Linde A, Van der Klei, et al. (2002) Bayesian measures of model complexity and fit. Journal of Royal Statistical Society 64: 583-639.
26. Lan Gordon, KK, Hu P, Proschan MA (2009) A conditional power apporach to the evaluation of predictive power. Statistics in Biopharmaceutical Research 1: 131-136.
27. Gelman A, Shalizi CR (2013) Philosophy and the practice of Bayesian statistics. Br J Math Stat Psychol 66: 8-38.
28. Petry NM, Tedford J, Austin M, Nich C, Carroll KM, et al. (2004) Prize reinforcement contingency management for treating cocaine users: how low can we go, and with whom? Addiction 99: 349-360.
29. Spitzer RL, First MB (2005) Classification of psychiatric disorders. JAMA 294: 1898-1899. [Crossref]
30. McLellan AT, Kushner H, Metzger D, Peters R, Smith I, et al. (1992) The Fifth Edition of the Addiction Severity Index. J Subst Abuse Treat 9: 199-213. [Crossref]
31. Donovan DM, Bigelow GE, Brigham GS, Carroll KM, Cohen AJ, et al. (2012) Primary outcome indices in illicit drug dependence treatment research: systematic approach to selection and measurement of drug use end-points in clinical trials. Addiction 107: 694-708.
32. Stout RL, Wirtz PW, Carbonari JP, Del Boca FK (1994) Ensuring balanced distribution of prognostic factors in treatment outcome research. J Stud Alcohol Suppl12: 70-75.
33. Bornkamp B, Bretz F, Dmitrienko A, Enas G, Gaydos B, et al. (2007) Innovative approaches for designing and analyzing adaptive dose-ranging trials. J Biopharm Stat 17: 965-995.
34. Berry D (2004) Bayesian statistics and the efficiency and ethics of clinical trials. Statistical Science 19: 175-187.
35. FDA (2013) Guidance for Use of Bayesian Statistics in Medical Device Clinical Trials. Guidance for Industry and FDA Staff: U.S. Department of Health and Human Services. U.S. Food and Drug Administration.
36. Quinlan JA, Krams M (2006) Implementing adaptive designs: Logistical and operational considerations. Drug Information Journal 40: 437-444.
37. Biswas S, Liu DD, Lee JJ, Berry DA (2009) Bayesian clinical trials at the University of Texas M. D. Anderson Cancer Center. Clin Trials 6: 205-216. [Crossref]
38. Daimon T (2008) Predictive checking for Bayesian interim analyses in clinical trials. Contemp Clin Trials 29: 740-750. [Crossref]