The genetic code was studied hypothesizing that it has a mathematical underground like numerical schemes on the atomic level. A preceding article, including general arguments about this approach (http://dx.doi.org/10.1016/j.jtbi.2015.01.013), showed on the numeral series 5-0 with exponents 2/3 x100, the “ES-chain”, highly correlating with the distribution of atomic mass of 24 amino-acid side-chains. The weight-series of these, shortly noted, revealed a 3/2-division around the mean value, which led to this further analysis in elementary arithmetic.
The 3/2-relation marks also the divisions on C-skeleton and ‘substituents’ and on codon domains of uncharged amino-acids, indicating a deep interdependency.
The nucleon sums of the parts refer to the totals through transformations between number-base systems, strengthening the earlier hypothesis of such transformations as an internal reference system.
Main factors in the divisions of the total as ∼1500 appear as ‘Pythagorean’ squares. They are also found as intervals in the “ES-chain” as in the rings of complementary base-pairs and might represent a still more fundamental pattern.
Amino-acid side-chains grouped according to valences of “characterizing” atoms as along a different axis show in different pairings both the 3/2-division again and close congruence with two times the basic series as triplets 5-4-3 and 2-1-0.
Regularities in the spread of the weight-series are also noted and connections between amino-acids at its ‘center’ and the construction of purines and pyrimidines.
These and other findings reinforce the theory about numeral schemes behind the code, contradicting the ‘frozen accident’ hypothesis. Biological implications remain an open field for future studies.
numeral series, weight series of amino-acids, number-base transformation, pythagorean squares, valence groups, ile AUA
Abbreviations: aa(s): amino acid(s), R(-chains): side-chain(s) of amino acid(s), B(-chains): backbone chain(s) of amino acid(s), Mv: mean value, L-chain: amino acids lighter than Mv, H-chain: amino acids heavier than Mv
The construction of the genetic code and how to explain it has been the subject for an immense lot of studies for many decades. The theories are many. The error minimizing theory, the coevolution theory and the stereochemical theory, to mention a few, have been partly accepted, often objected to or at least problemized. No consensus has been established hitherto. The theory that want to regard the construction of the genetic code as a “frozen accident” [1] seems still the prevailing paradigm among many. Indeed, it is just a way of giving up, to say that it not at that time or yet have been found any other convincing explanation of the code. A main problem has been the seemingly random distribution of codons to the 20 canonical amino acids (aas) that make up the building stones of proteins.
More purely mathematical approaches to the problem have been taken by relatively few, as it seems from published articles. Among those who have focused on the mass of aas and its distribution are for instance [2-7].
Arithmetical contributions are often distrusted with the argument that many different mathematical regularity surely can be found that might be just accidental.
However, mathematics may be regarded as a language for a deeper level of concepts, underlying the biochemical and physical ones. Numeral series appear for instance on the atomic level in Rydbergs formulas for spectral lines of hydrogen and in the 2x2-series (x = 5-0) behind the periodic system. The hypothesis seems natural that some kind of similar arithmetical scheme could continue operating on the more complex levels of biochemistry and the construction of the genetic code.
In fact, a related numeral series has been shown to highly correlate to the structure of the genetic code in several different aspects [8]. It was argued that such a structure, dimensionally, geometrically or numerically interpreted, should perhaps not be recognizable at the very first steps of syntheses in the evolution of the code, just gradually revealed by spontaneous self-organization. (The periodic system of elements, for instance, became visible first after long periods of fusion of heavier elements after Big Bang.) The found regularities concern the distribution of atomic mass of amino acids on codon domains. The opinions against the importance of mass on the levels of biochemistry and cell metabolism are discussed.
In an essential aspect it differs from other’s calculations in starting from a 24 codon table for the 20 ‘classical’ aas, thus including not only two sets of Arg, Ser and Leu with two different codons but also the codon AUA for Ile, only differing from AUY in 3rd base type.
This paper might be regarded as a follow-up of that article, which gives reasons to mention some of those earlier main observations:
The atomic mass of aa side-chains (R) were summed in groups, i.e. ‘codon domains’ of aas after 1st and 2nd base in their codons and denoted G1-, G2-, C1-, C2-domains of aas etc. It implied 4 sums in 1st base order, 4 in 2nd base order:
G1 = 191, G2 = 411; U1 = 463, U2 = 437
C1 = 353, C2 = 133; A1 = 497, A2 = 523
The codon domains G1 + C1 of aas became equal to G2 + C2 = 544, as the sums U1 + A1 equals U2 + A2 = 960. (It should be noted that the basic two Arg and Lys here were counted as charged in agreement with Wohlin and Karlson [8,9].
A basic series of integers 5-4-3-2-1-0 with exponent 2/3 times 100 (the “ES-chain”) was tested, thus the cubic roots of the elementary x2-series x 100. Abbreviated it gave the numeral series 292 - 252 - 208 - 159 - 100 - 0, the numbers referred to as 5’- 4’- 3’ - 2’- 1’- 0.
Additions and intervals in this series showed up to correlate more or less exactly with the atomic mass of aas summed in codon domains of different kinds. The series was called the ES-chain.
Two times first three numbers in the chain gave the total of R for the 24 aas and were divided on codon domains as follows:
5’+ 4’ + 3’= 752 x 2 = 1504.
5’ + 4’ = 544 = G- plus C-domains
5’ + 4’ + 2 x 3’ = 960 = U- plus A-domains
The very number 24 of aas correlates with two times 5 + 4 + 3 in the basic series.
A reference was made to the 5-, 4- and 3-merous plans of plants, the 5- and 4-merous ones from dicotyledons, 3-merous ones from monocotyledons, surely not random numbers.
The aa sums of single base G- and C-domains included displacements of 1’ and 2’ in the ES-chain:
G1 = 5’ – 1’ (–1) = 191, C1 = 4’ + 1’ (+1) = 353
G2 = 4’ + 2’ = 411, C2 = 5’ – 2’ = 133
The correspondence was noted with a displacement of Arg, charged 101, from G1 to C1 and in 2nd base order a displacement from C2 to G2 of 159 = Arg + Pro + Gly + Ala with codons CG, CC, GG and GC. A similar displacement of Tyr 107 = interval 3’ – 1’ (–1) from ES-numbers 544 and 2 x 208 gave the U2- and A2-domains.
A central finding was the table on aas with “mixed” and “non-mixed” codons, 12 in each; “mixed” codons here meaning one of the first two bases in the triplets from the G+C-group, one from the U+A-group.
Mixed codons, aas = 2(5’+ 4’ – 2’),
Non-mixed codons, aas = 2(3' + 2')
The table on mixed codon domains of aas gave an astonishingly regular 2D-table (or 3D if the N-Z-division should be included): the 3 rows adding up to 385 - 209 - 176 and the 4 columns adding up to 209 –/+1 and 176 +/–1. (N = 2 x 176 –1, Z = 2 x 209 +1.)
Further, ES-numbers were found again in groups of aas deriving from the different stations in glycolysis and the citrate cycle respectively if Ala and the AG-coded Ser2 were considered as derived from oxaloacetate. All U1- and/or U2-encoded aas from stations in the glycolysis add up to half the total = 752.
The sum of aas from α-ketoglutarate became 543 = 5’ + 4’, –1, those from oxaloacetate 209 = 3’, +1.
The ES-series showed on congruence in illustrating the condensation of backbone parts (B-chains) of aas in groups of six: (5’+ 4’) – 1’ = 444 = 6 unbound B-chains, minus interval 3’ – 1’ = – 108, equal to 6 H2O, giving 336, the sum of 6 bound B-chains = 544 – 208.
of the ES-series concerned the so-called 4-fold degenerated codons. The sum of all aas with differentiating 3rd base were found to be 2 times 5’ (292) and close to equally divided on the G1+A1-domains, 584 and the C1+U1-domains 584 (+1). 4 times the following intervals 5’ to 3’, 40 and 44, were found as the two groups of aas with “4-fold degenerated” codons among the non-mixed (–1) and mixed codon domains, here called “2-base-coded”.
In a rather comprehensive section the ES-chain was compared with the same numeral series 5-0 with simpler exponents. Just a few annotations here:
The basic series x1 read as triplets 543 + 210 = 753 times 2 gave the total sum of aas 1504 +2.
The x4-series, showed in first 3 numbers a similarity with the ES-chain: 625 – 81 = 544, the G+C-domains of aas, and 625 + 256 + 81 = 962, the U+A-domains of aas +2.
In the x3-series the two middle numbers 27 and 8 with interval 19 appeared related to the table on mixed codon domains: rows 1, 2 and 3 equal to 11 times 27 + 8, 27 – 8, and 2 x 8. The sum 27 + 8 = 35, divided in a quotient 3/2, times 11 gave the sums 231 and 154 in which the table was divided.
It was also observed that the inverted squares of 33 and 23 times 103 approximately gives the aa domains G1 and C1, more exactly 546, which times 6 gives the total of 24 aas R+B. An association was mentioned, however not developed, from the numbers 27 and 8 to the group theory of elementary particles in “The Eightfold Way” by Gell-Mann and Ne’eman [10].
The x3-series include also the number 64 of possible triplets, reduced to 27 in the basic step 4 → 3, i.e. 24 aas and 3 stop codons.; the 24 aas divided in 3 eighths after type of the 3rd base.
In the 2x2-series behind the periodic system, 50 - 32- 18 - 8 - 2 - 0, the codon domains of aas corresponded to the ‘angled’ sums 32 + 2 times the factor 16 = G+C-domains 544, and middle numbers 18 + 8, times 16 = 416 (= 2 x 3’ in the ES-chain), giving the addition to the U+A-domains 960. The spread of aa sums on mixed and non-mixed encoded aas appeared also in the 2x2-series: 385 among mixed-encoded aas –1 as 32 – 8 times 16, (an interval here as in the ES-chain) and among the non-mixed encoded aas 2 x 18, x 16 = 576 = A+U-domains +1, and 8 + 2, x 16 = G+C-domains +1.
These comparisons with simpler exponent series suggested an eventual stepwise development of exponents to the basic series 5-0, the division of 5 from its ends towards the middle 3 and 2: x4 → x3 → | ← x2 ← x1, giving rise to the exponent 2/3 in the ES-chain.
The following research points to some more fundamental features in the organization of the genetic code, equally based on the series of integers 5 - 0 and closely related to the ES-chain described above. The first observations were inspired by a proposal by Di Giulio [11] that it could be the distances of aas from a mean value (Mv) that might be interesting. Already in the earlier article it was noted that the quotient between the sums of aas lighter and heavier than Mv were approximately 2/3 (600 and 904).
The single word “mass” here will refer to the number of nucleons, i.e. the “atomic mass” of most common isotopes and to only the side-chains (R) of aas when nothing else is mentioned.
2.1 Totals, atom kinds and codon domains
It was found that an approximate 3/2-division of the total sum R = 1504 of 24 aas, when ordered in a weight series around the Mv, appears not only in the total mass of aas but also in the division on atom kinds and on codon domains.
As stressed above the calculations here depart from a 24 codon table for the 20 ‘canonical’ aas, thus including not only two sets of Arg, Ser, Leu with two different codons but also Ile Ile2, AUA, only differing in 3rd base type.
Further, in these first calculations, the basic two Arg and Lys are taken as charged after Karlson (1976) [9].
The aas form two series around the mean value (Mv) 1504/24 = 62.66...(62 + 2/3), Figure 1.

Figure 1. The two weight series of aas around Mv
Lighter than Mv, the “L-chain”: 14 aa
Heavier than Mv, the “H-chain”: 10 aa
Taking all aas as uncharged, the sum deviates with a single unit from the big integer 1500, the sum of the series 5 → 0 times 102. (With eventually only Glu charged, from α-ketoglutarate, the only 5C-molecule in the citrate cycle, the total 1500 gives Mv 62.5, 1/6 less.)
Apart from +4H in the H-chain the H-atoms are equally divided 74 — 74 in the chains. Deviations from 1500 raise the question about pH- and pK-values at the origin of the genetic code. (To get the big integer at a single moment it seems necessary to imagine some dramatic event or a special environment where a very basic layer met a very acid surrounding, creating a polar axis between very high and very low pH-values simultaneously.)
Counting on a whole of 1501, the three different divisions of aa sums on L- and H-chains appear as in Figure 2.
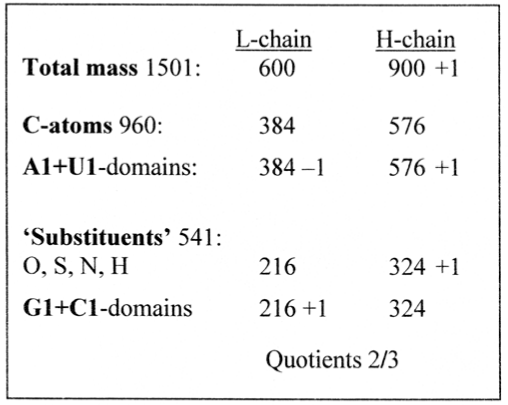
Figure 2. 2/3-divisions of total mass, C-atoms versus other atoms and codon domains of aas A+U and G+C
2.2 Pythagorean numbers
The factors in 600 - 384 - 216 in these 2/3-divisions, 300 - 192 - 108, are easily recognized as 12 times the squares of 5 - 4 - 3, a simple scheme of disintegration from 5 and associated with the ‘Pythagorean triangle’ (The sign “∼” here used for "almost or equivalent with"):
52 x 12 = 300, x 5, ∼ total mass as 1500
42 x 12 = 192, x 5, ∼ C-atoms = 960
32 x 12 = 108, x 5, ∼ Rest, other atoms = 540
Pythagorean numbers1) have been found in parts of the genetic code by others (shCherbak 2003) [4], however not in the same context or kind of calculations and with another factor.
_________________________________________
1) A footnote:
The factors as 384 and 576, 216 and 324 are all numbers in the Pythagorean musical scale according to data from Négadi [12].
_________________________________________
A factor × 5 after factors × 3, × 4 (=12) seems to follow naturally, reaching a total sum of 1500. It should be stressed, however, that this does not explain the division of factor 5 in 2 and 3 around the Mv of an aa.
2.3 Factors 192 - 84 - 108 in the ES-series
2.3.1 A displacement of 4 gives ES-numbers: The disintegration of the total as 1500 into 960 and 540 gives an interval 420. (16 – 9 = 7, x 3, x 4 = 84, x 5 = 420.). A simple displacement of 4 units from this interval to 540 gives the codon pair domains of aas A+U and G+C in the ES-series, thus equal to C-atoms and other atoms when counting on a total of 1504.
5 x 192 = 960 = 5’ + 4’ + 2 x 3’ = A+U
5 x 84 = 420, – 4 = 416 = 2 x 3’
5 x 108 = 540, + 4 = 544 = 5’ + 4’ = G+C
2.3.2 The factors as intervals in the ES-series: The ‘Pythagorean squares” 16 and 9 times 12 = 192 and 108 with the difference 84 appears as intervals in the ES-series 292 - 252 - 208 - 159 - 100 (abbreviated), referred to as 5’ - 4’ - 3’ - 2 - 1’ - 0.
5’ – 1’ = 192 = 4 x 3 x 16, 4 steps, divided in
5’ – 3’ = 84 = 4 x 3 x 7, two steps, and
3’ – 1’ = 108 = 4 x 3 x 9, two steps
The relation to the ES-series of integers 5-0 with exponents 2/3 times 100:
[52/3 –1] x 100 ≈ 192 = 5’
[32/3 –1] x 100 ≈ 108 = 3’
It looks as Arg, uncharged = 100 = 1’ just was added to these odd stations 5’ and 3’.
The G1-domain of aas = 191 corresponds in itself (–1) to the whole interval 5’ to 1’, as if it represented intervals as such?
The ES-chain seems to represent a secondary development in step 4 to 3. There the number 7 for nitrogen N is found, characterizing the genetic code and proteins.
Further, in the basic series 5-4-3-2-1-0, the division 9 - 6 of number 15 appears in step 4 → 3 through elementary additions 5+4 and 3+2+1-0. It is possible to simply read the sums of C-atoms and other atoms in this way: 9-6-0 and 5-4-0.
A single displacement of 16 units betwen the L- and H-chains in the weight series would give 2 times the ES-numbers 5’, 4’ and 3’, a division in the step 5’ - 4’.
600 – 16 = 584 = 2 x 292
904 + 16 = 920 = 2(252 + 208)
2.4 Number-base transformations
In the preceding paper (Section 6) [8] it was suggested on the basis of several examples that transformations between number-base systems (nb-x) as between nb-10, nb-8 and nb-6 could be a hidden reference system in the genetic code. Rewritings of lower nb-numbers with digits from nb-10 were freely used. In the weight series such references appear astonishingly clear, Figure 3.
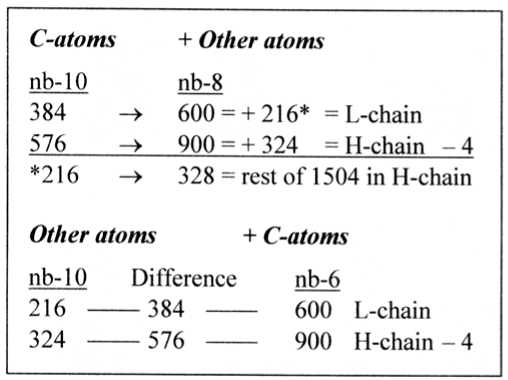
Figure 3. Mass sums of the L- and H-series of amino acids given from their sums of C-atoms in nb-8 and from their sums of other atoms in nb-6 through transformations between nb-10 to nb-8 and nb-6
A reciprocal reference system seems active between parts and totals; the nb-systems representing 2 times 5, 4 and 3. It might be one reason for the relative stability and universality of the code.
A relation between the whole L- and H-chains appears through a second transformation nb-10 to nb-8:
L-chain 600 in nb-8 = 580 rewritten.
580 in nb-10 = 904 in nb-8, the H-chain
Both groups of C-atoms can be derived from number 126, 2 x number 63, ∼ Mv of an aa and also a factor in the total 3276 of 24 whole aas R + B. Repeated transformations nb-10 to nb-8 are here marked as arrows:
126 → 176 → 260 → 384
126 → 176 → 258 → 382 → 576
Cf. 126, 176, 258 and 384 in number pyramids on the 2x2-chain (Section 7, [8]).
For complementary material, see supplementary files 1 and 2.
For more on such nb-transformations and other material, see http://www.u5d.net/Genetic-code/index.html
2.5 Synthesis of hexoses, an association
The factors 192, 108 and interval 84 give associations to the synthesis of hexoses as it often is summarized, Figure 4.
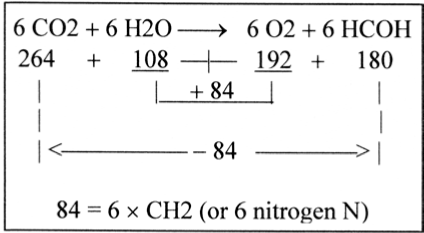
Figure 4. Summary formula for the synthesis of hexoses
Cf. CO2 as O=C=O with the form of bound and charged ∼COO- -groups à 44 A:
264 = 6 O + 6 C=O = 192 x 1/2 + 84 x 2
180 = 6 O + 6 CH2 = 192 x 1/2 + 84
In a simultaneous process [9] nitrogen gets built in as NO3- (62 A) → NO2- (46 A) ... → NH4+ (18), Here the element molybdenum (Mo) takes part in the first step NO3- → NO2- = -16.
Molybdenum, 42 Z, 96 A = 1/2 x 84 Z and 1/2 x 192 A. Just a coincidence?
The numbers 192 - 108 - 84 appear again if transformed between nb-systems, Figure 5.
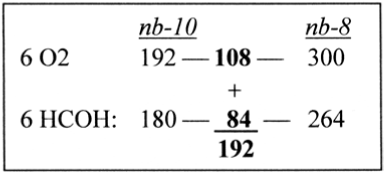
Figure 5. Transformations nb-10 to nb-8 of right terms in the formula for the creation of hexoses
300 in nb-6 = 108 in nb-10, and 180 in nb-6 = 84 in nb-10.
(Perhaps notable also is that a hexose with the mass 180 in nb-16 becomes 384 = 2 x 192 in nb-10.)
2.6 Some 3/2-divisions in the ES-chain
The 3/2-division was a remarkable feature in the table of mixed codon domains of aas with the sum 2 x 385 [8]. (To repeat: ”mixed codons” means one of the first two bases in the codon of an aa from the G+C-group, one from the A+U group.) In that table the row 1 = 385 got divided in G1 + C1 = 154, A1 + U1 = 231, and the rows 2 + 3 with lighter aas G1+C1 = 231, A1+U1 = 154; thus divisions in 2 and 3 times the factor 77.
In the A1+U1-coded group the same quotient appears between those with mixed and non-mixed codons and closely also within the non-mixed group in the divisions on the L- and H-chains:
Mixed — non-mixed codon domains:
L: 385 — 575 :H
C-atoms:
L: 384 — 576 :H
A1+U1-coded aas:
L: 383 — 577 :H
Within the non-mixed codon group of aas 575:
L-chain 231-2, H-chain 346, quotient ∼ 2/3.
In the mixed codon group of G1+C1 (also = 385) Gln breaks this straight connection with L- and H-chains: L-chain = 154 +5 = non-mixed group, H-chain 231 – 5.
However, in the division of 544, equal to G+C-domains and to other atoms than carbon, the quotient ∼ 3/2 x 109 appears between aas with mixed and non-mixed codons:
Mixed codon domains:
C-atoms 544 – 100. Other atoms 326
Non-mixed codon domains:
C-atoms 416 + 100. Other atoms 218
ES-numbers in the division on C-atoms: 5’ + 4’ – 1’ and 2 x 3’ + 1’.
2.7 Codon domains correlating with atom kinds
The figure 2 (Section 2.1) clarified the nearly equal mass sums of codon domains and atom kinds. Already in the earlier paper [8] the numeral equivalence was underlined between the whole A+U- and G+C-domains of aas with the total of C-atoms and ‘substituents’ respectively (960 and 544). Figure 2 shows that the division within these groups also closely follows the general 3/2-scheme in the weight series. It seems to prove that the striking correlation is not a random one, that it indicates interdependency on some deeper level. (Both codon domains of aas include naturally both kinds of atoms.) How to explain it?
In fact, the correlation might be an evidence of the general arithmetical approach as relevant in the interpretation of the genetic code.
Some examples indicate that the division of 960 in the ES-series into 5’ + 4’ = 544 and 2 x 3’ = 416 lies behind and governs both the divisions of codons and of atom kinds:
A first illustration: the disintegration of 544 into the interval 177 and 3’ + 2’ = 367 in the ES-chain. –/+ 1, gives 176 and 368 (with the difference 192). Dividing 416 equally on these numbers gives the 2- to 3-division of the C-skeleton, Figure 6.
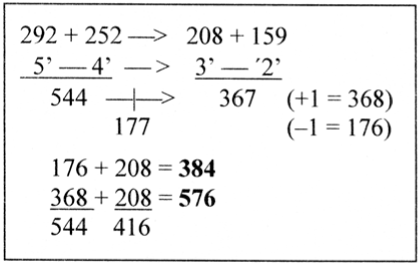
Figure 6. Adding 208 to the disintegrated parts of 544 in the ES-chain, 177 and 367 (= 3’ + 2’), –/+1, gives the 2/3-division of C-atoms
The steps in the ES-chain outwards correspond to a trend towards more AU-rich codons. A1 = 177 and U1 = 208 among mixed-encoded aas. 367 + 208 corresponds to the sum of non-mixed-encoded A+U-domains.
(The number 176 corresponds to the ”2-base-coded” aas with mixed codons = GU+CU+UC+AC.)
The order between ”strong” and ”weak” bonds [13] of codons for aas in the ES-chain outwards regarding first two bases becomes 5, 5–1, 5 +1, i.e. 5-4-6: from mixed codons with 5 bonds to aas with 4 and 6 bonds in the non-mixed encoded groups. (It looks like an inscription for the factor 546 in the total R+B of 24 aas, 3276.)
Cf. mass of the codon bases unbound transformed to nb-8 [8]: G+C in nb-10 = 262 = 386 in nb-8, connected with mixed-coded aas, and A+U in nb-10 = 247 = 367 in nb-8, 3’ + 2’.
A second example of 416 as a simple addition is given in table 1, counting on a total of R =1504:
Table 1. Adding 416 to the A1+U1-domain of aas gives its mass of C-atoms
Codon domains |
C-atoms |
Substituents |
Sums |
G1+C1 |
324 |
220 |
544 |
A1+U1 |
220+416 |
324 |
544+416 |
The same pattern –/+ 12 in the division of 544 appears in 2nd base order. In both cases the addition of 416 gives the sum of C-atoms in the A+U-domains, 636 and 648 respectively.
Apart from 416 the figures shows a reversed relation between C-atoms with valence 4 and the rest with valences 3-2-1, i.e., the mass of this rest atoms in the A+U-group. It seems to indicate a change in directions outwards to inwards in the codon groups, possible to see as an antiparallel relation in codons that gets angled to a perpendicular one in the division on atom kinds in the step 4 → 3 of the basic series 5-0.
A third illustration of 416 as a separated addition is given when adding sums of aas in first and 2nd base domains, here with a deviation of +/– 2:
G1 + G2 = 602, + 416 +2 = 1020 = A1 + A2
C1 + C2 = 486, + 416 –2 = 900 = U1 + U2
A note about number 416 and the x3 and 2x2-series:
Number 416 as 2 times the 3rd number 32/3(x 100) in the ES-series corresponds to the 3rd number 27 in the x3-series, the middle step of which gave the factors in the table on mixed-coded aas (Wohlin 2015). The quotients 416/27 ≈ 15.4 and.416/18 (the 3rd number in the 2x2-series) ≈ 23.1 are 1/10 of the 2- to 3-division in that table.
The correlation between the G+C-coded aas and sums of the ’substituents’ showed up in table 1 above divided in 3 x 108 = C-atoms and the rest = 2 x 108 +4.
C-atoms 324 in the G1+C1-groups in this table are divided in 108 on G1 and 216 on C1, thus in agreement with factor 108 (Section 2).
The total of G1+C1-coded aas, in L-chain 217, correspond to the other atoms –3, those in H-chain 327 to the sum of C-atoms +3, counting on the total 1504. The division on mixed and non-mixed coded aas is close to the same:
H-chain — L-chain:
327 — 217 (324 +3, 216 +1)
Mixed — non-mixed coded aas:
326 — 218 (324 +2, 216 +2)
2.8 Atom kinds after valences
A final aspect on the codon groups 544 and 960 and their relations is shown below with reference to the total 1504 of aas = 2(5’ + 4’ + 3’) in the ES-chain.
The mass division on atom kinds after valences is simply derived from 2 x 5’ (292) = 584, – 2 x 3’ (208) in two steps and could illustrate the substitution of oxygen with nitrogen in metabolic processes on the way to the protein world:
584 – 208 = 376 = O + S + H, valences 2 and 1
+ 376 – 208 = 168 = N, valence 3
= 960 – 416 = 544
= C-atoms 960, valence 4, and other atoms 544.
3.1 Molecular groups
An evolution of the code along the weight series is only partially possible to imagine.
Such a growth should imply stepwise additions of molecular groups with different properties and functions, adding atomic mass of 12 - 15 (CHx), 14 - 17 (NHx), 16 - 17 (OHx) and 32 - 33 (SHx) as to a ‘linear’ series of B-chains. It is possible to see single such steps of +14 and + 16 as for instance 1 → 15 → 31 → 45 → 59 → 73 from Gly to Ala-Ser-Thr-Asp-Glu, which of course makes gaps in the weight series very natural. However, they hardly correspond to the actual biochemical construction of the aas in such a simple way. At the same time clusters of aas in mass areas 42 - 47, 57 - 59 and 72 - 75 include aas of different origin, synthetic pathways and character.
(The only aa that does not seem to fit in any ‘natural gap’ is His 81, possibly connected with the fact that it is the only aa that not derives from stations in the glycolysis and citrate cycle but from the A-base.)
3.2 Valences of C, N, O/S, H and three aa groups
Dividing the R-chains of aas according to “characterizing” atoms and their valences 4-3-2-1 gives three groups, those including 1) only CHx-molecules, 2) those with NHx and 3) those with O/SHx + H respectively. Some general observations:
C-atoms get distributed with 50 on the NHx- and O/SHx-groups, equally divided 25 - 25, and 30 on the CHx-group.
H-atoms in a total of 1504 were 152 = 4’ – 1’ in the ES-series. They are also distributed close to equally on the NHx- and OHx-groups, 46 and 47 respectively, halving the interval 4’ to 2’ = 93 in the ES-series. The CHx-group includes 59 H = 2’ – 1’ in that series.
Further, there might be a reason to note that the 24 aas include 12 N-atoms with valence 3 and 12 with valence 2, including the 2 S-atoms, in valences a 3/2-relation 36/24.
Pairing the three groups in different ways reveals correlations with series earlier dealt with:
The CHx- and NHx-groups versus the O/SHx-group shows up to give the same mass division as between H- and L-chains in the weight series, +/-1, 905 and 599, Figure 7. This similarity appears when Asn and Gln are taken as derived from Asp and Glu in the O/SHx-series and are included in that group of aas.

Figure 7. Three series of aa types: masses divided on L- and H-chains
Regarding valences the division represents a polarity in the step 3 — 2 of the basic series 5 - 0, as two-way directed, between steps 4 → 3 and 2 ←1, as if this polarity led to the approximately mass division 3 to 2.
The similarity with divisions in the weight series appears as along a ‘perpendicular’ coordinate axis. (Very hypothetically the +/- 1 in several contexts may be essential, representing transitions to another axis during different polarization steps? Cf. H+ and e– as fundamental forces on the biochemical level.)
In the sums of the CHx- and NHx-series the division on L- and H-chains become almost the same as the one between ‘substituents’ and C-skeleton in the whole H-chain, which was 328 and 576, and with the division on codon domains G1+C1 and U1+A1, 327 and 577 (Section 2).
The lonely Phe in the H-chain could perhaps be one aspect on why Phe seems to belong to the ‘wrong’ Class II in the aa division on aminoacyl-tRNA synthetases.
The three special aas from P-enolpyruvate, the aromatic Phe, Tyr and Trp, have the mass sum 328, the other aas in the H-chain then 576, which implies a similar division as between C-atoms and the 'substituents' in the H-chain. (These 3 aas becomes here distributed one in each group, perhaps not a coincidence.)
Pairing the three groups another way, with a total of 1504, they get conneted directly to the basic series 5-0 read as two triplets 5-4-3 → ← 2-1-0 (–2):
O/SHx + NHx series = 1085 = 2 x 543 –1
CHx series = 419 = 2 x 210 –1
Interval 666, the division = 753 +/– 333. Cf. in the ES-series [8]. 752 = (52/3 + 42/3 + 32/3) x 100 = 544 + 208.
The CHx-group (+1) is equal to the interval 5 x 192 — 5 x 108 when counting on a whole of 1500 (Section 2), in that case corresponding to the difference between the mass of C-atoms and other atoms, 960 – 540.
The valences of “characterizing” atoms appear in this pairing in opposite order to the numbers of the basic series, instead as number of steps 1-2-3-4 from 5. It correlates for the most part with the fundamental opposition between the hydrophobic, inward direction of the CHx-group from lower numbers and the more or less polar outward direction of the O/SHx- and NHx-groups from higher numbers.
(As for polar versus non-polar aas, the groups here deviate from a usual division: Trp in the NHx-group and Met in the O/SHx-group are regarded as non-polar. Moving these two aas to the hydrophobic CHx-group its sum becomes 3 x 208 and the two polar groups becomes 880 = 3 x 292 +4, thus an opposition between 5’ and 3’, times 3, in the ES-chain if one counts on an eventual original total of 1500.)
Some aspects could be added on the O/SHx- and NHx-groups and their mass relation, 600 –1 and 486:
In these two groups the division of their total mass sums equals the one between C-atoms and other atoms, which follows from the equal division of C-atoms. There again appear different kinds of polarizations of the same numbers as along different coordinate axes (–/+ 1):
NHx: C-atoms 300 — Rest 186. Sum 485 +1
O/SHx: C-atoms 300 — Rest 299. Sum 600 –1
Sum: 600 485
The division of the two groups with the sum 2 times the basic triplet 543 –1 approximates the one found between codon domains:
543 +/– 58 = 601 and 485.
There is the similar division of summed codon domains in 1st and 2nd base order:
G1 + G2 = 602, ∼ O/SHx
C1 + C2 = 486, ∼ NHx
It was found (Wohlin 2015) that the interval 2’ - 1’ = 59 in the ES-chain –/+1 = 58 and 60, was the differences between codon domains of aas G1 - C2, C1 - G2 and A1 - U2 and U1 - A2.
(The division approximates also the Z/N-division within the G+C-group 544: 300 Z, 244. The Quotient Z/N in the total 1504 is close to √3/2.)
A pairing of codon domains in 1st and 2nd base order after the keto-/amino acid polarity gives approximately 3/2-relations:
G1 + G2 = 601 +1
U1 + U2 = 902 –2
The similar close to 3/2-division within the A- and C-groups is given with –/+ the CHx-group 419:
2021 Copyright OAT. All rights reserv
A1 + A2 1020, – 419 = 601
C1 + C2 486, + 419 = 905, if – 3H = 902
These numerical relations including different sets of aas between codon domains and the molecular groups might just point to numerical functions of codon-dependent aas.
4.1 Two similar numbers in the spread
The original question [11] behind this research, if it eventually could be the distances of aas from a mean value that might be of interest in the code, led to some first observations of similarities:
The spread of mass within the two series, the L- and H-chains, 1-59 and 72 - 130, encompasses both 59 integers. The number 59 is the R-chain of Asp and equal to the interval 2’ - 1’ in the ES-chain. Cf. the polarization between O/SHx- and NHx-groups in Section 3.2 above.
The total spread of the series Gly to Trp = 1 - 130. the sum of these aas furthest from Mv = 131 and the sum of aas closest to Mv, Asp and Gln = 59 + 72, is the same, 131.
Could these similar numbers 131 and 59 have a deeper sense? Arithmetically there are approximate relations through 2/3 as an exponent to the total 1504 and as a factor between them:
15042/3 = 131.27., x [2/3]2 = 58.34.
The interval Asp — Gln where the ∼63 is positioned represents 13 steps, divided by Mv approximately 4 to 9, the squares of 2 and 3.
The number of molecular groups (Section 3.1) in aas = 104 in R, 120 in B-chains, stretches from 5 in Gly to 15 in Trp: 15 as the sum of the basic series 5 → 0 perhaps a limit? The Mv of groups (CHx, NHx, OHx, SHx) in R +B becomes 1504/224 = 14.625, (≈ half of the first number in the ES-chain 292.4 x 10–1):
32 x Mv 14.625 = 131.625.
22 x Mv 14.625 = 58.5.
In the 2x2-series half the central numbers 18 - 8 gives the factors 9 and 4. The sum 18 + 8 = 26 is a factor both in the number of groups in R 104 and in the total spread 130 = 5 x 26.
Regarding number 59 as the interval 2’ — 1’ in the ES-series, a simple reading of 2-digit numbers in the basic series 5 - 0 could illustrate a derivation of the two spread numbers as intervals 129 and 58, Figure 8. Here number 13 represents the gap 72 - 59, Gln to Asp (Figure 8).
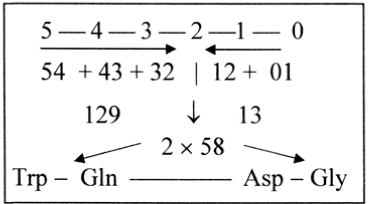
Figure 8. The spread numbers as intervals 129 and 58 derived from a 2-digit reading of the basic series 5 - 0
Biochemically the number 59 might be seen expressed in the acetylgroup CH3-COO–, acetyl∼CoA a crossroads for developments to different kinds of substances. Its inclusion in the citrate cycle, added to oxaloacetate 132 A (charged 130), leads to citrate 192 A, charged 189 =130 + 59. The spread numbers might perhaps be interpreted as parts of this fundamental number 192, equal to 5’ – 1’ in the ES-chain. In this series Asp R + B = 133 = 5’ – 2’ and Asp R = 59 = 2’ – 1’.
4.2 Distances of aa masses from Mv, +/– 277.33
The sum of distances of aa masses from Mv in the two series becomes the number of aas, 10 and 14, times Mv, minus their mass sums:
5 x 2 x Mv = 626,66.,
4 x 2 x Mv = 501.33.
> 877.33.
3 x 2 x Mv = 376
904 = 626.66. + 277.33. = H-chain, 2 x 5 aa
600 = 877.33. – 277.33. = L-chain, 2 x 7 aa
The sum of the first two numbers, 2(5 + 4) x Mv = 1128, corresponds to the sum of C- and N-atoms with valences 4 and 3, and the 3rd number 2 x3 x Mv, 1/4 of the whole, corresponds to the O- , S- and H-atoms with valences 2 and 1 (Section 2.8).
About the Mv-numbers ∼ 627 and ∼ 877 it could be mentioned that close to these numbers appear in a crosswise adding of aa domains after the keto-amino acid polarity:
G1 + U2 = 628, ≈ 10 x Mv + 4/3
C1 + A2 = 876, ≈ 14 x Mv - 4/3
(These groups include of course to sets of the GU, GA, CU and CA domains = 385, compensated by the same sum in the opposite crosswise additions. G1 and C1 domains have both 5 aas, U2 and A2 domains both 7 aas. The equal numbers of aas in the domains could indicate that the 2nd position in codons is the primary one for the U+A domains, the 1st position for G+C-domains.)
Now, the sum of distances 277.33... happens to be exactly 2/3 of 416, 2 x 3’ in the "ES-series". However, although very close to 416, the number is there an abbreviation. In the 2x2-series behind the periodic system, times 16 (Section 5.2.1, [8]) the exact number 416 appears as 16(18 + 8) in the middle step. Note the factor 26 again. The question arose if the number 277.33, was just a coincidence or could indicate some underlying system?
The sum of distances 277 +1/3 in Figure 9 becomes divided in 192 and 84 +4/3.
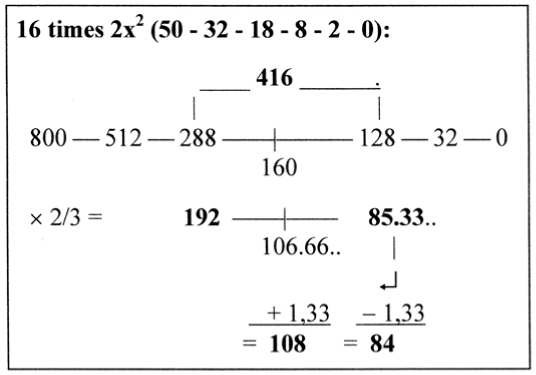
Figure 9. 2/3 of number 416 in the 2x2-series x 16
Thus, moving 4/3 from 85.33 to the interval 106.66 gives 192 divided in 108 and 84 These numbers were the factors in section 2 and intervals in the ES-series, however in a changed order, opposite to the one in the ES-series: 84 = 5’ — 3’, 108 = 3’ — 1’, 192 = the sum 5’ — 1’. (A similar opposition appears in the numbers 14 x Mv = 877.33, circa 3 x 5’ in the ES-chain, and 10 x Mv = 626.66, roughly 3 x 3’ in that chain.)
A way to describe this relation with the ES-series could be Figures 10a and 10b below, the latter from the primitve background model behind this research (Section 2, [8]). There the series 5 → 0 represent dimensional degrees, where higher degrees are thought to polarize into complementary structures, defining next lower degree; the debranched degrees 1 to 2... expressed in external motions or meeting "the other way around" in step 3 → ← 2. 84 is the sum of first two intervals in the ES-chain.
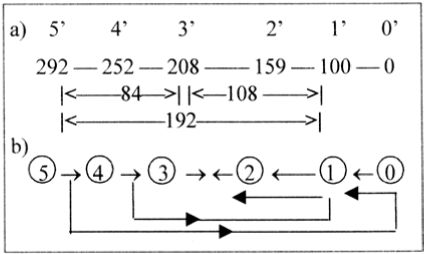
Figure 10. a) Intervals in the ES-chain, x =5 - 0 with exponent 2/3 x 100,
b) The background model of possible dimensional steps.
416 in the 2x2-series times 16 is built on 18 and 8 with the quotient [3/2]2, and an underlying level may be expressed in the 3/2-relations of the H- and L-chains in the weight series above. (Cf. also the proposed derivation of spread numbers from Mv of 104 groups in R-chains (Section 4.1), expressed as 9/4 x 26 = 58.5, → x 9/4 = 131.625.
A speculative note:
The inversions of 9 and 6 as factors in the L- and H-chains add up to 0.2777... = 2 x 0,1388. (The number differs from 277.33. with [2/3]2 x10x.)
Could the spread of aas in the weight series have something to do with the 3rd spectral line of hydrogen in the Balmer series, 0.1388 from Rydbergs formula 1/22 - 1/32? Masses of U-, A- and G-bases were derived from quotients between these three first spectral lines times 102 (Section 7, [8]). Now, there is the number of aas = 2(5 + 4 + 3) = 24:
The inversion (/\) of 24, x 104 = 416.66; x 2/3 = 277.77. 1/3 equals factor 1/22 – 1/32 in Rydberg’s formula for this 3rd spectral line (x10x).
(277.77. = 1/2 x 555.55..., the inversion of 18, ∼ H2O, x 10x.)
5.1 Construction of the coding bases
The aas Asp and Gln closest to Mv are those that contribute with NHx-groups to Gly in the construction of inosine, the parent to the purine bases A and G. Asp as a whole also makes up a big part of orotate, parent to the pyrimidine bases U and C, adding carbamoyl(∼P), which often derives from CA-encoded Gln.
The masses of the central Gly 75 and Asp 133 were noted as each other’s inversions ∼ 3/4 and 4/3 x 100 and their sum 208 as equal to 3’ in the ES-series [8]. Their difference 58 returns in the spread numbers of the L- and H-chains.)
Further, Gln contributes to a preliminary stage (chorismate) in the synthesis of Trp that resembles a base.
The aas closest around Mv are also those that ammoniate the B-chains of other aas. Together, these facts emphasize the breakpoint between the H- and L-chains as an essential center.
The interval between purine and pyrimidine pairs of bases is 63, the approximate Mv mass of an aa:
63, ∼ Mv, = [G+A] - [C+U] = 286 - 223
Some other annotations about Mv of an aa ∼ 63:
- It is a factor also in the total R + B of aas, 3276 = 63 x 2 x 26 (18 + 8).
- In the ES-series it is 1/4 of 4’ = 252, and 3/4 of the number 84 (5’ - 3’).
- 5002/3 ≈ 63 (62.996.); 500 = 5’ + 3’ in the ES-series and 1/3 of 1500, eventually the original total of R.
- 63 is also close to 10 x 2π (62.83.)
In the bases the numbers 192 and 108 with the interval 84 (Section 2) are found again. The rings of a base pair, G or A + C or U, contain 5 + 4 C-atoms = 9 x 12 = 108 and 4 + 2 N-atoms = 6 x 14 = 84. Thus, the sum of C + N is 192 in the rings of a base pair.
2 base-pairs → 3 base-pairs:
12 N = 168 → 18 N =252...Sum 420, 7 x 60
18 C = 216 → 27 C =324...Sum 540, 9 x 60
Sum: =384 =576
Hence, there are the same numbers as in groups of aas, although in a different combination of atom kinds.
The equivalence of 384 for 2 base-pairs above with the sum of C-atoms in aas of the L-chain in the weight series could give associations to the ‘fourfold degenerated’ or “2-base-coded” aas. However, only 7 of its 14 aas belong to this group.
(Mass of C-atoms in these seven “2-base-coded” aas = 168, in the other seven = 216; thus the same quotient 7 to 9 as in the N/C-division above and in accordance with step 16 → 9 in the ‘Pythagorean’ squares with the interval 7 in Section 2.2.)
The additional ’tags’ including H in rings for all 4 unbound bases = 125 = 2 x 62.5. Number of atoms in purines versus pyrimidines in the rings is 9 and 6, this quotient 3/2 also noted by others.
5.2 Number 131
It was noted (Section 4.1) that 131 was the sum of both the two aas furthest from and closest to Mv. Number 131 x 4 makes up the sum of the 2 x 4 aas closest around Mv in the L- and H-chains, Figure 11, and the sum of integers in the gap 60 → 71 = 6 x 131 (a 2/3-relation). This gap could also represent a triplet of the closest 1st bases G 151 and C 111 (unbound):
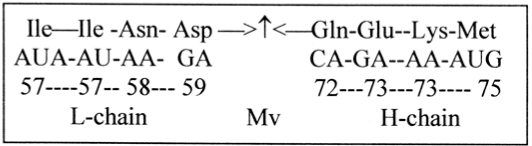
Figure 11. The middle of the weight series: aas around Mv
6 x 131 = 786 = 3 x [G+C]
About the number 131 a molecule as creatine with the mass 131 could be mentioned, created by parts of Arg and Gly sharing an NHx-group: from Arg its end group 59, deriving from the G-base, and from Gly 59 (in its turn from Ser), plus 13, a methyl-group from Met. (Creatine phosphate essential for energy storing and transfer of P-groups ADP to ATP.) The construction of creatine seems in itself to illustrate the total spread of the weight series as 2 times 59 plus 13, the gap 59 - 72.
Another fact to observe in this context is that 131 is the whole mass R + B of an Ile or Leu. A move of the odd ‘extra’ Ile2, AUA, from aa sums R+B in the L-chain to connect with Met AUG in the H-chain (R+B) gives these results:
L-chain 1635, - 131 = 1504 = R-chains, 24 aas
H-chain 1641, + 131 = 1772 = B-chains, 24 aas
The operation could remind of a speculation in the previous paper [8] that B-chains with more mass, equal to more information, and as ‘dipoles’ forming linear “L-waves”, might have preceded the development of side-chains, i.e., the evolution of “T-waves”.
A third fact appears when counting on only 20 aas, without the 4 ‘extras’: the division of R-chains on the H- and L-chains becomes equivalent with the division on C-atoms and ‘substituents’ (+/–1):
C-atoms 20 aas = 960 – 156 = 804, ∼ H-chain +1
Other atoms: 20 aas = 544 – 90 = 454, ∼ L-chain –1
A move in R-chains of only Ile AUA, 57, to Met in the H-chain gives the similar result for 24 aas: H-chain 961 equivalent with all C-atoms +1, L-chain 543 equivalent with all substituents –1. (There are 48 C in 24 B-chains as well as in the H-chain of R.)
These operations that connect B-chains, C-atoms and the H-chain seem to show on polarities along different coordinate axes, following steps in the basic series.
4 → 3. L-waves → T-waves, (from longitudinal waves attributed to gravity and thus connected with mass as a deeper property than charge, to T-waves characterizing the electromagnetic force),
4 → 3, 2, 1 in valences, the relation between a C-skeleton and ‘substituents’,
3 → 2, the mass division within the developed R-chains between H- and L-chains.
6.1 General aspects
Calculations in this and the preceding paper include two sets of 4 aas with 2 different codons, thus including AUA, which only differs in 3rd base type. It becomes a natural demand to at least suggest some explanations of these “extras”, Arg2, Ser2, Leu2 and Ile2.
There are some reasons for counting on 24 aas: Imaging a simple system with only 2 bases, allowing 16 different codons and a half of these dividing into 2 through a 3rd base, a purine or a pyrimidine, it gives 24 codons as 2(5 + 4 + 3); cf. 10 G1+C1-coded aas, 8 A1-coded aas and 6 U1-coded aas. In the common counting with 64 possible triplets, there are 8 “2-base-coded” aas = 32 codons, 8 aas with 3rd base U or C = 16 codons and 8 aas with 3rd base A or G, (5 aas with 2 codons, 3 aas with 1 codon and 3 stop-codons = 16 codons).
There is also the step in the x3-series from 64 → 27, 43 → 33, from possible to realized codons, 33 = 27 disintegrating into 23 x 3 + the three stop-codons.
Another aspect could perhaps be a development along the basic chain 5-0 of products, from 5 x 4 = 20 to 4 x 3 x 2 x 1 = 24 aas. Further, in the suggested reference system of nb-transformations (Wohlin 2015), 20 in nb-10 = 24 in nb-8. If the general genetic system of some reasons only allow for 20 different aas, 4 of these must get two codons.
Principally the four extra aas can of course have quite different reasons for their existence in the code. Biochemically, different codons could have been applied for alternative synthesizing pathways for the same aa: Arg AG for instance from ornithine or Pro, Ser AG from oxaloacetate via homoserine and Ile2 from Thr? Arg and Ser, AG-codons, may be seen connected via Gly (Ser → Gly, + Arg) in the creation of creatine phosphate. For Leu an alternative way exists from oxoisovalerate, a precursor to Val [14].
Alternatively, the four aas could be suspected to be a kind of ‘micro-code’ for at least three essential polarities: expressing both the polarity in valences N-O and potentially charge +/– in Arg and Ser, further the one between these more or less polar aas versus the hydrophobic Leu and Ile, and thirdly the branching ways of synthesis to different classes of substances, to keto-acids and proteins or to lipids and steroids. They are usually regarded as originating from first, middle and last stations in the glycolysis - citrate cycle.
Concerning the codons, there is no similarity in the relations between the two codons of the four ‘extras’; for Ser they are complementary, UC and AG, for Arg a change of 1st base A to C, for Leu a change C to U, and Ile2 is a special case with only a change in the 3rd base. This gives reasons to believe that the extra codons and with them the mass numbers have the function to fill out different schemes of bidirectionality of codons, AG for GA, CU for UC among mixed-encoded aas for instance, and numerical regularities in the distribution of aa masses.
The mathematical approach in this research gives the mass sum 246 of the 4 extra aas a special interest. A few different aspects are suggested here.
6.2 Numerical aspects
In the preceding article (Section 5.3.1) [8] it was shown that square roots out of 6-digit numbers from a wavy reading of the basic chain 5-4-3-2-1-0 with the superposed chain 9-7-5-3-1 gave the sum of 24 aas when starting from 5, of 20 aas when starting from 4. Outwards and inwards:
√594735 + √537495 ≈ 1504 = 24 aas
√473523 + √325374 ≈ 1258 = 20 aas
In the sum of 20 aas the first square root √473523 ≈ 688 equals the G1+A1-domains among 24 aas, and √325374 inwards ≈ 570 equals the C2+U2-domains among 24 aas.
Another aspect concerns the total sum R + B of the 4 extras = 541. This sum represented the “substituents” in the division on atom kinds when all aas were counted as uncharged, as if the 4 ‘extras’, including their B-chains, were a code for these ‘substituents’, as such a kind of “micro-code” hypothesized above.
It can be added that the total number of atoms in 20 aas is 384, 2 x 192 [12]. The addition of 4 aas = + 84 atoms, i.e. the interval 192 - 108. Thus, they fit into the scheme 12 x x2 in section 2.
In the ES-chain factor 108 was the interval 3’ → 1’, 208 – 100, divided in 49 (3’-2’) and 59 (2’-1’).
5 x 49 = 245, sum of R if Arg uncharged
5 x 59 = 295, sum of B-chains if Arg charged
A couple of other aspects concern more individual mass numbers of the 4 aas:
Firstly, transformation between nb-systems shows a relation between Arg in the H-chain and the other 3 ‘extras’ with the sum of R 145 in the L-chain:
101 in nb-10 = 145 in nb-8
Secondly, the 4 aas could possibly be seen as expressions for the spread numbers 130 of the total and 58 (here taken as the intervals 1-59 and 72-130) of the L- and H-chains, with deviations of +/– 2, this when assuming that they somehow act as a micro-code:
130, +2 = Ser2 + Arg2
2 x 58 = 116, –2 = Leu2 + Ile2
(Cf. SR-proteins in polarization of DNA-strands and Ile, Leu as alternative start codons in some organisms) [15]).
Still another kind of aspect concerns the polarity purines - pyrimidines and directions in reading of 1st and 2nd bases in codons. Domains of aas with purines and pyrimidines in steps from 1st to 2nd base implies –/+ 246, the total of the 4 ‘extras’. (Cf. numbers 688 and 570 below as square roots in the first paragraph above.)
G1 + A1 → G2 + A2 = 688 → 934 = + 246
C1 + U1 → C2 + U2 = 816 → 570 = – 246
The corresponding steps from purine to pyrimidine aa domains imply –/+ 59:
G1+A1 → C2+U2 = 688 → 570 = – 2 x 59,
C1+U1 → G2+A2 = 816 → 934 = + 2 x 59
59 equal to the spread number of L- and H-chains.
If the appearance of number 246 here have something to do with the 4 extras, it seems necessary to look at individual codons of 12 aas:
CC-CU-UC-UU = 278 5 aas
GG-GA-AG-AA = 396 7 aas ... Sum 674
Difference 2 x 59.
GC-GU-AC-AU = 292 6 aas
CG-UG-CA-UA = 538 6 aas ... Sum 830
Difference 246
(Underlined = aas in the "mixed codon" table 1 in [8]. The sums 674 and 830 equals the N-Z-division of the total –/+ 2.)
The latter codon pairs for 6 + 6 aas that defines the difference 246 is constructed by one purine and one pyrimidine, as grasping over a double strand, something that might be worth to observe. The decisive differentiating feature is that the two series represent opposite directions in reading of one strand, as “upstream” - “downstream”. A condition in this case is the suggested “two out of three” reading [16], however here not limited to translation or strong interaction in G-C-bonds [13]. It might even support the thought of an earlier 2-base code, suggested by many.
However, the number 246 here are not correlated with the separate aa masses or codons of the four “extras” and seems just as an expression for changes in directions.
The eventual relevance of these aspects must be left as an open question.
The research followed up an earlier article (doi10.1016/j.jtbi.2015.01013), of which some central findings are recapitulated in the Introduction here.
It has been found what might be the hitherto most elementary correspondence between codons and a central property of the 20 ’classical’ aas, the atomic mass. The calculations here include two sets of the four aas with two codons, thus also Ile2, AUA, giving 24 codons and numbers.
In a weight series of aas Gly to Trp the brake around Mv ∼ 63 gave two series, the L- and H-chains, showing on a ∼ 2/3-relation of mass, both in the total, in the division on atom kinds, i.e., C-atoms versus ’substituents’, and (–/+1) in codon domains of aas.
Calculating with uncharged basic aas and perhaps only Glu charged, the total of side-chains R becomes 1500 (the sum of the basic series 5 → 0 times 100). The factors 5 x 4 x 3 times the ’Pythagorean’ squares of 5, 4 and 3 were found in the divisions, the factor 5 divided 3 - 2 around Mv of an aa. The squares imply a pattern cognate with the 2x2-series behind the periodic system.
Counting on a total of 1500, divided 600 - 900 around Mv, it was further observed (Section 2.4) that transformations between nb-systems from C-skeleton parts in nb-10 to nb-8 give the correlated total and from ’substituents’ in nb-10 to nb-6 the same totals. It looks as an essential support for the hypothesis [8] that such transformations might be part of an internal reference system and here could be a stabilizing factor in the code.
These patterns seem to be a still more fundamental organization behind the structure of the code than the ES-chain, the integers 5 to 0 with exponent 2/3 times 100 [8]. Simultaneously, the same factors 192 (12 x 42) and 108 (12 x 32), with the difference 84 were found as intervals in the ES-chain: 5’ – 1’ divided 5’ – 3’ and 3’ – 1’, thus showing on a close connection.
As for the distribution of codons, it was already in the preceding paper found that A1+U1-coded aas had the same mass sum as the total sum of C-atoms and thus G1+C1-coded aas the same as the ’substituents’. The fact found here that both these codon domains of aas and the sums of atom kinds (–/+1 if counting on a total of 1500) are acted on by the 2/3-division indicates that this correlation has a deeper common arithmetical root.
The interval 5’ – 3’and 2 x 3’ in the ES-chain seems decisive, both in generating the different ’substituents’ and C-atoms after valences (Section 2.8) and in separating the complementary codon pair domains of aas, G+C versus A+U.
The types of aas showed not to be relevant in the linear order of the weight series. However, the 3/2-quotient appeared again (+/–1) when the aa side-chains were ordered in 3 groups after valences of ”characterizing” atoms: a) those with only CHx-molecules, b) those with NHx and c) those with O/S or only H molecules (Section 3.2). The groups a) + b) were equal to the H-chain in the weight series +1, group c) equal to the L-chain of this series –1. It represents a division in step 3 — 2 of the basic series when it concerns valences of C and N, 4 and 3, versus 2 and 1. (Gln and Asn here included in the group c).
The 3/2-quotient as such supports the view on such series as bidirectional, cf. figure 10b, Section 3.2. (Such a ‘head-to-head’ direction could be seen expressed in the way a sixth CO2 molecule is built in into a pentose between the opposite 3C - 2C pieces of ribulose-5-P [9]: CO2 added to the 2nd C-atom in the Calvin cycle.)
The three groups were found also to correlate with the basic series read as triplets (section 5.5 in [8]): mass sums of O/SHx + NHx equal to 2 x 543 –1, of CHx equal to 2 x 210 –1. Further, the mass relation between the O/SHx- and NHx-groups are close to the same as aas in G1+G2-domains and C1+C2-domains of aas respectively (≈ 600 and 486), similar number divisions again appearing as along different coordinate axes. All this additionally strengthens the relevance of an arithmetical interpretation of the genetic code.
Studying the spread of the weight series (Section 4) showed besides other regularities that the distances of aas from the Mv ∼ 63 summed up to exactly –/+ 2/3 of 416, i.e., 2 times 3’ in the ES-chain. In the 2x2-series (section 5.2 in [8]) the same number, 16(32 + 22) times 2/3 the factors 192 and ∼ 108 and ∼ 84 (cf. Section 2) were found again.
It was further observed that aas closest to the Mv-center, Asp and Gln, are those aas that contribute to the construction of the codon bases apart from Gly in purines, which might be regarded as representing the common B-chains.
The difference between the mass sum of the two purines G + A and the two pyrimidines C + U is 63. These facts seem to point out the Mv-break in the weight series as an essential center in the relation between coding bases and aas. It is also a geometrical relation between tetrahedrons and ring-forms (explained as a step of sp-hybridization).
The factor 192 divided 108 and 84 from section 2 are found again in the rings of complementary base pairs (as A+U or G+C): 9 C-atoms = 108 and 6 N-atoms = 84, sum 192.
Finally, some general and numerical aspects are suggested on the two sets of 4 aas with two codons.
The numerical 3/2-relations in sections 2 and 3 support the view on number 5 as a basic foundation for the different versions of the basic series 5 - 0 behind the code, (in the background model, Wohlin 2015, Section 1.2, as 5 dimensions). There is the squares of the numbers 5 - 4 - 3 (à la Pythagoras) times 3 x 4 x 5, the series of valences with 5 of phosphorus P, the 5C in riboses of nucleotides to mention a few examples.
3/2-divisions of 5 appear in several other contexts in the genetic code:
-The Z/N relation 828/676 in the total of 24 aas R ∼ √3/2.
-The opposition between 3 bonds in the G-C pair, 2 bonds in the A-U pair, “strong and weak” pairs (Rumer 1966). With reference only to sums of the 1st and 2nd bases in codons, the 5 bonds in mixed-coded aas can be seen as polarized –/+1, giving 4 bonds in the A+U-group, 6 in the G+C-group of non-mixed aas.
-The number of bases, 3 from the parent orotate (U+C+T) and 2 from inosine (A+G), the sums of which also are each other’s inversions, (349 and 286 with the difference equal to Mv of aas ∼ 63.
-The “2- to 3-base-coded” aas, not concerning mass but number of relevant bases in codons.
-There is also the division of valence 5 of phosphorus P in nucleotides into 3/2!
In pure mathematics 5 happens to be the sum of the preceding primes 3 and 2 in the Fibonacci series. However, the whole series of valences 5-1 seems more relevant biochemically with the distinguishing nitrogen in the code and in proteins: the polarity 3 — 2 in valences of N and O as essential for peptide bonds for instance. With charges it is possible to describe as steps (4←3) and (2→1), activating a deeper level of polarization of 5, 4 ←→ 1, the C-H-level.
Another example of 3/2-relations can be found in the Z-sums of NADP and ATP, evaluated as circa 3/2 in energy supply. The numbers are also close to inversions of each other (x10x), which might be seen as an expression for the bidirectionality of series and processes:
Z NADP to NADPH (+H) = 385 - 387, Z ATP =256 - 260 charged to uncharged. There are intermediate Z-numbers that both are related 3/2 and as inversions of each other:
387 = 3/2 x 258,
385 /\ = ∼ 260. x 10-5,
Cf. √15 = 387.3. x10-2, /\ = 258.2. x 10-3, 15 the sum of the basic series 5 - 0 and the Z-number of phosphorus P.
The quotient between triplets in the basic series gave similar numbers: 543/210 = 258.57 x10-2, /\ = 386.74 x 10-3. the quotient 2.58... the same as between aas with NHx- and O/SHx-groups versus non-polar aas with only CHx-groups.
The mass relation between the opposite ends of B-chains of aas COO- and NH3+ = 44/17 shows up to give a similar quotient = 386.36. x 10-3, /\ 258.82. x 10-2.
Further, the numbers 387 and 258 are 3 and 2 times the number 129, the interval Gly → Trp in the weight series; 129 circa half of 2’ + 1’ = 259 in the ES-series.
The C-skeleton in the weight series (Section 2) with the highest capacity for net-working and the total mass exactly 3 and 2 times 192 in R appears naturally decisive as a bottom layer. Another example of its role might be seen in the number of all atoms in R-chains: exactly twice the total number of C-atoms in R+B-chains, 256 to 128. So too in G1+C1-domains: 47 C in R+B, 2 x 47 atoms in R, and in A1+U1-domains: 81 C in R+B, 2 x 81 atoms in R. (Cf. the duplicated representation of the human body in our cerebral cortex!)
As said above, an evolution along the weight series is only partially possible to imagine. It seems necessary to count on a two-way direction in the numeral series as a fundamental feature. Yet, one fact at least could indicate that the liner order of masses at some stage in the construction had relevance: that the stop-codons follow as variations of codons for the two heaviest aas.
The L- and H-chains of the weight series are only one of many polarities, this word taken in a wide sense. A suggestion is to sooner imagine such polarizations as representing different diagonals in a circle of smaller or wider size, and processes as along a ‘vertical’ axis through the origin up - down between different levels and dimensional geometries. The evolution could perhaps be described in terms of an early adaptation to such numerical/geometrical grids along different coordinate axes.
Generally, the found relations strongly reinforce the main hypothesis of numeral schemes in a self-organization of the genetic code and its mass distribution, contradicting the ”frozen accident” hypothesis [1].
How such numerical series could have organized the code is hardly more curious than the construction of atoms and their electronic shells. Very hypothetically one part of the answer may hide in the since long used mass spectrometer, other parts in deeper studies of M-fields, the quantization of magnetic flux appearing in superconductors and such things, certainly left here to the specialists. (M-fields connected with mass as sons - or grandsons - of Gravity with big G?)
The author want to thank the anonymous reviewers of the preceding article for their viewpoints, not least for their references to articles from the 1980th. Special thanks are addressed to M. Di Giulio, whose interesting idea 1989 inspired this follow-up research.
View supplementary data 1
View supplementary data 2
- Crick FH (1968) The origin of the genetic code. J Mol Biol 38: 367-379. [Crossref]
- Shcherbak V (1993) Twenty canonical amino acids of the genetic code: the arithmetical regularities. Part I. J Theor Biol 162: 399-401. [Crossref]
- Shcherbak VI (1994) Sixty-four triplets and 20 canonical amino acids of the genetic code: the arithmetical regularities. Part II. J Theor Biol 166: 475-477. [Crossref]
- shCherbak VI (2003) Arithmetic inside the universal genetic code. Biosystems 70: 187-209. [Crossref]
- Downes AM, Richardson BJ (2002) Relationships between genomic base content and distribution of mass in coded proteins. J Mol Evol 55: 476-490. [Crossref]
- Racocevic MM (2004) A harmonic structure of the genetic code. J Theor Biol 229: 221-234. [Crossref]
- Perez JC (2015) Deciphering Hidden DNA Meta-Codes -The Great Unification & Master Code of Biology. J Glycomics Lipidomics 5: 131.
- Wohlin Å (2015) Numeral series hidden in the distribution of atomic mass of amino acids to codon domains in the genetic code. J Theor Biol 369: 95-109. [Crossref]
- Karlson P (1976) Biokemi (Biochemistry). Libers Läromedel Lund.
- Gell-Mann M, Ne’eman Y (1964) The Eightfold Way. Benjamin WA, Inc. New York, Amsterdam.
- Di Giulio M (1989) Some aspects of the organization and evolution of the genetic code. J Mol Evol 29: 191-201. [Crossref]
- Négadi T. (2011). The multiplet structure of the genetic code, from one and small number.
- [arxiv.org/pdf/1101.2983].
- Rumer YuB (1966) [Codon systematization in the genetic code]. Dokl Akad Nauk SSSR 167: 1393-1394. [Crossref]
- Nicholson, D.E. (1976). Metabolic Pathways. Koch-Light Laboratories LTD, Coinbrook, Bucks, England.
- NCBI, Taxonomy (2013). [http://www.ncbi.nlm.nih.gov/Taxonomy/taxonomyhome.html/index.cgi?chapter=tgencodes]
- Lagerkvist U (1978) "Two out of three": an alternative method for codon reading. Proc Natl Acad Sci U S A 75: 1759-1762. [Crossref]











