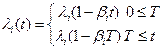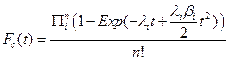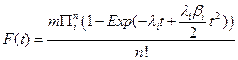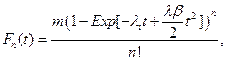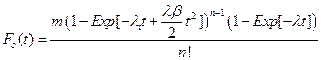Abstract
In this paper we explore the implications of two models of carcinogenesis on the incidence of cancer in extreme old age (80 years or older). Both models pose that cancer is the final stage of a multistage process and that the transition rates between stages slows with age. We find that in a 7-stage model, where all stages have monotonic transition rates, a decrease of as little as 60% in the transition rate of each stage could cause the observed decrease in cancer risk at extreme old age. If only the transition rate of a single stage slows, then a decrease of at least 90% is needed to explain the observed patterns of cancer incidence. Because of this, we conclude that it is likely that if a decrease in transition rates is indeed responsible for the decrease in cancer incidence risk at extreme old age then multiple stages are involved.
Introduction
The multistage model of carcinogenic has been a cornerstone of the mathematical study of cancer incidence since it was first proposed by Armitage et al. [1]. This model proposes that cancer is the final stage of an n-stage evolutionary process. The beauty of this model is that despite its conceptual simplicity, variations of it have been able to describe several patterns of cancer incidence that seem to prevail across time and geography [2]. Specifically, this model was created to explain the prevalence of a power law in cancer incidence across several types of cancer. However, one pattern which seems to prevail almost universally across cancer incidence functions is not explained by the simple model of Armitage et al. [1].That is a leveling off, and in several cases, a decrease in extreme old age (after age 80) [3, 4].
To explain these phenomena at least two coherent theories have been proposed and explored: statistical under-reporting [5] and cellular senescence [2]. However, one recent theory which varies substantially from these is that the transition rates from one stage to another slow down with age [2]. The justification for this theory lies in the fact that many biological processes which are necessary for the development of a malignant tumor tend to slow down or lose efficiency with age [6]. Thus a sufficient slow down of one or more stages might cause a corresponding decrease in the number of new cases of cancer. In essence cells would become ”stuck” in precancerous stages. However, this fairly intuitive idea raises two questions: how many stages would have to be affected, and how much of a slowdown would be needed for each stage?
In this note we explore these questions through two models, which we will call ODS and NDS, each of which is a variation of a compound Poisson process used to model the multi-stage carcinogenesis theory. In the next section, we describe these models in detail. In Section 3 we present our study design to find biologically feasible parameter ranges, and in Section 4 we present and analyze our findings.
Model description
The two models explored in this paper are specific examples of a general model which assumes the following:
- cancer occurs as the final mutation of an ordered n−mutation process,
- mutations are independent events,
- transitioning to the ith mutation is a time-in homogenious Poisson process with intensity
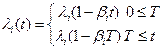
where t is time, T ≥ 90, λi is the initial transition rate for the ith mutation,
βi is the annual rate of decrease for the transition rate λi and βi < 1/T,
The probability of developing cancer in any two susceptible cells is independent events.
Using these assumptions, we construct the cumulative distribution function for a single cell explicitly for t £ T as:
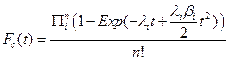
Thus, if we have a large number of susceptible cells in a tissue, m, and cancer is a sufficiently rare event then the cumulative distribution function for a tissue approximates the following relationship:
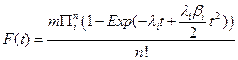
The special case where λi = λ > 0 and βi = β > 0 for all i, was briefly examined in [7]. We will denote this particular case of the general model as the n−decreasing stage model (NDS). One interesting property of the NDS is that the Taylor expansion of the corresponding probability density function gives a truncation mathematically equivalent to the model of [2], which in turn was based on the assumption of cellular senescence. Thus NDS allows for an alternative biological explanation for the model of [2]. In this paper, we will contrast the NDS model with a one stage decreasing model (ODS). For ODS we assume λi = λ > 0, and that for one particular value of j, βj > 0 and for i ≠ j that βi = 0.
Given the above assumptions we find that for NDS the cumulative distribution function become,
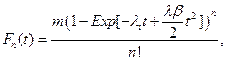
and for ODS,
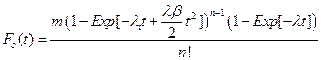
From these two equations, we determine the probability density function of each model as: fn(t) = Fn'(t) and fo(t) = Fo' (t). We will use the probability density function as a proxy for cancer incidence, thus In(t) = fn(t), and Io(t) = fo(t).
Study design
For the purpose of this study, we followed the original conclusions of [5,1], that is, n = 7 (this is necessary to explain the 6th degree power law observed in several cancers, including lung cancer). We selected time points at years t 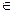 {2.5, 7.5, 12.5, ..., 87.7, 90} (these particular values are the same as those used to censor actual incidence data in [6,8]) for a total of 19 points. For both models, we first found biologically feasible values of λ by setting β = 0 and deeming a value of λ feasible if the correlation between log(I(t)) and log(t) was at least 0.95 (noting that in the case that β = 0 Io(t) = In(t) = I(t)).
{2.5, 7.5, 12.5, ..., 87.7, 90} (these particular values are the same as those used to censor actual incidence data in [6,8]) for a total of 19 points. For both models, we first found biologically feasible values of λ by setting β = 0 and deeming a value of λ feasible if the correlation between log(I(t)) and log(t) was at least 0.95 (noting that in the case that β = 0 Io(t) = In(t) = I(t)).
Once the possible range of λ was determined, we subdivided the range from λ = 0 to λ = 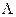 , with
, with 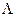 being the maximum biologically feasible value found, into steps of size 0.001. For the ith step, we defined βimin(A) to be the value of β which caused a peak at age 85 and βimax(A) to be the value of beta which causes a turnaround at age 75 for model A
being the maximum biologically feasible value found, into steps of size 0.001. For the ith step, we defined βimin(A) to be the value of β which caused a peak at age 85 and βimax(A) to be the value of beta which causes a turnaround at age 75 for model A 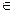 {ODS, NDS}. Having completed this calculation, we found the cumulative percentage decrease from birth to age 90 for each combination of λi and βi, for all i.
{ODS, NDS}. Having completed this calculation, we found the cumulative percentage decrease from birth to age 90 for each combination of λi and βi, for all i.
Analysis of parameter values
The biologically feasible combinations of parameters along with the cumulative slow down of transition rates are summarized in Figure 1.
Figure 1. Study Results
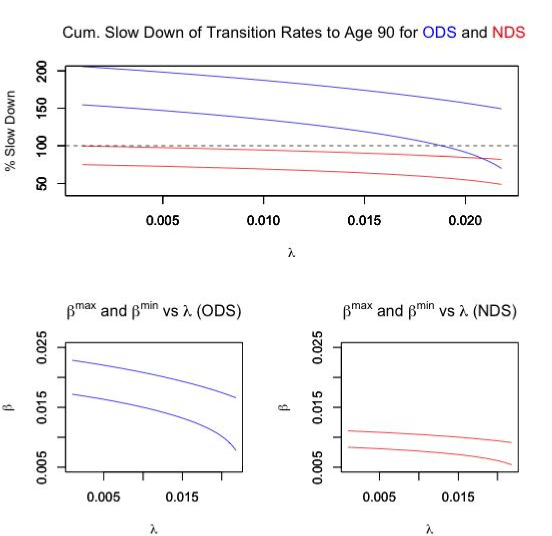
Of course, a cumulative slow down in excess of 100% would not be biologically possible, thus we can conclude that the ODS model could only cause a turnaround after age 80. Since this is later then is typically observed [3,4,7], we conclude that the ODS is a poor model to explain actual cancer incidence data. However, for the NDS, we see that for the entire range of λ, we can find values of β which may in fact be biologically possible. Thus, it seems likely that if a slow downs of transition rates is responsible for the turnaround at old age, then multiple stages would have to be involved.
References
- Armitage P, Doll R (1954) The Age Distribution of Cancer and a Multi-stage Theory of Car-cinogenesis. Brit J Cancer 8: 1–12. [Crossref]
- Hiller J, Vallejo C, Betthauser L, Keesling J (2016) Characteristic patterns of cancer incidence: Epidemiological data, biological theories, and multistage models. Preprint.
- Pompei F, Polkanov M, Wilson R (2001) Age Distribution of Cancer: The Incidence Turnover at Old Age. Toxicol Ind Health 7: 1619–1650. [Crossref]
- Ritter G, Wilson R, Pompei F, Burmistrov D (2003) The mul-tistage model of cancer development: some implications. Toxicol Ind Health 19: 125–145. [Crossref]
- Nording CO (1951) A New Theory on the Cancer-inducing Mechanism. Brit J Cancer 7: 68–72. [Crossref]
- Yun MH (2015) Changes in Regenerative Capacity through Lifespan. Int J Mol Sci 16: 25392-25432. [Crossref]
- Gerstung M, Eriksson N, Lin J, Vogelstein B, Beerenwinkel N (2011) The temporal order of genetic and pathway alterations in tumorigenesis. PLoS One 6: e27136. [Crossref]
- Knudson AG Jr (1971) Mutation and cancer: statistical study of retinoblastoma. Proc Natl Acad Sci U S A 68: 820-823. [Crossref]