Take a look at the Recent articles

Abstract

Low temperature is associated with a large increase in the risk of unexpected sudden cardiac death. The effect of cold exposure on the incidence of ischemic heart disease (IHD) is well documented. However, the effect of other meteorological factors, such as relative humidity, has not yet been affirmed or declared. This study aims to assess the effects of the change in mean temperature and relative humidity on the onset of IHD by estimating the trend towards the risk of incidence. As humidity is closely related to the inflammatory system, we further clarified the underlying mechanism that connects weather and disease from the perspective of the inflammatory network. Whereas most epidemiological studies employed the usual regression models, we used a naive Bayes classifier for the data of patients. By applying a naive Bayes classifier, we developed a new method to capture the trend of the change in meteorological factors leading to the onset of IHD. We identified general patterns of tendencies of weather factors (mean temperature and relative humidity) that led to the onset of IHD. These findings suggested the cytokine network, including various interleukins and especially interleukin-6 as a key cytokine, as a mechanism connecting weather and IHD. Avoiding the incidence of IHD has become an important issue of public health care. Our findings are expected to contribute to predicting and preventing the onset of IHD through daily weather observation.

Key words

cytokine, cardiovascular, coronary, weather, interleukin, humidity

Introduction

The incidence of ischemic heart disease (IHD) is known to have the tendency of being high in days of low temperature [1]. Cold exposure is associated with a large increase in the risk of unexpected sudden cardiac death [2]. However, the relation of heart disease to other meteorological factors (e.g. humidity), has remained unclear. Some studies reported no evidence of a humidity effect on the onset of diseases [3]. Nevertheless, rainfall was found to be related to variations in IHD mortality [4]. The combination of rain and snow could produce a dramatic increase in mortality from cardiovascular disease [5]. These findings suggest that high relative humidity could be connected with the incidence of IHD.

Recently, the combination of decreased barometric pressure and increased temperature was reported to lead to a high risk of heart disease even in winter seasons [6]. An increase in relative humidity was observed at the same time. The relation of heart disease and humidity was also studied in connection with air pollution. A dew point association was observed for coronary atherosclerosis and congestive heart failure [7]. Note that a high dew point temperature usually means high relative humidity. Relative humidity resulted in a high inflammatory index, such as CRC values [8]. An increase in dew point temperature was associated with an increase in risk of hospitalisation for coronary atherosclerosis and for congestive heart failure [7].

We applied a naive Bayes classifier to capture the overall tendency of weather factors that could lead to the incidence of IHD. A naive Bayes classifier is originally known as a method for discrimination. The present work provided a new aspect of application of the naive Bayes method. The ‘tendency of weather factors that could lead to the incidence’ was expressed as a vector, ‘risk direction’, in the plane of two variables, namely, mean temperature and relative humidity. We explored the patterns of these vectors of ‘risk directions’.

These findings on the patterns of risk vectors suggest that relative humidity plays an important role in the inflammatory response system of humans. This study suggests a possible mechanism for the incidence of IHD in connection with a cytokine network that mediates the inflammatory response.

Method

The data comprised the daily number of patients and the meteorological observations. We used the daily data of the number of IHD patients during two periods: 2002–2005 and 2009–2012. The data were provided by the city of Nagoya in Japan. Nagoya has a standard subtropical climate with four characteristic annual seasons, and its climate is characterised by the development of one month of rainy period. The data of patients, regardless of age, who were first transported by ambulance to a hospital and then diagnosed at the hospital with myocardial infarction or angina pectoris, were included. The daily meteorological data, including mean temperature, barometric pressure and relative humidity, were extracted from the Japan Meteorological Agency.

We developed a new method to capture the directional vectors of meteorological observations, along which the risk of IHD increased. Our method is based on a naive Bayes classifier known as a Bayesian network. A naive Bayes classifier is originally a method for classifying or distinguishing several categories.

A naive Bayes classifier is a simple probabilistic method based on the application of Bayes' theorem with an independence assumption of variables [9-11]. Let X=(X₁, . . . , X_n) be an array of random variables denoting the observed attribute values (e.g. mean temperature or relative humidity) and C be the random variable denoting the class of an instance (e.g. high risk or low risk). Let c be a particular class label and x=(x₁,...,x_n) represent a particular observed attribute value. To simplify the calculation, we need the following independence assumption: attributes X₁, . . . , X_n are all conditionally independent of each other given C. This assumption dramatically simplifies the representation of the conditional probability P(X | C) and the problem of estimating it from the training data.

Given the vector of observed values for the predictive attributes X=(X₁, . . . , X_n), the probability P(C | X) of a class C can be calculated using the Bayes' theorem:

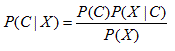
As the attributes are assumed conditionally independent, the following equation holds:

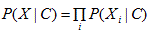
Therefore, we obtain the following:

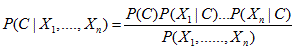
In this work, we set n=2 and X as a pair of meteorological factors. The variable X₁ and X₂ are set to the daily data on mean temperature and relative humidity, respectively. The variable is C expressed as a risk for IHD and is defined as a set of two classes of ‘high’ risk and ‘low’ risk for IHD. The above equation means that if we are given the mean temperature and the relative humidity of a certain day, then the probability of the onset of the IHD can be forecast by calculation according to the above equation.

Results

We apply a naive Bayes classifier to the data on meteorological factors and IHD patients in Nagoya. A naive Bayes classifier can be considered as a simple case of Bayesian network with arrows from one class variable C to several observed variables X₁, . . . , X_n:

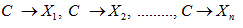
The purpose of a naive Bayes classifier is to estimate the class of C from the given observed data X₁,….,X_n, using Bayes' theorem [9-11].

We define the observed variables and the class variable as a naive Bayes framework as follows. The daily data on the mean temperature and the relative humidity in Nagoya are obtained from the Japan Meteorological Agency. We define an observed variable X₁ as the mean temperature and X₂ as the relative humidity:

By combining these variables, we have X=(X₁, X₂). The daily data on the number of IHD patients are provided by the city of Nagoya. We divide the number of patients into three classes, namely, ‘high risk’, ‘moderate risk’ and ‘low risk’, with high (or low) risk cases occupying 30% of the total number of cases. As we are interested in extreme cases, we select only the high and low cases. Thus, we define class variable c₁ as ‘high risk’ and c₂ as ‘low risk’

The class variable is defined as C={c₁, c₂}. The purpose of a naive Bayes classifier is to estimate whether the day is ‘high risk’ (C = c₁) or not for the onset of IHD from the given observed data on the mean temperature (X₁= x₁) and relative humidity (X₂= x₂). A naive Bayes classifier answers this question by providing the probability that the risk becomes ‘high’.

The calculation of a naive Bayes is performed over lattices in the plane X=(X₁, X₂). The observed data on the mean temperature and relative humidity x=(x₁, x₂) on a certain day can be considered as a point in the plane X=(X₁, X₂). Class C (high risk or low risk) on the same day is regarded as a type of value over the point x=(x₁, x₂) by assigning the value of 1 to ‘high risk’ and 0 to ‘low risk’. These values over the points are called training data or teacher signals. By selecting arbitrary 10 values from the interval [min(X₁)_, max(X₁)] and another 10 values from [min(X₂)_, max(X₂)], we construct 10×10 lattices L in the plane X=(X₁, X₂) formed by crossing these 10 values on each variable X₁ and X₂.

A naive Bayes classifier is a method that provides an ‘extension’ of the training data to the whole lattices L by assigning decimals in the interval [0,1]. Given a point x in lattice L, a naive Bayes classifier calculates the probability that the risk for IHD becomes ‘high’ at that point (x₁, x₂) by applying Bayes’ theorem. Gathering all these values over the whole lattices L, we can obtain a function over the lattice. This function is considered as the distribution of probabilities (probability distribution) over L. If we treat this function over the lattice like a function over the plane, the tilts of the function can be calculated approximately. These tilts are called gradient vectors that express the directions along which the risk for IHD increases the most. Therefore, these gradient vectors can be called ‘risk direction’ because the vectors show a ‘tendency towards high risk’.

The stochastic significance of this method is determined by calculating the forecasting rates. By comparing the observed data with the result of the naive Bayes classifier, we can check how many risky days are estimated as very ‘risky’ by the naive Bayes method. Counting the hitting cases and dividing them by the total number of observations gives a number between 0 and 1, which is the score of the forecasting rates.

We calculate all the ‘risk directions’ for the periods in the winter seasons (i.e. December, January and February) during two terms, 2002–2005 and 2009–2012, respectively. Exploring all these risk directions, we list the cases of high scores of forecasting rates (greater than 0.7) in Figure 1.

In Figure 1, the scores of forecasting rates are 0.75 in 2003, 0.68 in 2004, 0.70 in 2009 and 0.73 in 2010.

By observing the vectors of directions in Figure 1, we can capture an overall trend towards high risk when the mean temperature and the relative humidity change. We find the following main patterns of risk directions:

(a) If the mean temperature decreases and the relative humidity increases at the same time, then the risk of IHD will increase.

(b) If the mean temperature increases and the relative humidity increases at the same time, then the risk of IHD will increase.

These two patters are observed at the same time for the winter seasons in 2003, 2004 and 2010. In 2009, the trend is mostly observed for the mean temperature. If the mean temperature decreases, then the risk will increase (i.e. the so-called ‘cold exposure’). However, even in this case, a slight increase in relative humidity is observed for relatively cold days.

Therefore, the patterns in Figure 1 can be interpreted as indications of the role of relative humidity. The increase in relative humidity is closely related to the change in risk towards the risky state of IHD. This observation suggests the existence of an inflammatory response in the background of the incidence of IHD. As an inflammatory response is mediated by the cytokine network including various interleukins, the role of relative humidity is considered further in this direction in the discussion section.

Discussion

By applying a naive Bayes classifier to the data on IHD patients, we calculate the probability of the incidence of the disease for given data of mean temperature and relative humidity.

The collection of this probability gave us a distribution function over the plane of two variable parameters, namely, mean temperature and relative humidity. By calculating the gradient vectors of this probability distribution, we obtain a collection of vectors expressing the directions along which the risk of IHD increases. Therefore, these vectors are called risk direction. These risk directions for the winter seasons in two terms, 2002–2005 and 2009–2012, are explored. The results of the high scores of forecasting are described Figure 1.

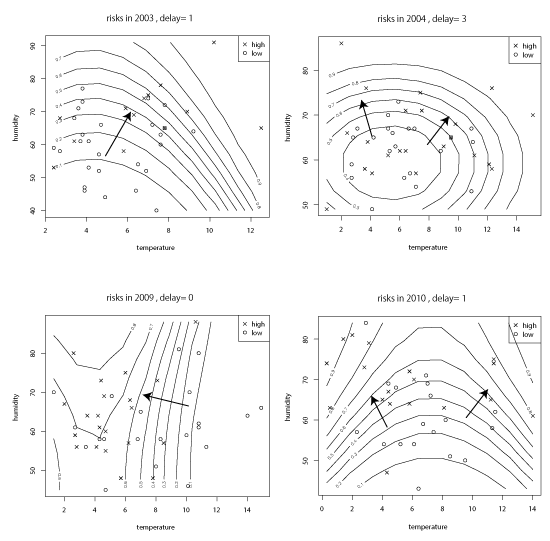
Figure 1. Risk vectors of ischemic heart disease [Notes: The horizontal lines indicate the mean temperature, and the vertical line indicates the relative humidity. The curves are the contour curves of the same probability that the risk of the pair (x₁, x₂) becomes high. The vectors are the ‘risk direction’, i.e. the direction along which the risk increases. Only the cases of high scores (> about 0.7) are extracted.]

Cold exposure has been known as a trigger of IHD. However, we observe that relative humidity also plays also an important role, especially in warm cases in winter. Relative humidity is known to increase the expression of intercellular adhesion molecule 1 (ICAM-1) in warm and humid days [12]. ICAM-1 is a protein that is typically expressed in endothelial cells and functions as an ICAM, which leads to the formation of plaque, arteriosclerosis and the incidence of IHD. Therefore, the immune system can be considered as a bridge that connects the weather and the incidence of IHD.

This observation suggests the role of the immune system through the cytokine network, which connects the weather and the incidence of diseases. In Figure 2, the relationships between the weather and the cytokine network are described in connection with the metabolic syndrome as a basic parameter.

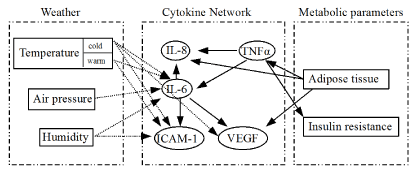
Figure 2. Weather and cytokine network [Note: The figure comprises three boxes: ‘Weather’, ‘Cytokine Network’ and ‘Metabolic parameters’. ‘Weather’ contains the meteorological factors, ‘Cytokine Network’ incorporates the various interleukins and ‘Metabolic parameters’ implies the rate of progress of the metabolic state, which is characterised by insulin resistance and the amount of adipose tissues. Both vascular endothelial growth factor (VEGF) and intercellular adhesion molecule 1(ICAM-1) in the ‘Cytokine Network’ may be a source of IHD.]

Figure 2 shows that the cytokine network is a bridge that connects the other two boxes. Obese individuals express more tumour necrosis factor alpha (TNF-alpha) mRNA and protein in fat tissue relative to the lean controls [13,14]. TNF-alpha then induces insulin resistance [14]. TNF-alpha plays a central role in inflammation. The increase in TNF-alpha induces interleukin-8 (IL-8) and interleukin-6 (IL-6) gene expressions [15]. IL-6 stimulation induces IL-8, ICAM-1 and VEGF expressions [15].

Several reports have identified the effect of weather on cytokines. Significant increases in the concentration of IL-6 were observed after cold exposure [16]. Temperature or relative humidity levels were associated with the methylation of intercellular adhesion molecule 1, ICAM-1 [12]. An increase in VEGF was observed in cold-induced angiogenesis in adipose tissues [17]. Hydrostatic pressure induced the expression of IL-6 and TNF-alpha mRNAs in a chondrocyte-like cell line [18]. The increase in IL-6 and ICAM-1 was considered as the effect of relative humidity [8]. The increase in dew point temperature (i.e. the increase in relative humidity) was associated with the increase in the risk of hospitalisation for coronary atherosclerosis and congestive heart failure [7].

ICAM-1 is an adhesion molecule that mediates the contact between circulating leukocytes and endothelial cells. ICAM-1 induces a tight binding of leukocytes to the endothelium. In this way, leukocytes can leave the bloodstream and enter the subendothelial space. VEGF induces angiogenesis. The overexpression of VEGF is a contributing factor to the development of disease. The overexpression of VEGF can lead to vascular disease in the retina and other body parts. Therefore, both VEGF and ICAM-1 may be a source of IHD.

As an increase in IL-6 and ICAM-1 was observed as an effect of relative humidity and warm temperature [12], this finding corresponds with our results with respect to the trends of mean temperature and relative humidity towards risk of IHD. Figure 2 shows that all of the meteorological factors induce the expression of IL-6. Therefore, IL-6 plays a key role in the cytokine network connecting the weather and the onset of IHD.

Possible mechanisms

Our findings suggest the following mechanistic hypotheses (Figure 2):

A metabolic life leads to an increase in adipose tissues and a release in TNF-alpha, thus causing insulin resistance. The increase in TNF-alpha induces pro-inflammatory cytokines IL-6 and IL-8.

An increased production of IL-6 activates the release of VEGF and ICAM-1. This activation forms a basic background that may lead to IHD. IL-6 may be a marker of this progress.

Weather factors (tempe2021 Copyright OAT. All rights reservive humidity) cause an increased release of IL-6, VEGF and ICAM-1. An enhanced acute-phase response due to this effect by the weather may increase pro-coagulant activity and endothelial cell activation, and it may result in an increase in coagulation proteins or the evidence of activation of the clotting cascade.

These changes in blood parameters, together with plaque instability, may ultimately lead to the onset of IHD in susceptible patients.

Conclusion

We find general trends of meteorological factors that may lead to an increase in the risk of IHD. Relative humidity shows a characteristic tendency associated with high risk. These findings suggest the importance of a cytokine network as a bridge that connects the weather and the daily life of metabolism, thus leading to the onset of IHD. Elevated levels of IL-6 are found to be associated with both weather and metabolism. Our findings imply that the cytokine network may be a good marker for determining the possible risk of future fatal and nonfatal IHD. 

References

1. Donaldson GC, Keatinge WR (1966) Early increases in ischaemic heart disease mortality dissociated from and later changes associated with respiratory mortality after cold weather in south east England. J Epidemiol Community Health 51: 643-648.
2. Gerber Y, Jacobsen SJ, Killian JM, Weston SA, Roger VL (2006) Seasonality and Daily Weather Conditions in Relation to Myocardial Infarction and Sudden Cardiac Death in Olmsted County, Minnesota, 1979 to 2002. J Am Coll Cardiol 48: 287-292.
3. Schwartz J, Samet JM, Patz JA (2004) Hospital Admissions for Heart Disease. Epidemiology 15: 755-761. [Crossref]
4. West RR, Lloyd S, Roberts CJ (1973) Mortality from ischaemic heart disease--association with weather. Br J Prev Soc Med 27: 36-40. [Crossref]
5. Baker-Blocker A (1982) Winter weather and cardiovascular mortality in Minneapolis-St.Paul. Am J Public Health 72: 261-265. [Crossref]
6. Morimoto H (2016) Association Analysis Identifies Risk of Ischemic Heart Disease When Temperature Increases. Int J Soc Sci Stud 4: 55-62.
7. Koken PJM, Piver WT, Ye F, Elixhauser A, Olsen LM, et al. (2003) Temperature, Air Pollution, and Hospitalization for Cardiovascular Diseases among Elderly People in Denver. Environ Health Perspect 111: 1312-1317. [Crossref]
8. Rückerl R, Ibald-Mulli A, Koenig W, Schneider A, Woelke G (2006) Air Pollution and Markers of inflammation and coagulation in patients with coronary heart disease. Am J Respir Crit Care Med 173: 432-441. [Crossref]
9. Albert JH, Chi S (1993) Bayesian Analysis of Binary and Polychotomous Response Data. J Am Stat Assoc 88: 669-679.
10. Soria D, Garibaldi JM, Ambrogi F, Biganzoli EM, Ellis IO (2011) A ‘non-parametric’ version of the naive Bayes classifier. Knowledge-Based Systems 24: 775-784.
11. Morimoto H (2017) A probabilistic approach for links between rheumatic diseases and weather. Internal Medicine and Care 1: 1-4.
12. Bind MA, Zanobetti A, Gasparrini A, Peters A, Coull B, et al. (2014) Effects of temperature and relative humidity on DNA methylation. Epidemiology 25: 561-569. [Crossref] 
13. Lubberts E (2008) IL-17/Th17 targeting: on the road to prevent chronic destructive arthritis? Cytokine 41: 84-91. [Crossref] 
14. Hotamisligil GS, Arner P, Caro JF, Atkinson RL, Spiegelman BM (1995) Increased adipose tissue expression of tumor necrosis factor-alpha in human obesity and insulin Resistance. J Clin Invest 95: 2409-2415. [Crossref]
15. Pang G, Couch L, Battey R, Clancy R, Cripps A (1994) GM-CSF, IL-1 alpha,IL-1 beta,IL-6,IL-8,IL-10,ICAM-1 and VCAM-1 gene expression and cytokine production in human duodenal fibroblasts stimulated with lipopolysaccharide, IL-l alpha and TNF-alpha. Clin Exp Immunol 96: 437-443. [Crossref]
16. Hoffman HM, Rosengren S, Boyle DL, Cho JY, Nayar J, et al. (2004) Prevention of cold-associated acute inflammation in familial cold autoinflammatory syndrome by interleukin-1 receptor antagonist. The Lancet 364: 1779-1785. [Crossref]
17. Xue Y, Petrovic N, Cao R, Larsson O, Lim S, et al. (2009) Hypoxia-Independent Angiogenesis in Adipose Tissues during Cold Acclimation. Cell Metabolism 9: 99-109. [Crossref]
18. Takahashi K, Kubo T, Arai Y, Kitajima I, Takigawa M, et al. (1988) Hydrostatic pressure induces expression of interleukin 6 and tumour necrosis factor ?? mRNAs in a chondrocyte-like cell line. Ann Rheum Dis 57: 23-236. [Crossref]