Take a look at the Recent articles

Summary

Tissues belonging to cardiovascular system show a viscoelastic behavior, due to superposition of an elastic and a viscous component, so that, the transmission of mechanical energy across the system is split in two parts: one can be stored into tissues and can be retrieved due to elasticity, while the second part is dissipated due to viscosity.

This paper aims at an introductory explanation of the possibilities offered by the fractional calculus in the analysis of the viscoelastic behavior of cardiovascular system.

Viscoelasticity of arteries

Arteries show a viscoelastic behavior, so that energy transmitted is both stored and dissipated due to elastic and viscous components of arterial walls [1-7]. The knowledge of that behavior and the knowledge of the elastic and viscous components may be of paramount importance in the study of physiopathological mechanisms of degenerative disease affecting cardiovascular systems.

The first relevant studies published about this topic examined the static and dynamic viscoelastic behavior of the dog’s arteries [1,2] published a milestone study examining the viscoelasticity of the dog’s arteries by means of the analysis of the correlation between radius and pressure at various frequencies. He observed a significant increase in the value of the dynamic elastic (Young’s) modulus based on the frequency of the pulse wave, and on the muscular component of the arterial wall. In particular, since the Young’s modulus is given as [3]:

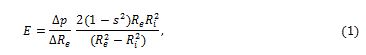
where 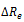is the variation of external radius induced by the pressure variation 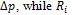is the internal radius, and  is the Poisson’s ratio, e.g. the ratio of the transverse to the axial strain. The Young’s modulus of equation (1) may be split into an elastic and a viscous component [2], respectively E_c and E_s, given by

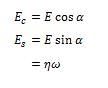
α being the phase between pressure change and external radius dilatation, ηthe viscosity, and ωthe pulsation, e.g., 2π times the frequency. ν

Simulation of the mechanical behavior of arteries is performed using mathematical modeling involving springs (representing elasticity) and dashpots (representing viscosity) in series and in parallel. In a spring, the relationship between stress σ and strain ε is given by the equation

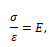
while in a dashpot the relationship is

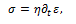
the symbol 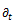denoting the time derivative. The main combinations of spring and dashpot are the Maxwell model (a spring and a dashpot in series) and the Voigt model (a spring and a dashpot in parallel) [5].

The Maxwell model, with spring S and dashpot D in series is characterized by a total stress equal to the stress in both elements, which must be the same, so that 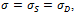, while total strain is given by the sum of individual strains, to get 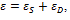, and the time variation of the strain is

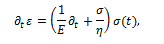
being of course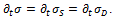

In the Voigt model, instead, total stress is given by the sum of the individual ones, e.g., 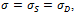and a total strain is 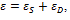so that the stress can be written in the form:

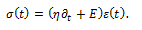
A further model, called the standard linear solid (SLS) model [6], combines a Maxwell model with a spring in parallel. If the Young’s modulus of the spring in parallel is E_p, and the Yong’s modulus of the spring in the Maxwell model is E_M, then the equation governing the standard linear solid model is

Fractional calculus

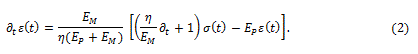
Fractional calculus is a branch of mathematical analysis which studies the fractional derivation and integration of given functions. In first approximation, it can be used when two or more physical effects are superposing and therefore, both are to be taken into accounts.

A simple way to explain how fractional calculus [8] may arise can be evolved knowing that the n-th derivative of a function

 

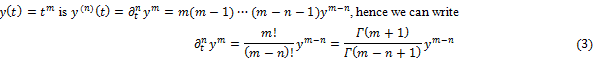
where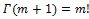 is the Euler Gamma function, m! denoting the factorial of m, e.g., the product m(m –1) ...1. We can then infer

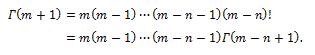
Indeed, the Gamma function is a generalization of the factorial, and is defined for any possible value of a complex variable z, based on its definition

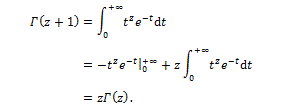
Starting from these premises, the Swiss mathematician Leonhard Euler, in 1730 noted that the definition in equation (3) allows to calculate a derivative of fractional order. Using the value 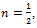Euler obtained

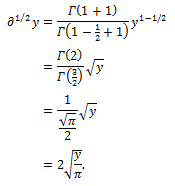
Using the same Euler’s procedure, one may then calculate a derivative of any order, like for example, the derivative of y^π of order e, as follows

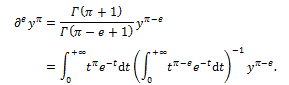
More generally, we can use the definition of fractional derivative of order α of a function due to Riemann-Liouville as

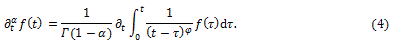
The same reasoning may lead to definition of integrals of non-integer order, since – based on the Riemann-Liouville definition of n-th order integration – we can write, for an integer n and for an integrable function: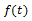

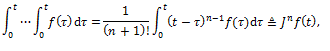
and generalizing the integral to a fractional order φ we obtain:

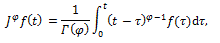
which allows us to integrate 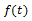a non-integer number of times [8-10].

Applications of fractional calculus for the study of viscoelasticity of arteries

The analysis of viscoelastic behavior of bodies by means of the fractional calculus starts from the possibility to define the fractional derivative of strain, from which one gets the stress in the equivalent forms:

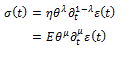
where 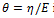is the time constant, while 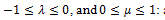an element with these characteristics is defined a spring-pot [11], since it possesses the properties of both a spring and a dashpot.

Taking the Laplace transform of equation (2), Craiem and co-workers [12] used the complex Young’s modulus 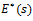in the frequency domain, given by

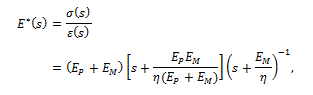
to get, from equation (2), the fractional differential equation ruling the spring-pot in the form

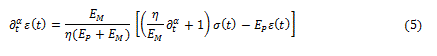
for which the stress-strain relationship is

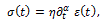
whereas the fractional version of the complex Young’s modulus is

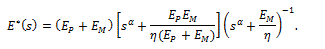
Using this mathematical framework, in which the spring-pot substituted the dashpot of a standard linear solid model, it was then possible to validate the experimental results using some segments of the human ascending aorta from donors died not for atherosclerosis-related causes [11], to obtain the values of 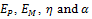at two different experimental levels of stress.

Many other possibilities of simulation are potentially useful in the study of the healthy as well as the pathological behavior of the human blood vessels: the elastic modulus exerts a significant effect on the blood transport along the various tissues and organs. Hence, one would expect that fractional calculus would be of paramount importance in the study, for example, of the blood vessels when, for any cause, the elastic components of the walls suddenly change along an artery: this is the case, for example, of the connection in the renal arteries after a renal transplant [13], or when stress is increased due to physiological or pathological factors [14-16].

References

1. Bergel DH (1961) The static elastic properties of the arterial wall. J Physiol 156: 445-457. [Crossref]
2. Bergel DH (1961) The dynamic elastic properties of the arterial wall. J Physiol 156: 458-69. [Crossref]
3. Love A (1944) A treatise on mathematical theory of elasticity, 4th ed. Dover Publications, New York.
4. Rubenstein DA, Yin W, Frame MW (2012) Biofluid mechanics. Academic Press, Oxford.
5. Wang Z, Golob M, Chesler NC (2016) Viscoelastic Properties of Cardiovascular Tissues, in El-Amin MF, Ed.: Viscoelastic and Viscoplastic Materials. InTech, Rijeka.
6. Woo SL (2004) Contribution of biomechanics to clinical practice in orthopaedics. Conf Proc IEEE Eng Med Biol Soc 7: 5455. [Crossref]
7. Fung YC (1997) Biomechanics: circulation, 2nd Ed. Springer Verlag, New York.
8. Oldham KB, Spanier J (1997) The fractional calculus. Academic Press, New York.
9. Podlubny I (1999) Fractional differential equations. Academic Press, San Diego.
10. Mainardi F (2010) Fractional calculus and waves in linear viscoelasticity. Imperial College Press, London.
11. Koeller RC (1984) Applications of fractional calculus to the theory of viscoelasticity. J Appl Mech 51: 299-307.
12. Craiem DO, Rojo FJ, Atienza JM, Guinea GV, Armentano RL (2008) Fractional calculus applied to model arterial viscoelasticity. Latin Amer Appl Res 38: 141-145.
13. Pallotti G, Donati G, Capelli I, Baraldi O, Comai G, et al. (2015) Donor/recipient delta age: a possible risk for arterial stenosis in renal transplantation. Comput Math Methods Med 2015:512929.
14. Xiao H, Tan I, Butlin M, Li D, et al. (2017) Arterial viscoelasticity: role in the dependency of pulse wave velocity on heart rate in conduit arteries. Am J Physiol Heart Circ Physiol 312: H1185-1185H1194. [Crossref]
15. Balzani D, Deparis S, Fausten S, Forti D, Heinlein A, et al. (2016) Numerical modeling of fluid-structure interaction in arteries with anisotropic polyconvex hyperelastic and anisotropic viscoelastic material models at finite strains. Int J Numer Method Biomed Eng 32.
16. Taniguchi R, Hosaka A, Miyahara T, Hoshina K, Okamoto H, et al. (2015) Viscoelastic Deterioration of the Carotid Artery Vascular Wall is a Possible Predictor of Coronary Artery Disease. J Atheroscler Thromb 22: 415-423. [Crossref]