A general schema is presented for how metabolic homeostasis is set and maintained. Energy (ATP) production by glycolysis* and oxidative phosphorylation is regulated through near equilibrium reactions. The near equilibrium reactions* provide a set point that is stable over time yet exquisitely sensitive to temporal changes in metabolic status. Energy (ATP) is produced “on demand” through direct coupling of ATP production to the rate of ATP consumption. The equilibrium constants for the near equilibrium reactions set the energy state ([ATP]/[ADP][Pi]) and this controls the activity of a downstream irreversible reaction. The thermodynamic component (equilibrium constant) assures long term stability while modulation of the concentration of individual metabolites of the mass action ratio provides rapid, sensitive, bidirectional interaction with surrounding cellular metabolism. The concentrations of metabolites in the mass action ratio for the internal near equilibrium reactions provides “fine tuning” of the relationship of the rate of ATP synthesis to the energy state. Once a set point for the energy state was established in the earliest lifeforms, the set point was retained. As evolution added metabolism to support increasingly complex organisms, the added metabolism was constrained to being consistent with, and supportive of, that set point.
*Throughout this paper we use the term “near equilibrium” to describe reactions where the net flux is usually less than one third of the forward rate and the direction is readily reversible. This corresponds to a free energy change (ΔG of ± 0.65 Kcal/mole or 2.7 KJ/mole). Our discussion of glycolysis is limited to its role in energy metabolism i.e., to the section from phosphofructokinase through pyruvate kinase.
ATP consumption, cellular metabolism, phosphofructokinase
Fundamental metabolic requirements for development of life
Evolution is a process that makes use of available chemistry to develop metabolic pathways that provide the energy and materials required to build and sustain living organisms. This is done through catalysts that enhance the rates of reactions “useful” to the organisms. In this case, “useful” reactions are those which increase the ability of the organism to survive and multiply in an environment where the available resources are limited and are being competed for by other organisms. Changes in the activity and/or specificity of the catalysts are not goal directed, but the limited availability of raw materials and competition with other organisms for these raw materials leads to “survival of the fittest”. The probability that a change in metabolism will be retained is determined by whether it improves the organism’s survival and/or reproduction capabilities. Species diversify through change in the genes that codify their catalytic complement, and thereby their metabolism and its regulation.
In order to survive and reproduce, living organisms continuously assemble complex structures at both molecular (RNA, DNA, proteins, etc.) and physical (membranes, organelles etc.) levels, as well as establish and maintain non-equilibrium distributions of small molecules and ions. Energy is required to overcome the negative entropy associated with making and maintaining order as well as to overcome the positive free energy associated with synthesis of the many required molecules. Maintaining a robust, stable source of energy for doing chemical and physical work is the first and most essential requirement for the existence of life. Examination of metabolism in organisms with widely different evolutionary histories shows their energy metabolism is remarkably similar. This is consistent with their having originated from a common ancestor and metabolism having an evolutionarily stable core. Metabolism has both thermodynamic and kinetic components, i.e., near equilibrium reactions (thermodynamic) and irreversible reactions far displaced from equilibrium (kinetics). Thermodynamic parameters are evolutionarily stable whereas the kinetic parameters are highly variable. The evolutionarily stable core of metabolism must, therefore, be based on thermodynamics. We need to understand how life, a non-equilibrium process, is based on, and regulated by, the near equilibrium reactions. Wilson and Matschinsky proposed that metabolism has a thermodynamic set point (homeostasis) determined by near equilibrium reactions that control energy production by glycolysis [1]. This concept is extended in the present paper with proposal of a general schema in which near equilibrium reactions coupled to ATP synthesis determine the flux through a downstream irreversible reaction. This design is shown to apply to ATP production by both glycolysis and oxidative phosphorylation, providing a thermodynamic base for energy metabolism that is stable over time yet exquisitely sensitive to temporal changes in metabolic status. Energy (ATP) is provided “on demand” through direct coupling of the rate of ATP production to the rate of ATP consumption. Flux is dependent on the mass action ratio of the near equilibrium reactions, and this functionally stabilizes the cellular energy state ([ATP]/[ADP][Pi]). Alterations in the rate of ATP consumption are immediately countered by changes in [ADP] and [Pi] and these act to reestablish equality between consumption and production. Once the set point was established in the earliest lifeforms, it has been retained in all subsequent life forms. As evolution added metabolism to support increasingly complex organisms, the added metabolism was constrained to being consistent with, and supportive of, that set point.
Design of metabolic pathways for energy production, and how that design leads to a homeostatic set point
Two major metabolic pathways for ATP production in eukaryotes are glycolysis (the Embden-Meyerhof-Parnas pathway) and oxidative phosphorylation. The energy (ATP) producing part of glycolysis and oxidative phosphorylation have similar design and regulation, although using very different chemistry. Both use a schema for ATP production that has two parts, shown as simple hypothetical chemical reactions (non-enzymatic) in equations 1 and 2 below. The first part of the pathway, equation (1), consumes metabolite(s), A, ADP, and Pi, producing ATP and B as products. This part of glycolysis is fully reversible and near equilibrium. The near equilibrium reaction is followed by an irreversible reaction that may also be coupled to ATP synthesis. The product(s) of the near equilibrium reaction is consumed by the irreversible reaction with further production of a product (C):
A + nADP + nPi = nATP + B (1)
B ---> C (2)
Reaction 2 may, or may not, also be coupled to ATP synthesis.
Simulation of control of the generic chemical pathway illustrated by reactions 1 and 2
For chemical reactions in a test tube, the equilibrium constant (Ke) for reaction (1) is:
Ke = [B]/[A] x ([ATP]/[ADP][Pi])n (3)
The rate of ATP synthesis (Vatp) would then be the flux through the irreversible reaction (2):
Vatp = k x [B] (4)
Where k is the first order rate constant for reaction 2. Solving for [B] in equation (3) and substituting into equation (4), the rate of ATP synthesis becomes:
Vatp = Ke x k x [A] x ([ADP][Pi]/[ATP])n (5)
When there is a continuous state source of A, but a limiting total adenine nucleotide concentration, the reaction is controlled by the rate of ATP consumption. ATP consumption is the source of essential metabolites ADP and Pi. For any given rate of ATP consumption, the value of the energy state ([ATP]/[ADP][Pi] is determined largely by the equilibrium constant (Ke) and tightly regulated. When the concentration of A is constant (steady state) the rate of ATP synthesis is equal to a constant (Ke x k x [A]) multiplied by ([ADP][Pi]/[ATP])n. In metabolism, there are ATP producing reactions with effective n values of 1, 2, and 3. The behavior of a hypothetical chemical system has been simulated for all three values for n (Figures 1A and 1B). The higher the value of n, the greater the increase in rate of ATP synthesis associated with a given decrease in energy state. In Figure 1 the decrease in energy state is presented as the associated increase in [ADP] (Figure 1A) or [AMP] (Figure 1B). Thus, the change in rate of synthesis in associated with a change in [ADP] (sensitivity) increases with increase in n value.
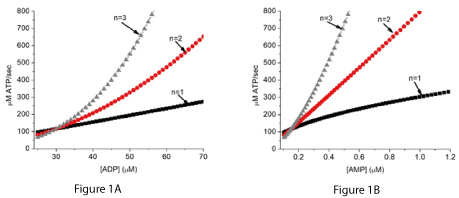
Figure 1A and 1B. The rate of ATP synthesis in the hypothetical chemical system (equations 1 and 2) in relation to [ADP] and [AMP].
The simulations assumed equilibrium constants for reaction 1 with n values of 1, 2, and 3 that gave the same rate of ATP synthesis near an [ADP] of 30 µM.
Figure 2A shows the relationship of the rate of ATP synthesis to [ADP] for different values for the equilibrium constant (Ke) for reaction 1. The simulations assumed [A] of 80 µM, total adenine nucleotide ([ATP]+[ADP]+[AMP]) of 6 mM, and [Pi] of 4 mM. No contribution of the creatine phosphokinase reaction is included. Figure 2B shows the effect of varying [A] on the rate of ATP synthesis when the equilibrium constant Ke is 6.7 x 103 M-2 and rate constant k is 7.2 x 105/sec. These values were chosen to generate energy states consistent with tissue in vivo. A dashed horizontal line has been placed for a synthesis rate of 240 µM ATP/sec.
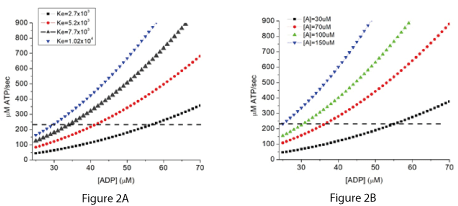
Figures 2A and 2B. Simulated effect of changing the equilibrium constant (Ke) or substrate (A) concentration on the rate of ATP synthesis when the n value is 2.
When the total concentration of adenine nucleotides ([ATP]+[ADP]+[AMP]) is small relative to the flux through the system, the rate of ATP synthesis is demand (consumption) limited. ATP has to be consumed to provide the essential reactants ADP and Pi, and the rate of ATP synthesis is stoichiometrically coupled to the rate of ATP consumption. The effect of varying the equilibrium constant (Ke) and reactant (A) concentration on the rate of ATP synthesis are presented in Figure 2A and B for an n value of 2. A horizontal line has been placed on the figures for a rate of ATP synthesis of 240 µM/sec. Where this line intersects the curves shows the [ADP] at which this rate of ATP consumption would be equaled by the rate of production (steady state). When ATP consumption exceeds production, [ADP] and [Pi] increase. This increases production until it again equals consumption. Conversely if ATP consumption falls below production, ADP and Pi decrease, lowering production until it again matches consumption.
The energy (ATP) producing reactions of glycolysis: transformation of glyceraldehyde-3-phosphate to pyruvate
In contrast to the general chemical reaction described above, in glycolysis, the reactions are enzyme catalyzed. This does not affect treatment of the near equilibrium reactions, but I glycolysis there is increased complexity due to the additional reactants in the equilibrium (NAD+ and NADH). The near equilibrium part of glycolysis consists of the sequence of reactions by which glyceraldehyde-3-phosphate to (G-3-P) is oxidized to phosphoenolpyruvate (PEP), producing ATP, NADH, and PEP. The component reactions are combined as shown in equation (6):
G-3-P + Pi + NAD+ + ADP = NADH + ATP + PEP (6)
Because all three reactions contributing to reaction (6) are near equilibrium, they behave as a single reaction and have an overall equilibrium constant. PEP produced by the near equilibrium reaction is then converted to pyruvate in an irreversible reaction catalyzed by pyruvate kinase (PK). The PK reaction synthesizes an additional ATP from ADP and phosphate from PEP:
PEP + ADP ---> Pyr + ATP (7) The equilibrium constant for reaction (6) (K2) includes NAD+ and NADH.
K2 = [PEP]/[G-3-P] x [NADH]/[NAD+] x [ATP]/[ADP]f[Pi]f (8)
Where [PEP] and [G-3-P] are the concentrations of phosphoenolpyruvate and glyceraldehyde-3-phosphate, respectively. A subscript, f, has been added to [ADP] and [Pi] to indicate it is the free, not total, concentration of ADP that is relevant. The activity of PK is simulated as a random bi-bi enzyme reaction mechanism [1]:
1/v = 1/Vm + KMadp / (Vm x [ADP]) + KMpep/(Vm x [PEP])+ KMpep x KMadp/(Vm x [ADP]f[PEP]) (9)
where KMadp and KMpep are the Michaelis constants for ADP and PEP, respectively, and Vm is the maximal activity of PK as measured at saturation with both substrates. Equation (8) was used to solve for [PEP] at any value for [ADP]f and [NADH]/[NAD+]. Flux through PK was then calculated from equation (9). In our earlier paper, it was assumed that there was no product inhibition because pyruvate is not inhibitory [1,2]. ATP binds in the active site in the muscle form of PK and competes with both ADP and PEP [2], but for physiological conditions [ATP] is nearly constant and the [ATP] dependence was not included in our simulations. Inclusion of this [ATP] dependence slightly changes the behavior. The rate becomes dependent on ([ATP]/[ADP][Pi])2 instead of ([ATP]/ADP]2[Pi]2). Thus, the rate depends on energy state and does not have a dependence on [ADP] or [Pi] per se.
Figure 3A shows the effect of 5 different values of K2 on the relationship of [ADP] to the net rate of synthesis of ATP when the rate of ATP consumption is 138 µM ATP/sec (8 µM Pyr/sec), maximal PK activity is 645 µM/sec and [A] is 8 µM. The concentration of total adenine nucleotides (ATP+ADP+AMP) was 6 mM, [Pi] was 8 mM, and total creatine (creatine + creatine phosphate) was 40 mM. K2 calculated from measurement of metabolites is approximately 800 M-1, and the curves for this value of K2 are indicated by the larger triangles. Figure 3B shows the relationship of free [AMP]f to the rate of ATP synthesis. Adenylate kinase was assumed to be near equilibrium and a dashed vertical line is added at 1.8 µM free AMP. This is the concentration reported by Frederich and Balschi to result in half maximal activity of AMP dependent protein kinase (AMPK) in perfused rat heart [3].
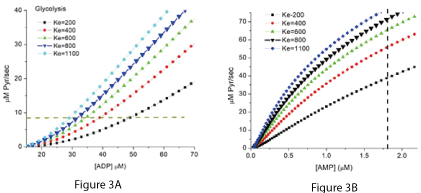
Figures 3A and 3B. The net rate of ATP synthesis by PK dependence on the equilibrium constant (K2) of the near equilibrium reactions.
In Figure 3A the rate of ATP synthesis is plotted against the associated [ADP]f. As the equilibrium constant increases there is a marked shift in the rate to lower [ADP] f. When K2 is equal to that calculated from the free metabolite concentrations in tissues (800M-1, indicated in the figure by larger symbols), the rate and [ADP] f are consistent with experimental measurements [4-8]. In figure 3B, the rate is plotted against the associated concentration of free AMP ([AMP]f). AMP has a major role in cellular metabolism, acting as a small molecule messenger that helps to integrate the rest of cellular metabolism with energy metabolism. Controlling the activity of AMP dependent protein kinase is one of the most important of those regulatory activities [9-15]. A dashed vertical line has been included in Figure 3B at the [AMP]f reported by Frederich and Balschi [3] to result in half maximal activity of AMPK under physiological conditions. Lowry and coworkers [16] reported a similar AMP concentration is a powerful activator of muscle phosphorylase.
Energy (ATP) production by oxidative phosphorylation
Mitochondrial oxidative phosphorylation couples the energy available when NADH is oxidized by molecular oxygen providing the energy for synthesis of ATP. This occurs with an overall stoichiometry of 3 ATP synthesized per NADH oxidized. The redox reactions occur in three steps, each step providing sufficient energy for ATP synthesis. The three steps are coupled through a common intermediate to the synthesis of ATP. Consistent with the generic pathway described earlier, oxidative phosphorylation consists of a near equilibrium reaction coupled to ATP synthesis followed by an irreversible reaction that is also coupled to ATP synthesis. The initial near equilibrium reaction incorporates the first two energy coupling sites:
NADH + 2 cyt c+3 +2 ADP + 2 Pi = NAD+ + 2 ATP + 2 cyt c+2 (10)
Transfer of two reducing equivalents from intramitochondrial NADH to oxidized cytochrome c (cyt c3+) is coupled to the synthesis of 2 ATP. The dependence of the reactions on pH is not included in order to simplify the presentation. Reaction (10) has been shown to be reversible in suspensions of isolated mitochondria [17-19] and in vivo measurements are consistent with the reactions being near equilibrium [19-22]. Reduced cytochrome c (cyt c2+) is then re-oxidized using molecular oxygen and producing water, by cytochrome c oxidase, in an irreversible reaction that is also coupled to synthesis of ATP:
2 cyt c2+ + ½ O2 + ADP + Pi + 2H+ ---> 2 cyt c3+ + ATP + H2O (11)
The mechanism of oxygen reduction by cytochrome c oxidase and overall kinetic behavior of reaction (11) has been modeled [23,24]. Addition of the near equilibrium reaction (10) to the kinetic expression for cytochrome c oxidase [25] provides a computational model that can accurately simulate the behavior of oxidative phosphorylation in a variety of tissues and over a wide range of in vivo conditions [26-29]. This includes energy metabolism in skeletal muscle during the large changes in rate of ATP consumption that occur during rest-to-work [21] and work-to-rest [27] transitions. The simulations of skeletal muscle metabolism include the creatine phosphokinase reaction and a total creatine concentration (creatine, [Cr], plus creatine phosphate, [CrP]), of 40 mM. As a result, [Pi] becomes an important contributor to the energy state. In Figure 4A, the rate of oxidative phosphorylation in rat skeletal muscle, expressed as the turnover number for mitochondrial cytochrome c, is plotted against the associated [ADP]f. The rate is low when [ADP]f is less than about 30 µM but increases rapidly with increase in [ADP] above 30 µM. In Figure 4B, the rate is shown in units that are more easily compared to experimental data. The rate of ATP synthesis in µM/sec is plotted against the associated creatine phosphate to creatine ratio ([CrP]/[Cr]). The rate is low, about 50 µM ATP/sec in resting muscle when [CrP]/[Cr] is high (above about 1.4). ATP synthesis increases rapidly with decrease in [CrP]/[Cr]. The dynamic range of energy metabolism in skeletal muscle in vivo is large. To facilitate comparison of these rates to experimental measurements, the cytochrome c TN and µM ATP/sec are about 2/sec, and 50 µM /sec, respectively, in resting muscle. These increase to near 20/sec and 1000 µM /sec in moderate work rates and can go above 100/sec and 5,000 µM ATP/sec at maximal work rates. Expressed as units more often used in physiology papers, the rates are 0.78, 15.6, and 78 ml O2/100 g tissue/min.
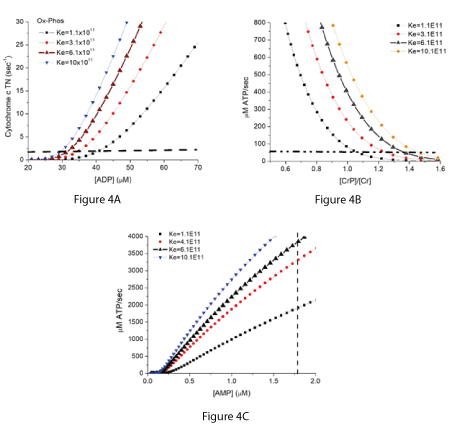
Figure 4A-4C. Simulation of the rate of oxidative phosphorylation in skeletal muscle and its associated values of [ADP] (4A), [CrP]/[Cr] (4B), and [AMP] (4C).
The simulations are for skeletal muscle in untrained rats assuming total creatine concentration of 40 mM and a cytochrome c concentration of 19 µM, with [ATP] and [Pi] under resting conditions of 6 mM and 2 mM, respectively [30-32]. The curves with larger solid black triangles are for the measured equilibrium constant of near 6 x 1011 M-2. Horizontal dashed lines show approximate values for cytochrome c turnover (1.5/sec) and ATP production/consumption (50 µM/sec) in resting skeletal muscle. The resting metabolic rates in skeletal muscle are low and dependent on experimental conditions. These values have been inferred from resting whole body heat production [33-35] and similar values have been reported for measurements in individual muscles [31,36]. The dashed vertical line in 4C marks an [AMP]f of 1.8 µM, the concentration reported to give 50% maximal activity of AMPK in rat heart muscle [3].
Metabolic constraints imposed on energy metabolism in eukaryotes: How glycolysis and oxidative phosphorylation are constrained to work together
Formation of mitochondria in eukaryotes is generally believed to have involved endocytosis of an ancestor of p. denitrificans by a prokaryote using glycolysis for energy production. Although both organisms were adapted to the same energy state, integration and coordination of the two ATP producing pathways was not simple. Oxidative phosphorylation requires the [NADH]/[NAD+] ratio be near 2 in order to maintain the energy state whereas for glycolysis the ratio needs to be near 0.002, making it impossible for the metabolic pathways to function within a single compartment [1,37]. It is essential that metabolism supplying NADH for oxidative phosphorylation remain in a separate compartment from glycolysis, i.e., separated by the mitochondrial inner membrane which is impermeable to NADH and NAD+. In addition, although the two pathways have a common set point for the energy state, change in rate of ATP production associated with a change in energy state (sensitivity) is different. The change in rate, other variables remaining constant, rate depends on ([ATP]/[ADP][Pi])2 (glycolysis) and approximately ([ATP]/[ADP][Pi])3 (oxidative phosphorylation). As a result, oxidative phosphorylation provides tighter control of metabolic homeostasis, i.e., less deviation from the set point for the same change in the rate of ATP consumption. Other evolutionarily advantageous characteristics include greater production of ATP from glucose (approx. 38 vs 2), ability to use a wide range of oxidizable substrates (carbohydrates, fatty acids, amino acids), less toxic and more readily eliminated products (CO2 and water vs lactic acid). These characteristics resulted in oxidative phosphorylation becoming the dominant ATP source for eukaryotes. Regulatory pathways evolved that coupled glycolysis to oxidative phosphorylation (pyruvate, glycerol phosphate shuttle, glutamate aspartate shuttle, etc) and controls (feedback regulation) that limited glycolytic ATP production to when oxidative phosphorylation is compromised due to lack of substrate (oxygen, NADH) or excessive demand.
Note: there are specialized metabolite sensor (glucose, oxygen) cells in which alternative sources of ATP are limited and feedback regulation is largely absent. The concentration of the sensed metabolite, other parameters held constant, then becomes coupled to the energy state. For glucose sensing (pancreatic beta cells and neurons) the cells rely on glycolysis as their primary energy source and have glucokinase (low affinity for glucose, not feedback inhibited) for the first step in glycolysis. This results in the energy state being a function of glucose concentration [28,38]. Parallel design of metabolism of oxygen sensing cells (carotid body, arterial bodies, neurons) with oxidative phosphorylation as the primary ATP source and intramitochondrial [NADH]/[NAD+] held constant, results in mitochondrial cytochrome c oxidase acting as a sensitive oxygen sensor [28,39-41]. In non-sensory cells, it is important that energy metabolism not be critically dependent on a single substrate. They have hexokinase (high affinity for glucose, feedback inhibited) instead of glucokinase, glycolysis as well as oxidative phosphorylation for ATP production, and NADH production through the citric acid cycle, fatty acid oxidation etc is highly regulated. In non-sensory cells, oxidative phosphorylation is dependent on several metabolic parameters and changes in any one or more of these parameters can result in altered energy state. To obtain cells specific for sensing each variable, additional layers of control have been added; notably sensors for fatty acids, amino acids, and oxygen (hypoxia inducible factors [42,43].
What about procaryotic organisms that use nitrate or sulfate as terminal electron acceptors?
There are a large number of organisms that do not use glycolysis or oxygen dependent oxidative phosphorylation as their energy source. The nitrate reducing procaryotes include p. denitrificans, for which the metabolism has been extensively studied. It has been proposed that an ancestor of p. denitrificans was endocytosed and evolved into mitochondria [44-47]. P. denitrificans can grow anaerobically with nitrate as the electron acceptor or aerobically with oxygen as the electron acceptor. During anaerobic nitrate reduction, electrons from the potential of the cytochrome c/pseudoazurin region of the respiratory chain are donated to nitrate reductase. Nitrate reductase, like cytochrome c oxidase, catalyzes an irreversible reaction. Unlike cytochrome c oxidase, however, nitrate reductase is not coupled to ATP synthesis. This results in a pathway with the rate dependent on the square of the energy state, due to near near equilibrium from NADH to cytochrome c. P. denitrificans has energy metabolism and energy state set point similar to mitochondria in eukaryotes [23,44-47]. The great diversity of other organisms, including those using nitrogen or sulfur metabolism as their energy sources, precluded definitive generalizations on how they maintain their energy state. Where measurements have been made, however, the similarities in their genetic material, enzymes, and nucleic acids are consistent with a common set point for energy metabolism [48-55].
Enzyme activities particularly important to the regulation of metabolism by the energy state:
Nucleoside diphosphate kinase (EC 2.7.4.6)
NDK is responsible for maintaining near equilibrium of phosphate transfer among the nucleoside di and tri phosphates, assuring they have similar triphosphate to diphosphate ratios [56,57]. This activity is universally present in cells. Although most of the activity is in the cytoplasm, it is also present in the mitochondria. Among other things, NDK coordinates the nucleic acids required for synthesis of RNA and DNA, assuring they have a common response to changes in energy state and factors affecting the energy state.
Nucleoside monophosphate kinase (EC 2.7. 4.3)
This enzyme activity catalyzes phosphorylation of nucleoside monophosphate to form nucleoside diphosphate [58]. The classical NMK is adenylate kinase (myokinase). The activity of these enzymes is not very specific for the nucleic acid part of the substrate, and the equilibrium constants for NMK reactions are nearly the same. All of the nucleoside monophosphates are maintained near equilibrium with their nucleoside di and tri-phosphates. The energy state directly determines the ratios among the concentrations of the free mono-, di, and tri-phosphate forms. The total amount of individual nucleosides, i.e., sum of the concentrations of the mono, di, and tri-phosphate forms, is independently regulated through de novo synthesis and salvage pathways. NMK determines the concentration ratios and not the absolute concentrations.
AMP dependent protein kinase
Phosphate transfer among ATP, ADP, and AMP is equilibrated by adenylate kinase, assuring that free [AMP] is a sensitive indicator of the energy state. An important regulatory function of [AMP]f is control of the activity of AMPK, a protein kinase with a major role in regulating energy metabolism and cellular biology in general. AMPK and its roles in regulating metabolism have been extensively discussed [9-15,59] and therefore are not discussed in detail here.
A general schema for how metabolic homeostasis is set and maintained is represented in Figure 5. ATP is synthesized by energy producing pathways represented by glycolysis and oxidative phosphorylation. These pathways set the energy state through internal near equilibrium reactions, the activity of a downstream irreversible reaction, and the mean rate of ATP consumption. The rate of ATP synthesis is determined by demand (rate of ATP consumption), with flux control by the energy state. The thermodynamic component (equilibrium constant) assures long term stability while the modulation of the concentration of individual metabolites of the mass action ratio provides rapid, sensitive, bidirectional interaction with the surrounding cellular metabolism. The energy producing pathways, in conjunction with mean cellular rate of ATP consumption (demand), set the value of the energy state ([ATP]/[ADP][Pi]). Modulation of the levels of metabolites in the mass action ratio for the internal near equilibrium reactions provides “fine tuning” of the relationship of the rate of ATP synthesis to the energy state. The energy state associated with any particular rate of ATP synthesis (equals consumption) can be modulated by altering substrate concentrations i.e., increase in intramitochondrial [NADH]/[NAD+] or cytosolic [G-3-P] increases the energy state for any given rate of ATP production. Although increase in the rate of ATP synthesis is most often associated with a decrease in energy state, as exemplified by increased work rate in muscle, this is not essential. Consumption of ATP, which determines the rate of ATP synthesis, is largely independent of the metabolism that sets intramitochondrial [NADH]/[NAD+] and [G-3-P]. As a result, during normal metabolic transitions increase in the rate of ATP consumption may be associated with no change, increase, or decrease in the energy state. The concentrations/concentration ratios of many essential metabolites are coupled to the energy state by near equilibrium enzymes, such as NDK and NMK, as well as activation/inhibition enzymes like AMPK. Through these metabolites the energy state communicates with and has a central role in regulation of virtually all cellular metabolism and function. The whole provides the stability referred to as metabolic homeostasis.
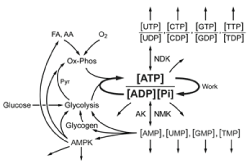
Figure 5. A schematic representation of the core reactions that determine metabolic homeostasis.
Metabolic homeostasis is determined by the cellular energy state, and this is set and maintained through near equilibrium reactions that regulate the ATP producing pathways, represented by glycolysis and oxidative phosphorylation. The energy state communicates with all of cellular metabolism through the concentrations of ATP, ADP, AMP, and Pi. Near equilibrium reactions catalyzed by nucleoside diphosphate and nucleoside monophosphate kinases (NDK, NMK and AK) result in the energy state setting the comparable parameters for all of the other nucleotide phosphates. In combination, the nucleoside concentrations and concentration ratios are critical regulators of most of the cellular metabolism, particularly that related to RNA and DNA. Of notable importance is the role of [AMP]f, which regulates AMPK (AMP dependent protein kinase) a protein kinase which has a major role in regulating cellular metabolism. The open-ended arrows represent the large number of additional regulatory functions carried out by the indicated metabolites and metabolite ratios. Essentially all of metabolism is directly or indirectly coupled to, and dependent on, the energy state.
On metabolic homeostasis and its “set point”
Cellular metabolism can be said to be in homeostasis when the cells are fully functional, i.e., they are viable, able to proliferate and/or carry out their specialized functions within the tissues of differentiated organisms. To maintain full functionality, the energy state needs to fall within a range of values that can be described as a Gaussian distribution with a peak equal to the homeostatic “set point” (Figure 6). The cellular energy state may take on values (non-viable) outside of the Gaussian distribution for many reasons. When the energy state falls outside of that viable distribution Gaussian, the cells are stressed and no longer able to maintain full functionality. Conditions with acutely altered energy states have been extensively studied. These have generally focused on conditions that decrease the energy state, such as acute hypoxia, hypoglycemia, and increased muscle work, but there are also conditions with increased energy state, such ingestion of fructose, ethanol or glycerol, and treatment with hyperbaric oxygen. As long as the displacements are within the regulated range for that cell type, and not sustained for too long, the cells recover. Muscle cells, for example, can tolerate large increases in work load as long as the decrease in energy state remains within the regulated range, the duration is sufficiently short, and work is followed by suitable rest. If any of these criteria are not met, pathology results.
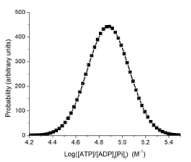
Figure 6. A hypothetical Gaussian distribution of energy state for viable cells.
The energy state is calculated as ([ATP]/[ADP]f[Pi]f) where [ADP]f and [Pi]f are the free (unbound) concentrations. The Gaussian distribution is a reasonable assumption, but not verified. We estimate the peak is at approx. 75,000M-1 and at half height the range is from 4.7 to 5.1 (50,000 to 126,000 M-1). These estimates based on measurements for skeletal muscle, liver, heart, and brain, but should be viewed with caution (Figure 6).
Less well understood are the physiological effects of chronic displacements of the energy state, because these displacements are small and pathology, when observed, develops slowly, over months to years. In animals, chronically low energy states are associated with compromised metabolite delivery (hypoxia, hypoglycemia, starvation) and chronically high energy states with metabolite oversupply (type 2 diabetes, obesity). Long term displacement in energy can result in changes in gene expression and metabolism that counter the displacement in energy state. Decrease in energy state can be countered by suppressing ATP consumption, such as cells becoming quiescence, or increasing reduction of intramitochondrial [NADH]/[NAD+] and/or increase in [G-3-P], which acts to counter the decrease in energy state. Increase in energy state due to oversupply of foodstuffs, particularly sugars, can be countered by increased synthesis and storage of fats, but chronic oversupply can lead to obesity and type 2 diabetes. Whatever the cause, chronic displacement of energy state from viability (into the grey zone) results in progressive increase in phenotypic changes, probability of cell death and genetic mutations. The latter can give rise to irreversibly altered surviving cell lines.
Neither DFW nor FMM have any financial and personal relationships that could influence (bias) the work presented in this manuscript.
- Wilson DF, Matschinsky FM (2021) Metabolic homeostasis in life as we know it: Its origin and thermodynamic basis. Front Physiol 12: 658997. [Crossref]
- Reynard AM, Hass, LF, Jacobsen DD, Boyer PD (1961) The correlation of reaction kinetics and substrate binding with the mechanism of pyruvate kinase. J Biol Chem 236: 2277-2283. [Crossref]
- Frederich M, Balschi JA (2002) The relationship between AMP-activated protein kinase activity and AMP concentration in the isolated perfused rat heart. J Biol Chem 27: 1928-1932. [Crossref]
- Veech RL, Lawson JWR, Cornell NW, Krebs HA (1979) Cytosolic phosphorylation potential. J Biol Chem 254: 6538-6547. [Crossref]
- Davies KJA, Packer L, Brooks GA (1981) Biochemical adaptation of mitochondria, muscle, and whole-animal respiration to endurance training. Arch Biochem Biophys 299: 539-554. [Crossref]
- Dudley GA, Tullson PC, Terjung RL (1987) Influence of mitochondrial content on the sensitivity of respiratory control. J Biol Chem 262: 9104–9114. [Crossref]
- Tullson PC, Rush JWE, Wieringa B, Terjung RL (1998) Alterations in AMP deaminase activity and kinetics in skeletal muscle of creatine kinase-deficient mice. Am J Physiol 274 (Cell Physiol. 43): C1411–C1416. [Crossref]
- Haseler LJ, Hogan MC, Richardson RS (1999) Skeletal muscle phosphocreatine recovery in exercise-trained humans is dependent on O2 availability. J Appl Physiol 86(6): 2013-2018. [Crossref]
- Hardie DG, Ross FA, Hawley SA (2012) AMPK - a nutrient and energy sensor that maintains energy homeostasis. Nat Rev Mol Cell Biol 13: 251-262. [Crossref]
- Evans AM, Hardie DG (2020) AMPK and the need to breathe and feed: What’s the matter with oxygen? Int J Mol Sci 21: 3518. [Crossref]
- Evans AM, Mahmoud AD, Moral-Sanz J, Hartmann S (2016) The emerging role of AMPK in the regulation of breathing and oxygen supply. Biochem J 473: 2561-2572. [Crossref]
- Garcia D, Shaw RJ (2017) AMPK: Mechanisms of cellular energy sensing and restoration of metabolic balance. Molecular Cell 66: 789-799. [Crossref]
- González A, Hall MN, Lin SC, Hardie DG (2020) AMPK and TOR: The Yin and Yang of cellular nutrient sensing and growth control. Cell Metabolism 31: 472-492. [Crossref]
- Herzig S, Shaw RJ (2018) AMPK: guardian of metabolism and mitochondrial homeostasis. Nature Rev Mol Cell Biol 19: 121-135. [Crossref]
- Mihaylova MM, Shaw RJ (2012) The AMP-activated protein kinase (AMPK) signaling pathway coordinates cell growth, autophagy, & metabolism. Nat Cell Biol 13: 1016–1023. [Crossref]
- Lowry OH, Schultz DW, Passonneau JV (1964) Effects of adenylic acid on the kinetics of muscle phosphorylase a. J Biol Chem 239: 1947-1953. [Crossref]
- Klingenberg M, Schollmeyer P (1961) On the reversibility of oxidative phosphorylation III. Effect of adenosine triphosphate on the respiratory chain in respiratory inhibited mitochondria. Biochem Z 335: 243-262. [Crossref]
- Chance B, Hollunger G (1961) The Interaction of energy and electron transfer reactions in mitochondria VI. The efficiency of the reaction. J Biol Chem 236: 1577-1584. [Crossref]
- Erecinska M, Veech RL, Wilson DF (1974) Thermodynamic relationships between the oxidative-reduction reactions and ATP synthesis in suspensions of isolated pigeon heart mitochondria. Arch Biochem Biophys 160: 412-421. [Crossref]
- Wilson DF, Stubbs M, Veech RL, Erecinska M, Krebs HA (1974C) Equilibrium relations between the oxidation-reduction reactions and ATP synthesis in suspensions of isolated liver cells. Biochem J 140: 57-64. [Crossref]
- Wilson DF (2015) Regulation of metabolism: the rest-to-work transition in skeletal muscle. Amer J Physiol – Endocrinol Metab 309: E793-E801. [Crossref]
- Wilson DF (2017) Oxidative phosphorylation: regulation and role in cellular and tissue metabolism. J Physiol 595: 7023-7038. [Crossref]
- Wilson DF, Owen CS, Erecinska M (1979A) Quantitative dependence of mitochondrial oxidative phosphorylation on oxygen concentration. Arch Biochem Biophys 195: 494-504. [Crossref]
- Wilson DF, Stubbs M, Oshino N, Erecinska M (1974B) Thermodynamic relationships between the mitochondrial oxidation-reduction reactions and cellular ATP levels in tumor cells and perfused rat liver. Biochemistry 13: 5305-5311. [Crossref]
- Wilson DF, Vinogradov SA (2014) Mitochondrial cytochrome c oxidase: mechanism of action and role in regulating oxidative phosphorylation. J Appl Physiol 117: 1431-1439, 2014. [Crossref]
- Wilson DF (2013) Regulation of cellular metabolism: Programming and maintaining metabolic homeostasis. J Appl Phys 115: 1583-1588. [Crossref]
- Wilson DF (2016) Regulation of metabolism: the work-to-rest transition in skeletal muscle. Am J Physiol Endocrinol Metab. 310: E633-E642. [Crossref]
- Wilson DF, Matschinsky FM (2019) Oxygen dependence of glucose sensing: role in glucose homeostasis and related pathology. J Appl Physiol 126: 1746-1755. [Crossref]
- Wilson DF (2016) Oxidative phosphorylation: unique regulatory mechanism and role in metabolic homeostasis. J Appl Physiol 122: 611-619. [Crossref]
- Schollmeyer P, Klingenberg M (1962) Über den Cytochrom-Gehalt tierischer Gewebe. Biochem Z 335: 426-439. [Crossref]
- Behnke BJ, Barstow TJ, Kindig CA, McDonough P, Musch TI, et al. (1981) Biochemical adaptation of mitochondria, muscle, and whole-animal respiration to endurance training. Arch Biochem Biophys 299: 539-554. [Crossref]
- Iles RA, Stevens AN, Griffiths JR, Morris PG (1985) Phosphorylation status of liver by 31P-n.m.r. spectroscopy, and its implications for metabolic control: A comparison of 31P-n.m.r. spectroscopy (in vivo and in vitro) with chemical and enzymic determinations of ATP, ADP and Pi. Biochem J 229: 141-151. [Crossref]
- Elia M (1992) Organ and tissue contribution to metabolic rate. In: Kinney JM, Tucker HN, eds. Energy metabolism: tissue determinants and cellular corollaries. New York, NY: Raven Press, 1992:61–80.
- Heymsfield SB, Peterson CM, Bourgeois B, Thomas DM, Gallagher D, et al. (2018) Human energy expenditure: Advances in organ-tissue prediction models. Obes Rev 19: 1177-1188. [Crossref]
- Wang Z-M, Ying Z, Bosy-Westphal A, Zhang J, Schautz S, et al. (2010) Specific metabolic rates of major organs and tissues across adulthood: evaluation by mechanistic model of resting energy expenditure. Am J Clin Nutr 92: 1369-1377. [Crossref]
- Behnke BJ, Barstow TJ, Kindig CA, McDonough P, Musch TI, et al. (2002) Dynamics of oxygen uptake following exercise onset in rat skeletal muscle. Resp Physiol Neurobiol 133: 229-239. [Crossref]
- Williamson DH, Lund P, Krebs HA (1967) The redox state of free nicotinamide-adenine dinucleotide in the cytoplasm and mitochondria of rat liver. Biochem J 103: 514-526. [Crossref]
- Matschinsky FM, Wilson DF (2019) The central role of glucokinase in glucose homeostasis: A perspective 50 years after demonstrating the presence of the enzyme in islets of Langerhans. Front Physiol 10: 148. [Crossref]
- Iturriaga R, Rumsey WL, Mokashi A, Spergel D, Wilson DF, et al. (1991) In vitro perfused-superfused cat carotid body for physiological and pharmacological studies. J Appl Physiol 70, 1393-1400. [Crossref]
- Wilson DF, Mokashi A, Chugh D, Vinogradov SA, Osanai S, et al. (1994) The primary oxygen sensor of the cat carotid body is cytochrome a3 of the mitochondrial respiratory chain. FEBS Lett 351: 370-374. [Crossref]
- Wilson DF, Matchinsky FM (2018) Metabolic homeostasis: Oxidative phosphorylation and the metabolic requirements of higher plants and animals. J Appl Physiol 125: 1183-1192. [Crossref]
- Semenza GL (2019) Pharmacologic targeting of hypoxia-inducible factors. Annu Rev Pharmacol Toxicol 59: 379–403. [Crossref]
- Gunton JE (2020) Hypoxia-inducible factors and diabetes. J Clin Invest 130: 5063-5073. [Crossref]
- Margulis L (1970) Origin of eukaryotic cells. Yale University Press, New Haven, CT.
- John P, Whatley FR (1975) Paracoccus denitrificans and the evolutionary origin of the mitochondrion. Nature 254: 495–498. [Crossref]
- John P, Whatley FR (1977) The bioenergetics of paracoccus denitrificans. Biochim Biophys Acta 463: 129-153. [Crossref]
- Gray MW (2012) Mitochondrial Evolution. Cold Spring Harb Perspect Biol, Eds: Douglas C. Wallace and Richard J. Youle 4: a011403. [Crossref]
- Berks BC, Ferguson SJ, Moir JWB, Richardson DJ (1995) Enzymes and associated electron transport systems that catalyse the respiratory reduction of nitrogen oxides and oxyanions. Biochim Biophys Acta 1232: 97-173. [Crossref]
- Bräsen C, Esser D, Rauch B, Siebers B (2014) Carbohydrate metabolism in Archaea: Current insights into unusual enzymes and pathways and their regulation. Microbiol Mol Biol Reviews 78: 89-175. [Crossref]
- Detmers J, Brüchert V, Habicht KS, Kuever J (2001) Diversity of sulfur isotope fractionations by sulfate-reducing prokaryotes. Appl Environ Microbiol 67: 888-894. [Crossref]
- Ronimus RS, Morgan HW (2003) Distribution and phylogenies of enzymes of the Embden-Meyerhof-Parnas pathway from archaea and hyperthermophilic bacteria support a gluconeogenic origin of metabolism. Archaea 1: 199-221. [Crossref]
- Sauer U, Eikmanns BJ (2005) The PEP-pyruvate-oxaloacetate node as the switch point for carbon flux distribution in bacteria. FEMS Microbiol Rev 29: 765-794. [Crossref]
- Edirisinghe JN, Weisenhorn P, Conrad N, Xia F, Overbeek R, et al. (2016) Modeling central metabolism and energy biosynthesis across microbial life. BMC Genomics 17: 568.
- Wenk CB, Wing BA, Halevy I (2018) Electron carriers in microbial sulfate reduction inferred from experimental and environmental sulfur isotope fractionations. The ISME J 12: 495–507. [Crossref]
- Zhang Y, Kouril T, Snoep JL, Siebers B, Barberis M, et al. (2017) The peculiar glycolytic pathway in hyperthermophylic archaea: Understanding its whims by experimentation in silico. Int J Mol Sci 18: 876. [Crossref]
- Schaertl S, Konrad M, Geeves MA (1998) Substrate specificity of human nucleoside-diphosphate kinase revealed by transient kinetic analysis. J Biol Chem 273: 5662-5669. [Crossref]
- Wilson DF, Erecinska M, Schramm V (1983) Evaluation of the relationship between the intra- and extramitochondrial [ATP]/[ADP] ratios using phosphoenolpyruvate carboxykinase. J Biol Chem 258: 10464-10473. [Crossref]
- Van Rompay AR, Johansson M, Karlsson A (2000) Phosphorylation of nucleosides and nucleoside analogs by mammalian nucleoside monophosphate kinases. Pharmacology Therapeutics 87: 189–198. [Crossref]
- Hardie DG (2015) AMPK: positive and negative regulation, and its role in whole-body energy homeostasis. Current Opinion in Cell Biology 33: 1-7. [Crossref]






