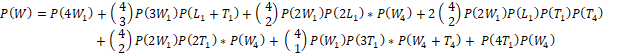Background: Early recognition of mild cognitive impairment (MCI) and subtle changes to cognitive abilities that precede an MCI diagnosis has the potential to improve the efficacy of therapeutic treatment programs.
Objective: The work addresses mobile games’ potential as empirical assessment tools for cognitive processes within the domains of attention, recognition, recall, and memory applied to game strategy.
Methods: Two games have been developed with this objective. WarCAT is based on a familiar card game, War, and “Lock Picking” is a search for an optimal score, akin to finding the combination that opens a lock. Both games provide players with immediate feedback but engage different algorithms and heuristics to solve the respective problems at hand.
Conclusions: By collecting player data on large scales to allow for baseline establishment of cognitive abilities across demographic (age) profiles, longitudinal performance of individuals and of groups can be established, and from there, the potential exists to employ machine learning methods to detect subtle changes in an individual’s cognitive processes over time.
cognitive assessment, machine learning, health, mobile games
Abbreviations
ANN: Artificial Neural Network; BCI: Brain-Computer Interfacing; CNN: Convolutional Neural Network; ML: Machine Learning; MCI: Mild Cognitive Impairment; ROC: Receiver Operating Characteristic; RL: Reinforcement Learning; WarCAT : War Cognitive Assessment Tool.
Mild cognitive impairment (MCI) constitutes a clinical entity differentiated from healthy control subjects and those with very mild Alzheimer’s Disease [1]. Early recognition of MCI and subtle changes to specific cognitive abilities that precede an MCI diagnosis has the potential to improve the efficacy of therapeutic treatment programs [2,3]. Currently, over 35M people worldwide live with dementia and that is expected to reach 115M by 2050, fueled by an aging population, as aging is the biggest risk factor for cognitive decline and dementia [4]. The negative impacts on the individual, family, and caregivers are significant. As disease-modifying treatments are discovered, early diagnosis will be essential to assist in introducing therapies that can slow the progression and maintain longer quality of life [5].
Mental health apps are part of a much larger mobile health (mHealth) space, and the work addresses mHealth apps’ potential as empirical measurement tools for cognitive assessment including memory, learning, problem-solving, and other executive processes. The work finds clinical relevance in the early identification of cognitive decline, crucial for optimal pharmacological treatment and timely provision of psychosocial care [3,5-9]. The first symptoms of cognitive decline may be present several years before a clinical diagnosis of dementia can be made and thus tools that detect underlying patterns of brain dysfunction are of great importance.
This work combines mHealth with MCI assessment. This work goes beyond developing electronic/mobile presentations or reproductions of existing MCI assessment instruments; rather, the work presents mobile games that inherently provide a cognitive assessment function via the analysis of an individual’s game-playing data.
Clinicians indicate that standard MCI assessment instruments (non-electronic) can, at times, induce anxiety in the individual who knows they are being tested and may become frustrated at their self-perception of performance on the assessment. While there is a significant market of gamification of cognitive stimulation (“brain games” like Lumosity 1), there is currently little gamification of MCI assessment as one means to address this anxiety [10,11].
Gamification of MCI assessment also open up opportunities to collect player metadata on large scales that allow for baseline establishment of cognitive abilities across demographic (age) profiles, longitudinal performance of individuals and of groups, and from there, the potential to detect subtle changes in an individual’s cognitive processes over time. It is the self-perception of losses of specific cognitive processes such as recognition and recall that can cause anxiety to individuals being assessed. The proposed tools have been designed to include the ability to objectively assess recognition of a game strategy, recall of the strategy, failure to maintain set (reverting to a different strategy or no strategy at all), and perseveration (reverting to an earlier strategy).
The games as potential assessment tools are designed to be very simple, and the two games outlined below are exemplars of a genre of tools that have the inherent potential to provide data on cognitive functions. One is based on a familiar card game, War. In this variant, a person plays iteratively against a bot (computer) that is playing a consistent strategy. The person is provided immediate feedback of each round of play, allowing them to learn a winning strategy through reinforcement learning. Play continues against the bot until the person has demonstrated that they have won by more than chance, at which point the player "levels up" to continue. In the next level, the bot consistently plays a new strategy. By the stochastic nature of the game itself, there is opportunity for distraction, facilitating temporary lapses of concentration or memory. As all moves are tracked, there is an opportunity to analyze play in considerable detail via the metadata, essentially tracking “memory slips” in real time. The second game is an analogy to opening a barrel-type combination lock. In this game, rather than recognizing and countering a consistent strategy, the player is challenged to come up with a strategy to open a combination lock with play-by-play feedback of how close they are to “picking” the lock. Both games provide real-time data related to a person’s play.
WarCAT framework
WarCAT (War Cognitive Assessment Tool) is one of the games developed. The following is a description of the game and how it can be used as a cognitive assessment tool with qualitative as well as quantitative outputs.
The underlying algorithmic problem is more complicated than a search and is more closely related to the problem of sorting. Sorting is part of many computer as well as human problem-solving methods. Overall, people do need to learn sorting generally, and most acquire that ability early on in their cognitive development. People are reasonably good at sorting, although more likely akin to selecting an item from the unsorted group followed by insertion into a sorted group. For example, with respect to playing cards, many people have varied techniques or implicit algorithms that work well with small numbers of cards. The reason most approaches work well is the small problem instance size (N, the number of cards), and if one were to analyze the complexity of the algorithms a person used to sort them, there would be little difference as we are nowhere near an asymptotic limit.
The framework for WarCAT takes the form of a mobile game, an unexplored genre for MCI assessment. In addition to being mobile, it is also concurrent (head-to-head) and competitive. In its present state, each game consists of five rounds of the card game War, each game played is measured in seconds, and feedback is near instantaneous. Presently, three levels of a minimum of 100 games each have been implemented in the prototype, and the human player plays against a bot. The bot maintains a constant strategy for at least 100 games, and only after a player has demonstrated that they have beaten the bot by a non-chance margin can the player ‘level up’.
WarCAT combines real time player behavioural measures captured via metadata (e.g. play by play moves, duration played, duration per move, number of moves needed to level up, etc.) as well as self-report measures. The basic gaming framework has been further developed during the summer 2017 to optionally include more traditional cognitive assessments such as a paired associated learning test as an in-app feature which the player completes to proceed.
Figure 1 shows a screenshot of the proof of concept, which is currently rudimentary but functional. The registration screen illustrates the demographic data requested (optionally).
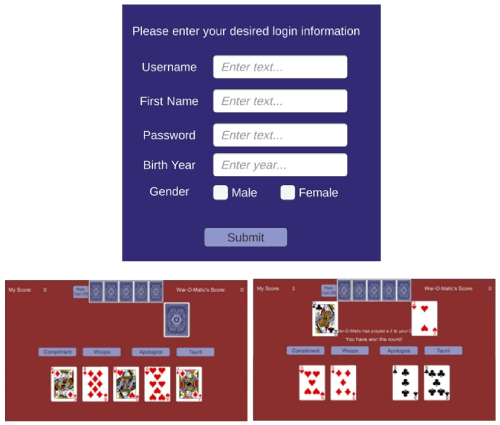
Figure 1. Example play of WarCAT
During play, the user is provided immediate feedback as to having won or lost the game (Figure 2). Figure 3 illustrates the feedback provided to a player when the player has beaten the bot by more than chance (statistically).

Figure 2. An example of feedback per round (reinforcement learning)
Also illustrated (Figures 3) is the aggregate strategy that the player played. For this instance, the person played mid-level cards followed by low cards followed by their high cards. This corresponds to the strategy they recognized early in the level, in which the bot consistently played low-high-medium cards. As the game collects extensive hand-by-hand data, one can infer a person’s ability to learn their winning strategy as well as periods where they may have forgotten their strategy or had difficulty in arranging their cards for play. This type of ordering cards presents challenges, even more so as one’s cards are selected at random.

Figure 3. An example of successfully beating the bot through three strategies. More Fun: Fireworks and a Dancing Cat (Dancing Cat not yet implemented)
WarCAT: Opportunities in data analysis
Visualizing a trajectory of learning a winning strategy would be very difficult. However, by virtue of the fact that the game is stochastic, there is opportunity to analyze a player’s behavior through the use of the corresponding confusion matrix and Receiver Operating Characteristic (ROC) curves for classification. Fig. 4 illustrates data collected per hand. It illustrates a phase of learning and forgetting and recall or relearning. Figure 4 provides a fingerprint of a person’s play suitable as input into a classifier.
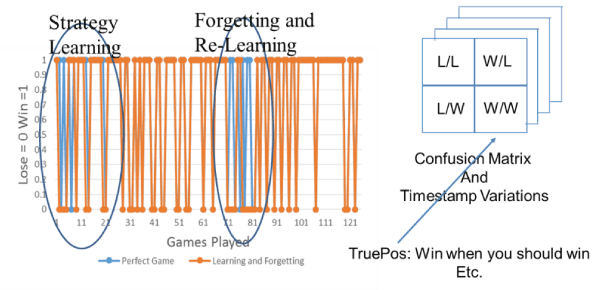
Figure 4. Illustration of data collected through a whole level of play
The research challenge is in using player metadata for analysis in confusion matrices, ROC curves, and clustering and/or classification of play through machine learning (ML) techniques. Once sufficient data are collected, an artificial neural network (ANN) can be trained with the data to classify the degree to which a person experiences cognitive difficulty during play. Another benefit is being able to monitor play behavior longitudinally. The ML classifier would be set up as follows. Initially bots will play against bots. During play, by virtue of the stochastic nature of the cards being dealt, a given hand will either be a true positive (Win when one should win as well as lose when one should lose) in contrast to the case where one would lose even though they played their winning strategy (i.e. dealt bad cards).
Specifically, Figures 4 and 5 illustrate a fingerprint of a person’s play (in this case, RDM). The differences in color for brief periods illustrated where RDM’s strategy varied from the optimal. The evidence is somewhat anecdotal as RDM would experience long periods of having learned and implemented the strategy, followed by periods of “memory slip”. These fingerprints would be used in a classifier to attempt to group differences in play.
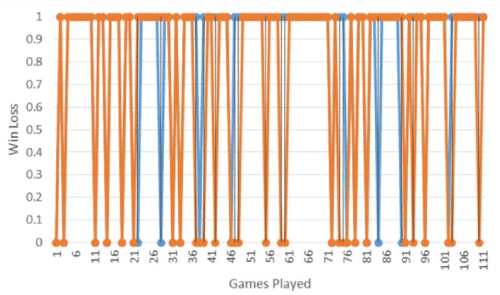
Figure 5. An example of real data collected and indications when “loss of set” was encountered.
A challenge to ML analysis is that currently, data are only labeled with a person’s age and gender which they agree to provide when registering to play (Figure 1), designed explicitly as minimal and non-invasive data to collect. The objective is to have a sufficient number of people of all ages and of healthy cognitive function play to be able to correlate play behavior to age and potentially to gender.
A perfect game by a “player” bot would be consistently playing the winning strategy against the “house” bot. For example, if the house bot were consistently playing low to high, the player bot would sort their cards and play them in an offset to the house bot. If the house bot played their lowest card first, the player bot would play their second lowest card, etc. With this scenario the probability of winning a 5 card hand is approximately 66%. This is confirmed semi-analytically as follows:
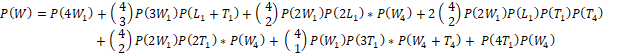
X1 represents Win, Loss, or Tie on cards 1 through 4, and X4 represents Win, Loss, or Tie on card 5. This calculation estimates a hand-winning probability of 0.66. At present, the data logging is set to play 100 hand epochs and the person advances to the next level if they win 60 of those hands. It may be preferable to have the person play any number of hands and have them level up once they win 60 hands (which may occur in fewer or greater than 100 hands overall). This may facilitate an easier classification of players of various ages and cognitive abilities. An easy feature to extract in this case would be the number of games required to “level up”.
With a large enough player base, a classifier should be able to classify a number of profile groups. At the highest level, the ML ANN should be able to easily differentiate between a real person and a bot and then sub-classify the person into various profiles. These may be categorized along profiles such as age and background collected over time with real players, or correlated with self- or independent cognitive assessments. Upon seeing a new player, the ML ANN can generalize to indicate the class of greatest correlation or belonging. This may be useful if, for example, a person of age 50 gets classified to a cohort group of otherwise healthy 70-year olds with normal age related memory issues.
A more sophisticated scoring system is also being developed, assigning greater rewards for narrow victories as opposed to lopsided victories. For each card played within a hand, the score would have calculated as ± (13- (PlayerCardVal- BotCardVal)) depending upon whose card was of greater value. Although this scoring system is statistically more difficult to win against, it provides the opportunity for a person to respond differently after seeing the bot’s first card played. Simulated probabilities of playing a winning strategy consistently against the bot are approximately 0.63. This strategy also opens the opportunity to potentially evaluate conservative vs. aggressive winning strategies (e.g. minimize loss vs. maximize gain). This allows us to enter into another area of ML- reinforcement learning (RL)-which is conjectured to be more closely aligned to how people learn and adapt than other areas of ML.
Figure 6 illustrates differences in perfect play using a winning strategy for bot vs. bot, for the two scoring mechanisms above. A histogram of scores per hand for weighted scoring is illustrated in Figure 7.
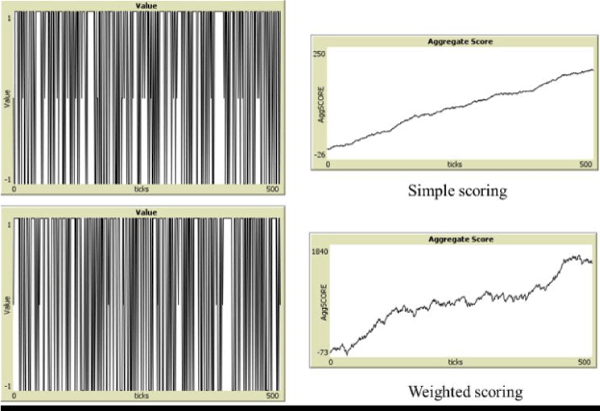
Figure 6. Typical “fingerprints” of Win-Loss Record and Aggregate Scoring from Simple and Weighted Scoring.
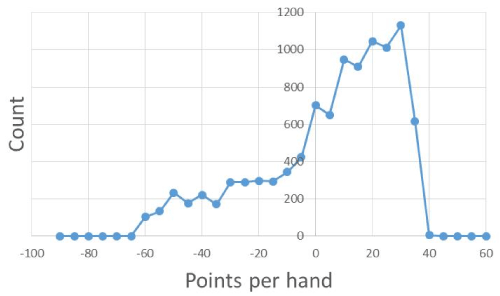
Figure 7. Score per Hand Histogram with Weighted Scoring
The histogram was generated from 10,000 games of bot vs. bot with one bot (the player bot) consistently playing a winning strategy against the house bot. An opportunity lies in a person’s ability to learn from the environment and alter their policy to mitigate against large losses. This is analogous to the ML technique associated with Reinforcement Learning and the cliff-walker problem where a more conservative solution may guard against a large but rare loss on average. The simple scoring vs. the weighted scoring is also interesting from the perspective of how people may feel or perceive their success in the game, as the nature of gains is more sporadic, and this can possibly mislead one into believing in winning and losing streaks. There are also considerably fewer ties in the weighted scoring system.
Table 1 illustrates a preliminary pilot for testing an early version of the game using weighted scoring. The purpose of the pilot was simply to gain feedback on game hedonics. It is interesting to note the variability in records: U1 was RDM, the oldest of the group who coincidentally corresponded to taking longer to “level up”.
Table 1. Player records of prototype test volunteers
User |
Level 1 |
Level 2 |
Level 3 |
|
win |
loss |
win |
loss |
win |
loss |
U1 |
142 |
53 |
220 |
74 |
292 |
101 |
U2 |
70 |
30 |
|
|
|
|
U3 |
85 |
12 |
160 |
34 |
219 |
50 |
U4 |
80 |
16 |
|
|
|
|
U5 |
69 |
28 |
208 |
87 |
|
|
U6 |
80 |
19 |
162 |
35 |
256 |
51 |
U7 |
75 |
26 |
|
|
|
|
U8 |
76 |
23 |
149 |
50 |
213 |
83 |
It is notable that the cognitive “fingerprints” of RDM and an age 20-something were considerably different. The question arises, “Do they reflect normal age related cognitive changes?” Possibly, and that only once sufficient data is collected and analyzed would one be able to tell. The eventual goal would be for ML-aided classification to serve as a giant funnel for people at risk, providing a basis upon which to seek more traditional clinician-mediated assessment and subsequent therapeutic or psychosocial care. Ideally the research will result in reaching a significant number of participants upon which to build baseline cognitive “fingerprints” across demographic profiles from which anomalies can be identified.
WarCAT: Technical considerations
WarCAT has been developed using Unity for the front end, a custom Java middle tier server and a MySQL backend data repository. Some of the technical challenges with developing these types of games is that WarCAT is in constant communication with a server that is logging all player actions. In effect, this makes the game a thin client as it is important that the server have complete knowledge of all hands dealt and how individual cards are played in order to eventually analyze data for subtle changes associated with strategy recognition, recall, loss of set, and perseveration.
An Android version of the game is available and accessible by contacting the corresponding author. As modifications and suggestions are being incorporated in an ongoing development fashion, WarCAT is not available on GooglePlay at this time. An iOS version is also being tested at this time. When stable, both will be released for download.
It is worth noting that WarCAT includes the capability to embed self-report survey questions and embed validated mental health assessment methods such as associated word pairings, to ultimately correlate player statistics with electronic reproductions of more traditional measures of mental health assessment. Although not implemented at this time, aspects of assessment methods such as those found in MoCA and the MMSE can be tailored for a mobile device as well.
“Lock Picking” Framework
Beyond memory and recall, problem-solving is one of the cornerstones of higher level cognitive functioning. Often guided by guesses and hunches, there is usually method to the madness. For discussion purposes here, the process of searching for an optimal or near-optimal solution is the problem under consideration.
In this case, the search problem of interest is akin to a guided search. For example, when searching for a word in a dictionary, very few people start at the beginning and proceed until they find the word they are looking for. If that were the case, dictionary words would be arranged in random order. More typically, people try to home in on a solution guided by rewards, hunches, and heuristics such as divide and conquer.
As a precursor to implementation on a mobile device, a simple game was developed in NetLogo to visualize how an algorithm or a person traverses a search space. While NetLogo is not a game development platform but rather an agent based modeling platform, it allows instances of play to be simulated and visualized very quickly.
Paraphrasing Einstein, the game should be as “simple as possible but no simpler”, in order that the game is easy to play while still potentially illuminating prodromes of potential cognitive impairments. Although the game is search-based, it may find a more receptive audience if it is considered a hunt for something, akin to opening a barrel-based combination lock such as the one illustrated below (Figure 8).
Figure 8. Barrel-type combination lock
The combination lock metaphor needs to be extended here to include a degree of feedback each time a person has guessed a number. The situation is more analogous to a professional lock-picker who by feel or sound knows when they are getting closer to picking the lock, or a child’s game of Hot and Cold. That is, feedback is provided so that a person knows when they are getting closer to opening the lock.
As this is a game that will need to be played iteratively, the combination needs to be resettable, the number of tumblers varied, and the number of numbers per tumbler varied. As such, the underpinning of the game is an extension to two-player games such as the Prisoner’s Dilemma-i.e. a two-player concurrent game played in an iterative fashion. For a game prototype, the following payoff matrix is currently being used, but others would suffice equally well (Figure 9).

Figure 9. The payoff matrix
The interpretation of this particular payoff matrix is as follows. If the player chose row 2 and the opposing player selected column 1 then the payoff for the first player would be 1 (matrix element indexed by [2,1]). The objective for this particular game is for the player to choose 3 rows against an opponent who selects 3 columns respectively such that they maximize their reward on aggregate of 3 selections of rows. This particular matrix was selected as it has a non-obvious reward or energy surface but can be solved with any hill climbing or gradient based method. Three rows selected per play facilitates traversing a 3 dimensional space of solutions which is useful in visualization. Furthermore, a player’s trajectory is viewed as traversing a three-dimensional cube of 4 x 4 x 4 vertices. This is equivalent to a barrel combination lock of three tumblers with options of selection a 1, 2, 3, or 4 as the value for any tumbler.
For purposes of visualization of learning an optimal solution or strategy, a person would play against a bot or machine. The bot would iteratively play the same three columns until the lock is opened and the person would attempt to obtain the maximum score possible in the fewest moves not knowing what columns the bot had selected. This is equivalent to trying to open a lock with a fixed combination.
“Lock Picking”: Three search strategies
The first “algorithm” is simply guessing: If the maximum reward is not attained, then guess again. This may be an approach used by a young child who is just developing their problem-solving skills. As a first example to illustrate play, a bot selects columns 1 2 3, for the duration of the game and the search algorithm (guessing) simply guesses until the optimal (maximum score is attained). The initial guess is a random vertex on a 3-dimensional cube of size 4 × 4 × 4 as shown in Figure 10.
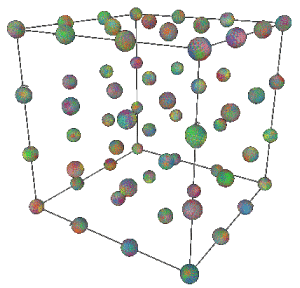
Figure 10. Initial Random Guesses (uniform)
After the initial guess, the player would traverse the cube searching for the optimal solution. Each vertex of the cube has an associated reward which is a function of the numbers selected. Figure 10 shows the results of 1000 random guess trajectories. Since this was a random search, the search space is uniformly explored (Figure 11).

Figure 11. 1000 trajectories of a random search
Running the simulation 1000 times, the average number of guesses to reach the maximum score converges to 32 as there are two optimal solutions in this situation (out of 64) where the bot had selected columns 1, 2, and 3. A single trajectory of 34 random guesses is shown in Figure 12.
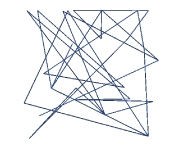
Figure 12. An isolated random search trajectory with multiple visits to the same vertex (34 edges).
Two adjacent optimal vertices were selected as equivalent maxima to limit the complexity of the search, as the eventual objective is to see how real people solve this type of problem while not making it too difficult. This is still a convex upward reward or energy surface. The reward surfaces of this type are easily created when the game is cast as a two-player game with some restrictions on the payoff matrix. As a game to help visualize how a person develops or learns a strategy, the payoff matrix approach also facilitates multiple tumblers with multiple numbers per tumbler. For trajectory visualizations, it is instructive to keep the search in a three-dimensional space.
As mentioned, this problem was selected to represent a search space that has two equivalent adjacent optima as well as reward function that has no local optima. The reason for this was to allow any gradient decent (ascent) algorithm or heuristic to find the optimal solution. That is, a simple greedy algorithm would never get stuck in a local optima.
As an illustration, the reward surface for a two-dimensional version using the same payoff matrix is shown in Figure 13. Here the bot selected columns 1 and 2 and the player would also be constrained to select only 2 rows. This surface would correspond to a two tumbler combination lock.
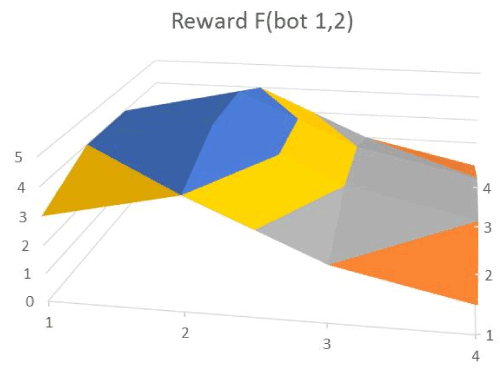
Figure 13. Reward surface with no local maxima.
A similar surface with no local optima applies to the case when three rows are selected with the bot playing columns 1, 2, 3. The total number of combinations that are selectable by the bot is 4 × 4 × 4=64. A matrix that would satisfy a single maxima is shown in Figure 14. The convenience of a payoff matrix is simply for ease in changing the cost surface if desired.

Figure 14. A payoff matrix with a single maxima
The second algorithm considered is a simplified variant of Tabu search where a player would not revisit a node that was already visited. This variant is slightly more intelligent than a random search and is essentially selecting without replacement. It is analogous to a problem solving strategy that a person may employ in solving a combination lock. Figure 15 illustrates 1000 trajectories from simple Tabu search. Although not apparent, it is slightly less dense that that of the random search of Figure 11. The random search trajectories of Fig. 10 had 32,000 edges whereas the Tabu search trajectories of Figure 15 has 21,800 edges.

Figure 15. 1000 trajectories of Tabu search
Figure 16 illustrates an isolated trajectory of an average Tabu search. Here no vertices are visited more than once.
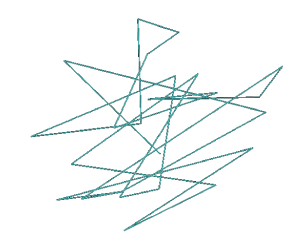
Figure 16. An isolated Tabu search trajectory with no vertices visited more than once (25 edges)
Tabu search is essentially searching without replacement. As analogy, the expected number of steps taken until one hits upon the optimal is the same as the number of balls one would take from an urn containing 2 blue balls from among 62 red balls if one were trying to select a blue ball. The expected number of trials in this case is 21.6. This approach - although simple - is not likely an approach that one would try as it does require precise memory of previous guesses or equivalently vertices visited. A person is more likely to recall the reward as opposed to maintaining a list of vertices visited.
The third algorithm to consider in searching for maximum score (analogous to opening the combination lock) is slightly more sophisticated in that it implements gradient ascent, where the value of the reward is used as immediate feedback in making decisions. Gradient ascent, as a person may implement it, would be to select a starting vertex at random or at a corner and then optimize along one direction in isolation at time. In general this process would typically find and become stuck in a local optima, unless one considers the cube a toroid (one that wraps around in all three dimensions as a tumbler on a barrel type lock would). In general, this strategy works best if there is only one global optima.
Figure 17 illustrates the third search algorithm (greedy gradient ascent) for 1000 trajectories. The pattern of searching is considerably more ordered in comparison to the random walk or Tabu search. The two balls illustrate positions of optimal ascent for this particular bot strategy.
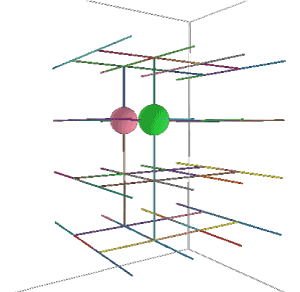
Figure 17. 1000 trajectories of gradient ascent search.
The number of edges in the graph of Figure 17 is 13,100 (many overlap). The average walk through the space is approximately 13.1 steps with an isolated trajectory illustrated in Figure 18 (14 steps).
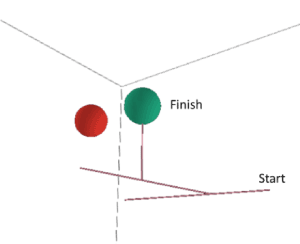
Figure 18. An isolated gradient ascent search trajectory with limited backtracking (15 edges)
This gradient ascent algorithm essentially optimizes in one direction at a time. As the reward surface is concave upward, this will always allow the player to reach the optimal vertex. Payoff matrices can easily be constructed such that the surface has multiple local optima as well as global optima whereby a person would have to employ even more sophisticated methods to continue their search if stuck in a local optima as illustrated in Figure 19. In these cases, the person would need some type of probabilistic backtracking to get out of a local maxima.
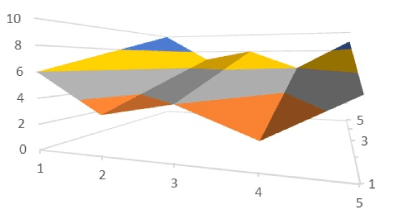
Figure 19. A reward surface with multiple optima
The surface shown on Figure 19 is where the bot had selected the following two columns from a (5 × 5) payoff matrix. In this case, the payoff matrix was not doubly stochastic and did not result in a single optima as can be seen from the elements of column 2.
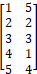
Here the gradient ascent strategy would often get stuck at a local optima. For each of the two rows selected the number of options is from 1 to 5, hence the surface covers a 5 × 5 grid in area (two tumblers five numbers each).
Figure 20 illustrates several real trajectories from persons with sound cognitive abilities. Although the data is limited to a few people, it is already apparent that people use a combination of gradient ascent enhanced with some degree of backtracking based on their memory of previous rewards and vertices visited.
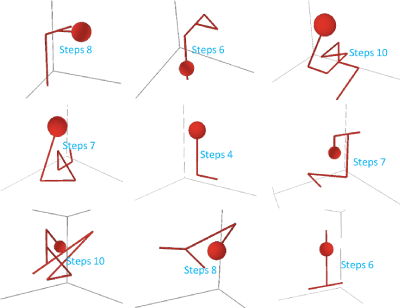
Figure 20. Trajectories taken by real players
As an alternative means of tumbler setting, one could use the following procedure. If one were setting a tumbler with x positions, numbered 1 through x. with x representing the maximum score of the tumbler, the following pseudocode would ensure one global maxima with no local maxima.
- Assign value x to index i = random [0,x-1]
- Assign value x-1 to index random [(i+1)modi or (i-1)modi]
- Assign value x-2 to index available [(i+1)modi or (i-1)modi]
- Assign value x-3 to index random [(i+2)modi or (i-2)modi]
- Assign value x-4 to index available [(i+2)modi or (i-2)modi]
- Etc.
This procedure ensures that independent of the number of tumblers or numbers per tumbler, the solution space has only one global maxima and no local minima.
Like the WarCAT game, the “Lock Picking” game also carries the potential to gather player metadata across many players on each move made. This can be used in ML approaches to cluster and classify player strategies, illustrated by the chosen trajectories through the search space, both by individual and by group, and both by instance and longitudinally. Data analysis can focus on measures of cognitive functions within the domains of attention and memory, assessing the extent to which a player appears to be choosing and then maintaining a strategy in their play.
2021 Copyright OAT. All rights reserv
“Lock Picking” android implementation
An example of an implementation of the “lock picking” app within an Android Smartphone is illustrated in Figure 21. This is more visually appealing than the description above and illustrates the type of data collected.
Figure 21. Instantiation of the “lock picking” game and data recorded.
In this example, the person started with a reasonably high score and guided by their strategy, proceeded to open the lock in 12 tries. The virtue of these games is their stochastic nature and repetition. Nothing can be inferred from one game played or in this case, from one lock picked. Once a person opens a lock, a new cost surface would be created and the person attempts to open the lock once again. A person should fairly soon develop a strategy or algorithm and use it to open any lock provided. Challenges can be to vary the number of tumblers as well as the cost surface in more subtle ways. The payoff matrix used here was very simple:
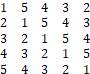
Similar to fingerprinting for MCI assessment in WarCAT, a sequence of plays in the lock picking application provide a fingerprint of a person’s ability to reason, develop strategy, and retain or recall strategy which is amenable to machine learning. This type of data is illustrated in Figure 22. As the selection of attempted lock combinations and a person’s score are tracked, the data will contain instances of confusion as well as instances of systematic or algorithmic play (Figure 22).
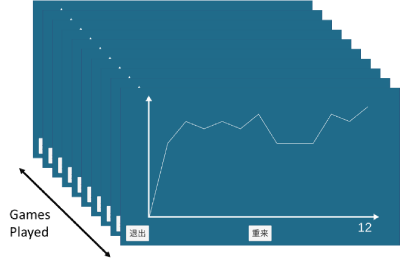
Figure 22. Data collected of a person’s play over several rounds.
A MATLAB image representation of a fingerprint is shown in Figure 23.
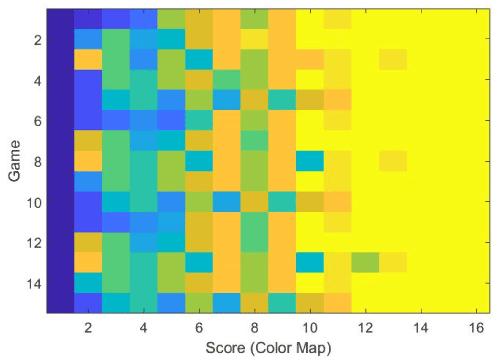
Figure 23. A “fingerprint” image of a person’s play after 15 games played.
This type of data, although not human-friendly, is very well suited to machine learning techniques such as Convolutional Neural Networks (CNNs) that excel at classifying images. There is a complication that arises with this type of classification, that being that the data needs to be labeled. Labels we have at this time are limited to those associated with meta-data a person provides when they download and install the app. Ideally, this game data should be collated with assessments, which although technically feasible would require a crowdsourced or community data collection effort (Table 2).
Table 2. Contrasting Algorithmic approaches with Cognitive Thought processes
Search Method |
Average steps (1000 Runs) |
Random |
32 |
Tabu |
21.8 |
Gradient Ascent |
13.1 |
People |
<10 as shown in Figure 20 |
As an additional note regarding serious games such as these, they can be quite easily made language agnostic. Figure 21 the game is in Chinese.
The first game presented, WarCAT, is fairly well developed as a mobile game with emphasis on assessment of the cognitive functions of recognition (learning a strategy) and recall (applying that strategy consistently) to the gameplay. The game itself is fairly complex as one of the underlying algorithmic problems is sorting, compounded by requiring card ordering that is not necessarily monotonic. That is, a person may have to order cards medium, high, followed by low. The interesting unexamined conjecture of the game is the very stochastic nature of the game itself may induce a memory slip or sufficient confusion because even when the winning strategy is played, one can still lose if one simply has been dealt a bad hand of cards in relation to the bot’s hand. This allows us to build confusion matrices and use methods such as ROC curves to classify player behavior. Additionally, data collected during play can serve as input to a ML algorithm to facilitate classification, potentially identifying subtle cognitive changes and deterioration.
The second game, “Lock Picking”, compared computational strategies for a simple search for a maximal value analogous to finding the combination to open the lock. Three computational algorithms were presented with increasing degrees of sophistication: random walk, followed by simple Tabu search, followed by a gradient ascent on a reward surface that was convex. These computer models were visualized by their trajectories though a three-dimensional space. This was then contrasted to a limited number of trials where cognitively health individuals were tasked with solving the same problem and their trajectory tracked. Not surprisingly, a human player outperformed the relatively deterministic algorithms implemented, and it is reasonable to infer that a ML approach would likely perform in a comparable manner to a human. Tracking the search space trajectories of a large number of players can build a database of strategies of both healthy and impaired individuals, correlated to functions of attention and memory. Iterative challenges are possible as the number of tumblers increased and the number of selections changed to increase complexity. The bot can also change its selection to modify the reward at a given level, and the payoff matrix can be changed to introduce local maxima that have to be navigated while searching for the global maximum.
In addition to the “Lock Picking” and WarCAT games, the opportunities exist to gather other data such as event timing, data from the accelerometer, and data from the front facing camera of the mobile device. These data can provide additional information on how a person is playing a game, including potential difficulties while selecting cards or turning tumblers. The analogy with traditional assessment instruments is that clinicians administering a test may notice, for example, an unusually strong grip on a pencil when performing a drawing a simple shape. In this case, the grip (ancillary to the task) provides as much data to the clinician as the actual shape drawn (the main task). In the case of mobile devices, eye-tracking technologies using front-facing cameras may provide additional insights into how a score is achieved. Although this work considers only simple mobile games with no additional hardware requirements, it is also worth mentioning the role Brain Computer Interfacing (BCI) technology may play in cognitive function assessment during game playing.
WarCAT and “Lock Picking” are simple exemplars of a genre of games that have the potential to provide the research community with a tool to examine the relationship between cognitive function and aging. It will provide clinicians with an additional tool for identifying potential pre-symptomatic cognitive decline through long-term game-interaction data collection, complementing traditional instruments currently in use and potentially allowing measurement of multiple cognitive domains. The mobile game is designed to be an engaging activity for users, and potentially less intimidating than other dementia screening methods typically administered by family physicians and other health care providers. The collected data will offer an opportunity to better understand the relationship between normal memory inefficiency and age, ultimately leading to better statistical models and follow-on insights into pre-symptomatic dementias and other cognitive impairments.
The key technology innovation is in the gamification of cognitive assessment (as opposed to the simple reproduction of traditional assessment tools in electronic or mobile formats), or the application of Smartphone instruments to the assessment of various cognitive functions related to learning, retention, attention, and memory applied to game strategy. These benefits will be achieved through the use of statistical models and more advanced analytic methods (machine learning) as data collection methods and volume improves. Once validated, the work can be integrated into much larger aging related initiatives and toolsets.
Authors Leduc-McNiven, White, Zheng, and McLeod designed and developed the apps. Authors McLeod and Friesen designed the implementation and evaluation strategy. Authors McLeod and Friesen prepared the manuscript. Prototype app development was funded under Natural sciences & Engineering Research Council of Canada grants 397751-12 to author Friesen and 6712-12 to author McLeod.
None declared.
- Petersen RD, Smith GE, Waring SC, Ivnik RJ, Tangalos EG, et al. (1999) Mild cognitive impairment: Clinical Characterization and outcome. Arch Neurol 56: 303-308. [Crossref]
- Jack CR, Holtzman DM (2013) Biomarker modeling of Alzheimer’s disease. Neuron 80: 1347-1358. [Crossref]
- Spaan PEJ (2016) Episodic and semantic memory impairments in (very) early Alzheimer’s disease: The diagnostic accuracy of paired-associate learning formats. Cogent Psychology 3: 1125076.
- World Health Organization (WHO) and Alzheimer's Disease International, Dementia: A Public Health Priority.
- Prince M, Bryce R, Ferri C (2011) World Alzheimer Report 2011: The benefits of early diagnosis and intervention. Alzheimer's Disease International.
- Tong T, Chignell M, Tierney MC, Lee J (2016) A serious game for clinical assessment of cognitive status: validation study. JMIR Serious Games 4: e7. [Crossref]
- Hagler S, Jimison HB, Pavel M (2014) Assessing executive function using a computer game: Computational modeling of cognitive processes. IEEE J Biomed Health Inform 18: 1442-1452. [Crossref]
- Jimison H, Pavel M (2006) Embedded assessment algorithms within home-based cognitive computer game exercises for elders. In Engineering in Medicine and Biology Society, 2006. EMBS'06. 28th Annual International Conference of the IEEE: 6101-6104.
- Basak C, Voss MW, Erickson KI, Boot WR, Kramer AF (2011) Regional differences in brain volume predict the acquisition of skill in a complex real-time strategy videogame. Brain Cogn 76: 407-414. [Crossref]
- Thompson O, Barrett S, Patterson C, Craig D (2012) Examining the neurocognitive validity of commercially available, smartphone-based puzzle games. Psychology 3: 525
- Manero B, Torrente J, Freire M, Fernández-Manjón B (2016) An instrument to build a gamer clustering framework according to gaming preferences and habits. Computers in Human Behavior 62: 353-363.