Background: Quantum chemistry, i.e., density functional theory-based molecular modeling (DFT/MM) using computer software of “Spartan” on personal computer is a novel analysis method for equilibrium geometry and energy structure of van der Waals force (vdW) aggregates of molecules. In view of the action of preventing disease, DFT/MM is undertaken to analyze redox reactions in mitochondria (mt) as battery of cells which is functioning using oxygen and D-glucose.
Materials and methods: DFT-based molecular modeling (DFT/MM), equivalent to the quantum mechanics/molecular mechanics (QM/MM) method, was performed by using the B3LYP exchange-correlation function and the 6–31G(d) basis set with Spartan’16 (Wavefunction, Inc. Irvine, CA).
Results: DFT/MM verifies and predicts that superoxide radical anion (O2.-) and hydrogen peroxide (HOOH) are produced by redox reactions of ground state oxygen (3O2) and D-glucose in mt. Without exhausting ATP, accumulation of HOOH will start in mt, resulting in production of hazardous hydroxyl radical (HO dot). The hydroxyl radical (HO dot) destroys cellular membrane, leading to dysfunction of mt. Accumulation of HOOH and formation of hazardous HO radical will be suppressed by antioxidative chemical substance, e.g., Vitamin C, thyroxin (T4), and triiodothyronine (T3). Thyroid hormone is one of so-called super oxide dismutase, iodine atoms in which play an important role of antioxidative effects in mt.
Conclusion: Dietary intake of antioxidative chemical substance like Vitamin C, preservation of acceptable level of iodine-bearing T4 and T3 in blood, and aerobic exercise which prevents accumulation of HOOH are essential for prolonged mt as battery of cells.
density functional theory, mitochondria, superoxide radical anion, hydrogen peroxide, hydroxyl radical, Vitamin C, thyroid hormone, triiodothyronine (T3) and thyroxine (T4)
Living cells whose numbers ranges from 4∼6 x 1013 is connected by 1011 m long blood vessel. For healthy longevity, all cells must function with sustainability in lifespan. The healthy function of living cells is maintained by biological energy of adenosine triphosphate (ATP) which is produced in mitochondria (mt) as chemical battery of cells. Wikipedia mentions that the number of mt in a cell can vary widely by organism, tissue, and cell type. For instance, red blood cells have no mitochondria, whereas liver cells can have more than 2000. To our knowledge, heart cells, which is always beating, are full of mt in cells. Accordingly, function of mt as batteries of cells must be durable, and dysfunction of mt leads to aging, disease and death. Considering redox reactions in production of ATP from oxygen and D-glucose in mt, and importance of antioxidative enzyme and coenzyme as anti-aging supplements, we speculate that so-called hazardous active oxygen must concern with dysfunction of mt.
On the other hand, recent outstanding progress of computational quantum chemistry, i.e., density functional theory-based molecular modeling (DFT/MM) enable experimental scientists to analyze, verify and predict equilibrium geometry and electron energy structures of molecular aggregates induced by van der Waals forces (vdW).1~10) In order to understand importance of antioxidative effects on mt, DFT/MM is undertaken to analyze what are oxygen species in mt, how are they produced in mt, what happen to mt when such active oxygen species are accumulated in mt, and how does Vitamin C and iodine-bearing thyroid hormone, i.e., triiodothyronine (T3) and thyroxine (T4) contribute to healthy life.
DFT-based molecular modeling (DFT/MM), equivalent to the quantum mechanics/molecular mechanics (QM/MM) method, is carried out by using the B3LYP exchange-correlation functional and the 6–31G(d) basis set with Spartan’16 (Wavefunction, Inc. Irvine, CA).
Verification of reactive oxygen species in mt
Mitochondria (Mt)’s main job is to carry out the redox phosphorylation to ATP using oxygen and D-glucose:
3O2 + D-glucose => O2.- => ATP + CO2
In view of quantum chemistry, air oxygen is regarded as triplet state oxygen (3O2). Carbon dioxide (CO2) is final product from oxidation of D-glucose probably via citric acid cycle.
Quantum chemistry molecular modeling, i.e., density functional theory-based molecular modeling (DFT/MM) verifies redox reaction as shown in Figure 1.
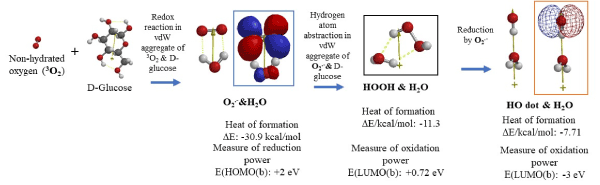
Figure 1. DFT/MM-based analysis for equilibrium geometry and energy structures of hydrated superoxide radical anion (O2.-&H2O), hydrated hydrogen peroxide (HOOH&H2O), and hydrated hydroxyl radical (OH dot&H2O) which may form from vdW aggregates of oxygen (3O2) & D-glucose
DFT/MM reveals that water molecule H2O has a strong tendency to aggregate with each other and other molecules through hydrogen bonding (one of van der Waals forces) (Table S1), and the case is true in cells. Figure 1 shows DFT/MM-determined equilibrium geometry structures of 3O2, D-glucose, hydrated superoxide O2.-, hydrated hydrogen peroxide, HOOH, and hydrated hydroxyl radical (HO dot). They are formed via vdW aggregation with D-glucose in mt, giving hydrated O2.-, which has powerful reduction potential (EHOMO(b)=+2 eV) and will be consumed for production of energetic adenosine triphosphate (ATP). It is worth noting that hydrated HO dot is verified and predicted to have powerful oxidation potential (ELUMO(b)=-3 eV), and HO dot forms via electron transfer (reduction) to oxidant HOOH. The formation of HO dot will lead to oxidative destruction of mt membrane.
Detail of their formation and followed reactions is depicted in Figure 2, which are based on DFT/MM of active oxygen species and their vdW aggregates with D-glucose (Tables S2, S3, S4, S5 and Figure S1). Importantly, all heat of formation of vdW aggregates is negative, i.e., exothermic.
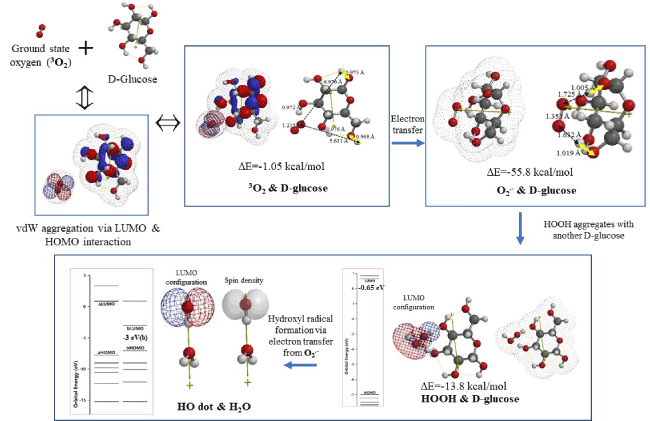
Figure 2. DFT/MM-based analysis for formation, and equilibrium geometry and energy structures of vdW aggregates of 3O2 &D-glucose, O2.-&D-glucose, HOOH&D-glucose and HOdot&H2O
The ground state oxygen (3O2) interacts with D-glucose via LUMO-HOMO interaction, giving a vdW aggregate of 3O2 & D-glucose. Heat of formation for the equilibrium structures (DE=-1.05 kcal/mol) predicts that the vdW aggregation is not strong, but the LUMO configuration locates on 3O2 and HOMO on D-glucose on the aggregate 3O2 & D-glucose (Table S4). Then, the 3O2 undergoes highly exothermic electron transfer (DE=-55.8 kcal/mol) from HOMO to LUMO, being converted into superoxide radical anion of O2.-. The case is true for vdW aggregate of 3O2 with fully hydrated D-glucose which we speculated in H2O-full living systems (Table S4).
DFT/MM further validates that the energy structures of O2.- and the hydrated one have remarkable reduction potential, EHOMO(b), 2.0~4.2 eV, which is positive enough for reductive phosphorylation to ATP production. In addition, the vdW aggregate of O2.- & D-glucose has a tight vdW aggregate structure, i.e., two O-H bonds of O2.- & D-glucose elongate when compared to those of 3O2 & D-glucose, and the O-O bond of oxygen molecules also elongates from 1.215 Å (3O2 & D-glucose ) to 1.337 Å (O2.- & D-glucose). In other words, the equilibrium geometry of vdW aggregate of O2.- & D-glucose has a convenient structure for production of HOOH (Figure S1).
The hazardous HOOH will be formed when superoxide radical anion (O2.-) are not consumed continuously for production of ATP. To make matter worse, HOOH will be converted to hydroxyl radical by reductive electron transfer from O2.-, giving hydrated hydroxyl radical (HO dot & H2O) in the vicinity of mt (Figure 2).
The vdW aggregate of HO radical (HO dot) with D-glucose will result in degradation of D-glucose through abstraction of hydrogen atom of O-H bond in the D-glucose (Table S5). HOOH and hydroxyl radical (HO dot) may increase in concentration in living cells when ATP is not consumed well. Lack of muscular movement, lack of aerobic exercise, and losing physical fitness may cause accumulation of HOOH which prevent healthy longevity.
DFT/MM-based verification of membrane disruption caused by accumulation of HOOH and hydroxyl radical (HO dot).
We could speculate that healthy longevity will be maintained by continuous production of ATP in every living cell. In other words, unhealthy aging must come from decline in quality of mt in cells, and the decline of mt quality must come from accumulation of hydrogen peroxide and subsequent hydroxyl radical in the vicinity of mt.
In order to clarify what happens when HOOH and hydroxyl radical are survived during aging, two kinds of vdW aggregates of n-dodecane, (n-C12H26)2 and of n-dodecanoic acid (lauric acid) (n-C11H23COOH)2 are constructed as models of lipid bilayer membrane. The former represents hydrocarbon parts of lipid bilayer (Table S6) and the latter bilayer model of (n-C11H23COOH)2 represent carboxylate parts of lipid bilayers (Table S7).
Interestingly, heat of formation (DE) for the former (n-C11H23COOH)2 model is -0.05 kcal/mol, predicting that vdW aggregation is in equilibrium state, compared to the later (n-C11H23COOH)2 model whose heat of formation is DE=-10.6 kcal/mol.
Figure 3 shows equilibrium geometry of van der Waals aggregates of bilayer model, (n-C12H26)2 with hydrogen peroxide (HOOH) and with hydrated hydroxyl radical (HO dot&H2O). HOMO of (n-C12H26)2 interacts with LUMO of HOOH gives vdW aggregate of HOOH&(n-C12H26)2. However, the electron density structure of HOOH&(n-C12H26)2 remain unchanged, and both HOMO and LUMO configurations stay on HOOH part. These analyses predict that HOOH will be adsorbed on alky chain in bilayer membrane, being easily converted to hydroxyl radical. The equilibrium geometry structure of vdW aggregate of HO dot&H2O&(n-C12H26)2 shows that hydroxyl radical abstracts hydrogen atom on the alkyl group, forming H2O and alkyl radical as verified by the extended C-H bond, 2.117Å.and the localization of the spin (radical) density on the alkyl chain. The structural and energetic structure changes predict destruction of membrane structures by hazardous hydroxyl radical.
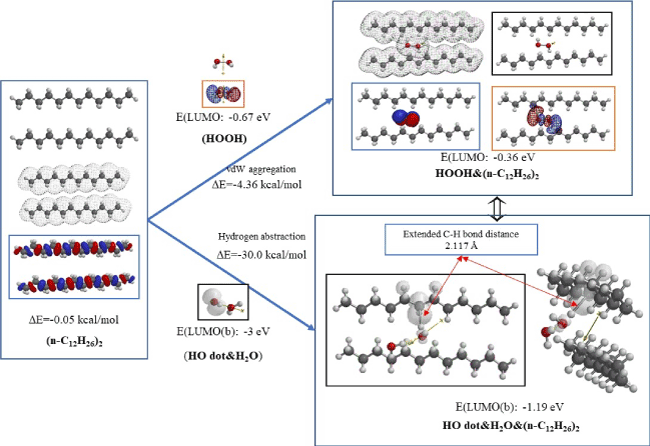
Figure 3. Equilibrium geometry analysis for vdW aggregates of bilayer model of (n-C12H26)2 with hydrogen peroxide (HOOH) and with hydrated hydroxyl radical (HO dot&H2O)
As for the bilayer model of (n-C11H23COOH)2, not only hydroxyl radical but also hydrogen peroxide (HOOH) lead to destruction of membrane structures. Figure 4 shows equilibrium geometry of vdW aggregates of (n-C11H23COOH)2 with hydrated hydrogen peroxide (HOOH&H2O) and, with hydrated hydroxyl radical (HO dot&H2O). The bilayer model of (n-C11H23COOH)2 locates HOMO on carboxylic acid group. DFT/MM analysis verifies that vdW aggregation of HOOH with the carboxyl group results in large structural change. In addition, HOOH on the membrane model can be a source of hydroxyl radical since LUMO locates on hydrogen peroxide on HOOH&H2O &(n-C11H23COOH)2.
The vdW aggregation with hydroxyl radical (HO dot) results in formation of H2O from hydroxyl radical and radical of n-C10H23CH (dot)COOH as verified and predicted by the extended α-C-H bond distance, 4.422 Å and the localization of spin (radical) density on α-carbon atom of the bilayer model (Figure 4). DFT/MM-based analysis also indicates that the powerful oxidation potential, ELUMO(b): -3 eV, is the same as that of hydrated HO dot, ELUMO(b): -3 eV.
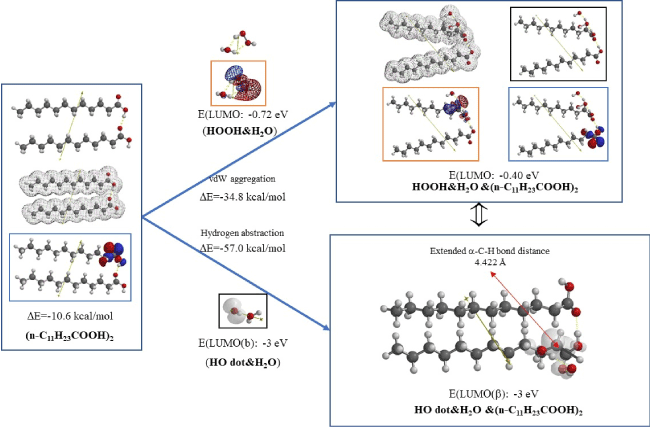
Figure 4. Equilibrium geometry analysis for vdW aggregates of bilayer model of (n-C11H23COOH)2 with hydrated hydrogen peroxide (HOOH&H2O) and with hydrated hydroxyl radical (HO dot&H2O)
We have now validated that the accumulation of HOOH occur on mt membrane, and the vdW aggregation of HOOH at carboxyl group of mt lipid bilayer induces destruction of the membrane. Mt dysfunction will start as the destruction of the membrane proceed.
Verification of antioxidative effects of Vitamin C and iodine-bearing thyroid hormone.
Wikipedia mentions that, Vitamin C is a vitamin found in various foods and sold as an antiaging supplement as an antioxidant, and Vitamin C is an essential nutrient involved in the repair of tissue. However, pharmacological effects and anticancer effects are still argued among physicians. In addition, thyroid hormones are chemical substances, triiodothyronine (T3) and thyroxine (T4). They are speculated to be released from the thyroid gland and detected to be in the range of 0.8~1.7 ng/ml for T4 and 2.1~3.1 pg/ml for T3 by blood examination. They are considered now responsible for regulation of metabolism of cells.
DFT/MM analysis predicts that both Vitamin C and thyroid hormone, T3 and T4 have excellent antioxidative effect on HOOH and hydroxyl radical (Tables S8, S9, S10).
Figure 5 shows that hydrated hydrogen peroxide (HOOH&H2O) interact with Vitamin C via LUMO-HOMO interaction, giving vdW aggregate of HOOH&H2O &Vitamin C with exothermic heat of formation (DE=-26.0 kcal/mol). Interestingly, neither LUMO nor HOMO locates on HOOH. This means that oxidation reaction sites move to Vitamin C, and then Vitamin C-stabilized HOOH could not be converted into hydroxyl radical (HO dot). The resulting radical from Vitamin C has high oxidation potential, ELUMO: -0.58 eV, which is more negative than that of hydrated HOOH (ELUMO: +0.72 eV), supporting antioxidative effects of Vitamin C to HOOH.
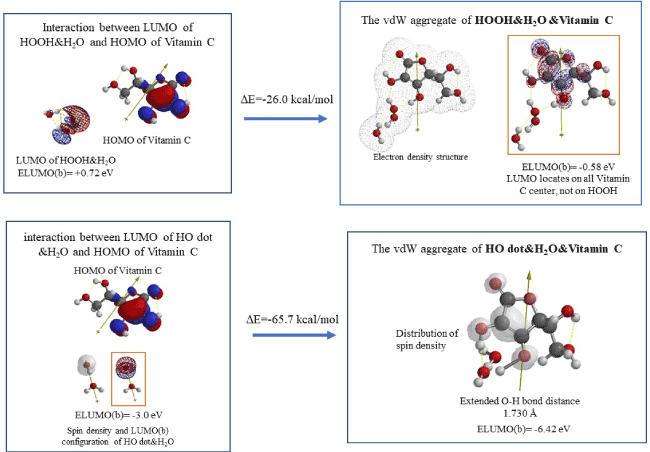
Figure 5. DFT/MM-based analysis for antioxidative effects of Vitamin C
In addition, Vitamin C undergoes exothermic reaction (DE=-65.7 kcal/mol) with hydroxyl radical, and hydroxyl radical (HO dot) abstracts hydrogen atom, being converted into H2O as validated by the extended OH bond distance of 1.730 Å. The resulting Vitamin C radical has oxidation potential, ELUMO: -6.42 eV, more negative than that of hydroxyl radical, but the localization of spin (radical) density on Vitamin C may decrease oxidation power and hydrogen abstraction power of the radical.
DFT/MM-based analysis is now extended to thyroid hormone for their antioxidative effects. Figure 6 shows that hydrated hydrogen peroxide (HOOH&H2O) interacts with T4 via LUMO-HOMO interaction, giving the vdW aggregate of HOOH&H2O &T4 with exothermic heat of formation (DE=-22.5 kcal/mol).
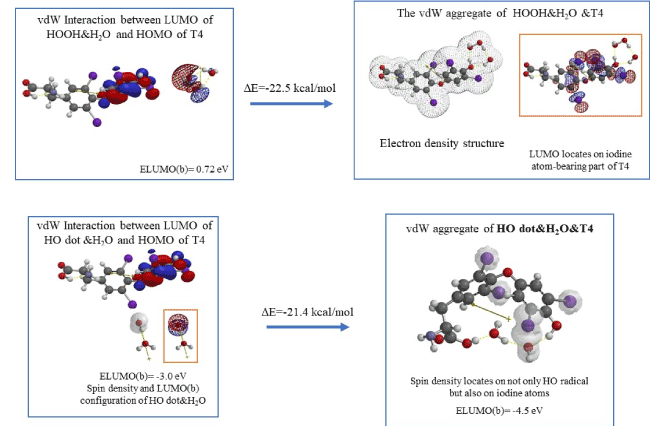
Figure 6. Density functional theory-based analysis for antioxidative effect of T4
It is interesting to note that as observed for Vitamin C, neither LUMO nor HOMO locates on HOOH and, interestingly LUMO locate on iodine atoms-bearing part of T4. The analysis predicts that redox reaction sites moves from HOOH to the iodine atom-bearing T4. In other words, T4 works as antioxidant to HOOH, and HOOH could not be converted into hazardous hydroxyl radical (HO dot).
DFT/MM also verifies that T4 undergoes exothermic reaction (DE=-21.4 kcal/mol) with hydroxyl radical (HO dot), and, interestingly the spin density on HO dot delocalizes on four iodine atoms in T4. In addition, no extended bond distance is observed. The oxidation potential of ELUMO(b-spin) of HO dot&H2O&T4, ELUMO: -4.5 eV is lower than that of HO dot&H2O of ELUMO: -3.0 eV (Figure 6). However, the delocalization of spin (radical) density to iodine atoms must contribute to antioxidative effects of T4 as discussed in the case of Vitamin C. In addition, the antioxidative effects of T4 must be durable compared to that of Vitamin C. As for T3, the durable antioxidative effect is comparable to that of T4 (Table S9, Figure S2). Iodine-bearing thyroid hormone may be one of powerful superoxide dismutase.
DFT/MM for human longevity validates that (1) superoxide radical anion (O2.-) is produced quickly and consumed for ATP production in mt during high quality of life. (2) Without exhausting of ATP during ageing, accumulation of O2.- will start to abstract hydrogen atom from molecules like D-glucose, becoming hazardous HOOH. (3) Gradual HOOH accumulation will lead to production of hydroxyl radical. (4) The hydroxyl radical destruct cellular membrane structure. (5) Accumulation of hazardous HOOH and subsequent hydroxyl radical will result in advance of aging of cells. (6) Dietary intake of antioxidative chemical substance like Vitamin C followed by preservation of acceptable level of iodine-bearing T4 and T3 in blood, and aerobic exercise which prevents accumulation of HOOH are essential for mt sustainability as powerhouse of cells.
We are continuing cooperative research for antioxidative effects for mt in view of preventing integrative molecular medicine.
View Supplementary Data
- Frithjof C Kpper, Martin C Feiters, Berit Olofsson, Tatsuo Kaiho, Shozo Yanagida, et al. (2011) Commemorating two centuries of iodine research: An interdisciplinary overview of current research. Angew Chem Int Ed Engl 50: 11598-11611. [Crossref]
- Shozo Yanagida, Kazuhiro Manseki, Hiroshi Segawa (2015) Theoretical evaluation of electron transport in aniline tetramer-based dye-sensitized solar cells. Electrochim Acta 10: 179-169.
- Shozo Yanagida, Susumu Yanagisawa, Hiroshi Segawa (2015) Molecular orbital-based verification of conductivity of tetramethylammonium pentaiodide and pentaiodide-based electrolytes in dye-sensitized solar cells. J Electrochem Soc 162: E263-E270.
- Anubhav Jain, Yongwoo Shin, Kristin A Persson (2016) Computational predictions of energy materials using density functional theory. Nature reviews | materials 1: 1-13.
- Susumu Yanagisawa, Taiga Yasuda, Kouji Inagaki, Morikawa Yoshitada, Kazuhiro Manseki, et al. (2016) Intermolecular interaction as the origin of red shifts in absorption spectra of zinc-phthalocyanine from first-principles. J Phys Chem 57: 2526-2533
- Shozo Yanagida, Susumu Yanagisawa, Masatoshi Yanagida, Hiroshi Segawa (2017) Computational verification of so-called perovskite solar cells as PbI64--aligned solar cells. J Electrochem Soc 164: E3598-E3605.
- Kang Jiang, Xi Cheng1, Xinyi Cai1, Shozo Yanagida, Jiangbin Xia (2017) Exploring novel poly(thiophene-3-yl-amine) through facile self-acid assisted-polycondensation. Polymer Chemistry 55: 4003-4012.
- Shozo Yanagida, Susumu Yanagisawa, Koichi Yamashita, Ryota Jono, Hiroshi Segawa (2017) Molecular-orbital-based verification of water photo-splitting on Pt-loaded TiO2: Effective formation of HOOH and reduced platinum cluster as precursors of O2 and H2, ECS Trans 80: 1091-1112.
- Shozo Yanagida, and Takeko Matsumura (2018) Computational verification of radio and MW frequency heating using density functional theory. AMPERE Newsletter 95: 27-32.
- Shozo Yanagida, Susumu Yanagisawa, Masatoshi Yanagida, Hiroshi Segawa (2018) Validity of density functional theory-based molecular modeling for UV/visible spectroscopy and the rationale of panchromatic PbI6 4-(MeNH3+)4-structured molecular solar cells. Jpn J App Phys 57: 121602-1-121602-8.






