Additive manufacturing (AM) of NiTi parts by selective laser melting method is emerging as a widespread technique for implant and biomedical applications. With SLM, it is possible to fabricate complex porous parts with tailored shape memory and material properties (e.g elastic modulus, ductility, transformation stress, strain). In this study, NiTi samples with three distinct periodic geometrical structures (i.e., Schwartz, Diamond, and Gyroid) were fabricated by SLM and their morphological, mechanical and shape memory properties were systematically characterized. It was revealed that porous NiTi SMA can show the recoverable strain of 7% with low Young’s Modulus and their properties can be adjusted with porosity characteristics.
shape memory alloys, NiTi, additive manufacturing, selective laser melting, porous structures, triply periodic minimal surface
In recent years, Nickel-Titanium (NiTi) shape memory alloys (SMAs) have been acknowledged as the most promising biomaterial for the use in bone implants because they present superelasticity (SE) similar to that of human bones [1-5], and most importantly, they demonstrate close-to-bone stiffness (i.e., E, modulus of elasticity) [6-10]. In general, a bone-like stiffness for the implant is crucial as it allows the normal stress distribution from the implant to the bone in a normal pattern and hence reduces the risk of implant failure resulting from stress shielding effect [11-13]. While solid NiTi (E ≈38 GPa) decreases stiffness over conventional biomaterials, such as steel (E ≈193 GPa) or grade 5 titanium (E ≈112 GPa), it is useful to further reduce the equivalent stiffness of dense NiTi to the level of cortical bone, which is in the range of 17.6-31.2 GPa, through the introduction of porosity topologically (i.e., the geometry of the device) during implant design and fabrication [14]. It is worth noting that pores also allow the ingrowth of bone and body fluid transfer in the implant, and hence produce a firmer fixation implant while being well nourished [15-18].
Amongst different porous structures, the triply periodic minimal surfaces (TPMS) have been recognized as a versatile method of achieving biomorphic porous implant designs [19]. TPMS parts are categorized by their zero-mean curvature at every point and are the subset of the larger class of constant mean curvature (CMC) surfaces. These lattice-type structures best mimic the nature of bone as they are continuous through space, are periodic in three different directions, demonstrate bone-like mass transport properties, and partition the space into two sub-spaces by a nonintersecting two-sided surface [20,21]. Schwartz-type, Diamond-type, and Gyroid-type are the most favorable TPMS structures. Due to the complexity of TPMS structures, they have been only realized through additive manufacturing (AM) techniques through the introduction of porosity into the CAD 3D models [11, 22-24]. There are several studies on fabrications of TPMS structures through using different AM techniques (e.g., Selective laser melting (SLM), electron beam melting (EBM).
Bobbert et al. [25] studied the mechanical behavior and fatigue life of Ti-6Al-4V SLM TPMS structures, in particular, Diamond-type and Gyroid-type, having porosity level up to 71%. They observed a unique combination of relatively low elastic modulus (as low as 3.2 GPa) in the range of trabecular bone, a high yield stress (92–276 MPa) exceeding that of cortical bone, a bone-level permeability (0.05-6.1×10−. m2), and a high fatigue limit (as high as 60% of yield stress). Yan et al. [19] evaluated the manufacturability of Ti-6Al-4V SLM TPMS structures of Diamond-type and Gyroid-type with higher porosity level (∼80-95%) and pore size (480-1600 μm), which ultimately showed modulus elasticity of 0.12-1.25 GPa. They observed orthogonally oriented martensite α′ laths with the width of 100–300 μm. They also observed the microhardness in the range of 3.71±0.35 GPa. Kadkhodapour et al. [26] studied the failure mechanism of Ti-6Al-4V SLM TPMS structures of I-WP30-type, I-WP45-type, F-RD45-type with 55-70% porosity and 5000 μm pore size. They observed bilateral layer-by-layer failure due to the buckling of micro-struts for I-WP while observed global shearing bands for F-RD-type. They reported the Young modulus of 2168-2809 MPa for I-WP and 2520 MPa for F-RD. Ataee et al. [27] fabricated Gyroid samples with 82-85% of porosity and pore size of 2000-3000 μm with the same material, but EBM method. They observed orthogonally orientated martensite α′ needles in columnar grains along the building direction. They also reported the hardness of 3.89 GPa and modulus of elasticity of 0.6-1.1 GPa for the fabricated parts. It should be noted that the smaller pore sizes in the range of 250-500 µm are more desirable in terms of osseointegration and vascularization [28]. Hrabe et al. [29] studied the Ti-6Al-4V EBM TPMS structures of Diamond-type with 60-83% porosity and 50-1500 μm pore size. They reported that energy density has an effect on the strut size, which has to be optimized to mimic that of the CAD file.
Speirs et al. [22,30] were the only group investigated the behavior of AM NiTi TPMS structures. They suggested using low laser power (P) and low scanning speed (v) to decrease the level of geometrical deviation. This limitation is due to a required minimum distance for the laser to deliver the required performance. Then, they developed a formula (v (mm/s)=1317*v (mm)) that relates the minimum distance required for the laser to reach the desired scanning speed [22]. In another study, they have focused on the fatigue behavior and failure mechanisms of Ni50.1Ti (at.%) SLM TPMS structures of octahedron-type, Gyroid-type, and sheet Gyroid-type with porosity level up to 80%. Their results demonstrated high dependency of the fatigue life of the samples to the geometry of the fabricated TPMS parts, where the sheet Gyroid-type displayed the best fatigue life as high as 30% of yield stress [30].
The present study is the first attempt to systematically investigate the mechanical properties and shape memory response of NiTi TPMS. To this aim, we fabricated porous Ni50.1Ti (at.%) parts with different pore morphologies but with the same level of porosity using an SLM method. The pore’s structure was changed through using three types of TPMS structures: Diamond-type, Gyroid-type, and Schwartz-type.
Mathematical description and geometric modeling of TPMS
The nodal approximations of the P, D, and G are taken from a study by Von Schnering and Nesper [31] and are represented in equations 1, 2, and 3, respectively. Constant K effectively controls the porosity level (PL) of the resulting lattice structures. The relationship between K and porosity level is unique for each TPMS.
f(x) = cos(2πx)+cos(2πy)+cos(2πz)-K (1)
f(x) = sin(2πx)sin(2πy)sin(2πz) + sin(2πx)cos(2πy)cos(2πz) + cos(2πx)sin(2πy)cos(2πz) + cos(2πx)cos(2πy)sin(2πz)-K (2)
f(x) = cos(2πx)sin(2πy) + cos(2πy)sin(2πz) + cos(2πz)sin(2πx)-K (3)
To represent the TPMS as the nodal surface, the coordinates of each given surface were created using K3dSurf v0.6.2 software (Figures 1A-C). Then, Geomagic Studio 12 (3DSystems, Rock Hill, USA) was used to recreate the surfaces, which serve as the boundary between solid and void material and to generate solid structures (Figures 1D-F).
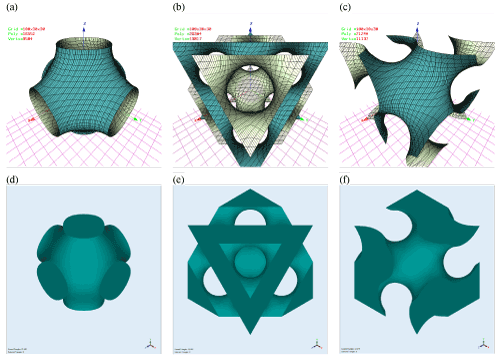
Figure 1. The coordinates of each given surfaces and solid structures are generated for (a), (d) Schwartz; (b), (e) Diamond; and (c), (f) Gyroid TPMS
For Schwartz, Diamond, and Gyroid, porosity level can be reasonably approximated in the range of 0.1 to 0.9 with the linear equations described below.
PLP = 28.742K + 49.998 (4)
PLD = 42.284K + 50.12 (5)
PLG = 32.783K + 50.118 (6)
Open porous cubic scaffolds with 9 mm height, 9 mm length, and 9 mm width were designed with the constant porosity level of 69.27%. The assigned values for K were assigned as 0.67, 0.45, and 0.58 for Schwartz, Diamond, and Gyroid, respectively. For compression testing purpose, two plates with the thinness of 1.5 mm were added to the top and bottom of each cellular structure.A total of 3 samples of each design were generated. Figure 2 demonstrates the structure of the compression samples related to Schwartz, Gyroid, and Diamond.

Figure 2. . Three types of CAD files (Top) and SLM fabricated NiTi parts (Bottom), (a) Schwartz, (b) Gyroid, and (c) Diamond
Fabrication and experimental procedures
Ingots of Ni50.1Ti49.9 (at. %) were purchased from Nitinol Devices & Components, Inc. (Currently known as Confluent Meical, Fremont, CA) and were gas atomized using TLS Technik GmbH & Co (Bitterfeld Germany) using Electrode Induction-melting Gas Atomization (EIGA) method. Afterward, powder particle was sieved to the size of 25-75 μm and used for SLM fabrication. PXM by Phenix/3D Systems, equipped with a 300 W Ytterbium fiber laser, was utilized for the SLM fabrication.The laser power, scanning speed, layer thickness, and hatch spacing were 250W, 1250 mm/s, 30 μm, and 120 μm respectively. The transformation temperatures before reported in our previous study [32] where the austenite start and finish temperatures were 69 and 100ºC and martensite start and finish temperatures were 73 and 39ºC, respectively.
Compression tests were conducted using the 100 kN MTS Landmark servo-hydraulic test platform. All samples were loaded from 5 MPa and the load was incrementally increased until the samples were failed. During loading, a strain rate of 10-4 sec-1 was utilized. An MTS high-temperature extensometer was attached to the grips to measure the strain. Mica band heaters retrofitted to the compression grips were used to heat up the specimens and cooling was performed through internal liquid nitrogen flow in the compression grips.K-type thermocouples measured the temperature and controlled by using Omega CN8200 Series PID temperature controller. Tests occurred at a cooling rate of 4°C/ min and a heating rate of 5°C/min. In order to align the data, the temperature and strain results were recorded at the same time in each second by PID and MTS condolers, respectively.
Morphological properties
Table 1 demonstrates the morphological properties of these unit cells which were extracted from CAD files (top) and SLM fabricated parts (bottom) of Figure 2. The pore size was the diameter of the best-fitted circle inside the pore channel [27,28] which was shown with the red circle in Figure 2. The pore size showed a decreasing trend, while the number of pores had an increasing trend from Schwartz to Diamond structures. These trends had a direct impact on the mechanical behavior and fracture of specimens which explained in the next section. Among these structures, the Diamond with the pore size of 324 µm was a more suitable option for applications as bone substitute materials [28]. In order to calculate the porosity levels of fabricated samples, the density and mass of the parts were measured to achieve the actual volume (V1) of structures. After measuring the dimensions of the samples and by assuming the parts as a solid cube, the solid volume (V2) of structures were calculated. Finally, the porosity levels were obtained by ((V2-V1)/V2) ×100. Although the impact of geometry on the porosity level of fabricated samples was neglectable (around 1% difference was observed among three structures), SLM fabrication process decreased the porosity level of the structures around 10%. This difference can be attributed to the melting of more powders during the fabrication of the unit cells, thus, larger than expected struts were made, shrinking the porosity level.
Table 1. Overview of the morphological properties of each unit cell given from the CAD designs (Top) and SLM fabricated samples (Bottom)
CAD Designs |
Unit cell types |
Porosity level (%) |
Unit cell size (mm) |
Pore size
(µm) |
Schwartz |
69.27 |
3 |
1990 |
Gyroid |
69.27 |
3 |
1160 |
Diamond |
69.27 |
3 |
324 |
SLM Fabricated Samples |
|
Porosity level (%) |
Density (gr/cm3) |
Mass (gr) |
Pore size
(µm) |
Schwartz |
59.09 |
5.597 |
2.05 |
1855-1995 |
Gyroid |
57.88 |
5.754 |
1.97 |
1075-1229 |
Diamond |
58.26 |
5.601 |
2.25 |
294-441 |
Compressive test to fracture
The compressive stress-strain curves of the parts at 24 °C are displayed in Figure 3. Since the samples were martensite at this temperature, the initial elastic deformation of martensite was followed by martensite reorientation. Further loading resulted in an elastic deformation of oriented martensite and/or plastic deformation. Figure 3 proves that the mechanical properties were highly pore morphology dependent and despite having the same level of porosity, they each displayed unique responses, which is in good agreement with the literature [33]. Based on the failure response shown in Figure 3, the material properties of the samples are depicted in Table 2. The Schwartz Structure had the maximum elastic modulus (Em) of 16.9 GPa, while the Em of Gyroid and Diamond structures were 7 GPa and 6.4 GPa, respectively. In our previous study, the elastic modulus of the dense sample was determined as 69 GPa [32]. Therefore, Young’s Modulus was decreased by 76 % for Schwartz and 90 in Gyroid and Diamond when they were compared to the dense NiTi through the tailored the pore structures. It was observed that the Schwartz structure had the highest strength as it failed at a peak stress of 71.9 MPa with the strain of 7.7%. The Gyroid structure could endure a peak stress level of 34.7 MPa at 14.9%. The Diamond structure showed a similar response to that of the Gyroid with peak stress level of 26.5 MPa at 13.1%. Diamond and Gyroid samples endured the higher amount of plastic deformations than the Schwartz sample. This difference can be attributed to the fact that Schwartz structure had larger holes and more non-uniform cross-section than the other two structures. The pore size of Schwartz, Gyroid, and Diamond structures were 1990, 1160 and 324 µm (Table 1), respectively, thus, at the certain cross-sections of the Schwartz type, the area fraction of solid structure was lower than two others.Thus, the stress in those regions increased rapidly and the failure of one strut resulted in the failure of the whole structure. The Diamond structure had a higher number of pores with smaller sizes and had a uniform distribution of the pores that resulted in higher ductility.

Figure 3. Compressive stress-strain response of different SLM structures at room temperature
Table 2. Elastic Modulus, critical stress and maximum stress for the Diamond, Gyroid and Schwartz Geometries
Structure |
Elastic Modulus (GPa) |
Critical Stress (σs) (MPa) |
Maximum Stress (MPa) |
Diamond |
6.4 |
4.9 |
26.5 |
Gyroid |
7.0 |
5.8 |
34.7 |
Schwartz |
16.9 |
4.6 |
71.9 |
Dense |
69.0 |
180 |
1619.0 |
It should also be noted that the first plateau region where martensite reorientation took place significantly differs in these structures. In Schwartz, the slope of this region was much higher and the strain was much lower than the other two structures. The Diamond showed the lowest slope and highest strain in this region. The differences in the slope and strain showed that the shape memory response of these alloys also depends on the pore morphology.
A fracture is a break of material into pieces under the stress. Most of the time, the solid material fracture occurs due to the expansion of certain displacement discontinuity layers throw the sample. If a crack grows perpendicular to the direction of displacement, it is called a normal crack; if it develops tangentially to displacement direction, it is called a shear crack [34]. Based on the SEM study which our group did on the dense NiTi samples with similar compositions and fabrication parameters of TPMS structures, several types of defects were reported for SLM specimens. One of the more important ones was the existence of unmelted powders as an initial site for the appearance of cracks inside the specimens [4]. When the porosity introduces to a sample, the strut thickness has a direct influence on the strength and failure mechanism of structures. The thicker strut has higher bending resistance, causing the compressive stress to increase [35]. Figure 4 shows the images of the porous samples after the failure tests. When comparing these three structures, the Schwartz had the thickest and the lowest number of struts whereas the Diamond had the thinnest and highest number of struts, with the Gyroid in the middle. The failures were postponed until all the struts reached the maximum shear stress and the cracks were developed 45º to the max and min plane share stresses. So, the individual struts were failed one after another until whole structure was broken. For the Schwartz, although a higher stress was captured by thicker strut, a sudden rapture happened because of the existence of fewer struts (Figure 3). The existence of thinner struts in Gyroid and Diamond structures made them a more suitable option for lower stress applications with larger plastic deformation because of failing more struts along the developing cracks. The different type of failure modes clearly shows the strength and fracture mechanism of porous NiTi can be tailored by tailoring the porosity structure.

Figure 4. Images of the failed (a) Schwartz, (b) Diamond, and (c) Gyroid structures after mechanical testing
Shape memory effect
Results for the thermal cycling under constant compressive stress for each type of structure are displayed in Figure 5. To perform such experiments, at each cycle, the samples were loaded to selected stress levels at austenite state, and then thermally cycled between a temperature below Mf and above Af. After one complete cycle, the stress was increased incrementally and the thermal cycling was repeated for each stress level until the sample failed. Most of the samples were failed during transforming from austenite to martensite phases (during cooling). Transformation temperatures, recoverable, irrecoverable (IRS) and total (TS) strains, and temperature hysteresis can be obtained through this experiment using a graphical Tangent method [36]. The samples were failed under 20, 30 and 70 MPa for Diamond, Gyroid and Schwartz structures, respectively, which were close to the maximum stress levels reported in Table 2.

Figure 5. Thermal cycling under constant compressive load for the a) Schwartz, b) Diamond, and c) Gyroid structures
The TS, IRS and the transformation temperatures (Af and Ms) were extracted from Figure 5 and plotted as a function of applied stress in Figure 6. For all the structures, as the stress levels were increased, the Af and Ms were also increased. The Ms was 61.4 °C, 60.7 °C and 58.4 °C for Schwartz, Gyroid and Diamond structures at 5 MPa and increased to 71.3 °C, 73.9 °C and 72.19 °C at 15 MPa, respectively. In a similar fashion Af increased from 83.2 °C to 97.4°C for Schwartz, 84.3°C to 111.4 °C for Gyroid and 84.5 °C to 122.8 °C for the Diamond structure at 5 and 20 MPa, respectively. The results in Figure 6 illustrates that the relationship between stress and transformation temperatures is linear which satisfied the Clausius–Clapeyron (CC) equation, i.e. where Δσ, ΔT, and ΔH are the change in critical stress, temperature and transformation enthalpy, respectively, T0 is the equilibrium temperature and is the maximum transformation strain [37]. Based on this equation, the CC slopes for martensite start temperatures were 2.15, 0.52 and 0.62 MPa/ºC and for austenite finish temperature were 1.97, 0.35 and 0.26 MPa/ºC for Schwartz, Gyroid and Diamond structures, respectively. It should be noted that although the same nominal stress was applied to the samples (at higher stress levels), the transformation temperatures were different due to the difference in local stress distribution that governs the formation of martensite variants.

Figure 6. Applied stress vs. transformation temperatures of the Diamond, Gyroid and Schwartz structures
The volume fraction of oriented martensite initially increased with stress and then saturated. Moreover, plastic deformation increased with stress as well. Thus, the TS was expected to increase [9,38]. The Figure 7 shows that both TS and IRS increased with stress in structures. Although the Diamond and Gyroid have shown only the increasing trend for TS, the Schwartz growing trend was saturated after pass the 35 MPa. The saturation of TS indicates that the material reached the maximum transformation strain at about 35 MPa, which corresponds to the end of first plateau region shown in Figure 3. The Diamond and Gyroid did not show the saturation stress due to their low strength.
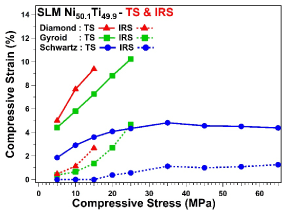
Figure 7. Total (solid line) and irrecoverable (dashed line) strain of the Diamond, Gyroid and Schwartz structures
The Diamond and Gyroid types showed higher IRS in comparison with Schwartz. The values for Diamond and Gyroid structures were 2.67% at 15 MPa and 4.67% at 25 MPa respectively. Whereas no IRS was observed up to 15 MPa of stress in Schwartz type, while maximum IRS was only 1.26% at 65MPa. The IRS was caused by plastic deformation and/or stabilized martensite. The IRS under 20 MPa was determined as 7.15, 6.11 and 3.69 % for Diamond, Gyroid and Schwartz types, respectively. These results were in good agreement with the observations from the first plateau region shown in Figure 3. Hence, it can be concluded that the Schwartz structure would be more suitable where fully recoverable phase transformation and higher strength is needed. On the other hand, the Diamond and Gyroid types would be suitable for the cases where high transformation strain is desired.
Although there is a vast amount of research on the additive manufacturing of TPMS structures out of Ti-6Al-4V, it is not the case for NiTi TPMS structures. To our knowledge, Speirs et al. [22,30] is the only group that reported mechanical properties of Gyroid type of SLM NiTi samples. They have reported a superior fatigue life of SLM NiTi Gyroid sample that displays SLM NiTi scaffolds can provide more suitable mechanical support within actual stress range values that can be seen in human bones.
The tissue engineering study showed that the primary step in designing an excellent functional scaffold is introducing geometry option, which is the main factor of its mechanical properties [21]. The TPMS geometries are one of the suitable structures for the design process of artificial bone scaffolds [39]. The Young’s modulus of cortical bone was measured to be from 10.4 to 18.6 GPa [40]. It is clear that the measured elastic moduli of 6.4 GPa for Diamond-type, 7 GPa for Gyroid-type, and 15.9 GPa for Schwartz-type are very close to the Modulus of bone. In a nutshell, mimicking the mechanical behavior of the bone as well as the inherent advantages of creating porous implants using TPMS structures (e.g. enhanced bone ingrowth and Osseo integration), make these NiTi structures desirable implants.
Selective laser melting was used to fabricate porous TPMS NiTi parts, and thermomechanical tests were conducted to characterize the mechanical and shape memory properties. The porosity level of these samples was kept constant at 69% while their geometric structure was altered. Three geometric structures were chosen, namely Diamond, Gyroid and Schwartz types. The SLM fabricated samples were shown around 59% porosity level, regardless of the geometry, which this decreasing can be related to the fabrication parameters. The mechanical properties of the porous samples were determined to be highly geometric structure dependent. The Schwartz type structure showed the highest recoverable strain at low-stress levels with low irrecoverable strains. Through the above experimentation, it can be inferred that the Elastic modulus of the SLM fabricated NiTi samples can be tailored and reduced by approximately 76-90 % by introducing a porous structure than the dense NiTi and further modifying the geometry of the porous structure. Base on the results, where fully recoverable phase transformation, strength, and resistance to plastic deformation are needed, the Schwartz type would be more applicable at low-stress levels, whereas the Diamond and Gyroid types would be suitable where greater transformation strains are desirable at low-stress levels.
This study received the financial support of a Technology Validation Start-Up Fund by the Ohio Third Frontier as well as Ohio Federal Research Network.
- Saedi S, Turabi AS, Andani MT, Haberland C, Elahinia M, et al. (2016) Thermomechanical characterization of Ni-rich NiTi fabricated by selective laser melting. Smart Mater Struct 25: 035005.
- Saedi S, Turabi AS, Andani MT, Haberland C, Elahinia M, et al. (2016) The influence of heat treatment on the thermomechanical response of Ni-rich NiTi alloys manufactured by selective laser melting. J Alloys Compd 677: 204-210.
- Saedi S, Turabi AS, Andani MT, Moghaddam NS, Elahinia M, et al. (2017) Texture, aging, and superelasticity of selective laser melting fabricated Ni-rich NiTi alloys. Mater Sci and Eng: A 686: 1-10.
- Moghaddam NS, Saghaian SE, Amerinatanzi A, Ibrahim H, Li P, et al. (2018) Anisotropic tensile and actuation properties of NiTi fabricated with selective laser melting. Mater Sci and Eng: A 724: 220-230.
- Moghaddam NS, Saedi S, Amerinatanzi A, Saghaian E, Jahadakbar A, et al. (2018) Selective laser melting of Ni-rich NiTi: selection of process parameters and the superelastic response, Behavior and Mechanics of Multifunctional Materials and Composites XII International Society for Optics and Photonics 105960W.
- Rondelli G (1996) Corrosion resistance tests on NiTi shape memory alloy. Biomaterials 17: 2003-2008. [Crossref]
- Shabalovskaya SA (2002) Surface, corrosion and biocompatibility aspects of Nitinol as an implant material. Biomed Mater Eng 12: 69-109. [Crossref]
- Andani MT, Haberland C, Walker JM, Karamooz M, Turabi SA, et al. (2016) Achieving biocompatible stiffness in NiTi through additive manufacturing. J Intell Mater Syst Struct 27: 2661-2671.
- Saedi S, Saghaian SE, Jahadakbar A, Shayesteh Moghaddam N, Taheri Andani M, et al. (2018) Shape memory response of porous NiTi shape memory alloys fabricated by selective laser melting. J Mater Sci Mater Med 29: 40. [Crossref]
- Moghaddam NS, Saedi S, Amerinatanzi A, Jahadakbar A, Saghaian E, et al. (2018) Influence of SLM on compressive response of NiTi scaffolds, Behavior and Mechanics of Multifunctional Materials and Composites XII. Intern Society for Optics and Photonics page. 105960H.
- Shayesteh Moghaddam N, Jahadakbar A, Amerinatanzi A, Elahinia M, Miller M (2016) Metallic fixation of mandibular segmental defects: Graft immobilization and orofacial functional maintenance. Plast Reconstr Surg Glob Open Open 4:e858. [Crossref]
- Jahadakbar A, Shayesteh Moghaddam N, Amerinatanzi A, Dean D, Karaca HE (2016) Finite element simulation and additive manufacturing of stiffness-matched niti fixation hardware for mandibular reconstruction surgery. Bioengineering (Basel) 3: 36. [Crossref]
- Moghaddam NS, Andani MT, Amerinatanzi A, Haberland C, Huff S, et al. (2016) Dean, Metals for bone implants: safety, design, and efficacy. Biomanufacturing Reviews 1: 1.
- H.J.B. J.A. Helsen, Metals as Biomaterials, Wiley, Baffins Lane, Chichester, England (1998).
- Elahinia MH, Hashemi M, Tabesh M, Bhaduri SB (2012) Manufacturing and processing of NiTi implants: a review. Prog Mater Sci 57: 911-946.
- Greiner C, Oppenheimer SM, Dunand DC (2005) High strength, low stiffness, porous NiTi with superelastic properties. Acta Biomater 1: 705-716. [Crossref]
- Chu C, Chung C, Lin P, Wang S, (2004) Fabrication of porous NiTi shape memory alloy for hard tissue implants by combustion synthesis. Mater Sci and Eng: A 366: 114-119.
- Bansiddhi A, Sargeant TD, Stupp SI, Dunand DC (2008) Porous NiTi for bone implants: a review. Acta Biomater 4: 773-782. [Crossref]
- Yan C, Hao L, Hussein A, Young P (2015) Ti–6Al–4V triply periodic minimal surface structures for bone implants fabricated via selective laser melting. J Mech Behav Biomed Mater 51: 61-73. [Crossref]
- Rajagopalan S, Robb RA (2006) Schwarz meets Schwann: design and fabrication of biomorphic and durataxic tissue engineering scaffolds. Med Image Anal 10: 693-712. [Crossref]
- Kapfer SC, Hyde ST, Mecke K, Arns CH, Schröder-Turk G (2011) Minimal surface scaffold designs for tissue engineering. Biomaterials 32: 6875-6882. [Crossref]
- Speirs M, Dadbakhsh S, Buls S, Kruth J, Van Humbeeck J, Schrooten J (2013) The effect of SLM parameters on geometrical characteristics of open porous NiTi scaffolds, High Value Manufacturing: Advanced Research in Virtual and Rapid Prototyping: Proceedings of the 6th International Conference on Advanced Research in Virtual and Rapid Prototyping, Leiria, Portugal, 1-5 October, 2013, CRC Press, 2013, p. 309.
- Ravari MK, Esfahani SN, Andani MT, Kadkhodaei M, Ghaei A, et al. (2016) On the effects of geometry, defects, and material asymmetry on the mechanical response of shape memory alloy cellular lattice structures. Smart Mater Struct 25: 025008.
- Esfahani SN, Andani MT, Moghaddam NS, Mirzaeifar R, Elahinia M (2016) Independent tuning of stiffness and toughness of additively manufactured titanium-polymer composites: Simulation, fabrication, and experimental studies. Jou of Mater Processing Tech 238: 22-29.
- Bobbert FSL, Lietaert K, Eftekhari AA, Pouran B, Ahmadi SM, et al. (2017) Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater 53: 572-584. [Crossref]
- Kadkhodapour J, Montazerian H, Darabi AC, Zargarian A, Schmauder S (2017) The relationships between deformation mechanisms and mechanical properties of additively manufactured porous biomaterials. J Mech Behav Biomed Mater 70: 28-42. [Crossref]
- Ataee A, Li Y, Fraser D, Song G, Wen C (2018) Anisotropic Ti-6Al-4V gyroid scaffolds manufactured by electron beam melting (EBM) for bone implant applications. Mater & Design 137: 345-354.
- Kujala S, Ryhänen J, Danilov A, Tuukkanen J (2003) Effect of porosity on the osteointegration and bone ingrowth of a weight-bearing nickel–titanium bone graft substitute. Biomaterials 24: 4691-4697. [Crossref]
- Hrabe NW, Heinl P, Flinn B, Körner C, Bordia RK (2011) Compression-compression fatigue of selective electron beam melted cellular titanium (Ti-6Al-4V). J Biomed Mater Res B Appl Biomater 99: 313-320. [Crossref]
- Speirs M, Van Hooreweder B, Van Humbeeck J, Kruth JP (2017) Kruth, Fatigue behaviour of NiTi shape memory alloy scaffolds produced by SLM, a unit cell design comparison. J Mech Behav Biomed Mater 70: 53-59. [Crossref]
- Von Schnering H, Nesper R (1991) Nodal surfaces of Fourier series: fundamental invariants of structured matter. Zeitschrift für Physik B Condensed Matter 83: 407-412.
- Taheri Andani M, Saedi S, Turabi AS, Karamooz MR, Haberland C, et al. (2017) Mechanical and shape memory properties of porous Ni 50.1 Ti 49.9 alloys manufactured by selective laser melting. J Mech Behav Biomed Mater 68: 224-231. [Crossref]
- Frenzel J, Zhang Z, Somsen C, Neuking K, Eggeler G (2007) Influence of carbon on martensitic phase transformations in NiTi shape memory alloys. Acta materialia 55: 1331-1341.
- Cherepanov GP, Balankin AS, Ivanova VS (1995) Fractal fracture mechanics—a review. Eng Fract Mech 51: 997-1033.
- Dadbakhsh S, Speirs M, Kruth JP, Van Humbeeck J (2015) Influence of SLM on shape memory and compression behaviour of NiTi scaffolds. CIRP Annals 64: 209-212.
- Kaya I, Karaca H, Souri M, Chumlyakov Y, Kurkcu H (2017) Effects of orientation on the shape memory behavior of Ni 51 Ti 49 single crystals. Mater Sci and Eng: A 686: 73-81.
- Karaca H, Saghaian S, Ded G, Tobe H, Basaran B, et al. (2013) Effects of nanoprecipitation on the shape memory and material properties of an Ni-rich NiTiHf high temperature shape memory alloy. Acta Materialia 61: 7422-7431.
- Saghaian S, Karaca H, Tobe H, Turabi A, Saedi S, et al. (2017) High strength NiTiHf shape memory alloys with tailorable properties. Acta Materialia 134: 211-220.
- Melchels FP, Bertoldi K, Gabbrielli R, Velders AH, Feijen J, et al. (2010) Mathematically defined tissue engineering scaffold architectures prepared by stereolithography. Biomaterials 31: 6909-6916. [Crossref]
- Rho JY, Ashman RB, Turner CH (1993) Young's modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements. J Biomech 26: 111-119. [Crossref]







