Studies show that millions of people throughout the world lose their lives as the result of sudden cardiac death (SCD) each year. These deaths can be reduced by using medical equipment such as defibrillators. However, there is still an urgent need for a suitable way to predict SCD so that the doctors can take proper decisions for patients at risk. In this paper, we investigated a way to predict sudden cardiac death. To do this, we first extract the HRV signal from ECG signal and elicit informative nonlinear and time-frequency features. Then, the dimension of feature space is reduced by applying feature selection and finally, healthy persons and those at risk of SCDs are classified using MLP and KNN neural networks. To evaluate the capabilities of analytical methods in classification, we have compared the classification rates by using both separate and combined nonlinear and TF features. The results show that there are features in the HRV signal of patients prone to SCD before the onset of SCD, which noticeably differ from those of normal people. Another remarkable result to emerge from our analysis is that the combination of time- frequency and nonlinear features have a better ability to detect this evident difference. The proposed method demonstrates that four minutes prior to the occurrence of SCD, the signals of a normal person and one of at risk can be differentiated in an effective and a reliable manner, which in turn, can make possible the provision of timely treatments.
sudden cardiac death, heart rate variability, time – frequency transform, linear processing, nonlinear processing, ECG signal
Sudden Cardiac Death (SCD), resulted from a precipitous loss of heart function, is a leading cause of cardiovascular mortality in modern socialites. This is a very serious cardiac event that will claim the patient’s life within few minutes [1,2]. When this occurs, no blood can be pumped to the rest of the body within minutes in a person with known or unknown cardiac disease.
Despite the significant decline in coronary artery disease (CAD) mortality in the second half of the 20th century, sudden cardiac death (SCD) continues to claim 250 000 to 300 000 US lives annually. In North America and Europe the annual incidence of SCD ranges between 50 to 100 per 100000 in the general population. Due to the lack of emergency medical response systems in most world regions, worldwide estimates are currently not available. However, even in the presence of advanced first responder systems for resuscitation of out-of-hospital cardiac arrest, the overall survival rate in a recent North American analysis was 4.6% [3]. Astonishingly, the victim may not even have been diagnosed with heart disease. Also, the time and mode of death is quite unexpected [4]. Most victims (>90%) have previously known or unrecognized cardiac abnormality [5-9]. These life-threatening arrhythmias that indicate SCD are most often initiated with a sustained ventricular tachyarrhythmia, including ventricular tachycardia (VT), ventricular flutter (VFL), or ventricular fibrillation (VFib). A smaller percentage of SCD events are related to a primary brady arrhythmia [10]. SCD may abruptly strike any person, young or elderly, if they are at high risk of heart disease. Besides utilizing public access defibrillation (PAD) procedure to recue impending death patient after the collapse, a more reliable solution is to prevent onset SCD by adopting medical aid prior to the occurrence of SCD. Thus, it should be made possible to make an early warning around half an hour before the crisis presents itself. [11].
Ichimaru et al. found that the respiratory peak of the heart rate variability (HRV) in SCD patient disappeared during the night time one week before death [12]. Van Hoogenhuyze, D., Martin, et al. observed two HRV measurements, standard deviation of mean of sinus R-R intervals (SDANN) and mean of SD (SD), from 24 hrs HRV. They have evidence to show that HRV is low in patients who experience SCD and is high in young healthy subjects [13]. In our early and encouraging experiments, we showed that the TF method can classify normal and SCD subjects, more efficiently than the classical method [14]. Moreover, we evaluated both TF and Classic methods through the MLP classifier for one-minute ECG signal before SCD by the accuracy of 99.16% and 74.36%, respectively. However, the relationship between short-term HRV and SCD is unknown. In addition, repolarization alter nans phenomenon provides a safe, noninvasive maker for the risk of SCD, and has proven equally effective to an invasive and more expensive procedure - invasive electrophysiological study (EPS), which is commonly used by cardiac electrophysiologists [15,16].
Analysis of heart rate variability (HRV) has provided a noninvasive method for assessing cardiac autonomic control [17]. HRV is accepted like a strong and independent predictor of mortality after an acute myocardial infarction [18], such that a reduced HRV is associated with a higher risk for severe ventricular arrhythmia and sudden cardiac death [19]. In this research, the heart rate variability (HRV) signal is used to study sudden cardiac death (SCD). The common linear features and time-frequency (TF) domain features have been used to predict the sudden cardiac death. It should be noted that different linear methods have so far been applied for analysis of HRV signal. Nevertheless, studies in the literature suggest that classic linear methods fail to predict SCD effectively and reliably [14,10]. Recently, it has been brought to attention that the non-linear processing methods can provide more information than linear methods and can be a good complement for them [20]. In this article, we aim to conduct classic linear, time-frequency and non-linear analysis on HRV signal of healthy persons and patients prone to SCD. Therefore, we use combinational feature vector and neural classifiers to separate healthy subjects and those at risk. Having extracted HRV signal from ECG signal, we elicited linear features and applied the Wigner Ville transform to obtain time-frequency features. Finally, nonlinear features are extracted. Subsequently, feature dimensionality is reduced through employing combinational feature vector and feature selection methods. In the next stage, Multilayer perceptron (MLP) neural network and K-Nearest Neighbor (KNN) neural network are used to classify healthy persons and those susceptible to SCD. This classification is performed in 4 steps. The separability of each one-minute interval (i.e., the first one minute, the second one minute, the third one minute and the forth one minute before SCD) in prediction of SCD is evaluated through calculating the accuracy. Figure 1 illustrates the block diagram of the proposed method.
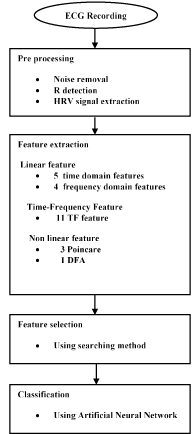
Figure 1. Flowchart of proposed algorithm.
The proposed method is evaluated on a database containing 35 patients with sudden cardiac death (including 16 females and 19 males, with a sampling rate of 256 Hz, aged 18 to 89, 12 observations have been obtained from other channels) and 35 normal people (including 5 males, aged 26 to 45, and 13 females, aged 20 to 50, with a sampling rate of 128 Hz, 17 observations have been obtained from other channels). This open access database is prepared by MIT-BIH database with the title of Sudden Cardiac Death Holter database & Normal Sinus Rhythm database.
In cases that for each observation (patient), two channels were available, each channel is used as a separate observation (patient).
Preprocessing of ECG signal
The dataset consists of 24-hour ECG recordings (Holter) before the event of heart death and several seconds after that. Patients who show signs of a previous heart attack or having the hard tachyarrhythmia are susceptible to SCD, and finally they succumb to SCD. One-minute time series segments prior to the onset of SCD are separated and named as the first minute, second minute, third minutes and fourth minutes, respectively. Figure 2 shows an electrocardiogram signal of a 34-year-old patient that has led to sudden cardiac death. Before the occurrence of SCD, there is no difference between the ECG signal of person susceptible to heart death and that of a normal person. Figure 3 depicts a sample of ECG signal of a person with SCD several seconds before the onset of SCD and a few seconds after.
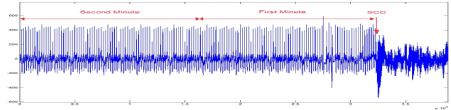
Figurge 2. The ECG signal of SCD patient, from 2 minute before SCD event and several seconds after that.
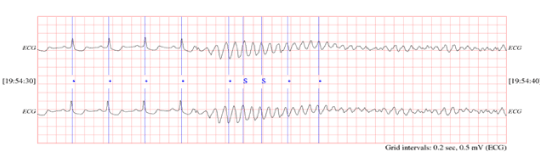
Figure 3. ECG signal of person on the moment of hearth death.
One minute before the occurrence of the sudden cardiac death was selected as ECG recordings for patients. For normal subjects one minute of the ECG signal was selected at random. Then, the Pan-Tompkins [21] algorithm was used to detect the QRS-complexes in the ECG-signal from which we could determine the RR-intervals and HRV signal. Thus, the preprocessed HRV signal is now ready to extract features from it. In the Figure 4 & Figure 5 show HRV and ECG signals of a healthy person and those of an SCD subject.
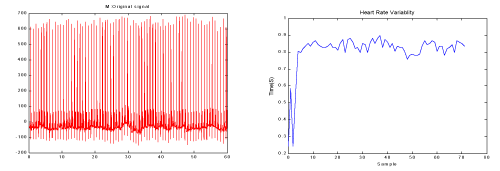
Figure 4. a) One minute of the ECG signal of a healthy person b) The HRV signal which was extracted from figure a.
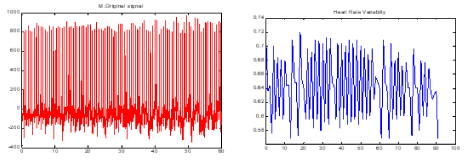
Figure 5. a) One minute the ECG signal of a patient just before occurrence of SCD. b) The HRV signal which was extracted from part a.
In this step, a number of common linear features are extracted. They include 5 features in the time domain and 4 features in the frequency domain.
Time-domain features
Statistical time-domain measures were divided into two classes:
- Direct measurements of NN intervals
- Measurements from the differences between NN intervals
Direct measurements of NN intervals: These features include two simple time domain variables that can be calculated by:
1. Mean of all NN intervals (MNN).
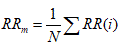
2. Standard deviation of all NN intervals (SDNN).
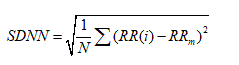
which reflects all the cyclic components responsible for variability in the period of recording
Measurements from the differences between NN intervals: The most commonly used measures derived from interval differences include:
1. The square root of the mean of the sum of the squares of differences between adjacent NN
Intervals ( RMSSD).
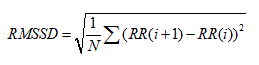
2. The standard deviation of differences between adjacent NN intervals (SDSD).
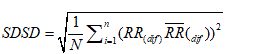
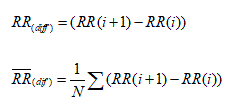
3. The proportion derived by dividing the number of interval differences of NN intervals greater than 50 ms by the total number of NN intervals (PNN50) [22].
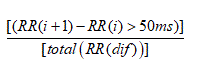
Frequency domain features
Although the time domain parameters are computationally effective, they lack the ability to discriminate between the sympathetic and parasympathetic contents of the RR intervals. It is generally accepted that the spectral power in the high frequency (HF) band (0.15-0.4 Hz) of the RR intervals reflects the respiratory sinus arrhythmia (RSA) and thus cardiac vagal activity. On the other hand, the low frequency (LF) band (0.04-0.15 Hz), is related to the baroreceptor control and is mediated by both vagal and sympathetic systems [23]. In this work, the LF, HF,VLF and ratio of the LF and HF bands power (LF/HF) is used as the frequency domain features of the RR interval signal [24].
The power spectral density(PSD), shown in Figure 6, was computed using Burg parametric method.
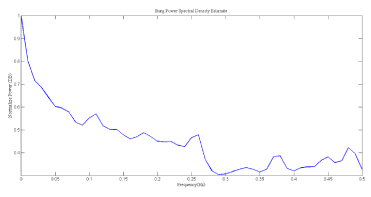
Figure 6. PSD of HRV signal, power in each frequency band was indicated.
Spatial scattering of two of these features is shown in Figure 7. As can be seen, these features are suitable for discriminating between the two groups, i.e. the healthy and SCD subjects.
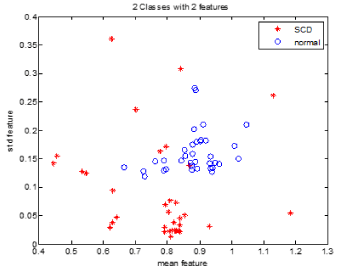
Figure 7. Spatial distribution of mean (in horizontal axis) and std (in vertical axis)..
An approach to analyzing non stationary HRV signal is applying time-frequency (TF) methods which can be divided into three main categories: nonparametric linear TF methods based on linear filtering, including the short-time Fourier transform [25,26] and the wavelet transform [27,28], nonparametric quadratic TF representations, including the Wigner- Ville distribution and its filtered versions [29-32], and parametric time-varying methods based on autoregressive models with time-varying coefficients [33,34]. In this paper the Smoothed Pseudo Wigner-Ville distribution (SPWVD) is preferred since it provides better time frequency resolution than nonparametric linear methods, an independent control of time and frequency filtering, and power estimates with lower variance than parametric methods when rapid changes occur [30]. The main drawback of the SPWVD is the presence of cross-terms, which should be suppressed by the time and frequency filtering. The SPWVD of the discrete signal x(n) is defined by [31].
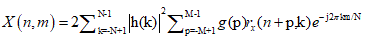
where n and m are the discrete time and frequency indexes, respectively, h(k) is the frequency smoothing symmetric normed window of length 2N−1 , g(p) is the time smoothing symmetric normed window of length 2M − 1 and rx(n, k) is the instantaneous autocorrelation function, defined as
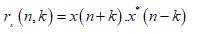
Figure.8 shows the result of applying Wigner Ville transform to the HRV signal.
Figure 8. Wigner Ville transform of the HRV signal of a SCD person.
TF features extraction
Each HRV signal is divided into 5 segments of equal length, each segment is approximately 15 seconds in time domain. The average energy of each segment was computed. The features are:
MAX w: maximum amount of energy in each window.
MIN w: minimum amount of energy in each window.
DIF w: difference between maximum and minimum amount of energy between windows.
STD w: standard deviation between energy of time windows.
The obtained signal in TF domain is also divided into three frequency segments.
Evlf : the complex of energy signal in very low frequency band(0.003-0.04) Hz, divided by length of band(0.037)
Elf : the complex of energy signal in low frequency band(0.04-0.15) Hz, divided by length of band(0.11)
Ehf : the complex of energy signal on high frequency band(0.15-0.4) Hz, divided by length of band(0.25).
Fvlf : the average of energy signal in very low frequency band (0.04-0.003)Hz.
Flf : the average of energy signal in low frequency band(0.04-0.15)Hz.
Fhf : the average of energy signal in high frequency band(0.15-0.4)Hz.
Also, we have defined the first order derivative as a feature to show the difference between adjacent windows. This derivative is the difference between the average energy in subsequent windows. This derivative for the first window (first 15 S) was computed by the difference between this window and the last 15 seconds in the second minute. So the first order derivative feature is computed as below
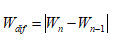
The result of features survey in time span of 15 seconds illustrates that in an SCD person, the features changes from one window to next window is much more prominent so we define the first order derivative.
Without a doubt, the cardiovascular system is more complex than linear systems and also has non-stationary behaviors. There are two non-linear analyses that illustrate chaotic dynamical characteristics in HRV signal and are used for classifying healthy persons and patients prone to SCD. Two different nonlinear parameters of the RR intervals are used in this work, which are described as below.
Poincare plot
When in the RR intervals, each interval RR (n +1) is plotted as a function of previous interval RR(n) , the resulting plot is known as the Poincaré plot, which is a relatively new tool for RR interval signal analysis. Poincaré plot can be seen as a graphical representation of the correlation between the successive RR intervals. This plot can be quantitatively analyzed by calculating the standard deviations of the distances of the points RR(i) from the lines y = x and y = -x +2RRm, where RRm is the mean of all RR(i) values. These standard deviations are denoted by SD1 and SD2, respectively. In fact, SD 1represents the fast beat-to-beat variability, while SD2 describes the relatively long-term variability in the HRV signal [35]. The length (SD2) and the width (SD1) of the long and short axes of Poincaré plot images represent short and long-term variability of any nonlinear dynamic system [36]. We developed mathematical formulations that relate each measure derived from Poincaré plot geometry to well understood existing heart rate variability indexes (see Fig. 9 & Fig. 10)[36]. A strong correlation was found when comparing high frequency power of heart rate signals (modulated by parasympathetic nervous system) to SD1 [37]. SD2 was found to be well correlated with both low and high frequency power (modulated by both the parasympathetic and sympathetic nervous system) [37]. The ratio SD1/ SD2 is usually used to describe the relation between the two components [22,38,39].
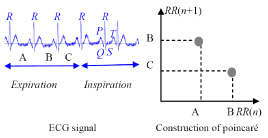
Figure 9. Encoding HRV data using Poincaré plot.
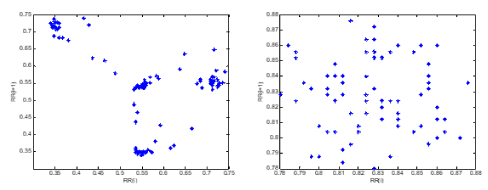
Figure 10. a) the Poincare plot of an SCD subject and b) Poincare plot of a normal subject.
Analysis method DFA
Detrended fluctuation analysis (DFA) is a method for quantifying long-range correlations embedded in a seemingly non-stationary time series, and also avoids the spurious detection of apparent long-range correlations that are an artifact of non-stationarity. This method is a modified root mean square analysis of a random walk [22,40-45].
To discriminate between ECG of normal person and a person who is prone to sudden cardiac death, The Multilayer perceptron (MLP) neural network and K-Nearest Neighbor (KNN) neural network classifier have been used. Features extracted from HRVs of one-minute intervals (i.e., the first one minute, the second one minute, the third one minute and the fourth one minute before SCD) were compared to normal HRVs of one minute.
Multilayer perceptron
MLP network formed in three layers using error back propagation algorithm with variable learning rate [46-52]. By changing the number of hidden layer neurons, we have tried to optimize the neural network architecture. The best selection was a three-layer neural network consisting of an input layer, a hidden layer and an output layer. The input layer has a number of nodes equal to the input vector length (7 node). The output layer consists of one node, accounting for a possibility of only 2 classes to be classified. Also, the number of nodes in the hidden layer is 5. Both input and output nodes use linear transfer functions, and the hidden layer uses a sigmoid function.
k-Nearest neighbor
k-Nearest neighbor (k-NN) algorithm is one of the most effective non-parametric methods in pattern recognition [53]. The k-NN algorithm is a method for classifying objects based on their distance to the training examples in the feature space. The k-NN algorithm is among the simplest of all machine learning algorithms. The algorithm is independent from statistical distribution of training examples. There are several distance measures that might be used in this algorithm. However Euclidean distance is commonly preferred as the distance measure. An object is classified by the majority vote of its neighbors, and the object is assigned to the class most common among its k nearest neighbors. The number k is usually chosen small. If k = 1, then the object is simply assigned to the class of its nearest neighbor. The selected feature set is then used to determine the best value of k for the classifier. Therefore, different numbers of nearest neighbors (k = 1, 3, 5, 7, 9, 11, 13) are tested in the k-NN classifier to obtain the best performance for the classifier [54-57]. Performances of all classifiers are calculated based on their accuracy. the maximum performance is provided by a 7-nearest neighbor classifier. Network training continued until the mean square error became less than 0.01 or the number of training iterations reached to 1000. Due to the limited input data set, Leave One Out cross-validation method was done for training [45]. At each stage one of observations was selected as test data and 69 as train data, and this process repeated 70 times. Another, words for each experiment use 69 examples for training and the remaining example for testing. Network error in each step was computed, and finally the average was calculated. One advantage of this approach is that all the input data set are present in both processes (train and test) As asynchronous and the network shows it is all capabilities. The same process was done for KNN classifier.
In this stage, firstly for evaluating the separability of features, the extracted features are compared with each other in both individual (linear, nonlinear and time-frequency) and optimal combinational modes. The separability of linear, non-linear and time-frequency features and also combinational mode is calculated three minutes (180s) and two minutes(120s) before SCD and is shown in Table 1.
Table 1. Average of separating percentage between healthy persons and patients prone to SCD 4 minutes before the onset of SCD using combinational vector motion method
Average Classification Rate with combinational feature vector |
|
Two-Minutes (120 S before SCD) |
Three-Minutes (180 S before SCD) |
Features |
MLP |
KNN |
MLP
KNN |
Linear |
71.08% |
69.57% |
68.82% |
68.13% |
Time-Frequency |
80.16% |
77.13% |
76.41% |
74.96% |
Non- Linear |
85.38% |
84.33% |
82.17% |
83.58% |
Combinational |
98.74% |
96.42% |
95.78% |
93.63% |
Wang and et al [10] used 2-minute (just before SCD) of the same dataset to predict SCD. Table 2 shows the results of our method and Wang's method. As it can be seen, the predictive accuracy has been improved from 67.44% to 91.23%.
Table 2. Predictive accuracy for the proposed method and Wang's method [10] (2-minute analysis)
|
Comparison Methods
|
Ref [10]
|
Our Methods
|
MLP
|
67.44%
|
98.74%
|
As can be seen in Table 1, combinational features have more capability in classification of people (i.e., Normal and SCD). That is why combinational features have been used in this study as input feature vector to predict SCD. In this way, HRV signals (before SCD) have been partitioned into one minute intervals. Then, the separability of each one-minute interval (i.e., the first one minute, the second one minute, the third one minute and the forth one minute before SCD) in prediction of SCD is evaluated through the computing accuracy. The obtained results show that the combinational feature vector can predict SCD by the accuracy of 99.73%, 96.52%, 90.37% and 83.96 for the first, second, third and fourth one minute intervals, respectively. The results also denote that the two minutes’ interval before SCD contains more information related to the SCD which can be used for prediction. In other words, the first one-minute interval before SCD contains more valuable information for prediction of SCD in comparison with other intervals (i.e., the second, third and fourth intervals), which is expectable from the medical perspective. Also, the ability of combinational feature vector in predicting of SCD is evaluated through the KNN classifier by the accuracy of 81.49%, 88.93%, 95.04%, and 98.32%. Table 3 shows the percentage of separating 4 minutes before the onset.
Table 3. Average of separating percent between healthy person and patients prone to SCD, 4minute before incident by means of composition vector motion method
Average classification rate with composition feature vector |
2021 Copyright OAT. All rights reserv
Classifier |
Forth one minute |
Third one minute |
Second one minute |
First one minute |
MLP |
83.96% |
90.37% |
96.52% |
99.73% |
KNN |
81.49% |
88.93% |
95.04% |
98.32% |
As it is seen, although there is not a significant difference between ECG of a normal person and that of a patient prone to SCD, by using the proposed combinational feature vector, symptoms of SCD can be observed even 4 minutes before SCD. In other words, in spite of that cardiology & electrocardiography experts cannot distinguish between normal ECG and patients who are prone to SCD, the proposed extracted features can be used to predict SCD. It is highlighted that those intervals which are closer to SCD have more capability for prediction of SCD.
Experimental results show there are significant information in HRV signal which can be extracted through the proposed method and be used for prediction of SCD although there is no difference between normal ECG and those ones which prone to SCD. This study has proposed a new combinational feature vector which contains more valuable information for prediction of SCD in comparison with previous works. The results of this research illustrates that in the electrocardiogram signal of a SCD patient, there are features that are majorly different from healthy person’s features. These differences could not be detected by classic methods, in contrast, the time-frequency (TF) methods are shown to be effective in serving the purpose.
Simply put, we have shown that the 2 minutes interval before SCD can be used to distinguish between a person who is prone to SCD and a normal ECG. Also, the third minute interval before SCD carries information presenting high risk of SCD that can be estimated through the proposed method. Moreover, by closing to the SCD, the risk of SCD increases which is expectable from the medical perspective. In the fourth one minute before the onset of SCD, the risk of SCD exists although it has been decreased in comparison with the previous intervals which are closer to the SCD. Generally, healthy and unhealthy persons can be classified by detecting heart attack and tachyarrhythmia before SCD, because patients who show signs of a previous heart attack or having the hard tachyarrhythmia are susceptible to SCD, and may finally succumb to SCD. In this study, we have introduced a new approach which uses a combinational feature vector to predict SCD. It is noticeable that, when approaching the onset of SCD from the fourth interval, the percentage of correct detection of SCD rises dramatically and then climbs sharply for the closest interval to the SCD. Moreover, it is demonstrated that MLP classifier has better performance in detection of SCD than KNN classifier. Finally, our findings about detection of SCD can warn doctors of an imminent SCD 4 minutes before the event, helping them provide timely treatments that save the patient’s life.
- Lin J (2002) A few evidence in patient’s ECG shown high risk existed inducing syncope or SCD. J Electrocardiology 21: 95-198.
- Chen X (2000) The patient with high risk of sudden cardiac death. The Chinese Journal of Arrhythmia 4: 307-308.
- Fishman GI, Chugh SS, Dimarco JP, Albert CM, Anderson ME, et al. (2010) Sudden cardiac death prediction and prevention: report from a National Heart, Lung, and Blood Institute and Heart Rhythm Society Workshop. Circulation 122: 2335-2348. [Crossref]
- Jones JL, Tovar OH (1996) The mechanism of defibrillation and cardioversion. Proceedings of the IEEE 84: 392-403.
- Wever EF, Hauer RN, Oomen A, Peters RH, Bakker PF, et al. (1993) Unfavorable outcome in patients with primary electrical disease who survived an episode of ventricular fibrillation. Circulation 88: 1021-1029. [Crossref]
- Zipes DP, Wellens HJ (1998) Sudden cardiac death. Circulation 98: 2334-2351. [Crossref]
- [No authors listed] (1997) Survivors of out-of-hospital cardiac arrest with apparently normal heart. Need for definition and standardized clinical evaluation. Consensus Statement of the Joint Steering Committees of the Unexplained Cardiac Arrest Registry of Europe and of the Idiopathic Ventricular Fibrillation Registry of the United States. Circulation 95: 265-272. [Crossref]
- Chugh SS, Kelly KL, Titus JL (2000) Sudden cardiac death with apparently normal heart. Circulation 102: 649-654.
- Chugh SS (2001) Sudden cardiac death with apparently normal heart: clinical implications of progress in pathophysiology. Cardic Electrophysiology Review 5: 394-402.
- Shen TW, Shen HP, Lin CH, Ou YL (2007) Detection and prediction of sudden cardiac death (SCD) for personal healthcare. Conf Proc IEEE Eng Med Biol Soc 2007: 2575-2578. [Crossref]
- Fang Z, Lai D, Ge X, Wu X (2009) Successive ECG telemetry monitoring for preventing sudden cardiac death. Conf Proc IEEE Eng Med Biol Soc 2009: 1738-1741. [Crossref]
- Fang Z, Lai D, Ge X, Wu X (2009) Successive ECG telemetry monitoring for preventing sudden cardiac death. Conf Proc IEEE Eng Med Biol Soc 2009: 1738-1741. [Crossref]
- Ichimaru Y (1988) Circadian changes of heart rate variability. Proceedings of Computers in Cardiology 315-318.
- VanHoogenhuyze D (1989) Spectrum of heart rate variability. Proceedings of Computers in Cardiology 65.
- Ebrahimzadeh E, Pooyan M (2011) Early detection of sudden cardiac death by using classical linear techniques and time-frequency methods on electrocardiogram signals. Biomedical Science and Engineering 11: 699-706.
- Mrowka R, Theres H (1998) Alternans-like phenomena due to filtering of electrocardiographic data. Proceedings of Computers in Cardiology 725-727.
- Meeting Report (2006) Non-invasive test to predict sudden cardiac death proven effective. American Heart Association (AHA).
- Acharya R, Kumar A, Bhat PS, Lim CM, Iyengar SS, et al. (2004) Classification of cardiac abnormalities using heart rate signals. Med Biol Eng Comput 42: 288-293. [Crossref]
- Task Force of the Europe Society of Cardiology and the North American Society of Pacing and Electrophysiology (1996) Heart rate variability-standards of measurement, physiological interpretation and clinical use. Circulation 93: 1043-1065.
- Kurths J, Voss A, Saparin P, Witt A, Kleiner HJ, et al. (1995) Quantitative analysis of heart rate variability. Chaos 5: 88-94. [Crossref]
- Joo S, Choi KJ, Huh SJ (2012) Prediction of spontaneous ventricular tachyarrhythmia by an artificial neural network using parameters gleaned from short-term heart rate variability. Expert Systems with Applications 39: 3862-3866.
- Pan J, Tompkins WJ (1985) A real-time QRS detection algorithm. IEEE Trans Biomed Eng 32: 230-236. [Crossref]
- Obayya M, Chadi FA (2008) Data fusion for heart diseases classification using multi-layer feed forward neural network. IEEE 67-70.
- Task force of the European society of cardiology and the North American society of pacing and electrophysiology (1996) Heart rate variability – standards of measurements, physiological interpretation, and clinical use. Eur Hear J 17: 354-381.
- Mohebbi M, Ghassemian H (2008) Detection of atrial fibrillation episodes using SVM. Conf Proc IEEE Eng Med Biol Soc 2008: 177-180. [Crossref]
- Martinmäki K, Rusko H, Saalasti S, Kettunen J (2006) Ability of short-time Fourier transform method to detect transient changes in vagal effects on hearts: a pharmacological blocking study. Am J Physiol Heart Circ Physiol 290: H2582-2589. [Crossref]
- Keselbrener L, Akselrod S (1996) Selective discrete Fourier transform algorithm for time-frequency analysis: method and application on simulated and cardiovascular signals. IEEE Trans Biomed Eng 43: 789-802. [Crossref]
- Toledo E, Gurevitz O, Hod H, Eldar M, Akselrod S (2003) Wavelet analysis of instantaneous heart rate: a study of autonomic control during thrombolysis. Am J Physiol Regul Integr Comp Physiol 284: R1079-1091. [Crossref]
- ClariA F, Vallverdd M, Baranowski R, Chonowska L, Martinez P, et al. (2000) Time-frequency representation of the HRV: A tool to characterize sudden cardiac death in hypertrophy cardiomyopathy patients. IEEE 71-73.
- Novak P, Novak V (1993) Time/frequency mapping of the heart rate, blood pressure and respiratory signals. Med Biol Eng Comput 31: 103-110. [Crossref]
- Pola S, Macerata A, Emdin M, Marchesi C. Estimation of the power spectral density in non-stationary cardiovascular time series: assessing the role of the time-frequency representations (TFR). IEEE.
- Pola S, Macerata A, Emdin M, Marchesi C (1996) Estimation of the power spectral density in nonstationary cardiovascular time series: Assessing the role of the time-frequency representations (TFR). IEEE Trans Biomed Eng 43: 46-59. [Crossref]
- Mainardi LT, Montano N, Cerutti S (2004) Automatic decomposition of Wigner distribution and its application to heart rate variability. Methods Inf Med 43: 17-21. [Crossref]
- Jasson S, Médigue C, Maison-Blanche P, Montano N, Meyer L, et al. (1997) Instant power spectrum analysis of heart rate variability during orthostatic tilt using a time-/frequency-domain method. Circulation 96: 3521-3526. [Crossref]
- Bianchi AM, Mainardi LT, Meloni C, Chierchia S, Cerutti S (1997) Continuous monitoring of the sympatho-vagal balance through spectral analysis. Recursive autoregressive techniques for tracking transient events in heart rate signals. IEEE Eng Med Biol Mag 16: 64-73.
- Farina D, Lucas MF, Doncarli C (2008) Optimized wavelets for blind separation of nonstationary surface myoelectric signals. IEEE Trans Biomed Eng 55: 78-86. [Crossref]
- Tulppo MP, Mäkikallio TH, Takala TE, Seppänen T, Huikuri HV (1996) Quantitative beat-to-beat analysis of heart rate dynamics during exercise. Am J Physiol 271: H244-252. [Crossref]
- Brennan M, Palaniswami M, Kamen P (2001) Do existing measures of Poincaré plot geometry reflect nonlinear features of heart rate variability? IEEE Trans Biomed Eng 48: 1342-1347. [Crossref]
- Brennan M, Palaniswami M, Kamen P (2002) Poincaré plot interpretation using a physiological model of HRV based on a network of oscillators. Am J Physiol Heart Circ Physiol 283: H1873-1886. [Crossref]
- Mohebbi M, Ghassemian H (2008) Detection of atrial fibrillation episodes using SVM. Conf Proc IEEE Eng Med Biol Soc 2008: 177-180. [Crossref]
- Azuaje F, Dubitzky W, Wu X, Lopes P, Black ND, et al. (1997) A neural network approach to coronary heart disease risk assessment based on short-term measurement of RR intervals. Computers in Cardiology 1997: 53-56.
- Peng CK, Havlin S, Stanley HE, Goldberger AL (1995) Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 5: 82-87. [Crossref]
- Iyengar N, Peng CK, Morin R (1996) Age-related alterations in the fractal scaling of cardiac interbeat interval dynamics. Am J Physiol 271: R1078.
- Mäkikallio TH, Huikuri HV, Mäkikallio A, Sourander LB, Mitrani RD, et al. (2001) Prediction of sudden cardiac death by fractal analysis of heart rate variability in elderly subjects. J Am Coll Cardiol 37: 1395-1402. [Crossref]
- Huikuri HV, Mäkikallio TH, Peng CK, Goldberger AL, Hintze U, et al. (2000) Fractal correlation properties of R-R interval cynamics and mortality in patients with depressed left ventricular function after an acute myocardial infraction. Circulation 101: 47-53. [Crossref]
- Yeh R, Shieh J, Han Y, Wang Y, Tseng S (2006) Detrended fluctuation analyses of short-term heart rate variability in surgical intensive care units. Biomedical Engineering Applications, Basis & Communications 18.
- Vapnik VN (1998) Statistical Learning Theory. John Wiley & Sons, Inc., New York.
- Nikravan M, Ebrahimzadeh E, Izadi MR, Mikaeili M (2016) Toward a computer aided diagnosis system for lumbar disc herniation disease based on MR images analysis. Biomedical Engineering: Applications, Basis and Communications 28: 1650042.
- Ebrahimzadeh E, Pooyan M, Jahani S, Bijar A, Setaredan SK (2015) ECG Signals noise removal: Selection and optimization of the best adaptive filtering algorithm based on various algorithms comparison. Biomedical Engineering: Applications, Basis and Communications 27: 1550038.
- Ebrahimzadeh E, Alavi SM, Bijar A, Pakkhesal A (2013) A novel approach for detection of deception using Smoothed Pseudo Wigner-Ville Distribution (SPWVD). Journal of Biomedical Science and Engineering 6: 8.
- Ebrahimzadeh E, Manuchehri MS, Amoozegar S, Araabi BN, Soltanian-Zadeh H (2017) A time local subset feature selection for prediction of sudden cardiac death from ECG signal. Medical & biological engineering & computing 1-18.
- Ebrahimzadeh E, Pooyan M (2011) Early detection of sudden cardiac death by using classical linear techniques and time-frequency methods on electrocardiogram signals. Journal of Biomedical Science and Engineering 4: 699.
- Ebrahimzadeh E, Pooyan M1, Bijar A (2014) A novel approach to predict sudden cardiac death (SCD) using nonlinear and time-frequency analyses from HRV signals. PLoS One 9: e81896. [Crossref]
- Cover TM, Hart PE (1968) Nearest neighbor pattern classification. IEEE Trans Inform Theory 21-27.
- Kutlu Y, Kuntalp D (2012) Feature extraction for ECG heartbeats using higher order statistics of WPD coefficients. Comput Methods Programs Biomed 105: 257-267. [Crossref]
- Ebrahimzadeh E, Araabi BN (2016) A Novel approach to predict sudden cardiac death using local feature selection and mixture of experts computational intelligence in electrical engineering 7: 15-32.
- Amoozegar S, Pooyan M, Ebrahimzadeh E (2013) Classification of brain signals in normal subjects and patients with epilepsy using mixture of experts.
- Ebrahimzadeh E, Alavi SM, Samsami Khodadad F (2013) Implementation and designing of lie-detection system basedon electroencephalography (EEG). Sci Res J Army Univ Med Sci I.R. Iran 11: 20.










