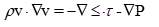Take a look at the Recent articles

Abstract

Background and Objective: The mutual contribution of each of these in LM bifurcation has not been yet evaluated in a computational model. To investigate the impact and the relationships among bifurcation angles and different left main (LM) stenting techniques using computational fluid dynamic (CFD) analysis.

Methods: We reconstructed a LM bifurcation after analyzing 50 consecutive patients (mean age 77.4 ± 4.3, 39 males) with LM distal/bifurcation disease. Consequently, LM bifurcation angles to test were set to:  45°, 60° and 85°. A 90% lesion was added to each vessel obtaining a Medina 1.1.1 LM bifurcation disease.  Techniques for LM bifurcation stenting included Nano-crush, DK-crush and Culotte. 

Results: The Nano-crush obtained the higher averaged WSS in MB and SB at any angle compared to the other two techniques. At the carina the WSS are slightly lower at 45° and highest at 60° and 80° degrees. The DK crush resulted to show the higher values of WSS at the carina at any angles while it achieved the largest lower WSS at MB and SB in particular at 60° degrees. Finally, the Culotte obtained the lower averaged WSS in particular at the carina and SB at 60° degrees and slightly worse compared to the other two techniques at 45° and 80° degrees.

Conclusions: The study confirmed the role of angles in LM bifurcation rheology and enhanced the impact of bifurcation angles on double stenting techniques in terms of WSS.

Key words

Coronary artery disease, Percutaneous coronary intervention, Mathematic Computing

Introduction

In human coronary bifurcation, angles and stenting technique have been suggested to impact coronary vessel physiology both before and after stenting. Specifically, before stenting, wide angles have been suggested to induce low wall shear stress (WSS) gradient [1-2], whereas specific stent techniques used in bifurcation stenting have been recently reported to impact on bifurcation rheology [3] and on the level of shear stress at the carina and side branch (SB) in particular after double stenting technique.

Nowadays, distal and bifurcation left main (LM) percutaneous interventions are gaining robust scientific evidences [4,5] and cross-over stenting is considered a relatively safe alternative to bypass grafting in case of simple LM distal or bifurcation disease [6]. Double stenting techniques, although highly debated, are considered useful in complex LM disease with contraindications to bypass grafting. Unfortunately, double stenting techniques are graved by some uncertainties due to the amount of stent thrombosis and target vessel revascularization (TVR) compared to cross-over stenting. The mechanisms of these differences are not yet clearly understood [6]. The mutual contributions of bifurcation angle and specific techniques in LM bifurcation interventions has not been yet evaluated. These data would be of value in order both to understand the mechanisms of increased failure of double stenting in LM and eventually to plan future strategies.

The aim of our study is to investigate by means of computation fluid dynamic analysis (CFD) the impact of bifurcation angles and specific bifurcation stenting techniques on left main coronary artery rheology.

Methods

The virtual simulations included three bifurcation angles and three different double stenting techniques including the Nano-crush, the DK-Crush and the Culotte.

Construction of the virtual model

For the computational domain analysis, we reconstructed a LM bifurcation after analysing 50 consecutive patients (mean age 77.4 ± 4.3, 39 males) with LM distal/bifurcation disease who underwent percutaneous coronary intervention (PCI) between the 1st January 2015 and the 1stJanuary 2017. The mean diameter of proximal LM, left anterior descending (LAD) and left circumflex (LCX), evaluated with quantitative coronary analysis (QCA)were 4.32 ±0.82 mm, 3.21±0.65 mm, and 2.52±0.88 mm, respectively. Following these measurements diameters of LCA and LCX were modelled as following: LM 4.5 mm, LAD 3.5 mm, LCX 2.75 mm. The mean LAD-LCX bifurcation angle, measured after the diagnostic angiography using an electronic goniometer was divided in tertiles (α° = 43.2±2.2, α° = 58.8±3.1, α° = 82.3±3.8) and divided for the purpose of the analysis in three models: Model 1) α° 45°, Model 2) α° 60°, Model 3) α° 85 °.  A 90% stenosis lesion in the distal LM and proximal LAD and LCx was added to obtain a Medina 1.1.1 LM bifurcation disease (Figure 1). The hemodynamic conditions adopted into the model are assumed for a stable diastolic blood pressure of 80 mmHg (equal to about 10665 Pascal). The model was segmented using Osirix (Ver 6.5.1) and then constructed using Rhinoceros v. 4.0 Evaluation (McNeel & Associates, Indianapolis, IN).

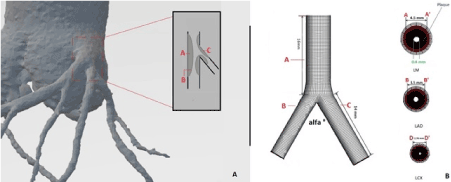
Figure 1. Left Coronary stem model: (A)Left Main (LM) , Left Circumflex (LCx) and  left anterior descending (LAD) coronary artery  were segmented, reconstructed and  modelled on the analysis of our patient’s dataset. A 90 % stenosis inducing plaques at distal LM and ostial LAD and LCx were added to obtain a Medina 1,1,1 LM bifurcation disease(B) Relative vessels diameters and lengths of the LM stem components.

Stent geometry reconstruction

For stent simulation, we reconstructed an idealized stent with strut design and linkage pattern of a third-generation, drug-eluting stent, with the same design of a Xience (Abbott Vascular, Santa Clara, CA, USA) and strut thickness set at 80 μm.  Computer Aided Design (CAD) software was used to reproduce the stented geometry as accurately as possible (SolidWorks 2009, Solidworks Corp, Concord, MA). In the first step, we created the solid model of the coronary artery bifurcation and then the expanded stent geometry. For this purpose, a hollow tube with outer diameter equal with both the nominal expanded diameter and thickness of the stent was created. Then, a 2-dimensional sketch with the stent's strut was propagated and wrapped around the tube. Through a cut out, the obtained ring of the stent was propagated axially to create the full-length expanded model.

Virtual implantation

After placing the stent model in the correct position, the stenting procedure was performed following the real procedural steps the three assessed techniques: Nano-crush, DK-crush and Culotte (Figure 2). Using Boolean operation, the modified solid model was subtracted from the bifurcation model to obtain the final geometry and more clearly show the WSS on the vessel wall. We assumed that after stent deployment and implantation there was no residual stenosis.

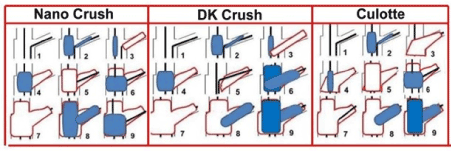
Figure 2. Schematic representation of the three double stenting techniques and relative steps which have been included into the virtual implantation procedure evaluated in the computational fluid dynamic analysis.

Nano-crush steps included: 1)Wiring both branches; 2)Predilation  of both branches with semi-compliant balloon 1:1  ratio with branches size; 3)SB stent deployment at nominal pressure with protrusion 1 ring in the LM, 4.0 mm non-compliant balloon parked into the LAD; 4) Withdrawal of the stent balloon and dilatation of the non-compliant 4.0 balloon  at 20 atm crushing the SB stent protruding  ring; 5)LM stent implantation with diameter equal to the proximal LAD at 18 atm; 6)POT with a 4.5 non-compliant balloon at 20 atm.; 7) rewiring SB; 8)Snuggle kissing balloon with 4.0 mm and 3.5 mm balloon at 20 atm; 9)Final POT with 4.5 balloon at 20 atm. DK Crush steps included: 1) Wiring both branches; 2)Predilation  of both branches with semi-compliant balloon 1:1ratio with branches size; 3)SB stent deployment at nominal pressure with generous protrusion in the LM and 4)crushing with dilation of 4.0 mm non-compliant balloon; 5)First Kissing balloon with 4.0 mm and 3.5 mm balloon at 20 atm with ; 6)Implantation of the LM stent at nominal pressure,7) rewiring SB; 8) opening of the LM stent strut with a small 2.0 semi compliant balloon at nominal pressure; 9)Final Kissing balloon  with 4.0 and 3.5  balloons.

The Culotte technique steps included: : 1)Wiring both branches; 2) Predilation  of both branches with semi-compliant balloon 1:1ratio with branches size; 3)SB stent deployment at nominal pressure with diameter equal to the proximal LCx; 4) rewiring of the LAD and opening of the  struts with dilatation of a semi compliant 4small balloon; 5)LM stent implantation with diameter equal to the proximal LAD at 18 atm; 6)POT with a 4.5 non-compliant balloon at 20 atm; 7)Rewiring of SB; 8)Opening of the SB strut by  a small semi-compliant balloon dilation;  9)Kissing balloon with 4.0 mm and 3.5 mm .

Computational fluid dynamic analysis

Blood was modelled as a non-Newtonian, viscous and incompressible fluid. Density was defined as 1060 kg/m³, according to the standard values cited in the literature [7-10]. Blood was represented by the Navier–Stokes equation

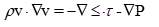
 and continuity equation

where v is the 3D velocity vector, P pressure, r density and τ the shear stress term. Instead, the Carreau model was applied for the viscosity of blood. Considering that coronary perfusion is mainly diastolic, we performed a steady flow simulation using a basal diastolic pressure of 80 mmHg (10665 Pa). In the analysis, the wall shear stress (WSS) (Pa) was evaluated at the lesion site and ostium whereas. More precisely, WSS has been defined as the force which is tangentially acting to the surface due to friction. As well known, low WSS are related to the development of greater plaque, higher neo-endothelization and necrotic core progression with a constrictive remodeling whereas high WSS segment develop greater necrotic core and calcium progression with expansive remodeling [11]. The numeric grid was obtained by the ANSYS Meshing 14.0 (Ansys, Inc., Canonsburg, PA) while the simulations were conducted using the commercial software ANSYS FLUENT 14.0 (Ansys, Inc., Canonsburg, PA).

Statistical analysis

Continuous variables were expressed as mean and standard deviation (SD) and groups have been compared using the ANOVA analysis. The differences were evaluated as delta between the mean WSS values at the same levels in the two models. All statistical analyses were carried out using SPSS statistical software version 19.0 (SPSS Inc, Chicago, IL, USA). A p value < 0.05 was considered statistically significant.

Results

Non-stented bifurcation

The analysis in the physiological model confirmed that the averaged WSS at the carina increased as the angle widens. Similarly, also the lower WSS area increased significantly as degree of the angle increased (Table 1). In both main and side branch, the WSS tended to be equal to those obtained at the carina. The WSS value significantly increased in both main and side branch when the angle passed from 45° to 60° and 85°.

Table 1. Computed fluid dynamic measurements of the considered parameters throughout the three angles considered . Baseline refers to the model before stent implantation.

	Model 1 α° = 43.2±2.2	Model 2 α° = 58.8±3.1	Model 3 α° = 82.3±3.8	p
Physiological model
Averaged WSS at the carina (Pa)	0.25±0.4	0.46±0.3	0.66±0.8	0.02
Area of lower WSS at the carina (mm2)	2.1±0.4	3.8±0.4	4.5±0.5	0.01
Averaged WSS MB (Pa)	0.25±0.3	0.45±0.2	0.65±0.6	0.03
Averaged WSS SB (Pa)	0.25±0.4	0.45±0.4	0.66±0.3	0.01
Pathological model MEDINA 1,1,1
Averaged WSS at the carina (Pa)	2.78±0.5	3.22±0.5	3.89±0.6	0.001
Area of lower WSS at the carina (Pa)	0.15±0.2	0.22±0.5	0.42±0.3	0.01
Averaged WSS MB (Pa)	1.52±0.4	1.92±0.6	2.54±0.5	0.01
Averaged WSS SB (Pa)	2.66±0.4	3.04±0.4	3.22±0.3	0.03

Stented bifurcation

The Nano-crush obtained a higher averaged WSS value in both the MB and SB at any angles compared to the other two techniques. At the carina the WSS was slightly lower at 45° and higher at 60° and 85° degrees than that of the DK and culotte technique, respectively. The DK crush resulted in higher values of WSS at the carina at any angles while the largest lower WSS area at MB and SB was achieved in particular at 60° degrees. Finally, the Culotte technique obtained high averaged WSS in particular at the carina and SB at 60° degrees with slightly worse values compared to the other two techniques at 45° and 80° degrees (Table 2, Figure 3 and 4).

Table 2. Computed fluid dynamic measurements of the considered parameters throughout the three angles considered after the three double stenting techniques evaluated.

	Model 1 α° = 43.2±2.2	Model 2 α° = 58.8±3.1	Model 3 α° = 82.3.±3.8	p
Averaged WSS carina (Pa)
Nano Crush	0.23±0.3	0.42±0.4	0.68±0.4	0.02
DK Crush	0.27±.0.3	0.47±0.2	0.67±0.5	0.01
Culotte	0.26±0.4	0.49±0.3	0.70±0.8	0.01
Area of lower WSS at the carina (mm2)
Nano Crush	2.3±0.4	3.9±0.6	4.9±0.2	0.02
DK Crush	2.2±0.7	3.6±0.3	4.7±0.2	0.03
Culotte	2.4±0.2	3.9±0.8	4.6±0.2	0.01
Averaged WSS MB (Pa)
Nano Crush	0.26±0.3	0.47±0.3	0.70±0.2	0.01
DK Crush	0.28±.0.4	0.46±0.2	0.68±03	0.02
Culotte	0.29±0.4	0.49±0.6	0.66±0.5	0.02
Averaged WSS SB (Pa)
Nano Crush	0.24±0.3	0.43±0.4	0.69±0.2	0.01
DK Crush	0.26±0.4	0.42±0.3	0.67±0.1	0.01
Culotte	0.27±0.5	0.48±0.4	0.66±0.2	0.02

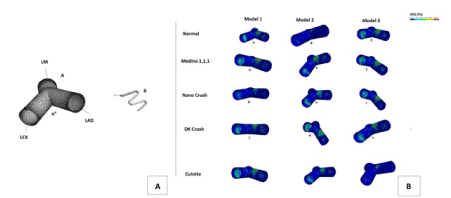
Figure 3. Panel A Stented left main bifurcation : the model after stenting procedure (a) using a third generation 80-micron drug eluting stent (b). Panel B:Tridimensional evaluation of WSS in three angles configurations: model 1 (45°), model 2 (60°) and Model 3 (80°) in the physiologic (normal), pathologic (Medina 1,1,1) and after simulating the three dual stenting techniques, Nano crush, DK crush and Culotte. In the Model 1, the Nano crush technique leads to a substantial improvement of the WSS on both the LAD and LCX walls. Conversely, a less physiological WSS reduction was obtained at the same artery sites using the DK and culotte techniques, respectively. In model 2, despite a good improvement of the WSS using the Nano-crush approach, an area of lower WSS was still present after the stenting in the inferior roof the LCX, probably due to a non-optimal stent apposition at that angle. The same area of lower WSS was also present after the DK stenting, but this was located more centrally on the vessel wall. Conversely, the use of the Culotte stenting removed this area. In the model 3, areas with intermediate values of WSS were still present in the LCX after the stenting with the Nano-crush and culotte techniques. However, the DK crush allows to obtain more physiological values of WSS in the LAD wall. Similarly, the culotte stenting leads to an accepatble physiological WSS configuration in the bifurcation model.

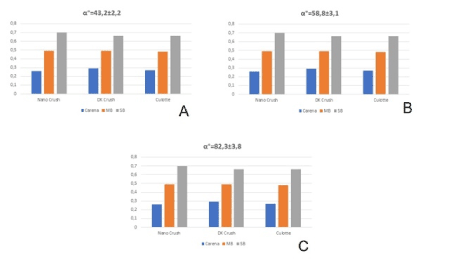
Figure 4. Histograms representation of the averaged WSS  throughout  the three techniques in the three angles configurations. WSS were showed by locations:  Carina, Main branch (MB) and Side branch (SB).

Discussion

Our computational study confirmed that in LM disease, the angle of the bifurcation impacts extensively on the WSS which increased in nominal value as the bifurcation angle increases in both physiological and pathological models. Moreover, angles seem to have an impact on the performance of different techniques in terms of both averaged WSS and lower WSS areas which are again different depending on which segment of the bifurcation is considered.

It is well-known that bifurcations are prone to developing atherosclerosis in regions associated with low wall shear stresses (WSS) and a high oscillatory shear index (OSI) [12]. The physiological effects of wide angles on WSS is a well-known phenomenon occurring when the disturbed flow pattern reduces the wall pressure and the flow changes from the left main stem to the bifurcated regions [1]. Doutel, et al. [13] found that the so-called expansion ratio is the main factor leading to large regions of low WSS in coronary bifurcations: this ratio expresses a relation between the cross-section areas of the outflow branches and the cross-section area of the main branch. Large regions of low WSS are present when high expansion ratios are found. That finding correlates well with the study of Huo, et al. [14] who found that an increase of bifurcation angle (like a decrease of daughter diameters) leads to low WSS and high OSI near the carina, while an increase of daughter diameters (similar to a decrease of bifurcation angle) affects surface regions opposite to the carina.

The role of angles is confirmed and even enhanced in our study which for the first time in literature involve the LM bifurcation (Table 3).

Table 3. Comparison between previous findings and novel findings of the study.

What is known	What the study adds
Bifurcations are prone to develop atherosclerotic lesions in areas with low wall shear stresses (WSS) and a high oscillatory shear index (OSI)	Angles have a mutual impact on WSS in LM bifurcations
Large regions of low WSS correspond to wide angles in non LM bifurcation	Application of Nano crush, DK crush and Culotte different impacts on WSS depending on bifurcation angles
Endovascular stents produce fluid disturbances, modifying wall shear stress distribution which may be responsible for  neointimal hyperplasia after stent placement  as well as stent restenosis and thrombosis	The impact of specific  stenting technique on lower WSS area increase, should probably be explained by both struts’ coverage and  struts apposition to the wall.

While angles play a pivotal role in the atherosclerosis development and maintenance in non-stented coronary artery bifurcation, their influence in stented vessels has not been clarified so far. 

Beier, et al. [15] suggested that other shape characteristics and stent placement/strategy may be more important than bifurcation angles in atherosclerotic disease development, progression, and stent outcome. On the contrary, Chen, et al. [16] found that stenting the main branch at bifurcations with larger SB/MB ratios or smaller SB angles (30°) resulted in lower WSS, higher WSSG, and OSI.

As all past investigations involved non-LM bifurcation, a proper comparison with our data became difficult; however, our study suggested that in LM, angles matter at least as much as the stenting techniques.

Endovascular stents produce fluid disturbances [17,18], which in coronary bifurcations are important in altering the distributions of wall shear stress. WSS alterations predict the sites of neointimal hyperplasia after stent placement [19] and impact on stent restenosis and thrombosis [20,21].

Over the past decade, different stenting strategies have been tested in bifurcation by computational fluid dynamic studies in order both to understand their rheological pitfalls and to explain the clinical poor results of coronary stenting in bifurcations despite the technological advancements.

Double stenting using different lengths of the side branch SB) stent have been tested by Chen, et al. [22], who found that dual stenting with a longer SB stent had the most adverse impact on SB endothelial WSS, WSSG, and OSI, with a low WSS region up to 50% more than the case with a shorter SB stent. They also demonstrated flow disturbances resulting from SB stent struts protruding into the main flow field near the carina, which may have implications on stent thrombosis.

More recently Brindise, et al. [23] investigated provisional side branch, culotte, and crush technique in a computational model of non LM bifurcation. They demonstrated that crush provided good rheology, but demonstrated detrimental stent interactions, whereas provisional side branch and culotte maintained normal flow conditions. However, provisional SB provided about a 300% increase in both OSI and relative residence time (RRT), whereas culotte yielded a 10 and 85% increase in OSI and RRT, respectively.  Our group recently [1] have tested four double stenting techniques including Nanocrush, Culotte, Provisional T, and DK crush in a Left Anterior Descending –Diagonal bifurcation model, confirming and suggesting that techniques which imply more metal layers into the carina have a more detrimental effect on bifurcation rheology and a theoretical increased risk of restenosis and thrombosis. Similarly, a simulation involving the LM and comparing culotte with cross-over stenting confirmed and indirectly suggested that cross-over stenting offers theoretically a more “physiology-adherent” treatment compared to double stenting techniques [24].

The current study represents the first simulation  involving the LM and comparing the effects of LM bifurcation angle on three different double stenting techniques, which are the Nano crush, a technique recently developed in our institution [25], the DK crush, a technique which shows a certain superiority over provisional stenting  in LM [26], and the standard Culotte [27], a well-established technique in LM disease.

Our data showed that angles have a mutual impact on specific technique performance in terms of WSS, as the different impact of each technique on increasing the lower WSS area should probably be explained by not only the grade of struts coverage but also by the strut’s apposition to the wall.

The Nano crush technique has been developed with the aim of being applicable at any bifurcation angle and that is confirmed by our data:  results of averaged WSS were higher in MB and SB at any angle compared to the other two techniques, confirming indirectly the complete coverage and good stent apposition observed in the bench and clinical study [28]. At the carina the WSS are slightly lower at 45°, and highest at 60° and 85° degrees, probably reflecting the larger flow disturbance induced by the short segment of the crushed SB stent at an acute angle. The DK crush showed in our simulation higher values of WSS at the carina at any angle probably reflecting the very good apposition of the stent struts due to the longer segment of the crushed SB stent and the double kissing steps. Conversely, it has the worst results in terms of lower WSS at MB and SB in particular at 60°, something which should be taken into account, since the restenosis usually is located at the SB [29]. Finally, the Culotte had a better performance in terms of WSS in particular at the carina and side branch at 60° degrees, and slightly worse rheolytic profile compared to the other two at 45° and 80° degrees, probably reflecting a suboptimal struts apposition when angles are excessively acute or wide.

Globally the three evaluated techniques had small but significant differences in terms of WSS and lower WSS area; grossly the Nano-crush seems to work more physiologically at angles over 45°, whereas DK crush has a good performance at angles between 45° and 60° degrees. Finally, the Culotte seems to be ideal at angles approaching 60° but less than 85° degrees.

Since lower WSS is implicated in restenosis and thrombosis after stent deployment [19-21], these results appear to be of some importance in understanding points of weakness of such techniques.

Limitations

Our study is limited by a number of limitations. Firstly, it considers virtual left main model. The vessels have been considered non-compliant, straight and with a steady diastolic blood flow in a virtual hemodynamically stable patient. However, coronary artery perfusion is mainly diastolic and previous studies have already demonstrated that myocardial motion has a negligible effect on blood flow distribution on the coronary tree. Secondly, the relative limited numbers of patients enrolled to reconstruct the 3D model should be taken in account as a possible cause of bias. Thirdly, our virtual implantation considered an optimal stent deployment without residual stenosis despite in daily clinical practice, the different angles, the amount and circumferential extent of the calcium, the length of the respective lesion, and many other parameters have an obvious impact on the implantation technique and outcomes. Finally, we did not evaluate the time averaged WSS, oscillatory index, and the relative residence time, which had a recognized role in the development of arterial atherosclerosis.

Conclusions

Our computational fluid dynamic simulation confirmed the role of angles in LM bifurcation physiology and enhanced the impact of bifurcation angles on the performance of main double stenting techniques in terms lower WSS area and averaged WSS. These results should be taken in account in explaining part of the suboptimal clinical outcomes of such techniques in complex LM interventions.

Conflicts of Interest

None to declare

References

1. Chaichana T, Sun Z, Jewkes J (2011) Computation of hemodynamics in the left coronary artery with variable angulations. J Biomech 44: 1869-1878.
2. Moore JE Jr, Timmins LH, Ladisa JF Jr 2010) Coronary artery bifurcation biomechanics and implications for interventional strategies. Catheter Cardiovasc Interv 76: 836-43. [Crossref]
3. Rigatelli G, Zuin M, Dell'Avvocata F, Vassilev D, Daggubati R, et al. (2017) Evaluation of coronary flow conditions in complex coronary artery bifurcations stenting using computational fluid dynamics: Impact of final proximal optimization technique on different double-stent techniques. Cardiovasc Revasc Med 18: 233-240. [Crossref]
4. D'Ascenzo F, Iannaccone M, Giordana F, Chieffo A, Connor SO, et al.  (2016) Provisional vs. two-stent technique for unprotected left main coronary artery disease after ten years follow up: A propensity matched analysis. Int J Cardiol 211: 37-42. [Crossref]
5. Kodumuri V, Balasubramanian S, Vij A, Siddamsetti S, Sethi A, et al. (2018) A Meta-Analysis Comparing Percutaneous Coronary Intervention with Drug-Eluting Stents Versus Coronary Artery Bypass Grafting in Unprotected Left Main Disease. Am J Cardiol 121: 924-933. [Crossref]
6. Kervinen K, Niemelä M, Romppanen H, Erglis A, Kumsars I, et al. (2013) Clinical outcome after crush versus culotte stenting of coronary artery bifurcation lesions: the Nordic Stent Technique Study 36-month follow-up results. JACC Cardiovasc Interv 6: 1160-1165. [Crossref]
7. Cho YI, Kensey KR (1991) Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: steady flows. Biorheology 8: 241–262. [Crossref]
8. Johnston BM, Johnston PR, Corney S, Kilpatrick D (2004) Non-Newtonian blood flow in human right coronary arteries: steady state simulations. J Biomech 37: 709-720. [Crossref]
9. Theodorakakos A, Gavaises M, Andriotis A, Zifan A, Liatsis P, et al. (2008) Simulation of cardiac motion on non-Newtonian, pulsating flow development in the human left anterior descending coronary artery. Phys Med Biol 53: 4875-4979. [Crossref]
10. Nichols WW, O’Rourke MF (1998) The nature of flow of a liquid. In: McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles. 4th ed. London, UK: Arnold, 11–53.
11. Karino T, Goldsmith HL, Motomiya M, Mabuchi S, Sohara Y (1987) Flow patterns in vessels of simple and complex geometries. Ann N Y Acad Sci 516: 422–441. [Crossref]
12. Glagov S, Zarins C, Giddens DP, Ku DN (1988) Hemodynamics and atherosclerosis. Insights and perspectives gained from studies of human arteries. Arch Pathol Lab Med 112: 1018-1031. [Crossref]
13. Doutel E, Pinto SI, Campos JB, Miranda JM (2016) Link between deviations from Murray's Law and occurrence of low wall shear stress regions in the left coronary artery. J Theor Biol 402: 89-99. [Crossref]
14. Huo Y, Finet G, Lefevre T, Louvard Y, Moussa I, et al. (2012) Which diameter and angle rule provides optimal flow patterns in a coronary bifurcation? J Biomech 45: 1273-1279. [Crossref]
15. Beier S, Ormiston J, Webster M, Cater J, Norris S, et al. (2016) Impact of bifurcation angle and other anatomical characteristics on blood flow - A computational study of non-stented and stented coronary arteries. J Biomech 49: 1570-1582. [Crossref]
16. Chen HY, Moussa ID, Davidson C, Kassab GS (2012) Impact of main branch stenting on endothelial shear stress: role of side branch diameter, angle and lesion. J R Soc Interface 9: 1187-1193. [Crossref]
17. Seo T, Schachter LG, Barakat AI (2005) Computational study of fluid mechanical disturbance induced by endovascular stents. Ann Biomed Eng 33: 444-456. [Crossref]
18. Katritsis DG, Theodorakakos A, Pantos I, Gavaises M, Karcanias N, et al. (2012) Flow patterns at stented coronary bifurcations: computational fluid dynamics analysis. Circ Cardiovasc Interv 5: 530-539. [Crossref]
19. LaDisa JF Jr, Olson LE, Douglas HA, Warltier DC, Kersten JR, et al. (2006) Alterations in regional vascular geometry produced by theoretical stent implantation influence distributions of wall shear stress: analysis of a curved coronary artery using 3D computational fluid dynamics modeling. Biomed Eng Online 5: 40. [Crossref]
20. LaDisa JF Jr, Olson LE, Molthen RC, Hettrick DA, Pratt PF, et al. (2005) Alterations in wall shear stress predict sites of neointimal hyperplasia after stent implantation in rabbit iliac arteries. Am J Physiol Heart Circ Physiol 288: H2465-H2475. [Crossref]
21. Koskinas KC, Chatzizisis YS, Antoniadis AP, Giannoglou GD (2012) Role of Endothelial Shear Stress in Stent Restenosis and Thrombosis: Pathophysiologic Mechanisms and Implications for Clinical Translation. J Am Coll Cardiol 59: 1337–1349. [Crossref]
22. Chen HY, Koo BK, Kassab GS (2015) Impact of bifurcation dual stenting on endothelial shear stress. J Appl Physiol (1985) 119: 627-632. [Crossref]
23. Brindise MC, Chiastra C, Burzotta F, Migliavacca F, Vlachos PP (2017) Hemodynamics of Stent Implantation Procedures in Coronary Bifurcations: An In Vitro Study. Ann Biomed Eng 45: 542-553. [Crossref]
24. Rigatelli G, Dell'Avvocata F, Zuin M, Giatti S, Duong K, et al. (2017) Comparative Computed Flow Dynamic Analysis of Different Optimization Techniques in Left Main Either Provisional or Culotte Stenting. J Transl Int Med 5: 205-212. [Crossref]
25. Rigatelli G, Dell'Avvocata F, Zuin M, Vassiliev D, Mazza A, et al. (2017) Complex coronary bifurcation revascularization by means of very minimal crushing and ultrathin biodegradable polymer DES: Feasibility and 1-year outcomes of the "Nano-crush" technique. Cardiovasc Revasc Med 18: 22-27. [Crossref]
26. Chen SL, Zhang JJ, Han Y, Kan J, Chen L, et al. (2017) Double Kissing Crush Versus Provisional Stenting for Left Main Distal Bifurcation Lesions: DKCRUSH-V Randomized Trial. J Am Coll Cardiol 70: 2605-2617. [Crossref]
27. Chen SL, Xu B, Han YL, Sheiban I, Zhang JJ, et al. (2015) Clinical Outcome After DK Crush Versus Culotte Stenting of Distal Left Main Bifurcation Lesions: The 3-Year Follow-Up Results of the DKCRUSH-III Study. JACC Cardiovasc Interv 8: 1335-1342. [Crossref]
28. Rigatelli G, Zuin M, Dell'Avvocata F, Vassilev D, Daggubati R, et al. (2018) Complex coronary bifurcation treatment by a novel stenting technique: Bench test, fluid dynamic study and clinical outcomes. Catheter Cardiovasc Interv [Crossref]
29. Chen SL, Xu B, Han YL, Sheiban I, Zhang JJ, et al. (2013) Comparison of double kissing crush versus Culotte stenting for unprotected distal left main bifurcation lesions: results from a multicenter, randomized, prospective DKCRUSH-III study.  J Am Coll Cardiol 61: 1482-1488. [Crossref]