Take a look at the Recent articles

Abstract

Background: Peripheral arterial disease (PAD) in adults is a common disease associated with older populations who are prone to associated problems such as poor mobility, frailty and de-conditioning if admitted for hospital intervention. Measurement of ambulatory function is indicated for evaluative and predictive reasons although simple functional measure protocols are inconsistent and accuracy/precision performance is unknown. Objectives: In this study standardised protocols and measurement performance data are provided for four temporal metrics (4m gait velocity, 3m timed-up-and-go, timed stair ascent and descent) utilising body-contact as both movement onset and offset events.

Design: A between and within-rater reliability study was undertaken.

Setting: A large acute urban teaching hospital vascular surgery unit.

Methods: A volunteer was videoed performing multiple trials of the four metrics across tempos expected in a PAD population. Four independent physiotherapists of different pay grades timed the videoed events repeatedly. Findings: Accuracy, precision (agreement and reliability) of all functional measures was excellent. Specific caution when employing intra-class correlation coefficient calculations for agreement are detailed.

Conclusion: Simple protocols, which can be utilised in clinical practice, are described with favourable accuracy and precision performance. The use of the protocols in clinical practice will now be able to provide robust functional measurements for discrimination and evaluation in the vascular surgery population.

Key words

Peripheral arterial disease, Gait velocity, vascular surgery

Introduction

Peripheral arterial disease (PAD) is a common yet under-diagnosed phenomenon often manifesting as intermittent claudication during functional ambulation and gait disturbances. Slower self-selected gait velocities exist in those with established disease compared with non-diseased age-matched individuals [1]. Adults with PAD admitted to hospital for surgery are likely to be older and frailer [2,3] increasing the likelihood for significant health care utilisation [4-9] and are prone to hospital acquired deconditioning [10]. Secondary cardiovascular dysfunction due to incurred sedentary behaviour may further reduce physical performance and activities of daily living in this population [1,11].

Early identification of post-operative risk and implementation of preventative strategies reduces length of stay (LOS) in older people [12,13].  This is especially important in a vascular population for two reasons. First, ambulatory function deteriorates prior to the signature surgery and recovery to pre-morbid levels has been found to be sub-optimal [14,15]. Second, vascular inpatients experience prolonged hospital LOS relative to other surgeries in part due to higher proportions of non-elective admissions. For example mean LOS (SD) days for elective/non-elective orthopaedic surgery was 3.3 (0.4) and 5.8 (0.7) respectively, whereas vascular surgery’s was 5.4 (1.1) and 13.8 (3.1) respectively (local data, Guy’s & St Thomas’ NHS Foundation Trust; financial year 2011/12).

A comprehensive meta analysis of older community-dwelling individuals, suggested that patient-reported and objective physical function measures could be used to predict future health states and evaluate performance changes in patients [2], additionally, ubiquitous measures (e.g. gait velocity) were found to be predictive of all-cause mortality. It is important to note however that this study did not include care delivery in acute environments.

Our local urban, acute teaching hospital includes the largest comprehensive vascular surgical department in London(UK). It is established that acute vascular surgery patients present with varied pre and post surgical ambulatory dysfunction, are older, frailer, and expect a relatively long LOS.  It is proposed that simple measures could identify critical individual functional abilities and cue targeted physiotherapy interventions whose efficacy could be subsequently evaluated.  A reliable and easy to use measurement of ambulatory function would be of tremendous benefit in this population. 

Gait velocity (GVel), timed-up-and-go (TUAG) and timed stair ascent and descent (StairA, StairD) are routine tests utilised in clinical practice by physiotherapists.  However published protocols are inconsistent and those available have unreported accuracy and precision metrics.  For example inconsistency prevails in the distance covered in routine GVel, definitive verbal instructions given during TUAG, and in timing onset and offsets particularly, if done at all, in StairA/StairD.

The aims of the present study were: i) To define protocols for GVel, TUAG, StairA and StairD; utilising body-contact events, ii) report on their accuracy with respect to a criterion measure, and iii) report on each protocol’s intra and inter-rater precision.

Methods

Protocols

The final decision on the choice of our measurement protocols was informed by the available literature and the pragmatics of undertaking the measurements during normal clinical practice within the clinical environment.  Details and finalised protocols can be found in the appendix/OLS.

Accuracy & Precision Measurements

We adopted a methodology where repeated measurements of the temporal duration of videoed events of GVel, TUAG, StairA, StairD were undertaken by 4 physiotherapy practitioners. This was primarily in order to ensure variation in the events being measured was negligible [16], and secondarily to mitigate the impracticalities of multiple rating of repeated real-time performances of patients in an acute ward environment.

A volunteer subject (male, age 38), wearing normal clothing and shoes, was used as the subject videoed for all reference events. The project was approved via local service-evaluation governance process (project no: 4746).

The subject was videoed using two identical camcorders (Samsung VP-D362; Samsung Electronics, Chertsey UK, sample rate 50Hz). For GVel and TUAG the cameras were used to include the 4m and 3m runs sagittally from both sides. For the StairA/StairD the cameras captured the start (onset) and the end (offset) of movement, independently, each in the sagittal plane. Protocols were performed at approximations to predetermined tempos with a metronome to guide cadence. Four tempos were chosen to represent our local populations’ performance. We used data measured using our protocols from a retrospective sample of vascular patients (n=266, 71% male, median age (IQR) 75years (68-81)) admitted between May 2011 and May 2012. Tempos were labelled “Vslow” (very-slow), “Slow”, “Natural” and “Fast”. Each of the 4 tempos was approximated by the model 3 times per measurement, producing reference footage for 12 independent tempos per protocol, 48 pieces of footage in total.

The timings of the reference events were determined using independent technology and represented the criterion measurements [17] for accuracy reporting. SIMImotion (Tracksys, Nottingham, UK) is a commercially available video-based movement analysis system that can synchronise video footage and allows 2D analysis of events through digitisation of preselected points.

The subject performed GVel and TUAG in a clinical rehabilitation area using a 4m and 3m run respectively. Four retroreflective markers (12mm diameter) were attached to the shoes using double-sided tape on the most caudal aspect of the mid calcanei and lateral rostral aspects of the foot at positions adjacent to the 5^th metatarsal heads deriving a simple 2-point segment representing each foot.  Lines were marked on the floor at 3m and 4m from the start position line (0m). An additional marker was attached to the palm of an examiner’s hand, which became visible when the tester’s hand was opened on the verbal command “go” for TUAG. The subject performed StairA/StairD with similar foot markers attached, on an internal hospital staircase used with vascular patients (10 steps, 18cm rise, 26cm run, 150cm width, polished concrete, well lit). In all cases the subject selected the leading leg, and commenced movement when ready, except TUAG where they proceed upon hearing an audible “go” signal.

Movement onset/offset events used to determine reference timings are summarised in Table 1. Other than TUAG, all onset events consisted of first-footfall contact by the leading limb (GVel; frame number at first-footfall contact beyond or on the start line determined by frame by frame observation, StairA/StairD; frame number where distal foot marker ceased vertical descent on the first up-stair/down-stair surface respectively). TUAG onset was determined by palm marker exposure. Movement offset for GVel was defined as first-footfall contact beyond end (4m) virtual line (frame number at first-footfall beyond the 4m line determined by frame by frame observation); for TUAG - final seat-contact (frame number at first steady downward movement of pelvis determined by frame by frame observation); and for StairA and StairD - 1^st frame where the distal foot marker on the final limb ceased vertical descent on the top and bottom floor surface respectively.

Table 1: Onset and offset movement timings per protocol.

Protocol	Variable	No. Tempos	No. Events§	Total Events	Movement Onset	Movement Offset
GVeli	Velocity (m.s-1)	4†	3	12	1st FC¶ on/after start line	1st FC¶ on/after end line
TUAGii	Time (s)	4	3	12	Hand open‡	Seat-down
StairAiii	Time (s)	4	3	12	1st FC up-stair surface	2nd FC top surface
StairDiv	Time (s)	4	3	12	1st FC down-stair surface	2nd FC bottom surface
				48
i4m walk; ii3m Timed-up-and-go; iii10 steps Stair Ascent; iv10 steps Stair Descent;†(Fast, Normal, Slow, Vslow); $Videoed per tempo; ¶foot contact, ‡audible “go” used in repeat measures by raters

Final reference tempos are summarised per protocol in Table 2.

Table 2. Actual Tempos.

			GVel (m.s-1)	TUAG (s)	StairA (s)	StairD (s)
Reference Tempos	V slow	1.	0.157	54.56	23.14	26.90
		2.	0.157	60.53	22.66	26.90
		3.	0.157	58.36	22.82	26.96
	Slow	1.	0.317	32.81	12.90	15.04
		2.	0.315	32.63	12.78	15.02
		3.	0.314	32.53	12.76	15.06
	Natural	1.	1.026	8.88	9.18	10.04
		2.	1.067	8.18	9.40	9.88
		3.	1.117	9.23	9.48	10.14
	Fast	1.	1.613	5.40	7.68	7.84
		2.	1.606	6.66	8.20	7.84
		3.	1.581	6.53	7.78	7.84

Each videoed event was duplicated ten times and all duplications randomly edited to a video file for rating per protocol. Four physiotherapists independently rated the 120 randomised footage events per protocol in real-time. Their instructions for the rating were to time each event in sequence, using onset and offset events as described in Table 1.  Figure 1 summarises the repeated ratings undertaken per protocol.

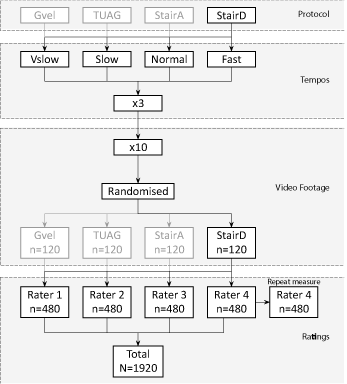
Figure 1. Repeated rating summary; StairD detail highlighted as an example for simplicity.

Raters used a digital stopwatch (EA Combs 898M, EA Combs South Woodford, London, UK) in time sessions allocated within their clinical duties at local Trust PC stations. Four raters (3F, 1M, pay-scale Bands 3-7 [18]) represented the physiotherapists working with vascular inpatients. Mean age was 30 years (SD=5.5), mean physiotherapy experience was 36 months (SD=28.1). All ratings were completed within 2 sessions and total mean rating time was 98min (range 90-120min). One rater repeated the process one week later for intra-rater analysis.

Statistical Analysis

A summary of our adopted nomenclature and analytical methods is presented in Table 3. To establish protocol accuracy and validity, repeated measurements within each individual’s data were compared with criterion values. Mean differences and standard deviations of the mean are reported per tempo for each of the four measurement protocols.

Table 3. Accuracy and precision methods.

	Accuracy	Precision
	Validity	Reliability	Agreement
Inter-Rater 4 raters Repeated measurements	Mean and variation (SD) of difference from reference values	ICC (2,1)	–
Intra-Rater 1 rater Test-Retest	–	ICC (3,1)	95% LOA SEM MDC
LOA – limits of agreement SEM – standard error of the mean MDC – minimal detectable change ICC – intraclass correlation coefficient

To examine relative reliability of the protocols, intra class correlation coefficients (ICCs) were calculated. For intra-rater reliability two-way mixed effects models (ICC(3,1)) were used, and for  inter-rater reliability two-way random effect models (ICC(2,1)) were used [19]. Cut-off values for interpretation of ICCs is a contentious subject (for example see [20]). However Lohr and colleagues advocated that accepted minimal standards for reliability coefficients should be 0.7 for group comparisons and 0.90-0.95 for individual comparisons [21]. We therefore accepted ICC ≥0.9 as excellent and reported 95% confidence intervals (CI).

To assess intra-rater agreement, the videos per protocol were first regarded as being 120 different movement events. Agreement between the repeated measures was assessed using Bland Altman methods [22] with the mean (SD) of the difference between measurements used to determine 95% limits of agreement overall and for each tempo category. In addition, the standard error (SEM) of these data was also calculated as where is the pooled standard deviation of the quantity being studied (i.e. GVel, TUAG, StairA or StairD) and r is an estimate of the correlation between them, here the ICC. SEM is a useful reliability statistic in that it quantifies measurement error in the same units as the measurement. The SEM was also used to calculate the minimum detectable change (MDC) as . Here MDC represents the magnitude of change necessary to exceed the measurement error of two repeated measures at a 95% CI.

Results

Inter-Rater Data

Summary results for inter-observer ratings are shown in Table 4. When all tempos were considered per protocol relative reliability was excellent (ICC = 0.998-1.00). Within each tempo however inconsistent ICCs were obtained the majority of which were poor; for example StairD (ICC=0.058-0.372). This was repeated across all measures except TUAG, which yielded consistently good ICC across all tempos (ICC=0.853-0.998). The gap at StairD represents data that was too homogenous for ICC to be calculated. Accuracy within protocols was rated excellent with variation (SD) in differences from criterion measures remaining relatively small; less than 0.03m.s^-1  for GVel, and all other measures below 0.4s. The notable exception was a SD of 0.854s for fast tempo stair ascent.

Table 4: Inter-rater accuracy and precision summary by tempo

		Accuracy	Precision
			Reliability
Protocol	Tempo	SD*	ICC¶	(95% CI†)
GVel (m.s-1)	V  Slow	0.001	0.997	0.991-0.999
	Slow	0.002	0.413	0.219-0.614
	Natural	0.020	0.545	0.314-0.734
	Fast	0.047	0.087	0.000-0.252
	All	0.026	0.998	0.997-0.999
TUAG (s)	V  Slow	0.114	0.998	0.997-0.999
	Slow	0.135	0.853	0.752-0.921
	Natural	0.109	0.937	0.884-0.968
	Fast	0.118	0.956	0.914-0.978
	All	0.119	1.000	0.999-1.000
StairA (s)	V  Slow	0.106	0.728	0.583-0.843
	Slow	0.113	0.181	0.014-0.345
	Natural	0.091	0.661	0.477-0.806
	Fast	0.854	0.778	0.631-0.879
	All	0.129	1.000	0.999-1.00
StairD (s)	V  Slow	0.211	0.087	0.000-0.268
	Slow	0.305	0.058	0.001-0.202
	Natural	0.164	0.372	0.170-0.585
	Fast	0.130	–	–
	All	0.206	0.999	0.999-0.999
*Standard deviation of difference from reference ¶intraclass correlation coefficient †confidence interval

Inter-rater results per functional measurement across raters are summarised in Table 5 and Table 6. Here mean differences from criterion measures can be interpreted and are all indicative of favourable accuracy. The gaps in the table represent where data was too homogenous for ICC to be calculated as a measure of precision.

Table 5: Accuracy and Precision by Individual Raters per Protocol.

					Precision
			Accuracy		Reliability
Protocol	Pay Grade	Tempo	Mean diff	SD*	ICC¶	(95% CI‡)
GVel (m.s-1)	Band 3	V  Slow	-0.002	0.001	–	–
		Slow	-0.001	0.003	–	–
		Natural	0.007	0.024	0.793	0.610-0.896
		Fast	0.046	0.053	0.170	0.000-0.495
		All	0.015	0.037	0.976	0.965-0.984
	Band 5	V  Slow	-0.003	0.001	–	–
		Slow	-0.011	0.004	–	–
		Natural	0.006	0.016	0.908	0.817-0.955
		Fast	0.213	0.037	0.048	0.000-00397
		All	0.062	0.102	0.986	0.979-0.991
	Band 6	V  Slow	-0.002	0.000	–	–
		Slow	-0.009	0.005	–	–
		Natural	0.038	0.027	0.655	0.390-0.819
		Fast	0.241	0.046	0.229	0.000-0.540
		All	0.081	0.111	0.984	0.976-0.989
	Band 7	V  Slow	-0.003	0.001	–	–
		Slow	-0.011	0.003	–	–
		Natural	0.014	0.025	0.712	0.478-0.852
		Fast	0.242	0.038	0.013	0.000-0.015
		All	0.073	0.114	0.983	0.974-0.988
TUAG (s)	Band 3	V  Slow	2.497	2.497	0.985	0.968-0.993
		Slow	1.973	1.973	0.399	0.051-0.661
		Natural	0.583	0.583	0.940	0.879-0.971
		Fast	0.386	0.386	0.977	0.951-0.989
		All	1.360	1.360	0.999	0.999-0.999
	Band 5	V  Slow	2.455	2.455	0.987	0.972-0.994
		Slow	1.853	1.853	0.526	0.210-0.743
		Natural	0.490	0.490	0.987	0.972-0.994
		Fast	0.283	0.283	0.990	0.978-0.995
		All	1.272	1.272	0.999	0.999-0.999
	Band 6	V  Slow	2.449	2.449	0.984	0.967-0.992
		Slow	1.859	1.859	0.544	0.234-0.753
		Natural	0.504	0.504	0.940	0.878-0.971
		Fast	0.277	0.277	0.979	0.956-0.990
		All	1.272	1.272	0.999	0.999-0.999
	Band 7	V  Slow	2.524	2.524	0.987	0.972-0.994
		Slow	1.969	1.969	0.511	0.191-0.733
		Natural	0.616	0.616	0.971	0.941-0.987
		Fast	0.412	0.412	0.958	0.914-0.980
		All	1.380	1.380	0.999	0.999-0.999
*Standard Deviation †Limits of agreement ¶Intra-class correlation coefficient ‡Confidence interval

Table 6: Accuracy and Precision by Individual Raters per Protocol (StairA, StairD).

			Accuracy		Precision
					Reliability
Protocol	Pay Grade	Tempo	Mean diff	SD*	ICC¶	(95% CI‡)
StairA (s)	Band 3	V  Slow	0.163	0.131	0.661	0.003-0.882
		Slow	0.161	0.097	0.111	0.001-0.367
		Natural	0.087	0.082	0.722	0.083-0.901
		Fast	0.150	0.209	0.964	0.288-0.865
		All	0.140	0.140	0.999	0.998-1.000
	Band 5	V  Slow	0.088	0.160	0.747	0.467-0.881
		Slow	0.089	0.145	0.212	0.002-0.501
		Natural	-0.016	0.119	0.716	0.486-0.854
		Fast	-0.019	0.165	0.833	0.680-0.917
		All	0.035	0.156	1.000	0.999-1.000
	Band 6	V  Slow	0.048	0.115	0.851	0.694-0.928
		Slow	0.037	0.046	0.613	0.145-0.827
		Natural	0.011	0.100	0.753	0.543-0.874
		Fast	0.034	0.059	0.963	0.897-0.985
		All	0.032	0.085	1.000	0.999-1.000
	Band 7	V  Slow	0.116	0.057	0.831	0.001-0.959
		Slow	0.085	0.055	0.335	0.005-0.682
		Natural	0.073	0.076	0.758	0.197-0.911
		Fast	0.094	0.063	0.898	0.106-0.973
		All	0.092	0.064	1.000	0.995-1.000
StairD (s)	Band 3	V  Slow	0.471	0.276	0.015	0.0001-0.149
		Slow	0.315	0.210	–	–
		Natural	0.185	0.180	0.216	0.000-0.514
		Fast	0.008	0.171	–	–
		All	0.245	0.271	0.999	0.993-1.000
	Band 5	V  Slow	0.166	0.579	–	–
		Slow	0.027	0.144	–	–
		Natural	-0.022	0.136	0.645	0.379-0.813
		Fast	-0.051	0.105	–	–
		All	0.030	0.318	0.999	0.999-0.999
	Band 6	V  Slow	0.086	0.157	0.034	0.000-0.336
		Slow	0.088	0.109	–	–
		Natural	0.081	0.083	0.620	0.047-0.845
		Fast	0.060	0.074	–	–
		All	0.079	0.110	1.000	0.999-1.000
	Band 7	V  Slow	0.233	0.080	0.043	0.000-0.190
		Slow	0.199	0.130	–	–
		Natural	0.129	0.073	0.524	0.001-0.831
		Fast	0.145	0.383	–	–
		All	0.177	0.211	0.999	0.997-1.000
*Standard Deviation †Limits of agreement ¶Intra-class correlation coefficient ‡Confidence interval

Relative reliability precision across all tempos remained consistently excellent (ICCs>0.990 per protocol) across all raters.  However when tempos were viewed independently, again there were poor ICCs within grades. To analyse the relative reliability performance across raters, agreement was reassessed across all 10 ratings of each video, rather than treat each video independently. The results are summarised in Table 7 and reveal excellent reliability throughout.

Table 7: ICCs for agreement between 10 ratings of same video.

				Reliability
	Precision
Pay Grade	GVel ICC¶ (95% CI‡)		TAUG ICC (95% CI)		StairA ICC (95% CI)		StairD ICC (95% CI)
Band 7	0.999(0.998-1.000)		0.999(0.999-1.000)		0.999(0.998-1.000)		0.999(0.999-1.000)
Band 6	0.999(0.998-1.000)		0.999(0.999-1.000)		0.999(0.998-1.000)		0.999(0.999-1.000)
Band 5	0.999(0.999-1.000)		0.999(0.999-1.000)		0.999(0.999-1.000)		0.999(0.999-1.000)
Band 3	0.998(0.997-0.999)		0.999(0.999-1.000)		0.998(0.997-0.999)		0.999(0.999-1.000)
¶Intra-class correlation coefficient ‡Confidence interval

Intra-rater Data

One subject repeated measurements 1 week after their initial measurements.  When all tempos were considered per protocol, relative reliability (ICC) was excellent (ICC=0.998-1.00, see Table 8). Within each tempo however inconsistent ICCs were obtained the majority of which were poor, for example StairA (ICC=0.046-0.884). This was repeated across all measures except TUAG, which yielded consistently excellent ICC across all tempos (ICC=0.913-0.998).

Table 8: Intra-rater precision summary by tempo.

		Precision
		Agreement				Reliability
Protocol	Tempo	95% LOA†	(LOA† range)	SEM‡	MDC§	ICC|	(95% CI¶)
GVel (m.s-1)	V  Slow	0.01-0.01	(0.00)	0.002	0.007	0.977	0.993-0.999
	Slow	-0.01-0.01	(0.02)	0.003	0.001	0.368	0.039-0.632
	Natural	-0.05-0.08	(0.13)	0.021	0.058	0.355	0.023-0.623
	Fast	-0.13-0.13	(0.26)	0.046	0.127	0.185	0.000-0.511
	All	-0.07-0.08	(0.15)	0.030	0.083	0.998	0.998-0.999
TUAG (s)	V  Slow	-0.36-0.29	(0.62)	0.324	0.894	0.998	0.997-0.999
	Slow	-0.33-0.23	(0.64)	0.099	0.275	0.913	0.820-0.958
	Natural	-0.44-0.34	(0.75)	0.147	0.406	0.915	0.829-0.958
	Fast	-0.44-0.15	(0.71)	0.144	0.040	0.940	0.634-0.981
	All	-0.40-0.26	(0.66)	0.693	1.912	0.999	0.999-1.000
StairA (s)	V  Slow	-0.22-0.31	(0.53)	0.060	0.166	0.812	0.640-0.906
	Slow	-0.29-0.31	(0.60)	0.149	0.409	0.046	0.000-0.400
	Natural	-0.14-0.27	(0.41)	0.054	0.148	0.739	0.417-0.881
	Fast	-0.18-0.26	(0.44)	0.038	0.105	0.884	0.763-0.944
	All	-0.21-0.29	(0.50)	0.004	0.011	1.000	0.999-1.000
StairD (s)	V  Slow	-0.47-0.65	(1.12)	0.244	0.674	0.270	0.007-0.562
	Slow	-0.40-0.70	(1.10)	0.272	0.751	0.053	0.000-0.358
	Natural	-0.13-0.40	(0.53)	0.101	0.278	0.450	0.005-0.736
	Fast	-0.65-0.85	(1.50)	0.375	1.033	0.043	0.000-0.385
	All	-0.44-0.67	(1.11)	0.009	0.024	0.999	0.999-0.999
*Standard Deviation †Limits of agreement ‡Standard error of measurement §Minimal detectable change |Intra-class correlation coefficient ¶Confidence interval ,

However intra-rater agreement precision was excellent across all measurements and tempos. For gait velocity 95% LOA of -0.07-0.08m.s^-1 across all tempos describes the rater varying less than 0.1m.s^-1 on repeat measurement of the same event indicative of excellent stability of measurement. MDC calculations yielded 0.083m.s^-1 as the minimal magnitude of change with 95% confidence necessary to exceed two repeated measures’ errors. Per tempo, limits of agreement remained excellent and MDC at worst was 0.127m.s^-1 for the fast velocity (Table 8).

Agreement precision for the other timed measures, when considering all tempos, was worst for TUAG (MDC=1.912s) with both stair measurements yielding MDC statistics <0.1s, and StairD yielding the widest LOA (-0.44-0.67s). When considered individually no one tempo demonstrated consistently the widest range of agreement (LOA).

Figure 2 summarises the range of LOA per measurement. StairD represents the largest disagreement yet remains within ±1s. Fast tempo represents the widest range (1.5s), which is intuitive, with proportional errors increasing with reduced event time and is consistent with GVel data. However this is not consistent with StairA or TUAG data.

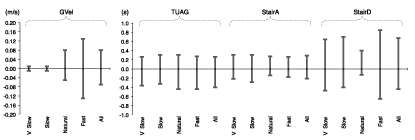
Figure 2. 95% LOA intra-rater precision per tempo per measurement protocol.

Discussion

We have detailed the accuracy and precision of four commonly used, pragmatic, simple and feasible timed clinical performance measure protocols utilising, in the cases of GVel and StairA/StairD foot initial contact events for use in an acute vascular inpatient population. TUAG has always routinely utilised the instance of seat-down as a body-contact on the returning to the chair in its protocols to good effect. However to our knowledge this is the first time protocols using body-contact events have been described in the literature for GVel or temporal stair measures.

Following an agreed protocol standardises the methodology of measurement. Yet it is only when the performance of that standardisation is analysed that protocols can be duly accepted for clinical practice.

Accuracy and precision is fundamental in assessing the suitability of clinical measurement procedures. The former relates to the ability of the procedure to accurately measure what it is supposed to be measuring; the latter that the interpreted results remain consistent between observers and within a single observer. The two terms are synonymous, respectively, with validity and reliability [17,23].

Accuracy

The current study utilised instances of body-contact to provide clinicians with clear and definitive onset and offset timing events because temporal movement measurement is predicated on determining these instances. In physical performance measurement the time period, or its derivative with respect to a known distance as in the case of GVel, becomes the surrogate of the performance behaviour. Comparison of our measurements with criterion values derived from independent technology showed that the accuracy of our measurements was favourable on repeat testing of the same event. This means that timing results reflect reality using our protocols.

While we predicted that these timing events might be clearer to the operator, the risk in our protocols was that body-contact events could be appreciably distant from true onset and offset positions in space and time yielding inaccurate measures. However our findings justified the validity of using foot-contact events in the clinical context for these 4 measures, which include temporal measurement of stair negotiation on runs with typical UK dimensions. These data are therefore generalisable with other similar stair configurations.

Precision

2021 Copyright OAT. All rights reserv

We used intraclass correlation coefficients (ICCs) in addition to Bland’s limits of agreement (LOA) method [22] to assess relative reliability and agreement respectively. This is justified because reliability and agreement parameters of physical-function measurement tools are not pre-set [24]. They are instead an interacting milieu of equipment, the operator, subjects/objects or events, and the context of measurement [24]. Reliability is a performance characteristic of a tool in a certain population sample and its parameters are required for tools used to discriminate subjects (e.g. patients’ functional performance) or objects (e.g. imaging studies) into clinically useful categories [25]. A tool might also need to have proven agreement when it is used to re-measure a subject/object if one uses it to evaluate a meaningful change – often the case in clinical measurement. We considered that reporting both aspects of precision was imperative in line with the considerable debate of how reliability is reported in the literature [17, 24-29].

Our findings however showed that relative reliability when individual tempos were taken into account was variable and in a lot of cases poor. This is because ICCs compare variation between measurements to that between raters. Due to three events within tempos having very low variability we obtained poor ICCs, and makes the inclusion of agreement measures important if misinterpretation of the measurement tool is to be avoided.

Our poor ICCs was likely due to measuring events at 3 independent tempos near a target tempo and hence introducing homogeneity to our data. Interpretation of agreement is fallible when the variance is relatively low using ICCs – its discrimination properties excel in heterogeneous compared to homogenous populations [24,30]. We believe our methodology remains applicable as we  report accuracy and precision covering the spectrum of expected performance and also assess the relative reliability at similar tempos as is typical in clinical practice.

The LOA results indicated excellent agreement however and taken together with the also excellent ICCs when all tempos were considered, the protocols have impressive reliability characteristics. Absolute reliability was also excellent; intra-rater MDC across all tempos in GVel of 0.083m.s^-1 is within the accepted meaningful change of 0.1m.s^-1 [31,32]. Our largest MDC found in TUAG (1.912s) is small when compared to other literature reporting 3.5s in Parkinson’s disease and in older adults [33,34]. Our small MDC is in keeping with the decision to report on repeated measurements of the same events; other studies used repeated patient measurements introducing realistic, but nonetheless greater variation.

Conclusion

We have provided a set of simple protocols for GVel, TUAG, and stair negotiation utilising body-contact events for timing. We have demonstrated excellent accuracy and precision performance based on repeated measures of videoed events. Clinicians should be confident in them being used in clinical practice for both discriminative and evaluative purposes for this complex vascular caseload and in other clinical settings where a similar spectrum of performance variables is apparent.

Ethical approval:

The project was approved via local service-evaluation governance process (project no: 4746).

Conflict of interest:

None declared.

Appendix A:

Supplementary data

View supplementary data

References

1. Crowther RG, Spinks WL, Leicht AS, Quigley F, Golledge J (2007) Relationship between temporal-spatial gait parameters, gait kinematics, walking performance, exercise capacity, and physical activity level in peripheral arterial disease. J Vasc Surg 45: 1172-1178. [CrossRef]
2. Cooper R, Kuh D, Hardy R (2010) Objectively measured physical capability levels and mortality: systematic review and meta-analysis. BMJ 341: c4467. [CrossRef]
3. Hirsch AT, Allison MA, Gomes AS, Corriere MA, Duval S, et al. (2012) A call to action: women and peripheral artery disease: a scientific statement from the American Heart Association. Circulation 125: 1449-1472. [CrossRef]
4. Mahoney EM, Wang K, Keo HH, Duval S, Smolderen KG, et al. (2010) Vascular hospitalization rates and costs in patients with peripheral artery disease in the United States. Circ Cardiovasc Qual Outcomes 3: 642-651. [CrossRef]
5. Makowsky MJ, McAlister FA, Galbraith PD, Southern DA, Ghali WA, et al. (2008) Lower extremity peripheral arterial disease in individuals with coronary artery disease: prognostic importance, care gaps, and impact of therapy. Am Heart J 155: 348-355. [CrossRef]
6. Safley DM, Kennedy KF, Stansby G, Flather M, Cohen DJ, et al. (2011) Prevalence and predictors of persistent health status impairment in patients referred to a vascular clinic with intermittent claudication. Eur J Vasc Endovasc Surg 42: 355-362. [CrossRef]
7. Bennett PC, Gill PS, Silverman S, Blann AD, Chackathayil J, et al. (2011) Hemostatic cardiovascular risk factors, common carotid-intima medial thickness and peripheral arterial disease in South Asians and African Caribbeans: a substudy to the Ethnic-Echocardiographic Heart of England Screening (E-ECHOES) study. J Thromb Haemost 9: 645-652. [CrossRef]
8. Stansby G, Mister R, Fowkes G, Roughton M, Nugara F, et al. (2011) High risk of peripheral arterial disease in the United Kingdom: 2-year results of a prospective registry. Angiology 62: 111-118. [CrossRef]
9. Partridge JS, Harari D, Dhesi JK (2012) Frailty in the older surgical patient: a review. Age Ageing 41: 142-147. [CrossRef]
10. Covinsky KE, Pierluissi E, Johnston CB (2011) Hospitalization-associated disability: "She was probably able to ambulate, but I'm not sure". JAMA 306: 1782-1793. [CrossRef]
11. Milani RV, Lavie CJ (2007) The role of exercise training in peripheral arterial disease. Vasc Med 12: 351-358. [CrossRef]
12. Harari D, Hopper A, Dhesi J, Babic-Illman G, Lockwood L, et al. (2007) Proactive care of older people undergoing surgery ('POPS'): designing, embedding, evaluating and funding a comprehensive geriatric assessment service for older elective surgical patients. Age Ageing 36: 190-196. [CrossRef]
13. Harari D, Martin FC, Buttery A, O'Neill S, Hopper A (2007) The older persons' assessment and liaison team 'OPAL': evaluation of comprehensive geriatric assessment in acute medical inpatients. Age Ageing 36: 670-675. [CrossRef]
14. Czerniecki JM, Turner AP, Williams RM, Hakimi KN, Norvell DC (2012) Mobility changes in individuals with dysvascular amputation from the pre-surgical period to 12 months post amputation. Arch Phys Med Rehabil 93: 1766-1773. [CrossRef]
15. Ambler GK, Dapaah A, Al Zuhir N, Hayes PD, Gohel MS, et al. (2014) Independence and mobility after infrainguinal lower limb bypass surgery for critical limb ischemia. J Vasc Surg 59: 983-987.e2. [CrossRef]
16. Bland JM, Altman DG (1999) Measuring agreement in method comparison studies. Stat Methods Med Res 8: 135-160. [CrossRef]
17. Guyatt G, Walter S, Norman G (1987) Measuring change over time: assessing the usefulness of evaluative instruments. J Chronic Dis 40: 171-178. [CrossRef]
18. NHS Employers. Agenda for Change NHS terms and conditions of service handbook (2010). The NHS Staff Council. Pay circular (AforC) 1/2010: amendment number 16; Part 2: Pay. 2010.
19. Shrout PE, Fleiss JL (1979) Intraclass correlations: uses in assessing rater reliability. Psychol Bull 86: 420-428. [CrossRef]
20. Atkinson G, Nevill AM (1998) Statistical methods for assessing measurement error (reliability) in variables relevant to sports medicine. Sports Med 26: 217-238. [CrossRef]
21. Lohr KN, Aaronson NK, Alonso J, Burnam MA, Patrick DL, et al. (1996) Evaluating quality-of-life and health status instruments: development of scientific review criteria. Clin Ther 18: 979-992. [CrossRef]
22. Bland JM, Altman DG (1986) Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1: 307-310. [CrossRef]
23. Viera AJ, Garrett JM (2005) Understanding interobserver agreement: the kappa statistic. Fam Med 37: 360-363. [CrossRef]
24. Costa-Santos C, Bernardes J, Ayres-de-Campos D, Costa A, Amorim-Costa C (2011) The limits of agreement and the intraclass correlation coefficient may be inconsistent in the interpretation of agreement. J Clin Epidemiol 64: 264-269. [CrossRef]
25. Kottner J, Audige L, Brorson S, Donner A, Gajewski BJ, et al. (2011) Guidelines for Reporting Reliability and Agreement Studies (GRRAS) were proposed. J Clin Epidemiol 64: 96-106. [CrossRef]
26. de Vet HC, Terwee CB, Knol DL, Bouter LM (2006) When to use agreement versus reliability measures. J Clin Epidemiol 59: 1033-1039. [CrossRef]
27. Guyatt GH, Kirshner B, Jaeschke R (1992) A methodologic framework for health status measures: clarity or oversimplification? J Clin Epidemiol 45: 1353-1355. [CrossRef]
28. Guyatt GH, Kirshner B, Jaeschke R (1992) Measuring health status: what are the necessary measurement properties? J Clin Epidemiol 45: 1341-1345. [CrossRef]
29. Kottner J, Streiner DL (2011) The difference between reliability and agreement. J Clin Epidemiol 64: 701-702.
30. Muller R, Buttner P (1994) A critical discussion of intraclass correlation coefficients. Stat Med 13: 2465-2476. [CrossRef]
31. Chui K, Hood E, Klima D (2012) Meaningful Change in Walking Speed. Topics Geriat Rehab 28: 97-103.
32. Fritz S, Lusardi M (2009) White paper: "walking speed: the sixth vital sign". J Geriatr Phys Ther 32: 46-49. [CrossRef]
33. Huang SL, Hsieh CL, Wu RM, Tai CH, Lin CH, et al. (2011) Minimal detectable change of the timed "up & go" test and the dynamic gait index in people with Parkinson disease. Phys Ther 91:114-21. [CrossRef]
34. Mangione KK, Craik RL, McCormick AA, Blevins HL, White MB, et al. (2010) Detectable changes in physical performance measures in elderly African Americans. Phys Ther 90: 921-927. [CrossRef]