The walking velocity is considered as the best characterized objective measure of walking disability in MS. In this work, we present a method to extract spatial or temporal parameters that characterize gait from data collected by a wearable motion sensor. We acquired data on 30 patients diagnosed with MS with different gait impairment levels ranging from none to severe deficits. We measured their hip rotation over time with a wearable motion sensor clipped on their belt while they were instructed to walk a distance of 7.60m twice. We extracted the average duration and angular velocity of the patients’ hip during the walking test from the collected rotation time series. Simple linear regression models demonstrate a good correlation between this parameter and the walking velocity. As the device is affordable and minimally invasive, it could play a key role in the early detection of walking deficits by monitoring gait in in daily life.
clinical outcome, gait monitoring, multiple sclerosis, time series analysis, wearable sensor
Walking dysfunction is one of the most frequent symptoms in multiple sclerosis (MS), often described by the patients themselves as the symptom affecting the most their quality of life [1]. The assessment of walking abilities is therefore naturally a major concern in the monitoring of patients [2]. Existing methods have been validated to provide metrics of ambulation correlated with patients' gait deficits. The timed 25-foot walk (T25FW) test pertains to measuring the time required for a patient to walk 7.60m as fast as possible without running and safely. The walking speed derived from the T25FW test has been described as “the best characterized objective measure of walking disability” in MS [3]. In their review to assess the validity of this test, Robert W. Motl, Jeffrey A. Cohen et al. stated that “synchronizing the T25FW with motion sensor for capturing walking speed in everyday life and the patient’s real environment” constitutes a promising perspective [2]. The validity of digital technologies such as pressure-sensitive walkway [4] and wearable motion sensors [5] to measure spatial or temporal parameters representing gait deficit and walking speed in multiple sclerosis patients has been proven. However, like T25FW test, their use has been restricted to the context of medical consultations because of their cost, their size and/or the number of sensors they require. Therefore, there is still a need to develop methods taking advantage of lightweight devices suitable for a use in daily life to have an objective measurement reflecting walking speed. In this paper, we define two indicators of gait abilities, namely the average duration of a gait cycle and the average angular velocity of the hip during a gait cycle, from rotation time series collected by a single tiny motion sensor clipped on the belt. Due to its size and simplicity, this device is suitable for monitoring gait in daily life. We aim at proving that these indicators can serve as proxies to measure walking speed in everyday life. For this purpose, we measured the hip rotation of 30 patients diagnosed with multiple sclerosis while they were performing the T25FW test as part of their annual clinical evaluation in Nantes hospital between September 2019 and May 2020. We extracted the average duration of a gait cycle and the average angular velocity of the hip from the data and compared them with the actual walking speed obtained using the T25FW measured duration. The article is structured as follow. The first section describes how we compute the two novel proposed indicators from the motion sensor data. The second section presents the experimental design of the study. The third section exposes the results. The fourth and last section provides conclusions, discussions and perspectives.
The sensor we opted for is a 9-axis sensor called MetaMotionR from Mbientlab1 (https://mbientlab.com/metamotionr). This device determines its orientation during time at the frequency F = 100 Hertz in the form of a unit quaternion time series (QTS). This orientation is computed with the software sensor fusion (Bosch sensortech)2 (https://www.bosch-sensortec.com/software-tools/software/sensor-fusion-software/) from the data measured by a 3-axis accelerometer, a 3-axis gyroscope and a 3-axis magnetometer embedded in the device. A unit quaternion can be written as q = (w,x,y,z), with 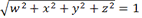 . It represents the direct rotation between (i) the fixed coordinates system (f1,f2,f3) aligned with the Earth coordinates system and (ii) the sensor coordinates system (s1,s2,s3) (Figure 1A and 1B).
. It represents the direct rotation between (i) the fixed coordinates system (f1,f2,f3) aligned with the Earth coordinates system and (ii) the sensor coordinates system (s1,s2,s3) (Figure 1A and 1B).
Quaternions are one way to parameterize a 3-dimensional rotation. It is closely related to the angle-axis representation. In effect, if we let u = (u1,u2,u3) and θ bex respectively (Figure 1A), we have the following relationship:
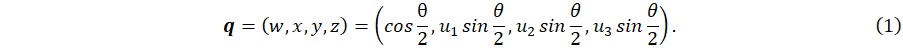
The sensor being clipped at the right side of the belt (Figure 1B), its orientation changes due to the movements of the right hip. The quaternions therefore reflect the rotation of the hip while walking. It is well described that the human gait can be characterized by the repetition of a pattern often coined “Gait Cycle” (GC) [6] as sketched in Figure 2.
The periodicity of the gait signal into GCs naturally applies when monitoring hip rotation while walking (Figure 3A). It is possible to segment the signal into its GC constituents by computing the locations in time when a given foot touches the ground (red points in Figure 3A). The extracted GCs are shown in Figure 3B.
A GC can be denoted by Q = {q1,...,qm}, which represents a time series in which each point qi is the quaternion corresponding to the orientation measured at a time 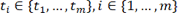 . According to these notations, we can now define for each GC:
. According to these notations, we can now define for each GC:

- the series Δθ = {Δθ1, ... Δθm-1} of angles observed between two successive orientations:
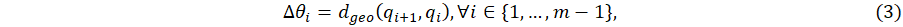
where dgeo(qi+1,qi = 2 cos-1(wi+1wi + xi+1xi + yi+1yi + zi+1zi) is the geodesic distance between two successive quaternions. Next the average angle 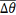 between successive orientations is computed for each GC as the circular mean [7] of Δθ:
between successive orientations is computed for each GC as the circular mean [7] of Δθ:
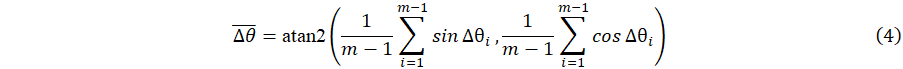
Once quantities T and 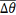 have been computed for each GC, if we assume that a patient performed n GCs, we can define two novel indicators that we claim are good proxies for measuring walking speed:
have been computed for each GC, if we assume that a patient performed n GCs, we can define two novel indicators that we claim are good proxies for measuring walking speed:
- Average duration of a GC:
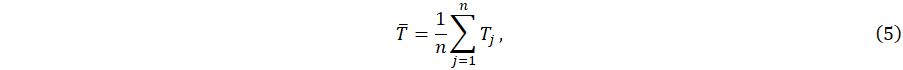
- Average angular velocity of the hip during a GC:
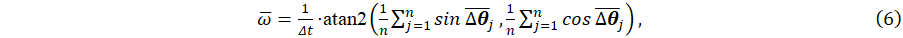
with Δt = F -1 is the constant time step between two measured orientations (in our case, F = 100Hz leading to Δt = 0.01s).
Intuitively, we can hypothesize that these two parameters depend on the patient walking speed. Indeed, the fastest he walked, the shortest his GCs will last and the faster his hip rotate. Observe that eq. (6) could still be used to compute the indicator from a QTS measured on an irregular grid of time points by performing an interpolation of the QTS on a regular grid first.
Material
Data were collected between September 2019 and May 2020 at the University Hospital of Nantes (France) from MS patients that are part of the OFSEP-HD cohort3 (http://www.ofsep.org/en/hd-cohort). Walking data were measured during the T25FW following the test conditions presented in the introduction. The Expanded Disability Status Scale (EDSS) score of each patient was also determined by a neurologist. The EDSS is an ordinal rating scale ranging from 0 to 10 and is a global measure of functional disability, which is not specific to, yet includes, ambulatory deficits [8].
Method
For each patient, the GCs were segmented from data collected by the motion sensor. The two proposed indicators were computed: (i) the average duration 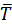 of a gait cycle according to eqs. (2) and (5) and (ii) the average angular velocity
of a gait cycle according to eqs. (2) and (5) and (ii) the average angular velocity 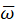 of the hip during a gait cycle according to eqs. (4) and (6). Actual walking speed was computed from the T25FW test duration as the distance of 7.60 m divided by the average time taken by the patient to perform the T25FW test. Variables were described by their mean ± standard deviation (sd) and range. Relationships between the proposed indicators and walking speed were assessed with linear regression adjusted R2 coefficient and Pearson’s linear correlation coefficient r. Statistical significance was claimed when p-value < 0.05 for a two-tailed test. Statistical analyses were performed with the R language, version 4.1.0.
of the hip during a gait cycle according to eqs. (4) and (6). Actual walking speed was computed from the T25FW test duration as the distance of 7.60 m divided by the average time taken by the patient to perform the T25FW test. Variables were described by their mean ± standard deviation (sd) and range. Relationships between the proposed indicators and walking speed were assessed with linear regression adjusted R2 coefficient and Pearson’s linear correlation coefficient r. Statistical significance was claimed when p-value < 0.05 for a two-tailed test. Statistical analyses were performed with the R language, version 4.1.0.
A total of 30 patients were included in the study whose measured data are presented in Table 1. Patients are identified by the letter P followed by a number to preserve their anonymity and ranked in ascending order of EDSS score.
Table 1. Data of the cohort
Patient |
EDSS |
Walking speed (m/s) |
avg. GC angular velocity 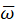 (rad/s), mean ± sd† (rad/s), mean ± sd† |
avg. GC duration 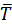 (s), mean ± sd (s), mean ± sd |
P1 |
0 |
2.16 |
2.135 ± 0.321 |
0.76 ± 0.056 |
P2 |
0 |
1.901 |
2.15 ± 0.142 |
0.812 ± 0.079 |
P3 |
0 |
1.81 |
1.915 ± 0.203 |
0.699 ± 0.035 |
P4 |
0 |
1.814 |
1.975 ± 0.192 |
0.743 ± 0.046 |
P5 |
0 |
1.557 |
1.629 ± 0.146 |
0.809 ± 0.032 |
P6 |
0 |
1.743 |
2.37 ± 0.181 |
0.749 ± 0.065 |
P7 |
0 |
1.974 |
2.469 ± 0.106 |
0.837 ± 0.033 |
P8 |
1 |
1.667 |
1.536 ± 0.122 |
0.828 ± 0.043 |
P9 |
1 |
1.506 |
1.337 ± 0.165 |
0.935 ± 0.03 |
P10 |
1 |
1.9 |
3.167 ± 0.161 |
0.719 ± 0.02 |
P11 |
1.5 |
1.639 |
1.581 ± 0.094 |
0.861 ± 0.041 |
P12 |
2 |
1.678 |
2.083 ± 0.254 |
0.992 ± 0.033 |
P13 |
2 |
1.222 |
1.099 ± 0.061 |
1.064 ± 0.014 |
P14 |
2 |
1.458 |
1.298 ± 0.096 |
0.98 ± 0.037 |
P15 |
2 |
1.148 |
1.149 ± 0.07 |
0.951 ± 0.041 |
P16 |
2 |
0.59 |
0.171 ± 0.073 |
2.062 ± 0.699 |
P17 |
2.5 |
1.812 |
1.249 ± 0.187 |
0.894 ± 0.132 |
P18 |
2.5 |
1.731 |
2.131 ± 0.219 |
0.758 ± 0.03 |
P19 |
2.5 |
0.966 |
0.649 ± 0.042 |
1.25 ± 0.071 |
P20 |
2.5 |
0.839 |
0.734 ± 0.062 |
1.122 ± 0.186 |
P21 |
2.5 |
1.745 |
1.831 ± 0.096 |
0.82 ± 0.018 |
P22 |
3 |
1.491 |
1.04 ± 0.117 |
0.925 ± 0.091 |
P23 |
3 |
1.591 |
1.599 ± 0.142 |
0.932 ± 0.024 |
P24 |
4 |
1.124 |
0.74 ± 0.053 |
1.018 ± 0.074 |
P25 |
4 |
1.071 |
1.172 ± 0.231 |
1.031 ± 0.173 |
P26 |
4 |
1.506 |
0.888 ± 0.092 |
0.903 ± 0.156 |
P27 |
4 |
1.057 |
1.023 ± 0.097 |
1.042 ± 0.046 |
P28 |
5.5 |
0.78 |
0.927 ± 0.033 |
1.294 ± 0.135 |
P29 |
6 |
0.763 |
1.066 ± 0.144 |
1.141 ± 0.155 |
P30 |
6 |
0.364 |
0.448 ± 0.037 |
2.342 ± 0.304 |
avg: average, sd: standard deviation, †: standard deviation for circular data [7]
11 patients presented no functional disability (EDSS=0.0-1.5), 12 minimal to moderate disability (EDSS=2.0-3.5) and 7 significant to severe disabilities (EDSS=4.0-6). Table 2 provides a summary of the cohort.
Table 2. Description of patients characteristics and walking parameters
EDSS, median (range) |
2 (0 – 6) |
Walking speed (m/s), mean ± sd (range) |
1.42 ± 0.45 (0.36 – 2.16) |
avg. GC angular velocity 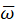 (rad/s), mean ± sd† (range) (rad/s), mean ± sd† (range) |
1.45 ± 0.67 (0.17 – 3.17) |
avg. GC duration 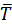 (s), mean ± sd (range) (s), mean ± sd (range) |
0.97 ± 0.31 (0.70 – 2.34) |
avg: average, sd: standard deviation, †: standard deviation for circular data [7]
Figure 4 depicts the relationship between walking speed and the average angular velocity 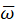 (Figure 4A) and the average duration
(Figure 4A) and the average duration 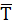 (Figure 4B). The latter plot was drawn in logarithmic scale to enhance visibility. The regression line and its 95% confidence interval are represented by the black line and the grey area respectively.
(Figure 4B). The latter plot was drawn in logarithmic scale to enhance visibility. The regression line and its 95% confidence interval are represented by the black line and the grey area respectively.
The results of the associated Pearson’s correlation test are presented in Table 3. Both average duration 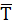 and average angular velocity
and average angular velocity 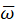 were significantly correlated with walking speed, with estimated Pearson’s coefficients of -0.94 and 0.84 respectively and adjusted R2 coefficient of 0.87 and 0.70 respectively. To summarize, the fastest patients exhibit the smallest average cycle duration and the highest average hip angular velocity.
were significantly correlated with walking speed, with estimated Pearson’s coefficients of -0.94 and 0.84 respectively and adjusted R2 coefficient of 0.87 and 0.70 respectively. To summarize, the fastest patients exhibit the smallest average cycle duration and the highest average hip angular velocity.
Table 3. Bivariate relationship coefficients with walking speed
Parameters |
r |
Adjusted R2 |
avg. GC duration 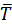 |
-0.94***, (log) |
0.87(log) |
avg. GC angular velocity 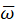 |
0.84*** |
0.70 |
avg: average; r: Pearson’s correlation coefficient; ***: p-value < 0,0001; (log): logarithm transformation of the variable
These results are a first proof of the feasibility to define indicators from a motion sensor wearable in daily life that can serve as proxy to measure walking speed. The average gait cycles duration and angular velocity can be measured with a low computational cost and the data can be streamed from the sensor into a smartphone via Bluetooth. The quality of the results is very encouraging and promising. The correlation between walking speed and gait cycle duration was expected, as it has been shown in several research articles that both are associated with MS severity [9-11]. A study also identified a relationship between spatial and temporal parameters relative to the hip motion and MS severity [10]. However, direct correlation between MS patient’s walking speed and hip angular velocity has not yet been described in the literature to the best of our knowledge. This is key to using hip angular velocity as a proxy to measure walking speed in everyday life.
Other studies identified differences in gait parameters between groups of clinically similar patients [9,11-13], where clinical similarity is assessed through a score such as the EDSS score. However, this score has been criticized for its lack of inter-rater reliability [14] and it represents an assessment of global disability, not only gait abnormalities [8]. Thus, we choose to target walking speed as this outcome is quantitative, objective and directly related to the severity of the gait disability. Another advantage of our method is the use of a single and lightweight device clipped at the belt. It is more affordable, easier to manipulate and more suitable for use in everyday life than methods involving non-wearable systems [10,15] or multiple devices [16], although these approaches may allow for a more complete characterization of an individual’s gait.
Future research may include the evaluation of the reliability of the method and the confirmation of these results on a larger cohort, including comparison with healthy control subjects. The correlation between parameters and walking speed should also be evaluated for different stages of the pathology, as it has been noted that algorithms accuracy may decrease in patient with more severe disability [17].
The natural next development step will be to use the device to collect patients' walking data in daily life to remove evaluation bias and allow early detection of walking deficiencies. This step will require automating the method presented in this article by combining it, for example, with human activity recognition algorithms to identify walking phases in data measured during a full day.
A recent research article proposes a similar approach using a 3-axis accelerometer attached at the lower-back with surgical tape. The authors explain that their prediction of walking speed on patients was poor but spectacularly improved when building a personalized model for each participant using machine learning algorithms. In our proposed method, simple linear regression models were used to predict walking speed from the two indicators derived from hip rotation data and already exhibit good predictions suggesting that looking at rotation data instead of only acceleration data provides critical additional information for monitoring gait. Future research could include building personalized models using machine learning algorithms to further improve walking speed predictions but also more simple analytical models as well to enhance interpretability. In effect, personalized models tend to be sensitive to changes in individual gait characteristics over time which often requires periodic recalibrations [18].
The authors gratefully thank the Observatoire Français de la Sclérose en Plaques group (OFSEP) as well as the clinical research staff of the University Hospital of Nantes and the patients who all immensely helped in collecting the data for this project.
This study was funded by the ARSEP foundation (Fondation pour l’Aide à la Recherche sur la Sclérose En Plaques).
- LaRocca NG (2011) Impact of walking impairment in multiple sclerosis. The Patient: Patient-Centered Outcomes Research 4: 189-201.
- Motl RW, Cohen JA, Benedict R, Phillips G, LaRocca N, et al. (2017) Validity of the timed 25-foot walk as an ambulatory performance outcome measure for multiple sclerosis. Multiple Sclerosis Journal 23: 704-710.
- Bernd C Kieseier, Carlo Pozzilli (2012) Assessing walking disability in multiple sclerosis. Mult Scler 18: 914-924. [Crossref]
- Lizrova Preiningerova J, Novotna K, Rusz J, Sucha L, Ruzicka E, et al. (2015) Spatial and temporal characteristics of gait as outcome measures in multiple sclerosis (EDSS 0 to 6.5). J NeuroEngineering Rehabil 12: 14.
- Angelini L, Hodgkinson W, Smith C, Dodd JM, Sharrack B, et al. (2020) Wearable sensors can reliably quantify gait alterations associated with disability in people with progressive multiple sclerosis in a clinical setting. J Neurol 267: 2897-2909.
- Helwig NE, Hong S, Hsiao-Wecksler ET, Polk JD (2011) Methods to temporally align gait cycle data. Journal of Biomechanics 44: 561-566. [Crossref]
- Jammalamadaka SR, Sengupta A (2001) Topics in circular statistics. World Scientific.
- Kurtzke JF (1983) Rating neurologic impairment in multiple sclerosis: an expanded disability status scale (EDSS). Neurology 33: 1444-1444.
- Flachenecker F, Gaßner H, Hannik J, Lee DH, Flachenecker P, et al. (2020) Objective sensor-based gait measures reflect motor impairment in multiple sclerosis patients: Reliability and clinical validation of a wearable sensor device. Multiple Sclerosis and Related Disorders 39: 101903.
- Severini G, Manca M, Ferraresi G, Caniatti LM, Cosma M, et al. (2017) Evaluation of Clinical Gait Analysis parameters in patients affected by Multiple Sclerosis: Analysis of kinematics. Clinical Biomechanics 45: 1-8. [Crossref]
- Moon Y, McGinnis RS, Seagers K, Motl RW, Sheth N, et al. (2017) Monitoring gait in multiple sclerosis with novel wearable motion sensors. PLOS ONE 12: e0171346.
- Pau M, Caggiari S, Mura A, Corona F, Leban B, et al. (2016) Clinical assessment of gait in individuals with multiple sclerosis using wearable inertial sensors: Comparison with patient-based measure. Multiple Sclerosis and Related Disorders 10: 187-191.
- Müller R, Hamacher D, Hansen S, Oschmann P, Keune PM (2021) Wearable inertial sensors are highly sensitive in the detection of gait disturbances and fatigue at early stages of multiple sclerosis. BMC Neurology 21: 337.
- Cohen M, Bresch S, Thommel Rocchi O, Morain E, Benoit J, et al. (2021) Should we still only rely on EDSS to evaluate disability in multiple sclerosis patients? A study of inter and intra rater reliability. Multiple Sclerosis and Related Disorders 54: 103144.
- Smith VM, Varsanik JS, Walker RA, Russo AW, Patel KR, et al. (2018) Movement measurements at home for multiple sclerosis: walking speed measured by a novel ambient measurement system. Multiple Sclerosis Journal - Experimental, Translational and Clinical 4: 2055217317753465. [Crossref]
- Craig JJ, Bruetsch AP, Lynch SG, Horak FB, Huisinga JM (2017) Instrumented balance and walking assessments in persons with multiple sclerosis show strong test-retest reliability. J NeuroEngineering Rehabil 14: 43. [Crossref]
- Motl RW, Weikert M, Suh Y, Sosnoff JJ, Pula J, et al. (2012) Accuracy of the actibelt® accelerometer for measuring walking speed in a controlled environment among persons with multiple sclerosis. Gait & Posture 35: 192-196.
- Supratak A, Datta G, Gafson AR, Nicholas R, Guo Y (2018) Remote Monitoring in the Home Validates Clinical Gait Measures for Multiple Sclerosis. Frontiers in Neurology 9: 561. [Crossref]
Editorial Information
Editor-in-Chief
Prof. Hamid Yahya Husain
Dubai Health Authority, Dubai
Article Type
Research Article
Publication history
Received date: January 07, 2022
Accepted date: January 20, 2022
Published date: January 28, 2022
Copyright
©2022 Pierre Drouin, Aymeric Stamm, Laurent Chevreuil, Vincent Graillot, Laetitia Barbin, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Citation
Pierre Drouin (2022) Gait impairment monitoring in multiple sclerosis using a wearable motion sensor. Med Case Rep Rev, 2022 DOI: 10.15761/MCRR.1000175

Figure 1. MetaMotionR

Figure 2. Gait cycle
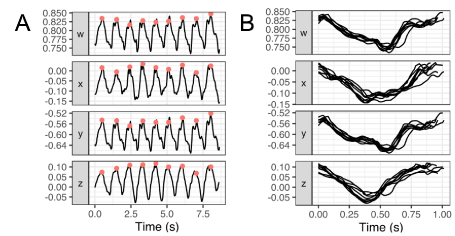
Figure 3. Example of IMU Data and gait cycles detection
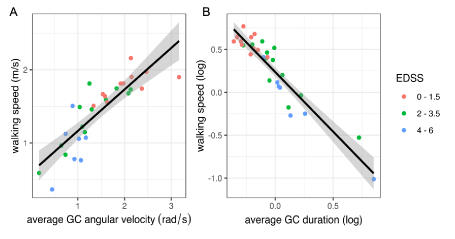
Figure 4. Relationship between parameters and walking speed
Table 1. Data of the cohort
Patient |
EDSS |
Walking speed (m/s) |
avg. GC angular velocity  (rad/s), mean ± sd† (rad/s), mean ± sd† |
avg. GC duration 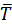 (s), mean ± sd (s), mean ± sd |
P1 |
0 |
2.16 |
2.135 ± 0.321 |
0.76 ± 0.056 |
P2 |
0 |
1.901 |
2.15 ± 0.142 |
0.812 ± 0.079 |
P3 |
0 |
1.81 |
1.915 ± 0.203 |
0.699 ± 0.035 |
P4 |
0 |
1.814 |
1.975 ± 0.192 |
0.743 ± 0.046 |
P5 |
0 |
1.557 |
1.629 ± 0.146 |
0.809 ± 0.032 |
P6 |
0 |
1.743 |
2.37 ± 0.181 |
0.749 ± 0.065 |
P7 |
0 |
1.974 |
2.469 ± 0.106 |
0.837 ± 0.033 |
P8 |
1 |
1.667 |
1.536 ± 0.122 |
0.828 ± 0.043 |
P9 |
1 |
1.506 |
1.337 ± 0.165 |
0.935 ± 0.03 |
P10 |
1 |
1.9 |
3.167 ± 0.161 |
0.719 ± 0.02 |
P11 |
1.5 |
1.639 |
1.581 ± 0.094 |
0.861 ± 0.041 |
P12 |
2 |
1.678 |
2.083 ± 0.254 |
0.992 ± 0.033 |
P13 |
2 |
1.222 |
1.099 ± 0.061 |
1.064 ± 0.014 |
P14 |
2 |
1.458 |
1.298 ± 0.096 |
0.98 ± 0.037 |
P15 |
2 |
1.148 |
1.149 ± 0.07 |
0.951 ± 0.041 |
P16 |
2 |
0.59 |
0.171 ± 0.073 |
2.062 ± 0.699 |
P17 |
2.5 |
1.812 |
1.249 ± 0.187 |
0.894 ± 0.132 |
P18 |
2.5 |
1.731 |
2.131 ± 0.219 |
0.758 ± 0.03 |
P19 |
2.5 |
0.966 |
0.649 ± 0.042 |
1.25 ± 0.071 |
P20 |
2.5 |
0.839 |
0.734 ± 0.062 |
1.122 ± 0.186 |
P21 |
2.5 |
1.745 |
1.831 ± 0.096 |
0.82 ± 0.018 |
P22 |
3 |
1.491 |
1.04 ± 0.117 |
0.925 ± 0.091 |
P23 |
3 |
1.591 |
1.599 ± 0.142 |
0.932 ± 0.024 |
P24 |
4 |
1.124 |
0.74 ± 0.053 |
1.018 ± 0.074 |
P25 |
4 |
1.071 |
1.172 ± 0.231 |
1.031 ± 0.173 |
P26 |
4 |
1.506 |
0.888 ± 0.092 |
0.903 ± 0.156 |
P27 |
4 |
1.057 |
1.023 ± 0.097 |
1.042 ± 0.046 |
P28 |
5.5 |
0.78 |
0.927 ± 0.033 |
1.294 ± 0.135 |
P29 |
6 |
0.763 |
1.066 ± 0.144 |
1.141 ± 0.155 |
P30 |
6 |
0.364 |
0.448 ± 0.037 |
2.342 ± 0.304 |
avg: average, sd: standard deviation, †: standard deviation for circular data [7]
Table 2. Description of patients characteristics and walking parameters
EDSS, median (range) |
2 (0 – 6) |
Walking speed (m/s), mean ± sd (range) |
1.42 ± 0.45 (0.36 – 2.16) |
avg. GC angular velocity 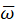 (rad/s), mean ± sd† (range) (rad/s), mean ± sd† (range) |
1.45 ± 0.67 (0.17 – 3.17) |
avg. GC duration 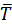 (s), mean ± sd (range) (s), mean ± sd (range) |
0.97 ± 0.31 (0.70 – 2.34) |
avg: average, sd: standard deviation, †: standard deviation for circular data [7]
Table 3. Bivariate relationship coefficients with walking speed
Parameters |
r |
Adjusted R2 |
avg. GC duration 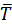 |
-0.94***, (log) |
0.87(log) |
avg. GC angular velocity 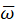 |
0.84*** |
0.70 |
avg: average; r: Pearson’s correlation coefficient; ***: p-value < 0,0001; (log): logarithm transformation of the variable

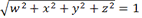 . It represents the direct rotation between (i) the fixed coordinates system (f1,f2,f3) aligned with the Earth coordinates system and (ii) the sensor coordinates system (s1,s2,s3) (Figure 1A and 1B).
. It represents the direct rotation between (i) the fixed coordinates system (f1,f2,f3) aligned with the Earth coordinates system and (ii) the sensor coordinates system (s1,s2,s3) (Figure 1A and 1B).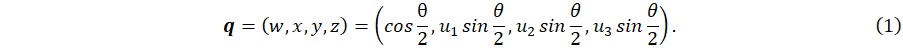
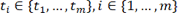 . According to these notations, we can now define for each GC:
. According to these notations, we can now define for each GC:
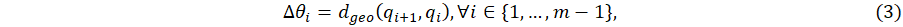
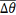 between successive orientations is computed for each GC as the circular mean [7] of Δθ:
between successive orientations is computed for each GC as the circular mean [7] of Δθ: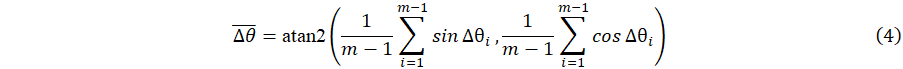
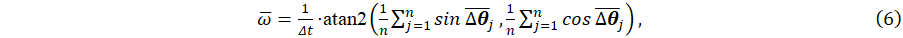
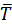 of a gait cycle according to eqs. (2) and (5) and (ii) the average angular velocity
of a gait cycle according to eqs. (2) and (5) and (ii) the average angular velocity 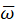 of the hip during a gait cycle according to eqs. (4) and (6). Actual walking speed was computed from the T25FW test duration as the distance of 7.60 m divided by the average time taken by the patient to perform the T25FW test. Variables were described by their mean ± standard deviation (sd) and range. Relationships between the proposed indicators and walking speed were assessed with linear regression adjusted R2 coefficient and Pearson’s linear correlation coefficient r. Statistical significance was claimed when p-value < 0.05 for a two-tailed test. Statistical analyses were performed with the R language, version 4.1.0.
of the hip during a gait cycle according to eqs. (4) and (6). Actual walking speed was computed from the T25FW test duration as the distance of 7.60 m divided by the average time taken by the patient to perform the T25FW test. Variables were described by their mean ± standard deviation (sd) and range. Relationships between the proposed indicators and walking speed were assessed with linear regression adjusted R2 coefficient and Pearson’s linear correlation coefficient r. Statistical significance was claimed when p-value < 0.05 for a two-tailed test. Statistical analyses were performed with the R language, version 4.1.0.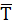 (Figure 4B). The latter plot was drawn in logarithmic scale to enhance visibility. The regression line and its 95% confidence interval are represented by the black line and the grey area respectively.
(Figure 4B). The latter plot was drawn in logarithmic scale to enhance visibility. The regression line and its 95% confidence interval are represented by the black line and the grey area respectively.


