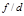Purpose: In general, there is a reciprocal relationship between the width and flux from an x-ray focal spot (corresponding to spatial resolution and photon noise), so that large focal spots are eschewed in computed tomography (CT) and projection and CT mammography. We wish to overcome this limitation. The goal of foxel based computed tomography (FoxelCT) is to achieve spatial resolution limited by the detector pixel size rather than the focal spot size, and therefore permit the use of much smaller detector pixels and/or larger focal spots in clinical CT.
Methods: Rather than using the standard approach of treating the x-ray source as a point, we digitally represent the focal spot as an emission picture consisting of pixels we call foxels (FOcal spot piXELS). Intersections of foxel rays with reconstruction voxels are approximated using the Wu antialiasing line drawing algorithm. All foxel rays in the x-ray light field impinging on a given detector pixel are, in effect, lumped together into a single “passage” or compound ray sum. In this introductory paper noise and other effects that degrade CT are not considered allowing us to demonstrate the upper bound of improvement afforded by the geometry of foxels. The FoxelCT algorithm is a generalization of MART (Multiplicative ART).
Results: We show, by simulating a fan beam body scanner configuration, that the loss in resolution versus focal spot size is much slower using foxels compared to the loss when representing the focal spot as a point source. For any given focal spot size, approximating it as a point is always worse than using foxels and furthermore introduces anatomical distortions.
Conclusions: Foxels permit the use of larger focal spots and thus greater x-ray photon flux with little loss of resolution. Future scanners could take advantage of foxels to increase the ratio of focal spot size to detector pixel size, via bigger focal spots and/or smaller detector pixels. Existing scanners could be immediately enhanced in image quality via incorporation of foxels in their software. Foxels are applicable to any form of radiological imaging that uses focal spots of finite width, including multisource scanners.
The first experimental CT (computed tomography) scanner used a single 1/3 mm x 2.5 cm detector[1, 2], while the first commercial CT scanner a decade later produced images of 80x80 pixels across the head[3] with two 1 mm x 1 cm detectors. Despite the passage of 56 years, clinical CT scanners still use detectors that are about 1 mm in the smallest dimension[4]. They generally do not take advantage of advances in reduced detector pixel width from the fields of digital radiography, microtomography and nanotomography (Figure 1, Table 1). The primary reason for this is that focal spots substantially smaller than 1 mm do not deliver enough x-ray flux for body scanning. Thus, the body CT detector pixel size has been wed to this relatively large focal spot size. Our goal here is to demonstrate a new CT algorithm, FoxelCT, which permits a larger ratio of focal spot size to detector pixel size. Thus, smaller detector pixels and/or larger focal spots may now be used.
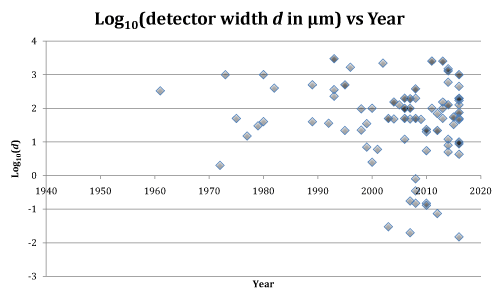
Figure 1. Detector width d in µm on a logarithmic scale versus year. Since the turn of the century, a substantial reduction in x-ray detector size has occurred, driven mostly by microtomography for small animals and nanotomography using synchrotrons. For references from which the data was gleaned, please see Table 1.
Table 1. X-ray detector sizes and focal spot sizes versus year published. Simulation studies are included where physical sizes are mentioned, as dimensions are usually based on available technology. Detector sizes are physical sizes, not binned groups of them. The smallest sizes reported are via “indirect detection”[5], where x-ray photons are converted to light and the flux measured via light microscopy and a digital camera, producing an “effective” detector pixel size much smaller than that of the camera. While this would seem to compromise field of view, one could imagine a CT gantry consisting of an array of such microscopes combined with CT algorithms that work well with a limited number of angles. We do not deal with issues of crosstalk between neighboring detector pixels and attempts to overcome it by achieving subpixel detector resolution[6]. Some overmagnification relative to the Nyquist limit may occur, but is ignored here because of prospects for superresolution[7, 8]. Where a range of focal spot sizes are reported, for a given detector size, the lowest and highest focal spot sizes are listed here. Note that the commercially reported sizes of focal spots at least used to be substantially underestimated[9-13], so that some of the values reported here for focal spot width f could be raised by a factor of up to 2.2[13-17]. On the other hand, the standard pinhole method and others[18] may overestimate[19, 20] or underestimate[20] the focal spot size, so we do not here try to correct any reported values. See[21] for a recent discussion of nominal versus actual focal spot sizes. For small, roughly rectangular focal spots, the smaller width is listed here. However, since we are suggesting that larger focal spots are useful, for rectangular focal spots that are over 1 mm in one dimension, we give that larger dimension. X-ray sources vary from standard x-ray tubes to synchrotron, high-harmonic upconversion (HHG) x-ray lasers and sharp needle emission sources. Sources are listed without regard to whether hard or soft x-rays are produced, and whether monochromatic or broad spectrum. For synchrotrons, the focal spot size is taken as the diameter of the pinhole confining the low angular divergence x-ray beam, which, for example, may travel 27 m before striking the object being examined[22]. Sizes of gantries vary from synchrotron beam lines to body scanners to microtomography and nanotomography, with assorted technologies, with or without gratings. These comparisons, of course, leave out a huge number of variables, including depth of focus[23], wavelength or photon energy, contrast, field of view, region of interest imaging, detector lag, detector crosstalk, number of CT projections, angular dependence of the focal spot shape, the heel effect, beam hardening, beam intensity, exposure time, source to specimen distance, specimen to detector distance, magnification, scatter, voxel size, and composition, size and opacity of the specimen, etc. Nevertheless, the wide scatter in the ratio of focal spot width 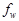 to detector width d suggests a general lack of optimization of this ratio. Ratios in review articles may not be for the same pieces of equipment, as both parameters are rarely reported together, but are included, since the measurements reviewed represent a range of possibilities. “CT” refers to any computed tomography technology, whether clinical or experimental, including tomosynthesis. The larger the ratio of focal spot width f to gantry diameter 2r (distance between the x-ray source and the detector), converted here to
to detector width d suggests a general lack of optimization of this ratio. Ratios in review articles may not be for the same pieces of equipment, as both parameters are rarely reported together, but are included, since the measurements reviewed represent a range of possibilities. “CT” refers to any computed tomography technology, whether clinical or experimental, including tomosynthesis. The larger the ratio of focal spot width f to gantry diameter 2r (distance between the x-ray source and the detector), converted here to 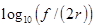 , the greater the angular difference would be between foxel rays and the central ray from a point source. This may be taken as a measure of the effectiveness of using foxels, because the larger the value, the more foxel rays will differ from rays from a point source. The position of the object or patient with respect to the x-ray source and detectors, often used to increase magnification or sharpness, respectively, is not taken into account here, to allow a one dimensional comparison. For a plot of number of slices versus year for clinical CT scanners, see[24].
, the greater the angular difference would be between foxel rays and the central ray from a point source. This may be taken as a measure of the effectiveness of using foxels, because the larger the value, the more foxel rays will differ from rays from a point source. The position of the object or patient with respect to the x-ray source and detectors, often used to increase magnification or sharpness, respectively, is not taken into account here, to allow a one dimensional comparison. For a plot of number of slices versus year for clinical CT scanners, see[24].
Year |
Detector
width d in µm |
Focal spot width f
in µm |
Ratio
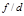
|
Gantry diameter
2r in m |
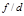
|
CT |
Reference |
1943 |
|
300 |
|
|
|
|
[25, 26] |
1950 |
|
4900 |
|
|
|
|
[27] |
1951 |
|
2000 |
|
|
|
|
[28] |
1955 |
|
2340 |
|
|
|
|
[29] |
1955 |
|
3000 |
|
|
|
|
[29] |
1956 |
|
300 |
|
|
|
|
[30] |
1957 |
|
130 |
|
|
|
|
[31] |
1957 |
|
300 |
|
|
|
|
[32] |
1957 |
|
310 |
|
|
|
|
[31] |
1957 |
|
1200 |
|
|
|
|
[33] |
1958 |
|
400 |
|
|
|
|
[15] |
1958 |
|
16000 |
|
|
|
|
[15] |
1961 |
333 |
333 |
1.0 |
0.30 |
-2.95 |
√ |
[1] |
1964 |
|
1000 |
|
|
|
|
[34] |
1964 |
|
2000 |
|
|
|
|
[34] |
1965 |
|
2000 |
|
|
|
|
[35] |
1968 |
|
1000 |
|
|
|
|
[36] |
1968 |
|
2000 |
|
|
|
|
[36] |
1969 |
|
50 |
|
|
|
|
[37] |
1969 |
|
340 |
|
|
|
|
[37] |
1969 |
|
360 |
|
|
|
|
[38] |
1969 |
|
500 |
|
|
|
|
[39] |
1969 |
|
1000 |
|
|
|
|
[38] |
1969 |
|
2000 |
|
|
|
|
[40] |
1970 |
|
50 |
|
|
|
|
[41] |
1970 |
|
300 |
|
|
|
|
[14] |
1970 |
|
2000 |
|
|
|
|
[14] |
1971 |
|
60 |
|
|
|
|
[42] |
1971 |
|
270 |
|
|
|
|
[19] |
1971 |
|
300 |
|
|
|
|
[42] |
1971 |
|
1000 |
|
|
|
|
[42] |
1972 |
2 |
2 |
1.0 |
|
|
|
[43] |
1973 |
1000 |
1000 |
1.0 |
1 |
-3 |
√ |
[44] |
1974 |
|
600 |
|
|
|
|
[45] |
1974 |
|
2450 |
|
|
|
|
[45] |
1975 |
|
148 |
|
|
|
|
[46] |
1975 |
|
800 |
|
0.28 |
-2.54 |
|
[47] |
1975 |
|
1490 |
|
|
|
|
[46] |
1975 |
50 |
|
|
|
|
|
[48] |
1977 |
15 |
|
|
|
|
|
[49] |
1979 |
30 |
|
|
|
|
|
[50] |
1980 |
|
15 |
|
|
|
|
[26] |
1980 |
|
50 |
|
|
|
|
[26] |
1980 |
|
100 |
|
|
|
|
[26] |
1980 |
40 |
50 |
1.25 |
|
|
√ |
[51] |
1980 |
1000 |
|
|
|
|
√ |
[52] |
1982 |
|
1000 |
|
2 |
-3.3 |
|
[53] |
1982 |
400 |
1000 |
2.5 |
2.03 |
-3.31 |
√ |
[54] |
1988 |
|
90 |
|
|
|
|
[13] |
1988 |
|
300 |
|
|
|
|
[55] |
1988 |
|
1000 |
|
|
|
|
[55] |
1989 |
|
1 |
|
|
|
|
[56] |
1989 |
40 |
5 |
|
0.125 |
-2.54 |
√ |
[57] |
1989 |
500 |
|
|
|
|
|
[58] |
1991 |
|
2480 |
|
|
|
|
[59] |
1991 |
|
9200 |
|
|
|
|
[59] |
1992 |
36 |
40 |
|
|
|
√ |
[60] |
1993 |
228 |
|
|
|
|
√ |
[61] |
1993 |
|
100 |
|
|
|
|
[62] |
1993 |
360 |
870 |
2.4 |
0.85 |
-2.99 |
√ |
[63] |
1993 |
|
900 |
|
|
|
|
[62] |
1993 |
3000 |
25 |
0.0083 |
0.05 |
-3.30 |
|
[64] |
1993 |
3000 |
25 |
0.0083 |
3 |
-5.08 |
|
[64] |
1995 |
|
100 |
|
|
|
|
[65] |
1995 |
|
200 |
|
|
|
|
[66] |
1995 |
|
500 |
|
|
|
|
[65] |
1995 |
|
1000 |
|
|
|
|
[66] |
1995 |
22 |
|
|
0.94 |
|
|
[67] |
1995 |
500 |
80 |
0.16 |
|
|
|
[68] |
1995 |
500 |
800 |
1.6 |
|
|
|
[68] |
1996 |
|
680 |
|
|
|
|
[69] |
1996 |
|
2610 |
|
|
|
|
[69] |
1996 |
1660 |
400 |
0.241 |
2.45 |
-3.79 |
√ |
[70] |
1997 |
|
1 |
|
|
|
|
[71] |
1997 |
|
60 |
|
|
|
|
[72] |
1998 |
|
10 |
|
|
|
|
[73] |
1998 |
22.5 |
500 |
22.2 |
1.240 |
-3.39 |
|
[74] |
1998 |
97 |
|
|
|
|
|
[75] |
1999 |
|
0.45 |
|
1 |
-6.35 |
|
[76] |
1999 |
7 |
300 |
42.9 |
50 |
-5.22 |
|
[77] |
1999 |
35 |
50.5 |
1.44 |
|
|
√ |
[78] |
2000 |
2.5 |
5 |
2.0 |
|
|
√ |
[79] |
2000 |
100 |
600 |
6 |
1.6 |
-3.43 |
√ |
[80] |
2001 |
6 |
|
|
|
|
√ |
[81] |
2002 |
2200 |
600 |
0.27 |
1.302 |
-3.34 |
√ |
[82] |
2003 |
0.030 |
150 |
5000 |
27 |
-5.26 |
|
[22] |
2003 |
50 |
5 |
0.1 |
|
-4.99 |
√ |
[83] |
2003 |
50 |
50 |
1.0 |
0.492 |
-3.99 |
√ |
[83] |
2004 |
|
100000 |
|
|
|
|
[84] |
2004 |
48.23 |
|
|
|
|
√ |
[85] |
2004 |
154 |
300 |
1.95 |
1.18 |
-3.59 |
√ |
[86] |
2004 |
154 |
1000 |
6.49 |
1.18 |
-3.07 |
√ |
[86] |
2005 |
127 |
|
|
|
|
|
[87] |
2006 |
12 |
|
|
|
|
√ |
[88] |
2006 |
50 |
30 |
0.6 |
0.32 |
-4.03 |
√ |
[89] |
2006 |
50 |
100 |
2.0 |
2 |
-4.30 |
|
[90] |
2006 |
100 |
100 |
1.0 |
2 |
-4.30 |
|
[90] |
2006 |
100 |
300 |
3.0 |
2 |
-3.82 |
|
[90] |
2006 |
100 |
600 |
6.0 |
2 |
-3.52 |
|
[90] |
2006 |
200 |
100 |
0.5 |
2 |
-4.30 |
|
[90] |
2006 |
200 |
300 |
1.5 |
2 |
-3.82 |
|
[90] |
2007 |
0.020 |
|
|
|
|
√ |
[23] |
2007 |
0.175 |
|
|
|
|
√ |
[91] |
2007 |
48 |
7 |
0.15 |
|
|
√ |
[92] |
2007 |
100 |
300 |
3.0 |
1.2 |
-3.60 |
√ |
[93] |
2007 |
100 |
1200 |
12.0 |
1.2 |
-3.00 |
√ |
[93] |
2007 |
194 |
400 |
2.1 |
0.8771 |
-3.34 |
√ |
[94] |
2007 |
194 |
600 |
3.09 |
1.00 |
-3.22 |
√ |
[95] |
2008 |
|
1.86 |
|
|
|
|
[96] |
2008 |
|
250000 |
|
|
|
|
[97] |
2008 |
0.15 |
0.3 |
2 |
0.16 |
-4.90 |
√ |
[98] |
2008 |
0.35 |
0.7 |
2 |
0.18 |
-4.95 |
√ |
[98] |
2008 |
0.8 |
5 |
6.25 |
0.2 |
-4.51 |
√ |
[98] |
2008 |
50 |
0.9 |
0.018 |
|
|
√ |
[99] |
2008 |
50 |
13.9 |
0.28 |
|
|
√ |
[99] |
2008 |
200 |
800 |
4.0 |
0.75 |
-2.97 |
|
[100] |
2008 |
380 |
10 |
0.026 |
0.6 |
-4.78 |
√ |
[101] |
2008 |
380 |
100 |
0.26 |
0.6 |
-3.78 |
√ |
[101] |
2009 |
47 |
|
|
|
|
√ |
[102] |
2010 |
|
100 |
|
|
|
|
[103] |
2010 |
0.13 |
0.05 |
0.38 |
|
|
|
[104] |
2010 |
0.15 |
2.3 |
15.3 |
|
|
|
[105] |
2010 |
5.5 |
|
|
|
|
|
[5] |
2010 |
20 |
|
|
|
|
|
[5] |
2010 |
23.6 |
140 |
5.9 |
|
|
|
[106] |
2010 |
23.6 |
690 |
29.0 |
|
|
|
[106] |
2011 |
100 |
|
|
|
|
√ |
[107] |
2011 |
2540 |
1000 |
0.394 |
1.45 |
-3.16 |
√ |
[108] |
2011 |
2540 |
20000 |
0.787 |
1.45 |
-1.86 |
√ |
[108] |
2012 |
|
40 |
|
|
|
|
[109] |
2012 |
0.074 |
|
|
|
|
√ |
[110] |
2012 |
22 |
300 |
13.6 |
|
|
√ |
[111] |
2012 |
22 |
800 |
36.4 |
|
|
√ |
[111] |
2012 |
70 |
600 |
8.57 |
0.7 |
-3.07 |
√ |
[112] |
2013 |
|
100 |
|
|
|
|
[113] |
2013 |
|
7000 |
|
|
|
|
[114] |
2013 |
50 |
|
|
|
|
√ |
[115] |
2013 |
100 |
|
|
|
|
√ |
[115] |
2013 |
154 |
400 |
2.6 |
|
|
√ |
[116] |
2013 |
2540 |
|
|
0.64 |
|
√ |
[117] |
2013 |
2540 |
|
|
1.45 |
|
√ |
[118] |
2014 |
|
600 |
|
|
|
√ |
[119] |
2014 |
|
6000 |
|
|
|
|
[120] |
2014 |
5 |
55 |
11 |
|
|
√ |
[121] |
2014 |
8 |
|
|
|
|
|
[122] |
2014 |
12.1 |
|
|
|
|
√ |
[123] |
2014 |
127 |
260 |
0.205 |
0.10 |
-2.58 |
√ |
[124] |
2014 |
127 |
260 |
0.205 |
0.25 |
-2.98 |
√ |
[124] |
2014 |
600 |
55 |
0.092 |
|
|
√ |
[121] |
2014 |
1300 |
500 |
0.38 |
1.1 |
-3.34 |
√ |
[125] |
2014 |
1300 |
5000 |
3.8 |
1.1 |
-2.34 |
√ |
[125] |
2014 |
1500 |
|
|
|
|
√ |
[126] |
2015 |
|
55 |
|
|
|
|
[127] |
2015 |
|
400 |
|
|
|
|
[128] |
2015 |
|
5500 |
|
|
|
|
[128] |
2015 |
33 |
500 |
15 |
0.84 |
-3.23 |
√ |
[129] |
2015 |
55 |
30 |
0.55 |
0.14 |
-3.67 |
√ |
[130, 131] |
2015 |
55 |
30 |
0.55 |
0.24 |
-3.90 |
√ |
[130, 131] |
2016 |
|
200 |
|
|
|
|
[132] |
2016 |
|
400 |
|
|
|
|
[133] |
2016 |
|
7000 |
|
|
|
|
[132] |
2016 |
|
8000 |
|
|
|
|
[134] |
2016 |
|
8000 |
|
|
|
|
[135] |
2016 |
|
8000 |
|
|
|
|
[136] |
2016 |
|
600000 |
|
|
|
|
[137] |
2016 |
0.015 |
|
|
|
|
√ |
[138] |
2016 |
4.3 |
|
|
|
|
√ |
[139] |
2016 |
8.75 |
|
|
|
|
√ |
[140] |
2016 |
8.75 |
5 |
0.57 |
|
|
√ |
[141, 142] |
2016 |
10 |
400 |
40.0 |
1.000 |
-3.40 |
√ |
[143] |
2016 |
10 |
1000 |
100.0 |
1.000 |
-3.00 |
√ |
[143] |
2016 |
46 |
24 |
0.52 |
143 |
-6.78 |
√ |
[144] |
2016 |
50 |
100 |
2.0 |
0.2617 |
-3.42 |
√ |
[145] |
2016 |
75 |
|
|
|
|
|
[146] |
2016 |
75 |
5 |
0.067 |
|
|
|
[147] |
2016 |
127 |
5 |
0.039 |
0.265 |
-4.72 |
√ |
[148] |
2016 |
172 |
5 |
0.029 |
|
|
|
[147] |
2016 |
194 |
|
|
|
|
√ |
[149] |
2016 |
200 |
1 |
0.005 |
1.23 |
-6.09 |
√ |
[150] |
2016 |
200 |
5 |
0.025 |
1.23 |
-5.39 |
√ |
[150] |
2016 |
450 |
|
|
|
|
√ |
[151] |
2016 |
1000 |
400 |
0.40 |
1.000 |
-3.40 |
√ |
[143] |
2016 |
1000 |
1000 |
1.0 |
1.000 |
-3.00 |
√ |
[143] |
Traditionally, CT algorithms treat the focal spot x-ray source as if it were a single mathematical point[152], despite the fact that the finite focal spot width is known to limit the resolution of CT[4, 153, 154]. Our FoxelCT algorithm accounts for the focal spot as an extended source.
To this day (and earlier[155]), progress in reducing focal spot sizes has been hampered by the proportionality of x-ray flux to focal spot size[156] (Figure 2, Table 2):
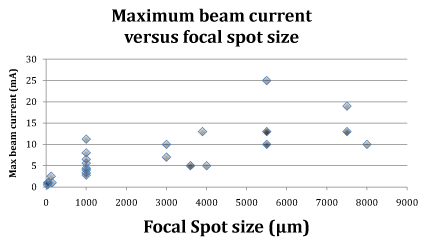
Figure 2. Maximum beam current in mA versus maximum dimension of the focal spot size f (µm) for some contemporary rotating anode x-ray tubes (listed in Table 2). Note that there is an approximate proportionality consistent with the prediction of[156] for small focal spot sizes and with the correspondence between electron spot size and focal spot size[157]. Part of the scatter here may be due to the fact that we are using the largest linear dimension rather than the area of the focal spot.
Table 2. Manufacturers’ specifications for some contemporary rotating anode x-ray tubes.
Company/Model |
Maximum focal spot
width (µm) |
Maximum beam current (mA) |
Source |
Gulmay |
|
|
[135] |
NDI 320/23 |
3600 |
5 |
|
NDI 322 |
4500 |
10 |
|
NDI 320/26 |
5500 |
13 |
|
NDI 321 |
8000 |
12.5 |
|
Oxford Instruments |
|
|
[158] |
1000 Series - 90507 Glass X-ray Tube |
33 |
0.5 |
|
Jupiter 5000 Series Radiation Shielded X-ray Tube |
55 |
1.0 |
|
1501 Series Glass X-ray Tube |
125 |
2.5 |
|
1500 Series Glass X-ray Tube |
150 |
1.0 |
|
Varian |
|
|
[159] |
NDI-225/20 |
1000 |
2.8 |
|
HPX-450/11 |
1000 |
3.3 |
|
NDI-160/20 |
1000 |
4 |
|
HPX-225/20 |
1000 |
4.4 |
|
HPX-320/11 |
1000 |
5.6 |
|
HPX-160/20 |
1000 |
6.5 |
|
HPX-225/11 |
1000 |
8 |
|
HPX-160/11 |
1000 |
11.25 |
|
NDI-225/21 |
3000 |
7 |
|
NDI-160/21 |
3000 |
10 |
|
NDI-320/23 |
3600 |
5 |
|
NDI-350/23 |
3600 |
5 |
|
HPC-225FB |
3900 |
13 |
|
NDI-350/26 |
4000 |
5 |
|
NDI-451 |
5500 |
10 |
|
NDI-452 |
5500 |
10 |
|
NDI-160/22 |
5500 |
13 |
|
NDI-225/22 |
5500 |
13 |
|
NDI-320/26 |
5500 |
13 |
|
HPC-160FB |
5500 |
25 |
|
NDI-225FB |
7500 |
13 |
|
NDI-226 |
7500 |
13 |
|
NDI-161 |
7500 |
19 |
|
NDI-321 |
8000 |
10 |
|
“The tube power basically influences two different image quality criteria. On the one hand, the focal spot size is limiting the spatial resolution and is supposed to be more enlarged for higher tube powers. On the other hand, sufficient radiation intensities are necessary to achieve adequate signal-to-noise ratios. These two image quality criteria, which are contrarily related to the tube power, need to be well balanced in a sample specific way”[123].
“The main trade-offs in x-ray tube design are the total x-ray photon output and the size of the region of x-ray generation/electron beam footprint on the anode or target (also named thermal focal spot). More photons can be created by increasing the electron beam power, but this is limited by target melting and/or rapid evaporation, and/or lifetime degradation due to thermal cycling. One could prevent target melting by increasing the thermal focal spot size; however, this may cause a larger optical focal spot with consequences in degraded image resolution…. In an ideal system, the origin of the x-ray flux is treated as a point source to maximize spatial resolution. In reality, this region must have a finite area to decrease the maximum heat flux on the target/anode for x-ray generation”[4].
“…technical measures to limit [CT] focal spot blooming are important to avoid reduced spatial resolution”[154].
Even in micro-CT: “The focal spot size of the x-ray tube varies from 5 µm to 30 µm depending on its output power …”[148].
Thus, while smaller focal spots have been achieved for various applications (Figure 3), they do not find much use in clinical CT because of reduced flux and high temperatures[160]. Nor are the larger focal spots (Figure 1) used in CT, because, treated as point sources, they would reduce image detail. While someday the standard medical x-ray rotating anode tube may be replaced by x-ray microbeams[161-163] or other technology, or the focal spot size made irrelevant via microcapillary[164-166], zone plate[167] or mirror[71] x-ray optics, in the interim we offer a partial solution to the dilemma via a new CT algorithm using foxels, which allows larger focal spots and/or smaller detector pixels to be considered.
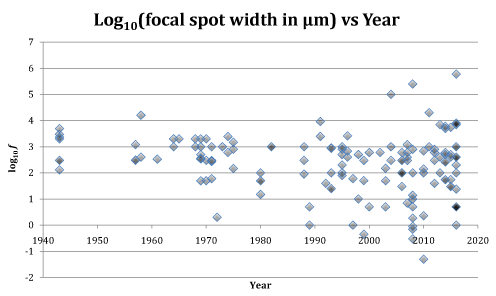
Figure 3. Logarithm of focal spot size in µm versus year. While there is a trend to quite small focal spots led by microtomography and nanotomography, in recent years extended area x-ray sources have also come into use, albeit for sterilization of large volumes rather than for imaging. Thus, we also have a trend to large focal spots. See Table 1.
In standard projection radiography, the loss of detail with large focal spots may sometimes be diagnostically acceptable:
“This investigation demonstrates that the impact of focal spot size choice for a number of examination types is limited, and there appears to be little support for using fine focus for at least some projections where it would have traditionally been employed. Whilst the authors at this preliminary stage do not propose that multi-foci X-ray tubes have no future role in radiology departments, the advantages of a single broad focus X-ray tube in terms of lower manufacturing costs, reduced customer service and replacement expenses and the ability to set shorter times to minimize movement unsharpness cannot be dismissed”[168].
“The results of this study suggest that the clinical significance of varied focal spot size is negligible”[69].
With the use of foxels, one may keep all of these advantages of large focal spots while attaining much of the advantage of small focal spots, a form of nearly “having one’s cake and eating it too”. The perception that we need small x-ray focal spots has been legislated, at least for mammography[169], though foxels could render this legal approach to x-ray physics moot.
One would think that a rational approach would be to at least match the detector width to the focal spot width, but this does not seem to be happening (Figure 4). Nor have we found any literature that addresses optimizing this ratio. Another important ratio is the focal spot width to the gantry diameter. This ratio is widely scattered and skewed towards low values (Figure 5), whereas the use of foxels would suggest that higher values are attainable. Therefore our simulated experiments here delve into a range of CT parameters whose optimization is usually not considered.
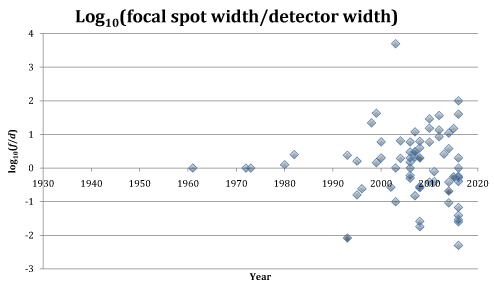
Figure 4. Ratio of focal spot width f to detector pixel width d versus year. The scale is dimensionless, since both are measured in µm. In recent years the ratio of the focal spot width to the detector width has had two opposite trends, both increasing and decreasing, but with everything in between. For those systems with an increased ratio, resolution could be improved using foxels, if the distance between focal spot and detector isn’t too large (see Figure 5). Data from Table 1.
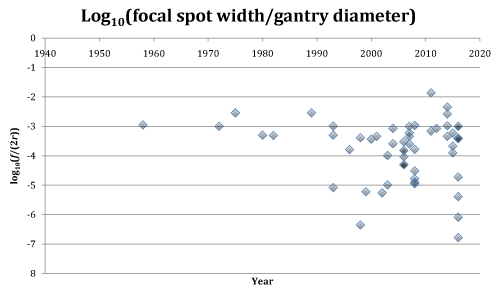
Figure 5. Logarithm of the dimensionless ratio of focal spot width f to gantry diameter 2r versus year, which we take as being the distance between the focal spot and the detector pixels. With finer focal spots, especially in synchrotron nanotomography, the ratio of focal spot width to gantry diameter has been plunging in recent years. Here we argue that, with the use of foxels, it should be substantially increased. Data from Table 1.
The finite width of the focal spot has been invoked to reduce the resolution of simulated CT to make the latter more “realistic”[170]. Here we take the opposite approach and make use of the width of the focal spot to increase resolution (Figure 6).
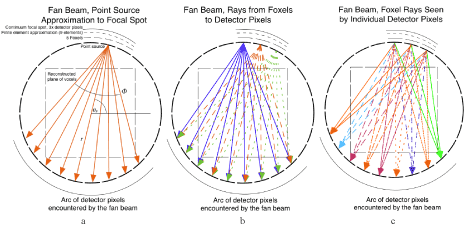
Figure 6. Conventional CT versus FoxelCT. (a): A conventional fan-beam CT scan algorithm treats the focal spot as if it were a single point from which rays are projected to the detector pixels. The square is the region being reconstructed, represented digitally by array U, whose iterative approximations are the arrays Ai. The arcs on top indicate: 1) solid line, the focal spot as a continuum x-ray emitter, in this case of width (arc length) fw equal to that of 3 detector pixels of width d (i.e., fw = 3d); 2) small dashes, the continuum focal spot approximated by 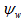 finite elements; 3) large dashes, aw = 5 foxels used in reconstructing the plane of voxels. aw is an independent variable. In our simulation, these three arcs would be superimposed on the ring of detector pixels. They are displaced radially here for clarity. (b): The focal spot is divided into multiple foxels (just aw = 3 here) which project rays onto the detector pixels. For aw = 3 here, the foxels have the same width as the detector pixels. The projections are taken from the midpoints of the foxels. The rays from each foxel are colored differently. Dashes are to make the figure understandable in gray scale. (c): The same rays are recolored according to which detector pixels see them. For each detector pixel, these are the rays, grouped into a compound ray, used to calculate
finite elements; 3) large dashes, aw = 5 foxels used in reconstructing the plane of voxels. aw is an independent variable. In our simulation, these three arcs would be superimposed on the ring of detector pixels. They are displaced radially here for clarity. (b): The focal spot is divided into multiple foxels (just aw = 3 here) which project rays onto the detector pixels. For aw = 3 here, the foxels have the same width as the detector pixels. The projections are taken from the midpoints of the foxels. The rays from each foxel are colored differently. Dashes are to make the figure understandable in gray scale. (c): The same rays are recolored according to which detector pixels see them. For each detector pixel, these are the rays, grouped into a compound ray, used to calculate 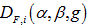 in Equation 2. A similar calculation, emanating from the
in Equation 2. A similar calculation, emanating from the 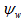 finite elements, is used to calculate the forward projection data
finite elements, is used to calculate the forward projection data 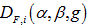 in Equation 1 for the same detector pixels. Note that the use of foxels does not change the gantry configuration at all. It just allows the focal spot to be represented more realistically as having some width. In relation to our equations, the gantry angle
in Equation 1 for the same detector pixels. Note that the use of foxels does not change the gantry configuration at all. It just allows the focal spot to be represented more realistically as having some width. In relation to our equations, the gantry angle 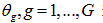 is the angle of the line between the middle of the focal spot and the detector pixel in the middle of the arc of detector pixels encountered by the fan beam of angle
is the angle of the line between the middle of the focal spot and the detector pixel in the middle of the arc of detector pixels encountered by the fan beam of angle 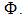 . The length of that line is the diameter 2r of the gantry. This geometry can represent either a third generation CT scanner, in which the arc of detector pixels and the x-ray source rotate together, or a fourth-generation scanner, in which there is a full ring of stationary detector pixels, and only the x-ray source rotates. However, we do constrain both to have equal distances r from the center of rotation in our simulation. The indexing of the detector pixels in the fan beam, a = 1,....amax , depends on which generation scanner is being considered. The index β is needed when the detector array is two dimensional. Our code applies to third generation, though our results are independent of third versus fourth generation. Note that figures similar to (b) and (c) could be drawn for the finite elements, but would involve different rays between the finite elements and the detector pixels
. The length of that line is the diameter 2r of the gantry. This geometry can represent either a third generation CT scanner, in which the arc of detector pixels and the x-ray source rotate together, or a fourth-generation scanner, in which there is a full ring of stationary detector pixels, and only the x-ray source rotates. However, we do constrain both to have equal distances r from the center of rotation in our simulation. The indexing of the detector pixels in the fan beam, a = 1,....amax , depends on which generation scanner is being considered. The index β is needed when the detector array is two dimensional. Our code applies to third generation, though our results are independent of third versus fourth generation. Note that figures similar to (b) and (c) could be drawn for the finite elements, but would involve different rays between the finite elements and the detector pixels
Foxels were independently proposed by us[2, 7, 171] and at about the same time by other groups, who called them “subfocal spots”[172] and “source-lets”[94]. They offer a real space approach to deconvolution of the focal spot[173-176] with the attendant flexibility of iterative algorithms, without making any approximations[177, 178] to the usually complex structure of a focal spot (Figure 7). The area integral model (AIM) uses double integrals to estimate absorption between an extended focal spot and an extended detector pixel[179]. These double integrals are special cases of the general notion of a “passage” between the x-ray source and detector[180] or “ray sum”[181], also known as “a finite beamwidth”[182, 183]. Ray modelling (RM)[125, 184] is equivalent to foxel imaging, with the addition of division of the (1.3 mm, in their case) detector pixels and incorporation of photon noise. A similar approach uses an “eleven-fold subsampling of the [focal] spot area” and “pixels (sub-detectors) covering the detector area”[185]. “High fidelity modeling” includes a focal spot model and a detector response function[186]. An ART-like algorithm has been used to estimate projection data for an ideal point source from projection data for an extended focal spot, and then reconstruct images assuming a point source[187].

Figure 7. Focal spots with a variety of shapes. Note that in the digitized focal spot images each pixel could be regarded as a foxel, since in a real situation 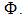 is measured, and need not be calculated from finite elements. (a): Gray scale reversal of a focal spot from[188] with kind permission of Sanja Valentic. (b): From[189] with kind permission of Medical Physics and author John M. Boone. Width is 300 µm. (c): “Isopower (640W) focal spot images (1 mm, EN12543) depicting considerably lower surface temperatures for an HP [high power] technology anode [right; versus conventional anode: left].” From[133] with kind permission of Jim Kone. (d): Nearly symmetric focal spot of a carbon nanotube x-ray source. From[112] with kind permission of Medical Physics and author Otto Zhou. (e): Focal spot scanned from mammographic film. From[94] with kind permission of Medical Physics and author John M. Boone. (f,g): Focal spots from the same CT scanner at its maximum amperage for 70 kV and 120 kV. From[154] with kind permission of Medical Physics and author Cynthia H. McCollough. For a mammography focal spot that is highly structured see[47]. For efforts to reduce that structure see[190]. The space charge of electrons[21, 154], magnetic fields[100, 191, 192], as in dual CT/MRI scanners, and position along the cathode/anode axis[193] and projection direction[194, 195], all alter the size and shape of focal spots. While we are assuming that the focal spot does not vary in the course of data collection for a single image, we found no proof of this in the literature. Given the variability in the shape of the focal spot with amperage and voltage[154] and the little explored variation over long time[196], mechanical movement[183, 197] and vibration[98] and other effects requiring physical or algorithmic realignment[198], it would be wise to have a built in, periodic, automatic, digital imaging of the focal spot, its spatial variation, and its position[199] in CT scanners using the FoxelCT algorithm.
is measured, and need not be calculated from finite elements. (a): Gray scale reversal of a focal spot from[188] with kind permission of Sanja Valentic. (b): From[189] with kind permission of Medical Physics and author John M. Boone. Width is 300 µm. (c): “Isopower (640W) focal spot images (1 mm, EN12543) depicting considerably lower surface temperatures for an HP [high power] technology anode [right; versus conventional anode: left].” From[133] with kind permission of Jim Kone. (d): Nearly symmetric focal spot of a carbon nanotube x-ray source. From[112] with kind permission of Medical Physics and author Otto Zhou. (e): Focal spot scanned from mammographic film. From[94] with kind permission of Medical Physics and author John M. Boone. (f,g): Focal spots from the same CT scanner at its maximum amperage for 70 kV and 120 kV. From[154] with kind permission of Medical Physics and author Cynthia H. McCollough. For a mammography focal spot that is highly structured see[47]. For efforts to reduce that structure see[190]. The space charge of electrons[21, 154], magnetic fields[100, 191, 192], as in dual CT/MRI scanners, and position along the cathode/anode axis[193] and projection direction[194, 195], all alter the size and shape of focal spots. While we are assuming that the focal spot does not vary in the course of data collection for a single image, we found no proof of this in the literature. Given the variability in the shape of the focal spot with amperage and voltage[154] and the little explored variation over long time[196], mechanical movement[183, 197] and vibration[98] and other effects requiring physical or algorithmic realignment[198], it would be wise to have a built in, periodic, automatic, digital imaging of the focal spot, its spatial variation, and its position[199] in CT scanners using the FoxelCT algorithm.
Another approach, shown to be noise sensitive, is to deblur the focal spot by Fourier space/Wiener deconvolution methods[178, 200]. However, it is important to take into account the varying effects of the focal spot on voxels at different distances from the x-ray source. While the trapezoidal “footprint” or shadow of each voxel being reconstructed can be calculated[201], rotation of the voxels so they cast a rectangular footprint in each projection direction has been found to improve the image[202]. This notion of a manipulable voxel is related to pointillism[2]. Focal spots have been divided into many “segments” where “each segment carries a certain intensity weight” for a ray tracing analysis of the effects of focal spot shape on resolution[203], but this was not used for deconvolution. X-ray capillary optics[204] may be looked upon as directly segmenting and measuring the focal spot rays down to as little as[205] 1 µm. Unless a light field optics approach is taken, x-ray capillary optics might not work well with large focal spots[166], because the angular acceptance of each microcapillary tube is small, leading to trade-offs in angle coverage, flux and dose to the patient.
Our purpose here is to put an upper bound on the improvement that foxels can bring, and to optimize that improvement with respect to two parameters: the ratio of focal spot width 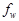 to detector pixel width d and the number of foxels into which the focal spot is partitioned. To do this we simulate a fixed gantry diameter (distance of focal spot to the detector pixel at the center of the fan beam) of 2r = 870 mm, using a fan beam geometry with fan angle
to detector pixel width d and the number of foxels into which the focal spot is partitioned. To do this we simulate a fixed gantry diameter (distance of focal spot to the detector pixel at the center of the fan beam) of 2r = 870 mm, using a fan beam geometry with fan angle 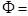 57o (Figure 8, Table 3), with αmax = 865 detector pixels inside the fan beam, and ignore photon and instrument noise, heel effect[206, 207], beam hardening, etc., in this, our initially strictly geometric approach to this problem. While all of those parameters would degrade the reconstructed images, the geometric approach is valuable in giving an upper bound on what is achievable. We leave the effects on foxel CT of noise, etc., for future work. We find that foxels can offer an alternative to microfocal spot systems, retaining much of their high resolution while allowing the high flux of broad x-ray sources. Even though we have concentrated on CT, foxels are equally applicable to ordinary projection radiography, digital versions of classical tomography, and tomosynthesis. The goal of foxel based computed tomography (FoxelCT) is to try to achieve a spatial resolution limited by the detector pixel size rather than the focal spot size. The advantage to the patient is higher resolution for a given x-ray dose, lower dose for the same resolution, or shorter exposure times, reducing patient motion, heart motion, etc.
57o (Figure 8, Table 3), with αmax = 865 detector pixels inside the fan beam, and ignore photon and instrument noise, heel effect[206, 207], beam hardening, etc., in this, our initially strictly geometric approach to this problem. While all of those parameters would degrade the reconstructed images, the geometric approach is valuable in giving an upper bound on what is achievable. We leave the effects on foxel CT of noise, etc., for future work. We find that foxels can offer an alternative to microfocal spot systems, retaining much of their high resolution while allowing the high flux of broad x-ray sources. Even though we have concentrated on CT, foxels are equally applicable to ordinary projection radiography, digital versions of classical tomography, and tomosynthesis. The goal of foxel based computed tomography (FoxelCT) is to try to achieve a spatial resolution limited by the detector pixel size rather than the focal spot size. The advantage to the patient is higher resolution for a given x-ray dose, lower dose for the same resolution, or shorter exposure times, reducing patient motion, heart motion, etc.
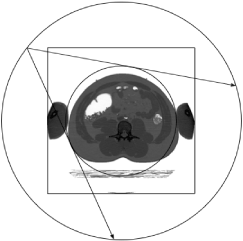
Figure 8. Simulation parameters drawn to scale. Based on the parameters of contemporary body scanners (Table 3), we have chosen to simulate a gantry of diameter 2r = 870 mm with a fan beam angle of 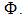 subtending 865 detector pixels. The full ring, in fourth generation CT configuration, would have 2733 detector pixels. The detector pixels are 1 mm wide, as are the 512 x 512 voxels in the slice. A bow tie filter[208] is not simulated. Note that at some gantry angles the fan beam does not include the whole cross section of this 199 lb = 90.3 kg Visible Human Male[209], which has been gray scale reversed here so that “air” (see Figure 9) shows as white. The inner circle shows which voxels are included in the fan beam at all angles. It is sometimes apparent in individual reconstructed images.
subtending 865 detector pixels. The full ring, in fourth generation CT configuration, would have 2733 detector pixels. The detector pixels are 1 mm wide, as are the 512 x 512 voxels in the slice. A bow tie filter[208] is not simulated. Note that at some gantry angles the fan beam does not include the whole cross section of this 199 lb = 90.3 kg Visible Human Male[209], which has been gray scale reversed here so that “air” (see Figure 9) shows as white. The inner circle shows which voxels are included in the fan beam at all angles. It is sometimes apparent in individual reconstructed images.
Table 3. Contemporary CT body scanners. Data from[212]. We assume that the reported “Elements per row” = “# of detector pixels hit by fan beam”, that the gantry diameter is the distance between the x-ray focal spot and the detector pixels, and that both the minimum and maximum focal spot sizes are parallel to a section. Parameters calculated from the data are indicated by *. In calculating the section widths of the detector elements we are assuming that the detectors and the x-ray focal spot are the same distance from the center of rotation. While this assumption may not be exact for the individual scanners listed here, it is a special case of both third and fourth generation CT scanners[213, 214] (Figure 6). The last row shows the values we chose for the simulations in this paper. We have selected the largest fan beam angle 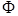 represented by these commercial whole body scanners, the smallest gantry diameter, and a detector pixel width that matches the voxel width in the CT scans of the Visual Human Male[209], which we take as 1 mm. We consider focal spot widths
represented by these commercial whole body scanners, the smallest gantry diameter, and a detector pixel width that matches the voxel width in the CT scans of the Visual Human Male[209], which we take as 1 mm. We consider focal spot widths 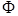 from zero (the point source simulation) to 21 mm, a range that includes most standard x-ray sources used for radiography, and is more than twice as big as the larger focal spot sizes we found for a rotating anode x-ray tube (8 mm in[134-136] and an estimated 9.2 mm in[59]) (Table 1). Our work therefore could extend the narrow range of focal spot sizes used in contemporary CT scanners, 0.5 to 1.6 mm in this table, by an order of magnitude.
from zero (the point source simulation) to 21 mm, a range that includes most standard x-ray sources used for radiography, and is more than twice as big as the larger focal spot sizes we found for a rotating anode x-ray tube (8 mm in[134-136] and an estimated 9.2 mm in[59]) (Table 1). Our work therefore could extend the narrow range of focal spot sizes used in contemporary CT scanners, 0.5 to 1.6 mm in this table, by an order of magnitude.
Company / Model |
Year |
# rows of
detectors |
Width of detector
block (mm) |
*z-width ofdetector
pixels (mm) |
# of detector pixels
hit by fanbeam |
Fan beam
angle (degrees) |
Gantry diameter
(2r, mm) |
*Section width
d of detector
elements (mm) |
Smallest focal
spot width (mm) |
Largest focal
spot width (mm) |
*log10 (largest focal
spot width/
gantry diameter) |
Hitachi |
|
|
|
|
|
|
|
|
|
|
|
Supria 16 |
2014 |
32 |
20 |
0.625 |
880 |
51.78 |
920 |
0.472 |
0.7 |
1.4 |
-2.82 |
Scenaria 64 |
2010 |
64 |
40 |
0.635 |
888 |
51.78 |
880 |
0.448 |
0.7 |
1.4 |
-2.80 |
Scenaria Advanced 128 |
2011 |
64 |
40 |
0.625 |
888 |
51.78 |
880 |
0.448 |
0.7 |
1.4 |
-2.80 |
Neusoft |
|
|
|
|
|
|
|
|
|
|
|
NeuViz 16 |
2008 |
16 |
24 |
1.5 |
672 |
52 |
890 |
0.601 |
0.5 |
1.3 |
-2.84 |
NeViz64i |
2012 |
64 |
20 |
0.3125 |
672 |
52 |
890 |
0.601 |
0.6 |
1.2 |
-2.87 |
NeuViz 64c Cardiac (Basic) |
2012 |
64 |
20 |
0.3125 |
672 |
52 |
890 |
0.601 |
0.6 |
1.2 |
-2.87 |
Philips |
|
|
|
|
|
|
|
|
|
|
|
IQon Spectral CT |
2015 |
128 |
40 |
0.3125 |
1344 |
52 |
970 |
0.328 |
0.6 |
1.2 |
-2.91 |
iCT Elite |
2015 |
128 |
80 |
0.625 |
672 |
52 |
970 |
0.655 |
0.6 |
1.2 |
-2.91 |
iCT SP |
2015 |
64 |
40 |
0.625 |
672 |
52 |
970 |
0.655 |
0.6 |
1.2 |
-2.91 |
Ingenuity Elite |
2015 |
64 |
40 |
0.625 |
672 |
54 |
940 |
0.659 |
0.5 |
1.0 |
-2.97 |
Ingenuity Core |
2015 |
64 |
40 |
0.625 |
672 |
54 |
940 |
0.659 |
0.5 |
1.0 |
-2.97 |
Ingenuity Flex32 |
2015 |
16 |
24 |
1.5 |
672 |
57 |
940 |
0.696 |
0.5 |
1.0 |
-2.97 |
Ingenuity Flex |
2015 |
16 |
24 |
1.5 |
672 |
57 |
940 |
0.696 |
0.5 |
1.0 |
-2.97 |
Brilliance CT Big Bore |
2015 |
16 |
24 |
1.5 |
816 |
57 |
970 |
0.591 |
0.5 |
1.0 |
-2.97 |
MX 16EVO2 |
2015 |
16 |
24 |
1.5 |
672 |
57 |
890 |
0.659 |
0.5 |
1.3 |
-2.84 |
Toshiba |
|
|
|
|
|
|
|
|
|
|
|
AQ One Family |
2015 |
160 |
160 |
1.0 |
896 |
49.2 |
1070 |
0.513 |
0.8 |
1.6 |
-2.83 |
AQ Prime Series |
2015 |
40 |
40 |
1.0 |
896 |
49.2 |
870 |
0.417 |
0.8 |
1.6 |
-2.74 |
AQ RXL |
2011 |
32 |
32 |
1.0 |
896 |
49.2 |
960 |
0.460 |
0.8 |
1.6 |
-2.78 |
Simu-
lation |
2016 |
1 |
1 or 3 |
1 or 3 |
433 |
57.03 |
870 |
1.0 |
0 |
21 |
-1.62 |
Choice of CT algorithm
We use the MART algorithm (Multiplicative Algebraic Reconstruction Technique)[2, 180, 181, 215] which is a well characterized[216-225] nonlinear (non-Kaczmarz[2, 226]) iterative algorithm, not the best possible, but a good standard for comparison. Two desirable characteristics are: a) if MART is started from nonnegative voxel values, all voxels remain nonnegative as the calculation proceeds; b) where the x-rays have only traversed air, MART generates zero values for those voxels, and thus confines the reconstruction of the data to remain within the convex hull[221, 227-230] of the body. Improvements of MART that could be invoked include streak suppression[231, 232], metal artefact reduction[233], and postprocessing steps such as deconvolution of the point spread function of MART by Wiener filtration[234] and searches in the space of solutions of CT underdetermined equations[235].
Modeling an x-ray source with its focal spot width divided into finite elements
Although we will confine our computations in this introductory paper to 2D simulations of foxels, we will here develop the mathematics for the full 3D case for later use, and then derive 2D as a special case. For a given object or patient being scanned by the CT machine, let its voxels in 3D space be defined as U (x, y, z), where x, y, and z are the 3D coordinates of the center of each voxel (Figure 6 and Figure 8). As foxels represent a change in the geometry of rays rather than the physics of CT, at this point in their development we presume that U is a scalar function independent of time (no patient motion), that Beer’s Law holds (i.e., monochromatic x-rays), and do not consider calibration, beam hardening and scatter corrections, nor fluctuations in number of photons emitted, absorbed, or detected, i.e., noise [183, 236]. This allows us to focus on the question of whether or not the geometry of foxels by itself improves CT resolution. The results will then be an upper bound to the improvement in resolution using foxels. We plan to broach these effects, including full 3D CT, in subsequent papers in this series, to estimate lower bounds.
Let each voxel coordinate of U (x, y, z), be defined as an integer number from (1,1,1) to (xmax, ymax, zmax), with the voxels on a cubic grid with spacing 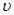 . This coordinate system is in the patient, and the gantry system containing x-ray sources and detectors is presumed to move relative to a stationary patient. For a gantry in which the patient is on a movable bed, the z-coordinate is along the bed, but in our coordinate system the bed is presumed stationary and the gantry moves. The difference can be made up via standard translation and rotation matrix transformations via homogeneous coordinates[237]. For 2D simulations z is taken as having a fixed value.
. This coordinate system is in the patient, and the gantry system containing x-ray sources and detectors is presumed to move relative to a stationary patient. For a gantry in which the patient is on a movable bed, the z-coordinate is along the bed, but in our coordinate system the bed is presumed stationary and the gantry moves. The difference can be made up via standard translation and rotation matrix transformations via homogeneous coordinates[237]. For 2D simulations z is taken as having a fixed value.
We will assume that the gantry itself has a known relationship between its extended 2D x-ray source S and its 2D array of detectors, and that the physical properties of the source are known and independent of time. Note that this definition of S includes the possibility of multiple simultaneous x-ray sources[4], each of which would have its own focal spot. Thus, while we speak here of a single focal spot, the mathematics allows multiple focal spots.
We will also assume that the gantry takes on G discrete positions or configurations, i.e., that there is no motion during acquisition of a given projection g, g=1,…..,G. This will accommodate classical and inverse-geometry CT systems[238, 239], including those with multiple detector arrays and source arrays[240]. Gantries that move during projection data acquisition, causing motion blurring of the data[241], would require a more detailed treatment.
The reading at each detector pixel will be DE (α, β, g) indexed by α = 1…..,αmax, β = 1,…βmax, g=1,…,G. Since the detector pixels generally correspond to physical detector elements, this array is not an approximation. However, we will take a DE value to be an integral over its detector element, while approximating its location by the center of the detector element. We will assume that the average distance between nearest neighbour detector pixels is the constant d. The arrangement of the detector elements is otherwise not restricted, allowing planar, cylindrical or spherical geometries of the detector array, for instance.
Physically the focal spot is a continuous function, so its digital representation as an emitting image needs to be defined. Focal spots can be quite irregular in shape (Figure 7). For convenience, we will assume that the focal spot S (u, v, K, µ) ≥ 0, where (u, v) is a coordinate system with the center of the focal spot at (u, v) = (0,0), and that it is contained within a rectangle chosen to have sides that are parallel to the grid directions of a rectangular detector array. The coordinates (u, v) can represent any 2D manifold, such as the curvature of a rotating anode, which is opposite the curvature depicted in Figure 6. The angular coordinates (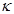 , µ) take into account that the intensity of the x-ray emission is angle dependent. This is the angular component of the heel effect, which also includes alteration of the x-ray spectrum [242], which we ignore for now, as we are focussing on geometric effects. Even without a heel effect, each detector pixel “sees” the focal spot rectangle from a different angle[120], and since this is a geometric effect, we take it into account in the general case.
, µ) take into account that the intensity of the x-ray emission is angle dependent. This is the angular component of the heel effect, which also includes alteration of the x-ray spectrum [242], which we ignore for now, as we are focussing on geometric effects. Even without a heel effect, each detector pixel “sees” the focal spot rectangle from a different angle[120], and since this is a geometric effect, we take it into account in the general case.
The width fw and height fh of the rectangle containing the focal spot are chosen to be odd integer multiples of the detector pixel width d. Outside of this rectangle we assume no source of x-rays, i.e., S (u, v, K, µ) = 0. Since we are considering broad x-ray focal spots, we allow the rectangle to be curved in one (as in Figure 6) or both directions.
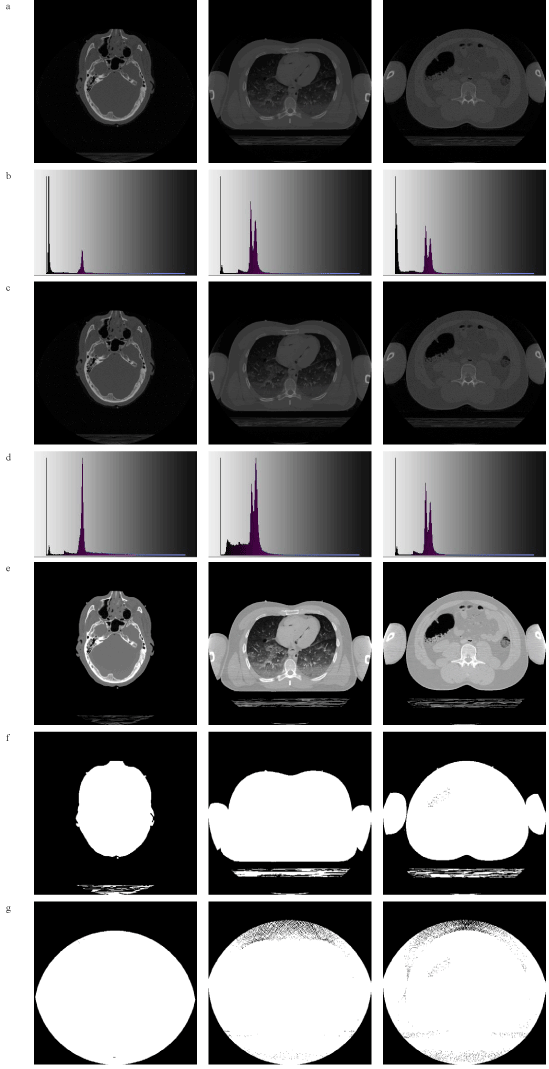
Figure 9. Visible Human Project samples. (a): Each image is a 512x512 pixel png file with 8-bit (0 to 255) gray values representing a slice of a CT scan of a human male taken before the cadaver was frozen and physically sliced[209]. Left column: A CT scan slice of the head, labelled in the Visible Human database as c_vm1125[210]. Surface bumps are cross sections of tubing containing a contrast solution. Center column: A thorax CT scan slice through the lungs, labelled c_vm1451. Right column: CT scan slice through the abdomen, labelled c_vm1671. The head slice thickness is 1 mm and the thorax and abdomen slices are 3 mm thick. Note that the standard radiology convention for viewing CT images is that the right side of the image corresponds to the patient’s left side, and vice versa. (b): Histograms of row (a). (c): The cadaver was embedded in an immobilizing foam, which we have here digitally removed around the body and table using the Compositor function Quickbrush[211], setting its pixel values to zero, to represent air. These images are used for the function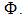 . (d): In the histograms of row (c) we now have a sharp air peak at 0 on the left. (e): A brightened version of the images in row (c), using the Autolevel function in Compositor, for the sake of making the anatomy more visible. (f): Bitmasks of row (c) showing air in black. (g): A bitmask consisting of the cadaver plus the immobilizing foam in white. The streaking artefact is from the CT scanner algorithm that was used to produce the images in the row (a).
. (d): In the histograms of row (c) we now have a sharp air peak at 0 on the left. (e): A brightened version of the images in row (c), using the Autolevel function in Compositor, for the sake of making the anatomy more visible. (f): Bitmasks of row (c) showing air in black. (g): A bitmask consisting of the cadaver plus the immobilizing foam in white. The streaking artefact is from the CT scanner algorithm that was used to produce the images in the row (a).
We use two different arrays to represent the continuum focal spot in our calculations: emission finite elements and foxels. Both are generally different digitization’s of the same function S (u, v, K, µ).
We designate the array of emission finite elements as E (ψ, ϕ, g), ψ = 1….ψw, ϕ = 1,…ϕh, , where g allows us to calculate the position of each emission finite element relative to the (x, y, z) coordinate system. The index g also implicitly includes the angle components of S (u, v, K, µ), and E (ψ, ϕ, g) is an integral over an appropriate patch of S (u, v, K, µ). The emission finite elements are used for the forward calculation, namely creating an estimate of the projection of U (x, y, z) onto the detector array. The centers of the finite elements are used for the calculation. We may refer to all of the line segments (rays) from all of the focal spot finite element centers to all of the detector element centers as the forward x-ray light field.
To represent the projection of finite element (ψ, ϕ, g) onto detector pixel DE (α, β, g) we use the function WE (α, β, ψ, ϕ, x, y, z, g). The function WE describe a weight between zero and one, which we base on a line between the centers of finite element (ψ, ϕ, g) and detector pixel (α, β, g). It includes the angular information in S (u, v, K, µ). The line weights WE are generated using the antialiasing Xiaolin Wu line algorithm[243] (Figure 10). Our use of the Wu algorithm, instead of the standard CT Mueller, Siddon and Joseph algorithms[244-246], provides a simple solution to the problem of assigning a weight to the intersection of a ray with a voxel[180]. A three-dimensional version is available[247].

Figure 10. Two rays drawn using the Wu antialiasing line drawing algorithm[243] and the user interface. (a): Left, two Wu rays. (b): On the right is a close-up showing the weights assigned to individual pixels along the rays.
Therefore, the measurements from which we reconstruct CT images are the set of all detector pixel readings:
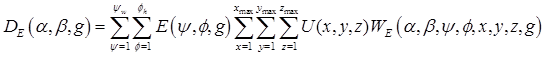 [1]
[1]
The subscript E on 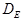 is a reminder that the finite elements are used in this calculation. Note that Equation 1 includes a sum over all finite element rays from the focal spot to the detector pixel, analogous to Figure 6c. These concatenated rays form a “compound ray”, an object that is no longer a simple line, but rather a bundle of lines. This conforms to our generalization of a ray as a “passage”, i.e., any weighted subset of voxels, no matter what its shape or position[180]. The use of compound rays removed the instabilities inherent in our previous approach[2, 7, 171], in which we attempted to estimate the ray sum for each individual subray from (ψ, ϕ, g) to detector pixel (α, β, g) in an algorithm we called SuperMART (Superresolution MART). Nevertheless, while FoxelCT directly calculates values for each voxel, it also, in effect, allows each subray to acquire its own subray sum. It thus also reconstructs the x-ray light field.
is a reminder that the finite elements are used in this calculation. Note that Equation 1 includes a sum over all finite element rays from the focal spot to the detector pixel, analogous to Figure 6c. These concatenated rays form a “compound ray”, an object that is no longer a simple line, but rather a bundle of lines. This conforms to our generalization of a ray as a “passage”, i.e., any weighted subset of voxels, no matter what its shape or position[180]. The use of compound rays removed the instabilities inherent in our previous approach[2, 7, 171], in which we attempted to estimate the ray sum for each individual subray from (ψ, ϕ, g) to detector pixel (α, β, g) in an algorithm we called SuperMART (Superresolution MART). Nevertheless, while FoxelCT directly calculates values for each voxel, it also, in effect, allows each subray to acquire its own subray sum. It thus also reconstructs the x-ray light field.
Generation of an Image using Foxels
We represent the focal spot as a 2D array of foxels F (a, b, g), a = 1,…aw, b = 1,…bh . Note that F(a, b, g) is an integral over an appropriate patch of S (u, v, K, µ). These are used for the back projection, calculating the reconstructed image A (x, y, z) from the detector pixel readings DE (α, β, g). In general, it is not a good idea for the rays coming from the finite elements to coincide with the rays from the foxels. The reason is that when they coincide we create what are known as pseudoprojections [181, 248, 249], which can lead to deceivingly accurate reconstructions. With foxels we are dealing with pseudoprojections when aw = ψw and bh = ϕh, making the rays and voxel weights identical for the forward and reverse calculations. Except for the pseudoprojection case, the patches of S (u, v, K, µ) used for calculating E (ψ, ϕ, g), and F (a, b, g) are different, and so are the rays and weights. When a focal spot is treated as if it were a point source, (aw,bh) = (1,1).
To represent the projection of foxel (a,b,g) onto detector pixel DF,i (α, β, g ) at iteration i we use the function WF (α, β, ψ, ϕ, x, y, z, g). The function WF describes a weight between zero and one, which we base on a line between the centers of detector pixel (α, β, g) and foxel (a,b,g) and includes the angular information in S (u, v, K, µ). The centers of the foxels are used for the calculation. The subscript F on DF,i is a reminder that foxels are used in this calculation. We may refer to all of the line segments (rays) from all of the focal spot foxels to all of the detector element centers as the reverse x-ray light field. Like WE, WF returns values based on the Wu line algorithm.
The MART algorithm works by taking the current estimate for U (x, y, z), namely Ai (x, y, z), and calculating the next estimate Ai+1(x, y, z). This is done one ray at a time. In our case here, we are dealing with compound rays, so the estimate for one compound ray from a detector pixel to all foxels contributing to it is:
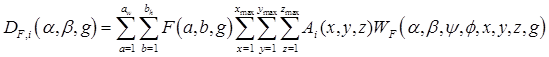 [2]
[2]
or:
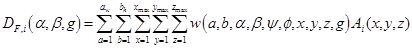
where the weight 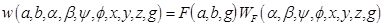 . We have formulated and used the following version of the MART algorithm:
. We have formulated and used the following version of the MART algorithm:
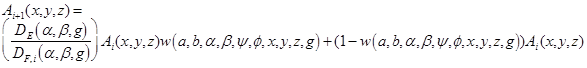 [3]
[3]
The computation is only done when 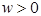 , i.e., only for those voxels that lie along the compound ray. Equation 3 came to mind because it only corrects the fraction w of a voxel that is involved in the Wu algorithm representation of a ray. Ideally, when all of the voxels in the compound ray are processed, we would have:
, i.e., only for those voxels that lie along the compound ray. Equation 3 came to mind because it only corrects the fraction w of a voxel that is involved in the Wu algorithm representation of a ray. Ideally, when all of the voxels in the compound ray are processed, we would have:
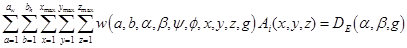 [4]
[4]
However, there are a few nuances that have yet to be analyzed in the literature. First of all, the original MART algorithm[215] was formulated for binary weights, 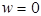 or
or 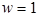 . It has been generalized to include fractional weights by the following methods, which in our present notation become:
. It has been generalized to include fractional weights by the following methods, which in our present notation become:
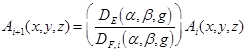 [5]
[5]
where the weights only occur in the calculation of 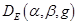 and
and 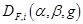 [180, 222, 232, 250], and:
[180, 222, 232, 250], and:
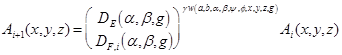 [6]
[6]
per[221, 223, 225] (and MART3 in[219]), where 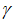 is a relaxation constant. Equation 5, summed over all voxels in a given ray, satisfies Equation 4, while in general Equation 6 does not. This discrepancy does not seem to have been discussed previously.
is a relaxation constant. Equation 5, summed over all voxels in a given ray, satisfies Equation 4, while in general Equation 6 does not. This discrepancy does not seem to have been discussed previously.
With compound rays, we have an additional complication: a given compound ray may intersect a given voxel more than once. This may be seen by rewriting Equation 4 as:
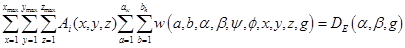 [7]
[7]
Insofar as the forward and reverse x-ray light fields coincide, the redundancies will have no effect on the results of the calculation. We find convergence anyway using Equation 3 for MART with the Xu algorithm, but further analysis will be needed to analyze the situation, and perhaps come up with yet another way to calculate and/or incorporate the weights. One way to think about the situation is that some voxels are iterated more often than others, which may prove (mathematically) to have little effect on the solution reached upon convergence.
All MART algorithms require an initial nonzero image. We start with the value A0 (x, y, z) = (Umax +1)/2, where Umax is the maximum value possible value for a voxel, 255 in this paper. Our computer program terminates once some criterion is met, such as a convergence criterion, or it can be run for a specified number of iterations. We define stopping criteria below.
Reduction of 3D equations to the 2D fan beam case
We consider reconstruction of a single slice using FoxelCT, as sketched in Figure 6:
- The patient or object is represented as U (x, y, z) with z constant, reduced to U (x, y).
- The detector pixels of width d are arranged in a one-dimensional arc requiring a single index: DE (α, β, g) is reduced to DE (α, g). Their iterated estimates DF,i (α, β, g) are reduced to DF,i (α, g).
- The focal spot S (u, v, κ, μ) is one-dimensional, curved in an arc, with flux independent of angle, reduced to S (u). In this paper, we further reduce S to a constant >0. Its area of fwfh is reduced to an arc of length fw, which is taken as an odd multiple of d. Thus, the focal spot is a uniform rectangle whose flux is independent of angle.
- The gantry position g is specified by a single angle of rotation ϴg, g=1,…G of a gantry of radius r (Figure 6a).
- The emission finite elements are arranged on an arc, reducing E (ψ, ϕ, g) to E (ψ, g), Ψ = 1…. Ψw .
- The foxels are arranged on an arc, reducing F (a, b, g) to F (a, g), a = 1,…,aw
- The reconstructed image A (x, y, z) is reduced to A (x, y).
Selection of 2D fan beam gantry angle order
It is important to consider the order of using the gantry rotation angles R = {ϴg, g = 1,…G} in a MART calculation, as it can affect the speed of convergence and the accuracy of image reconstruction[220, 251-254]. This calculation order can be independent of the order in which the angles are chosen for data acquisition, such as consecutive for rotating third or fourth generation CT scanners, or arbitrary, for scanners with multiple fixed[255], independently addressable x-ray sources. Basically, MART works fastest when consecutive angles being computed are as close to orthogonal as possible. To approximate this, we use a sequence of gantry angles inspired by the Multilevel Scheme (MLS) algorithm[251]. The MLS algorithm was originally developed for parallel projections. Our fan beam gantry angle order is calculated recursively in the following manner. We restrict ourselves to G = 2L equally spaced angles over the range [0̊ ,360̊ ), where “level” L ≥ 0 is an integer:
- We start with two mutually perpendicular angles in the string λ = {0̊ ,90̊}. Let’s call these “anchor” angles, and set R = λ.
 is initially designated as a “new” anchor angle, and
is initially designated as a “new” anchor angle, and 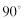 is designated as an “old” anchor angle.
is designated as an “old” anchor angle.
- If the length(R) = G stop else continue.
- For each new anchor angle ϴj :
- Generate a string of 4 angles
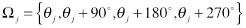 and concatenate it to the end of R to update
and concatenate it to the end of R to update 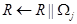 .
.
- After this concatenation designate the anchor angle ϴj as “old”.
- Between every consecutive pair of anchor angles in
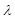 intercalate the average of the two angles and designate the intercalated angles as “new”.
intercalate the average of the two angles and designate the intercalated angles as “new”.
- Go to step 2.
In step 4 there is some liberty in the order in which the new anchor angles are processed. Since each anchor angle generates 4 angles in R, we assume that the effect of this order on the convergence would be minimal, and thus have programmed them in numerical order. The steps generating the first 32 angles are shown in Table 4. A more refined algorithm would use the set of angles for the individual rays between detector pixels and foxels instead of the gantry angles.
Table 4. MLS-like algorithm for generating the order for the gantry angles in a MART calculation. At each recursive step the new anchor angles are in bold. The last row shows the first 32 angles, in order, generated by our algorithm. Angles are specified in degrees.

Quality control
The quality of the image produced by each algorithm for iteration i can be assessed by comparing the root-mean-square sum of the differences between the “unknown” input test image U (x, y, z) and any given reconstructed image Ai (x, y, z). We took the inverse of this number, so we could achieve a scale that increases with increasing image quality:
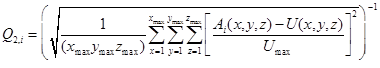 [8]
[8]
where i=1,,,k and k is the final iteration of the program, as determined by a convergence criterion. While this quality measure cannot be used with an actual unknown, it gives us a good measure of the overall accuracy of the reconstruction algorithm on test pictures U (x, y, z). The quality measure Q2,i is based on an L2 norm. We also tried the analogous L1 norm quality measure:
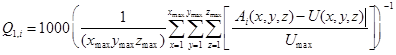 [9]
[9]
MART is known empirically[215, 222] and mathematically[216, 222, 223] to maximize the entropy of the reconstructed image, when it is defined as:
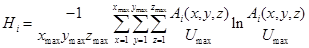 [10]
[10]
Calculation of the entropy does not depend on knowing the actual image U (x, y, z).
Stopping criterion
Iterating through the projections multiple times can refine the image, often improving image quality. However, excessive iterations of the algorithm can actually lead to worse image quality when there is an inconsistency in the simultaneous linear equations being solved[180, 181, 198, 248]. Such divergence of image quality with continued iterations can also be anticipated in our case, as slightly different sets of linear equations (rays) are being used for obtaining the forward projection data (Equation 1) and reconstructing images in a reverse manner from that data (Equation 2). Our stopping criterion is defined, such that we keep iterating through the algorithm until the quality score begins to decline, i.e., passes its first peak. Thus, the final iteration is defined as the last iteration before the decline in image quality. Our computer program allows subsequent iterations, or manual control of iterations, so that one may explore the behavior beyond this first peak. In some cases, the image quality increases monotonically for many iterations, with little improvement in the visual quality of the image. In such instances, we manually stop the run and show the final image.
Implementation
Our foxels software program was developed entirely in Java version 1.8. The program emulates two CT machines: (1) a CT scanner using the foxels MART algorithm, and (2) a CT scanner that regards the focal spot as a point source for the reverse calculation (though not for the forward calculation). The program may be run either using its Graphical User Interface (GUI), or in batch mode from the command line.
In the GUI (Figure 11), the user may try out various settings and images to see qualitatively the difference between the two machines. The command line batch mode can be used to directly generate quality scores, for various parameters.
Figure 11. User interface. The FoxelCT user interface is shown after selecting the image to reconstruct, with output shown at one iteration (“round”). The input image is converted to gray scale if it is a color image. The Bressenham “staircase” algorithm for drawing lines[256] was not explored for representing rays in this paper. Alternate convergence (stopping) criteria are: variance method, 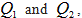 but the calculations can be continued after stopping. A log of all the input and output parameters and the current reconstructed image can be output by the SAVE command. The PLOT shows the voxel values along a horizontal line through the center of the latest reconstructed image. The SHOW command may be used to display the original input image. However, after clicking SHOW, except for the information in the log, the work done so far is lost. RESET IMAGE deletes the work done so far (except for the log text), allowing a start from scratch. It can be useful when comparing the effects of different parameters on a single image. STOP ends the program with the image that is currently displayed on the screen. That image is updated after every iteration, so the progress of the computation can be followed visually. The file name convention for the output we use in this paper is just the parameters in the order shown here, namely “Lena 3 3 3 435 57 1 7 W 1” in this example. Note h = aw. In terms of our equations, the values in the first two input rows correspond to
but the calculations can be continued after stopping. A log of all the input and output parameters and the current reconstructed image can be output by the SAVE command. The PLOT shows the voxel values along a horizontal line through the center of the latest reconstructed image. The SHOW command may be used to display the original input image. However, after clicking SHOW, except for the information in the log, the work done so far is lost. RESET IMAGE deletes the work done so far (except for the log text), allowing a start from scratch. It can be useful when comparing the effects of different parameters on a single image. STOP ends the program with the image that is currently displayed on the screen. That image is updated after every iteration, so the progress of the computation can be followed visually. The file name convention for the output we use in this paper is just the parameters in the order shown here, namely “Lena 3 3 3 435 57 1 7 W 1” in this example. Note h = aw. In terms of our equations, the values in the first two input rows correspond to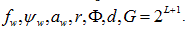
The forward projection sums in Equation 1 are calculated during the first iteration, and stored for use in subsequent iterations. If it is stopped for any reason, the projection sums are recalculated before proceeding, in case any parameters have been changed. Timings reported represent the actual run time needed for the reconstruction algorithm, not including calculation of the projection sums.
Attempt at optimization of parameters
We have a multidimensional space to explore, even within the confines of the gantry configuration we have chosen (Table 3):
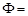 fan beam angle (Figure 6a and Figure 8).
fan beam angle (Figure 6a and Figure 8).- G = number of gantry angles, evenly spaced over 360o.
- Stopping criterion, which determines the number of iterations.
- ψw = number of finite elements used to approximate the focal spot as a continuum.
- aw = number of foxels into which the focal spot is divided for reconstruction.
- fw = focal spot width, measured in units of detector pixel width.
- d = υ i.e, detector pixel spacing = voxel spacing.
Rather than explore the whole space, we make the assumption that Qn,j (f, ψw, aw),n = 1 ᴠ 2 (Equations 9, 10) has a single maximum (i.e., is a convex function), which would then also be true of any transect. First, as patient dose is directly proportional to the number of views, we reduce G from our initial G = 256 gantry angles and see how image quality holds up. To maximize the effect of the foxel approach, we start at the high focal spot size fhigh. The second task is then to find the plateau of Qn,j (fhigh, ψw, aw), versus the number of finite elements ψw, so we can settle on a minimal value of ψw, ψmin, as the computing time is heavily dependent on ψmin. The third task is to find the peak of Qn,j (fmax, ψmin, aw) versus aw, to obtain its peak, amax. We can then explore the effect of increasing fw on image quality without and with foxels (Figure 6), making the assumptions that ψw = ψmin fw/fmax and aw = amax fw/fmax.
The FoxelCT computer program was run on a Macintosh iMac (mid-2014 21.5 inch) with a 1.4 GHz Intel Core i5 processor and on a Macintosh iMac (late-2012 27 inch) with a 3.4 GHz Intel Core i7 processor with 32 GB 1600 MHz DDR3 memory and an internal 750GB solid state disk. The computing times are reported for the latter computer. Following standard computer science practice, the order of magnitude for the computing time scales as 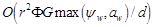 . This is verified in Figure 12.
. This is verified in Figure 12.
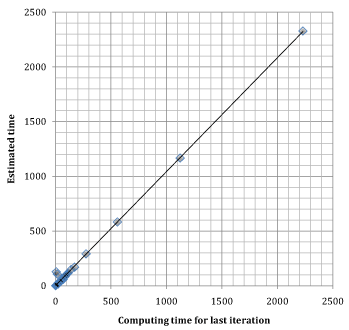
Figure 12. Actual computing time versus order of magnitude estimate. This plot of run time estimated as being proportional to a constant times 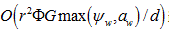 is shown. The proportionality constant is 1.1x10-7 with
is shown. The proportionality constant is 1.1x10-7 with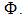 measured in degrees. The outliers are due to the time to calculate the projection sums at the first iteration. This plot is created from a sampling of our runs. The longest run we made, with file name L20 = “Lena 513 1539 439 435 57 1 7 W 30”, took 2200 seconds per iteration.
measured in degrees. The outliers are due to the time to calculate the projection sums at the first iteration. This plot is created from a sampling of our runs. The longest run we made, with file name L20 = “Lena 513 1539 439 435 57 1 7 W 30”, took 2200 seconds per iteration.
What we have fixed in advance is that all test pictures and patterns are 512x512 voxels (voxels rather than pixels, because they represent slabs with some thickness), with a gray scale of 0 to 255, and the gantry has a radius of 435 voxels (Figure 8). Along with a fan beam of 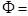 57o, these parameters are chosen to be representative of contemporary CT body scanners (Table 3). We found that the iteration at which the quality measures based on the L1 and L2 norms peaked were sometimes the same, but sometimes quite different. We ran FoxelCT on a few test patterns to check its performance while varying its input parameters:
57o, these parameters are chosen to be representative of contemporary CT body scanners (Table 3). We found that the iteration at which the quality measures based on the L1 and L2 norms peaked were sometimes the same, but sometimes quite different. We ran FoxelCT on a few test patterns to check its performance while varying its input parameters:
- Effect of reducing the angle of the fan beam
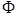 (Figure 13). Result:
(Figure 13). Result:  57o reasonably reconstructs an image except at the margins that are sometimes outside of the fan beam (Figure 8).
57o reasonably reconstructs an image except at the margins that are sometimes outside of the fan beam (Figure 8).
- Effect of the number of views G with fan beam angle
 57o (Figure 14). Result: the reconstruction holds up well at G= 128 or more views. We chose G = 256 views to be close to the common industry standard of 360 views.
57o (Figure 14). Result: the reconstruction holds up well at G= 128 or more views. We chose G = 256 views to be close to the common industry standard of 360 views.
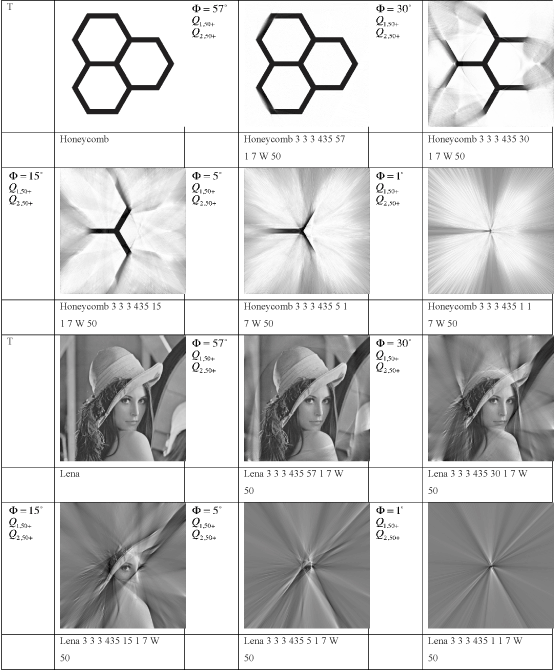
Figure 13. Effect of reducing the fan beam angle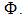 . A: T = a 512x512 voxel binary test pattern “Honeycomb”. The reconstructed images show that the center of the image is reconstructed well, with FoxelCT acting as a region of interest algorithm[227, 257, 258]. Focal spot width fw = 3 voxels represented by 3 finite elements, reconstructed with 3 foxels using 8 levels (256 equally spaced gantry angles). “50+” means 50 iterations with the + sign indicating that convergence had not been attained yet and the run was stopped manually. “50” without a plus sign would mean that the computer program stopped automatically at the peak
. A: T = a 512x512 voxel binary test pattern “Honeycomb”. The reconstructed images show that the center of the image is reconstructed well, with FoxelCT acting as a region of interest algorithm[227, 257, 258]. Focal spot width fw = 3 voxels represented by 3 finite elements, reconstructed with 3 foxels using 8 levels (256 equally spaced gantry angles). “50+” means 50 iterations with the + sign indicating that convergence had not been attained yet and the run was stopped manually. “50” without a plus sign would mean that the computer program stopped automatically at the peak  whichever norm is designated. B: T = a 512x512 voxel halftone test pattern “Lena”[259-261], reconstructed with the same parameters. Note that the inner circle (Figure 8) within which greater accuracy is achieved is now apparent. The reconstructions at
whichever norm is designated. B: T = a 512x512 voxel halftone test pattern “Lena”[259-261], reconstructed with the same parameters. Note that the inner circle (Figure 8) within which greater accuracy is achieved is now apparent. The reconstructions at  1o confirm that the coded geometry of the fan beams is properly centered. File names under each reconstructed image correspond to the input parameters in the order shown in Figure 11.
1o confirm that the coded geometry of the fan beams is properly centered. File names under each reconstructed image correspond to the input parameters in the order shown in Figure 11.
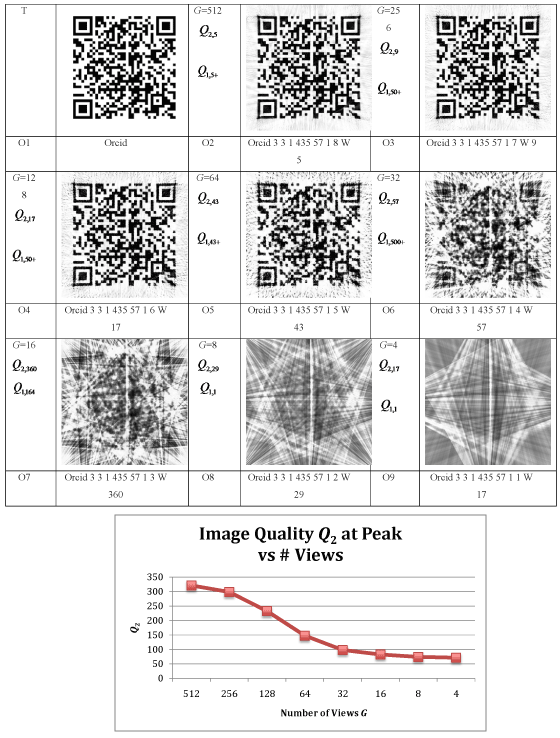
Figure 14. A: Effect of the number of views. Here the fan beam angle is held constant at  57o, and the number of levels L is reduced by powers of 2. T = 512x512 binary test pattern, a Quick Read, QR code. Reconstructions are then with 512 down to 4 evenly spaced gantry angles (views). Focal spot width ƒ= 3 voxels represented by 3 finite elements, foxel width ƒ= 1 voxel. With one exception (16 views) the peak for the L2 norm came at fewer iterations than the L1 norm. The images shown here are for the L2 norm stopping criterion. Visually further iterations made no difference. A + sign indicates that a peak value hadn’t been reached at the specified number of iterations. B: Image quality versus number of views or gantry positions equally spaced over 360o shows only a small decline for 256 views, which we used for subsequent simulations.
57o, and the number of levels L is reduced by powers of 2. T = 512x512 binary test pattern, a Quick Read, QR code. Reconstructions are then with 512 down to 4 evenly spaced gantry angles (views). Focal spot width ƒ= 3 voxels represented by 3 finite elements, foxel width ƒ= 1 voxel. With one exception (16 views) the peak for the L2 norm came at fewer iterations than the L1 norm. The images shown here are for the L2 norm stopping criterion. Visually further iterations made no difference. A + sign indicates that a peak value hadn’t been reached at the specified number of iterations. B: Image quality versus number of views or gantry positions equally spaced over 360o shows only a small decline for 256 views, which we used for subsequent simulations.
- Effect of the number of iterations. It became clear that the correlation between our image quality measures and the visual impression of quality of the reconstruction was not high (Figure 15). For this reason, we did not try to use the entropy as a proxy measure of image quality. As it is not our purpose here to find the best image quality measure, especially because it may be image and parameter dependent, we allowed our visual impression to override the image quality measures in choosing which iteration to illustrate.
Figure 15. A: Effect of the number of iterations on image quality. For all reconstructions, here we set focal spot width ƒw= 21 voxels, ψ w = 5 finite elements, reconstructed with aw = 11 foxels. The number of iterations i is varied. The fan beam is  57o and G 256 views are used. Both of the L1 and L2 based quality measures
57o and G 256 views are used. Both of the L1 and L2 based quality measures  peaked at iteration i = 2. Their values are listed respectively for each iteration. While this is an unlikely set of parameters, with
peaked at iteration i = 2. Their values are listed respectively for each iteration. While this is an unlikely set of parameters, with 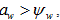 it illustrates that simple image quality measures cannot be used without visually checking on them. B: Checking the images against the graph, we have the counterintuitive conclusion that the visual quality increases while the quantitative quality measures decline. Squares are
it illustrates that simple image quality measures cannot be used without visually checking on them. B: Checking the images against the graph, we have the counterintuitive conclusion that the visual quality increases while the quantitative quality measures decline. Squares are 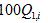 and triangles are
and triangles are 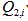 versus iteration i.
versus iteration i.
- Effect of varying the number of finite elements into which the focal spot is divided (Figure 16). We tested a focal spot width of
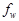 = 21 voxels wide, i.e., fw = 21d, fixing the number of foxels at aw = 1. From this we decided to use 3 finite elements per voxel of the focal spot width, i.e., a finite element width of
= 21 voxels wide, i.e., fw = 21d, fixing the number of foxels at aw = 1. From this we decided to use 3 finite elements per voxel of the focal spot width, i.e., a finite element width of 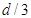 .
.
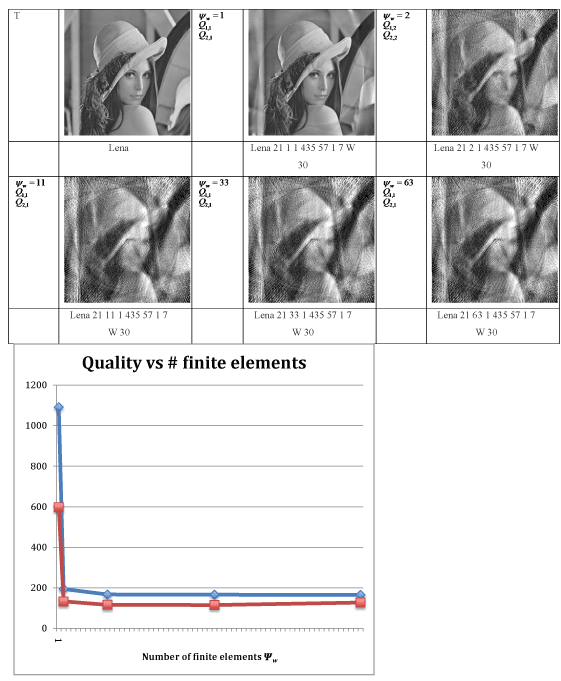
Figure 16. Effect of the number of finite elements 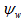 used to represent a focal spot. A: For all reconstructions, here we set focal spot width
used to represent a focal spot. A: For all reconstructions, here we set focal spot width 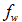 = 21 voxels, reconstructed with aw = 1 foxel. Thus, a wide focal spot is treated as if it were a point source. The number of finite elements
= 21 voxels, reconstructed with aw = 1 foxel. Thus, a wide focal spot is treated as if it were a point source. The number of finite elements 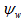 used to represent the focal spot is varied. The fan beam is
used to represent the focal spot is varied. The fan beam is 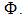 57o and G = 256 views are used. The first peak iterations for the L1 and L2 based quality measures are given. Given the experience of Figure 15, all reconstructions are shown at 30 iterations. B: As real focal spots are a continuum, the image for
57o and G = 256 views are used. The first peak iterations for the L1 and L2 based quality measures are given. Given the experience of Figure 15, all reconstructions are shown at 30 iterations. B: As real focal spots are a continuum, the image for 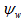 = 63 is the most realistic, which represents 3 finite elements per voxel width of the focal spot
= 63 is the most realistic, which represents 3 finite elements per voxel width of the focal spot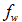 . The near perfection of the reconstruction with
. The near perfection of the reconstruction with 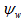 = 1 is an artefact of a zero width of the finite element representation in this case, since we only use the center point of each finite element in calculating the projection sums. It is also a pseudoprojection situation, as the rays used for the projection sums and reconstruction are identical.
= 1 is an artefact of a zero width of the finite element representation in this case, since we only use the center point of each finite element in calculating the projection sums. It is also a pseudoprojection situation, as the rays used for the projection sums and reconstruction are identical.
- Effect of increasing the number of foxels. Again, we used a focal spot width of
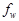 = 21 voxels, with 63 finite elements, and varied the number of foxels. The image quality at iteration 30 increases up until 18 foxels, after which it collapses completely with further iteration (Figure 17). This behavior may be related to an analogous improvement with and then collapse of Power MART at a critical value of an exponent[221, 225]. This led to the ratio
= 21 voxels, with 63 finite elements, and varied the number of foxels. The image quality at iteration 30 increases up until 18 foxels, after which it collapses completely with further iteration (Figure 17). This behavior may be related to an analogous improvement with and then collapse of Power MART at a critical value of an exponent[221, 225]. This led to the ratio 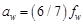 , which we shall assume is near optimal for all subsequent reconstructions. It is consistent with the observation that “…over-aggressive model parameters introduce reconstruction artifacts and degrade resolution”[185].
, which we shall assume is near optimal for all subsequent reconstructions. It is consistent with the observation that “…over-aggressive model parameters introduce reconstruction artifacts and degrade resolution”[185].

Figure 17. Effect of increasing the number of foxels. A: Here we use a focal spot width of 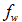 = 21 voxels, with 3 finite elements per voxel, i.e.,
= 21 voxels, with 3 finite elements per voxel, i.e., 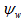 = 63. The number of foxels h is varied, and all reconstructions are shown at 30 iterations. The first two Q’s give the iterations at which they first peaked, followed by their values at iteration 30. At aw = 1 this broad focal spot is treated as if it were a point source. We can see that improvement in image quality over this current practice, as measured at iteration 30, peaks versus number of foxels at aw = 18. The peak image quality as visually assessed seems to be at aw = 18 or aw = 19. Image quality visibly collapses starting at aw = 20 and a few samples at higher values of aw suggest that it does not return. One clue to this behavior may be that, for instance, for aw = 22, there were second peaks versus iteration at the 4th iteration. B,C: In this set of simulations, the quantitative quality measures correspond to the visual quality. The diamonds show each Q value at its peak iteration and the squares show the Q values at the 30th iteration. The sudden collapse of the image is apparent. This critical number of foxels for the given focal spot width
= 63. The number of foxels h is varied, and all reconstructions are shown at 30 iterations. The first two Q’s give the iterations at which they first peaked, followed by their values at iteration 30. At aw = 1 this broad focal spot is treated as if it were a point source. We can see that improvement in image quality over this current practice, as measured at iteration 30, peaks versus number of foxels at aw = 18. The peak image quality as visually assessed seems to be at aw = 18 or aw = 19. Image quality visibly collapses starting at aw = 20 and a few samples at higher values of aw suggest that it does not return. One clue to this behavior may be that, for instance, for aw = 22, there were second peaks versus iteration at the 4th iteration. B,C: In this set of simulations, the quantitative quality measures correspond to the visual quality. The diamonds show each Q value at its peak iteration and the squares show the Q values at the 30th iteration. The sudden collapse of the image is apparent. This critical number of foxels for the given focal spot width 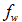 may be some kind of phase transition.
may be some kind of phase transition.
- Effect of increasing the focal spot size regarded as a point source versus using foxels. We next considered image quality as the focal spot width fw is increased from 1 to 513 = 29 + 1 voxel widths. The latter equals the width of the image being reconstructed. Image quality is severely reduced from fw = 17 = 24+ 1 if the focal spot is treated as a point source in the CT computation. However, if foxels are used, the focal spot size can be increased roughly by a factor of 4 while retaining equivalent visual image quality of the face of Lena (Figure 18). Visually, the reconstruction with foxels remains recognizable as a face all the way to fw = 513, i.e., with a focal “spot” as wide as the image being reconstructed. While the image quality factors are sustained to larger focal spot sizes (Figure 19 and Figure 18), they cannot be taken as reliable measures of visual image quality.
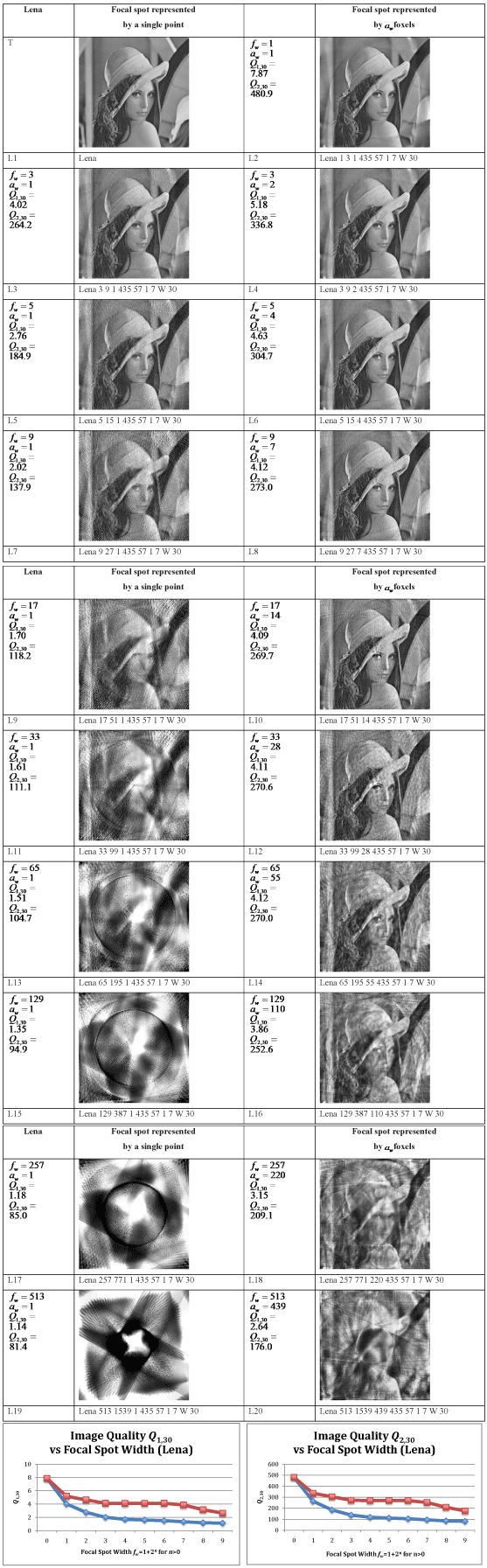
Figure 18. Effect of increasing the focal spot size regarded as a point source versus using foxels, for Lena test image. A: Left column: point source. Right column: foxel source. Here we use 3 finite elements per voxel width of the focal spot, i.e., 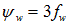 . Images are at 30 iterations. The focal spot width fw is increased in powers of 2, with 1 added to get an odd number, so that the fan beam has a central ray. The number of foxels aw is proportional to the focal spot width. The peak image quality for a focal spot width of fw = 21 was reached with 18 foxels in Figure 17. Here we maintain this ratio:
. Images are at 30 iterations. The focal spot width fw is increased in powers of 2, with 1 added to get an odd number, so that the fan beam has a central ray. The number of foxels aw is proportional to the focal spot width. The peak image quality for a focal spot width of fw = 21 was reached with 18 foxels in Figure 17. Here we maintain this ratio:  where the brackets indicate truncation to the nearest integer. For wide focal spots, foxels lead to substantially greater image quality than the point source approximation (consistent with[179]). Wide focal spots also generate a recognizable image at focal spot sizes so large that they are as wide as the image itself. B,C: The two graphs of image quality measures
where the brackets indicate truncation to the nearest integer. For wide focal spots, foxels lead to substantially greater image quality than the point source approximation (consistent with[179]). Wide focal spots also generate a recognizable image at focal spot sizes so large that they are as wide as the image itself. B,C: The two graphs of image quality measures  and
and 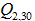 show that the quality is always higher when foxels are used (squares) than approximation of the focal spot as a point source (diamonds). However, these measures do not reflect visual image quality. Note that 0 on the abscissa corresponds to a point source.
show that the quality is always higher when foxels are used (squares) than approximation of the focal spot as a point source (diamonds). However, these measures do not reflect visual image quality. Note that 0 on the abscissa corresponds to a point source.

Figure 19. The 512x512 voxel test pattern Lena shows that image quality holds up much better as the focal spot width fw is increased, here up to 17 times the detector pixel width, than reconstructions approximating the focal spot as a point source. T = input test pattern. Details in Figure 18.
Having selected a gantry configuration, number of views (gantry angles), number of iterations to reasonable convergence, minimum number of finite elements per unit width of the focal spot, and a maximum threshold for the usefulness of foxels aw = (6/7) fw, we applied these parameters to sections of the Visible Human Male (Figures 20, Figures [21-22]). Two observations are apparent: 1) the fine detail on the head CT (Figures 20 and Figure 23) does not permit as great an increase in focal spot width fw as for the Lena test image; 2) approximation of the focal
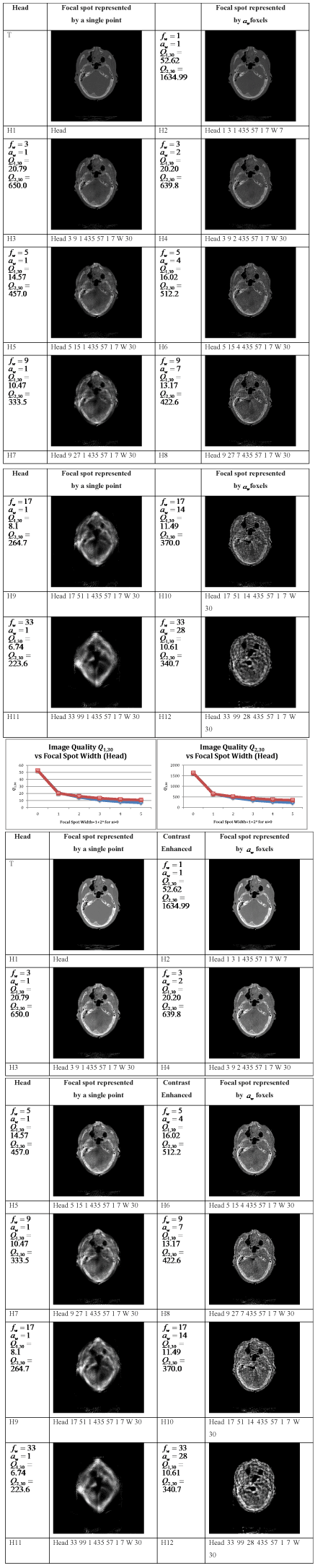
Figure 20. Effect of increasing the focal spot size regarded as a point source versus using foxels for Head CT. A: For caption details see Figure 18. B,C: Graphs show the decline of quantitative image quality as the focal spot size is increased, but do not distinguish the point source approximation from reconstructions made with foxels. D: To enhance the contrast, we have also shown the same reconstructions processed via the Compositor Autolevel function.
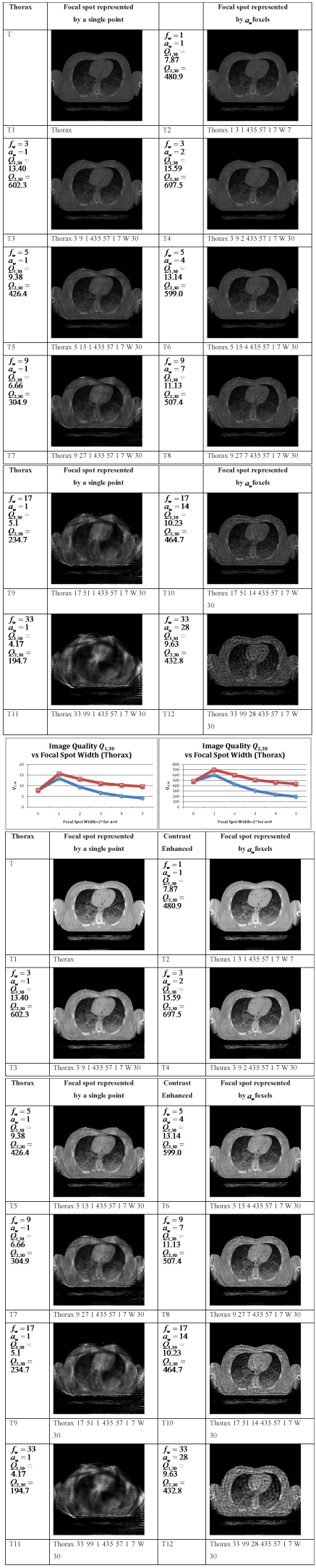
Figure 21. Effect of increasing the focal spot size regarded as a point source versus using foxels for Thorax CT. For caption details see Figure 18 and Figure 20. In this case the quantitative quality measures do distinguish the point source approximation from the use of foxels.
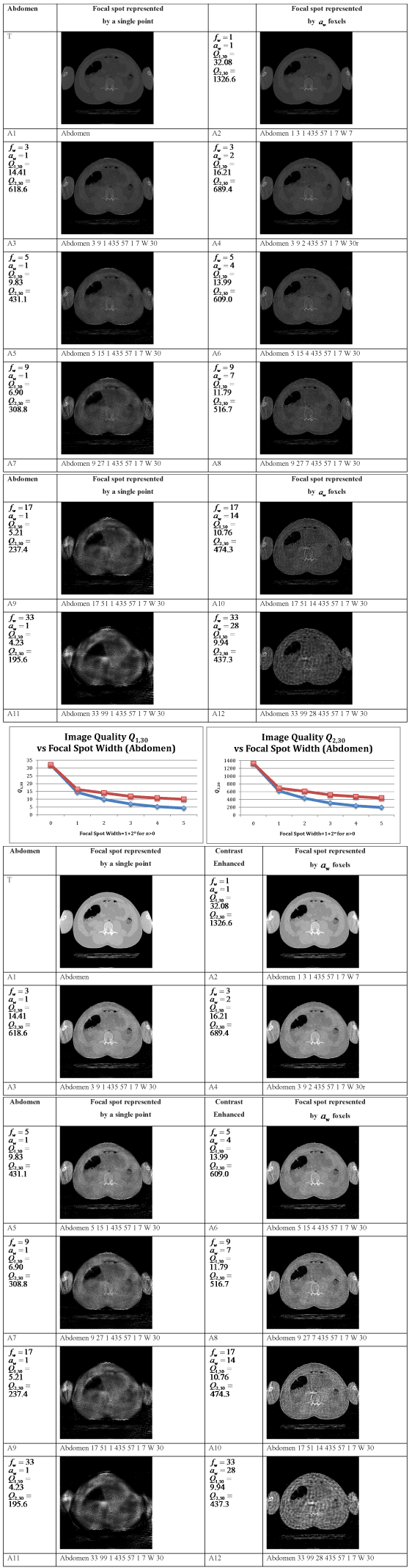
Figure 22. Effect of increasing the focal spot size regarded as a point source versus using foxels for Abdomen CT. For caption details see Figure 18 and Figure 21.
spot as a point source not only results in poorer image quality, but also distorts the geometry of the skull.
Our results, summarized in Figure 19 and Figure 23, show considerable improvement for the use of foxels over the point source approximation, warranting the use of foxels in any x-ray imaging situation. These images are suboptimal, in that we used the convexity of the parameter space to get somewhere near the optimal peak, but with further exploration via simulation that peak may be discoverable. It is possible that peak performance of foxels is image dependent.
We confined our simulation to a rectangular focal spot of uniform flux and did not consider that different parts of the x-ray focal spot may have different intensities (Figure 7). In other words, we always used E = F = 1 in Equations 1, 2 and 3. As it has been shown that the projection images of small objects are distorted by the pattern of intensity variations in the focal spot[28], with inhomogeneity increasing with tube current[9], any means of improving the uniformity of focal spots is likely to improve imaging. However, the use of foxels could directly correct for nonuniformity. The effects of nonuniformity on FoxelCT reconstructions has yet to be explored.
Foxels are applicable to all projection radiography, classical tomography in digital form, tomosynthesis, and CT in all its variations of gantries, including inverse geometries, and should improve imaging in every case. However, one may ask if there is an optimal foxel solution to the 3D imaging problem. For an array of point sources of x-rays, optimality has recently been claimed for a particular tetrahedral configuration for cone-beam CT[262]. The authors invoke notions of four flexible detectors that would be wrapped over a spherical cap forming the intersection of a cone beam emanating from one of the four tetrahedrally arranged point sources (Figure 24). As we have illustrated there, a smaller cap representing a broad focal spot could be added, which could be divided into foxels. This is a 3D version of Figure 6. The spherical chamber is not unprecedented. Michael J. Neumann (personal communication, around 1970), brother of John von Neumann[263], proposed a spherical walk-in chamber for positron tomography with detectors over the whole inner surface. Rather than coming from a standard x-ray tube, the “focal spot” could be a large area x-ray source such as is used in decontamination devices and the study of electromagnetic pulse effects[97, 114, 137, 264-266]. Flying spot x-ray sources, such as are used in reverse geometry x-ray imaging[267], could possibly provide a moving large area source by defocussing the electron beam.
Figure 23. The tetrahedron scanner. In an optimized tetrahedron scanner, each of the four x-ray sources located on the outer sphere is collimated to a cone of half angle 27o22’. (a) a single cone. (b) all 4 cones shown overlapped, each in a different color. From[262] with kind permission of Ivan B. Ye and SPIE Publications. The inner sphere, which is scanned by all 4 cones, has a radius of 0.460 of the radius of the outer sphere. The authors propose that the four spherical caps defined by the intersections of the cones with the surface of the outer sphere would be covered with flexible electronics containing the detectors. We add the notion that the apex of the cone could be extended from a point to a spherical cap (region with yellow stars added) representing a broad x-ray source that could be virtually represented as an array of foxels.
We have taken advantage of a presumed convexity of the parameter space to obtain what are thereby undoubtedly suboptimal, but provocative results. More massive computations to search the parameter space for actual maxima of visual and quantitative measures of image quality, and to what extent they are object dependent, are warranted.
We decided to do our comparisons by visual criteria using a well known, standard test picture of a young woman, Lena, widely used in computer science[259, 261]. Human perception of image quality of a human face[268] takes into account many factors that are hard to appreciate in quantitative test patterns and quantitative image quality measures. We have already shown that standard CT algorithms, including MART, especially in limited view situations, select what can be the wrong image from the infinite space of solutions to CT equations[2, 235, 269]. Others have shown how compressive sensing algorithms may improve the selection of solutions of underdetermined CT equations[270-274] such as Equation 2. Human guided reconstruction of CT images can exceed[163] the accomplishments of compressive sensing CT. For limited view problems, deconvolution of the point spread function of FoxelCT might further improve imaging[269]. There are thus many opportunities to improve upon and optimize the foxel approach.
We reached the opposite conclusion of another paper: “…that RM [ray modelling] is not necessary in clinical CT to achieve resolution recovery”[125]. We propose the use of large focal spots, rather than considering them “exaggerated” or “unrealistic” [125]. The major differences in our approaches are that these authors fix the detector size at d=1.3 mm, whereas we argue for much smaller detectors for clinical CT, emphasizing that the ratio of focal spot width fw to detector pixel width should be greatly increased, along with the ratio of focal spot width to gantry diameter. They also approximate their fw = 0.5 mm focal spot by a Gaussian, whereas we use a rectangular emission distribution, meaning that their effective focal spots are narrower than those we simulate. Given that the ratio fw /d = 0.38 or less, even with their foxel-like simulation, they are simulating what is very close to a point source, which may explain why “no visual improvement could be achieved”. Their “needle beams”, which correspond to rays from a foxel to a detector pixel, are averaged, whereas we concatenate them into a compound ray that permits different reconstructed values along each “needle beam”. We distinguish a finite element representation of the focal spot from the foxels used for reconstruction. Finally, they accept the photon noise limitations per detector measurement, whereas we chose to simulate the ideal case, leaving noise considerations to further work. We think this is reasonable, since there are other ways to reduce noise, such as lowering the number of views while increasing the dose per view, as in CT mammography[275, 276]. This will be especially important for body CT scanners with fixed arrays of x-ray sources (and no moving parts, cf. the Hula-Hoop CT scanner[277]), which may be limited to far fewer than the industry standard of 360 views or more for a rotating gantry.
It may be objected that FoxelCT is a computationally expensive algorithm that, if implemented, could reduce patient throughput. It took about 15 years before the issue of dose reduction in CT was taken seriously (Figure 25). This was an example of a trade-off between patient safety and image quality. Now we are faced with the further trade-off between image quality (usually presumed to be a measure of diagnostic accuracy) and the computer time needed to achieve higher image quality[2, 186, 201] (Figure 12), especially because faster scanners[4, 274, 278] mean less time to do the computing. Certainly Moore’s Law applies here[279, 280], as well as in other domains[281-283], as we have not yet reached limits to computer speed. Projecting 15 years they might be 215 = 32,768 times faster. Thus, in planning new CT scanners, diagnostic quality should not be sacrificed because of anticipated long computing times. The computers will catch up. For example, each slice could be run in a different thread in a multicore computer[284, 285], and CT algorithms that take advantage of parallel computers[2, 286-290] are available.
Figure 24. Papers on tomography dose versus year. The data is via the Topic search tomog* dos* in Web of Science. The earlier papers are on classical tomography. The first paper on dose reduction in CT was published in 1976[291]. It was thus 15 years before the idea took off.
Our purely geometric approach places an upper bound on what is achievable with foxels, and thus provides a goal to guide further efforts[278]. The use of foxels (focal spot pixels) in a computed tomography algorithm allows us to increase the ratio of the focal spot width to detector pixel width substantially, by a visually estimated factor of around 2 to 4, without loss of resolution compared to approximating the focal spot as a point source. If this result carries over to three dimensional CT, the area of the focal spot could thereby increase by a factor of 4 to 16, with a corresponding increase in x-ray flux. The standard approximation of the focal spot as a point source not only produces worse images than foxels in terms of image quality measures, but also distorts the anatomy. One should presume that some such distortion is present even for small focal spots approximated as a point source. Foxels allow better trade-offs in terms of scanning speed, patient dose, and spatial resolution than hitherto possible. Foxels should also enhance the resolution of digital projection radiology imaging, by correcting for the penumbra effect.
A new method for calculating the focal spot image as seen from any position in the 3D space between the focal spot and the detector array[292] could make FoxelCT quite practical.
For any given focal spot size, approximating it as a point is always worse than using foxels. Therefore, existing scanners could be immediately enhanced in image quality via incorporation of foxels in their software. Future scanners could take advantage of foxels to increase the ratio of focal spot size to detector pixel size, via bigger focal spots and/or smaller detector pixels.
We would like to thank Glen D. Colquhoun for his early work on programming foxels, which kept the idea alive, and his comments on the manuscript. Natalie K. Gordon kindly ran the Compositor program for us.
The authors have no conflicts of interest to disclose.
- Kalos MH, Davis SA, Mittelman PS, Mastras P (1961) Conceptual Design of a Vapor Fraction Instrument [http://www.osti.gov/energycitations/product.biblio.jsp?query_id=0&page=0&osti_id=4837780]. White Plains, NY, Nuclear Development Corporation of America.
- Gordon R (2011) Stop breast cancer now! Imagining imaging pathways towards search, destroy, cure and watchful waiting of premetastasis breast cancer. In: Breast Cancer - A Lobar Disease. Tot T, (Ed.). London, Springer: 167-203.
- Hounsfield GN (1977) The E.M.I. scanner. Proc R Soc Lond B Biol Sci 195: 281-289. [crossref]
- Neculaes VB, Edic PM, Frontera M, Caiafa A, et al. (2015) Multisource x-ray and CT: Lessons learned and future outlook. IEEE Access 2: 1568-1585.
- Rack A, Garcia-Moreno F, Schmitt C, Betz O, Cecilia A, et al. (2010) On the possibilities of hard X-ray imaging with high spatio-temporal resolution using polychromatic synchrotron radiation. Journal of X-ray Science and Technology 18: 429-441.
- Makeev A, Clajus M, Snyder S, Wang XL, Glick SJ (2015) Evaluation of position-estimation methods applied to CZT-based photon-counting detectors for dedicated breast CT. Journal of Medical Imaging 2: #023501.
- Colquhoun GD, Gordon R (2005) A superresolution computed tomography algorithm for reverse cone beam 3D x-ray mammography [PowerPoint presentation]. In: Workshop on Alternatives to Mammography, Copenhagen, September 29-30, 2005. Tot T, (Ed.). Alonsa, Manitoba, Canada, Silver Bog Research Inc.
- Zhang Y, Wu XX, Yang W, Feng QJ, Chen WF (2014) Super-resolution reconstruction for 4D computed tomography of the lung via the projections onto convex sets approach. Medical Physics 41: #111917.
- Mattsson O (1968) Focal spot variations with exposure data--important factors in daily routine. Acta Radiologica Diagnosis (Stockholm) 7: 161-169.
- Beetlestone A, Thurmer G (1958) Some considerations of focal spot sizes. British Journal of Radiology 31: 492-496.
- Robinson A, Grimshaw GM (1975) Measurement of the focal spot size of diagnostic x-ray tubes--a comparison of pinhole and resolution methods. British Journal of Radiology 48: 572-580.
- Nielsen B (1980) Measurement of the focal spot size of diagnostic X-ray tubes by the pinhole camera technique. The influence of the pinhole on the measured focal spot size. Health Phys 38: 683-686. [crossref]
- Kimme-Smith C, Bassett LW, Gold RH (1988) Focal spot size measurements with pinhole and slit for microfocus mammography units. Medical Physics 15: 298-303.
- Rao GU, Bates LM (1970) Effective dimensions of roentgen tube focal spots based on measurement of the modulation transfer function. Acta Radiologica: Therapy, Physics, Biology 9: 362-368.
- KEMP FH, NICHOLS AF (1958) Focal spot sizes. Br J Radiol 31: 486-488. [crossref]
- Bergeron RT (1974) Manufacturers' designation of diagnostic x-ray tube focal spot size: a time for candor. Radiology 111: 487-488.
- Bakus AD, Lin PJ (1983) A note on the measurement of focal spot sizes utilizing star test patterns at low magnification factors. Medical Physics 10: 100-103.
- Madsen JU (1989) Focal spot size measurements for microfocus X-ray sets. NDT International 22: 292-296.
- Bookstein JJ, Steck W (1971) Effective focal spot size. Radiology 98: 31-33. [crossref]
- Doi K, Loo LN, Chan HP (1982) X-ray tube focal spot sizes: comprehensive studies of their measurement and effect of measured size in angiography. Radiology 144: 383-393.
- Behling R (2015) Modern Diagnostic X-Ray Sources: Technology, Manufacturing, Reliability, CRC Press.
- Miao JW, Hodgson KO, Ishikawa T, Larabell CA, LeGros MA, et al. (2003) Imaging whole Escherichia coli bacteria by using single-particle x-ray diffraction. Proceedings of the National Academy of Sciences of the United States of America 100: 110-112.
- Tkachuk A, Duewer F, Cui H, Feser M, Wang S, et al. (2007) X-ray computed tomography in Zernike phase contrast mode at 8 keV with 50-nm resolution using Cu rotating anode X-ray source. Zeitschrift für Kristallographie 222: 650-655.
- Panetta D (2016) Advances in X-ray detectors for clinical and preclinical Computed Tomography. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 809: 2-12.
- Burger GCE (1943) The limits of vision in X-ray examinations. In: Proceedings of the 29th Dutch Physical and Medical Congress(Ed.): 286.
- Nice CM Jr (1980) Medical images: past, present, and future. Crit Rev Diagn Imaging 14: 73-109. [crossref]
- 27. Berman AI (1950) A method for increasing the safe power input of x-ray tubes. Review of Scientific Instruments 21: 275-279.
- FRANTZELL A (1951) Effect of focal size, shape and structure on the roentgenographic representation of small-calibre metal objects. Acta radiol 35: 265-276. [crossref]
- EDMONDS EW (1955) Focal spot size variation with alteration in applied potential and tube current. Radiography 21: 247-248. [crossref]
- ABEL MS (1956) Advantages and limitations of the 0.3-mm. focal spot tube for magnification and other technics. Radiology 66: 747-752. [crossref]
- Ishimura T, Shiraiwa T, Sawada M (1957) The input power limit of the cylindrical rotating anode of a x-ray tube. Journal of the Physical Society of Japan 12: 1064-1070.
- SPARKS OJ, SHEPARD RD (1957) Practical application of the 0.3-mm. focal spot; a special cassette holder. Radiology 69: 578-580. [crossref]
- KUNTKE AH (1957) On the determination of roentgen tube focal spot sizes by pin-hole camera roentgenography. Acta radiol 47: 55-64. [crossref]
- Benness GT (1964) The influence of focal spot size on image quality. Journal of the College of Radiologists of Australasia 46: 295-296.
- Doi K (1965) Optical transfer functions of the focal spot of x-ray tubes. American Journal of Roentgenology, Radium Therapy and Nuclear Medicine 94: 712-718.
- RGopala Rao UV, Bates LM (1969) The modulation transfer functions of x-ray focal spots. Phys Med Biol 14: 93-106. [crossref]
- Sakuma S, Ayakawa Y, Okumura Y, Maekoshi H (1969) Determination of focal-spot characteristics of microfocus x-ray tubes. Invest Radiol 4: 335-339. [crossref]
- Friedman PJ, Greenspan RH (1969) Observations on magnification radiography. Visualization of small blood vessels and determination of focal spot size. Radiology 92: 549-557.
- Sakuma S, Kato T, Fujita T (1969) [Direct enlargement cineradiography using a 0.5 mm focal spot X-ray tube]. Nihon Igaku Hoshasen Gakkai Zasshi 28: 1506-1509. [crossref]
- RGopala Rao UV, Bates LM (1969) The modulation transfer functions of x-ray focal spots. Phys Med Biol 14: 93-106. [crossref]
- Sakuma S, Ayakawa Y, Fujita T (1970) [Macroroentgenography in twentyfold magnification taken by means of 50 mu focal spot x-ray tube and evaluation of its reduced image]. Nippon Igaku Hoshasen Gakkai Zasshi 30: 205-209.
- Nadel JA, Cabezas GA, Austin JH (1971) In vivo roentgenographic examination of parasympathetic innervation of small airways. Use of powdered tantalum and a fine focal spot x-ray tube. Investigative Radiology 6: 9-17.
- Horowitz P, Howell JA (1972) A scanning x-ray microscope using synchrotron radiation. Science 178: 608-611. [crossref]
- Hounsfield GN (1973) Computerized transverse axial scanning (tomography). 1. Description of system. British Journal of Radiology 46: 1016-1022.
- Chaney EL, Hendee WR (1974) Effects of x-ray tube current and voltage on effective focalspot size. Med Phys 1: 141-147. [crossref]
- Doi K, Fromes B, Rossmann K (1975) New device for accurate measurement of the x-ray intensity distribution of x-ray tube focal spots. Med Phys 2: 268-273. [crossref]
- Haus AG, Doi K, Chiles JT, Rossmann K, Mintzer RA (1975) The effect of geometric and recording system unsharpness in mammography. Investigative Radiology 10: 43-52.
- Timothy JG, Bybee RL (1975) Two-dimensional photon-counting detector arrays based on microchannel array plates. Review of Scientific Instruments 46: 1615-1623.
- Henry JP, Kellogg EM, Briel UG, Murray SS, Van Speybroeck LP, et al. (1977) High resolution imaging x-ray detector for astronomical measurements. Proceedings of the SPIE 106: doi: 10.1117/1112.955472.
- Catura RC, Smithson RC (1979) Single photon x-ray detection with a CCD image sensor. Rev Sci Instrum 50: 219. [crossref]
- Kujoory MA, Hillman BJ, Barrett HH (1980) High-resolution computed-tomography of the normal rat nephrogram. Investigative Radiology 15(2): 148-154.
- Ritman EL, Kinsey JH, Robb RA, Harris LD, Gilbert BK (1980) Physics and technical considerations in the design of the DSR: High temporal resolution volume scanner. American Journal of Roentgenology 134: 369-374.
- Feeney DA, Gordon BJ, Johnston GR, McClanahan SL, Jessen CR (1982) A 200 centimeter focal spot-film distance (FFD) technique for equine thoracic radiography. Veterinary Radiology 23: 13-19.
- Behrenbeck T, Kinsey JH, Harris LD, Robb RA, Ritman EL (1982) Three-dimensional spatial, density, and temporal resolution of the dynamic spatial reconstructor. Journal of Computer Assisted Tomography 6: 1138-1147.
- Law J, Kirkpatrick AE (1988) The influence of focal spot size on image qualityin mammography. British Journal of Radiology 61: 763.
- Hüttenbrink KB, Paldauf E, Brinkmann B (1989) Vorstellung einer neuen Untersuchungsmethode in der Rechtsmedizin: Die hochgradige direkte Röntgenvergrößerung mit einer 1µ-Focus-Röntgenröhre/Demonstration of a new technique in forensic medicine the high grade direct radiographic magnification with a 1-mu focal spot tube [German]. Archiv für Kriminologie 183: 1-10.
- Feldkamp LA, Goldstein SA, Parfitt AM, Jesion G, Kleerekoper M (1989) The direct examination of three-dimensional bone architecture in vitro by computed tomography. Journal of Bone and Mineral Research 4: 3-11.
- Glüer CC1, Dix WR, Engelke K, Graeff W, Kupper W, et al. (1989) A fast low-noise line scan x-ray detector. Med Phys 16: 98-104. [crossref]
- Doyum AB, Nabel E (1991) A practical and convenient method for the measurement of focal spots of industrial x-ray tubes. NDT & E International 24: 145-149.
- Nagata Y, Yamaji H, Hayashi K, Kawashima K, Hyodo K, Kawata H, Ando M (1992) High energy high resolution monochromatic x-ray computed tomography using the Photon Factory vertical wiggler beamline. Review of Scientific Instruments 63: 615-618.
- Boone JM, Alexander GM, Seibert JA (1993) A fluoroscopy-based computed tomography scanner for small specimen research. Investigative Radiology 28: 539-544.
- Law J (1993) The influence of focal spot size on image resolution and test phantom scores in mammography. Br J Radiol 66: 441-446. [crossref]
- Holdsworth DW, Drangova M, Fenster A (1993) A high-resolution XRII-based quantitative volume CT scanner. Medical Physics 20: 449-462.
- Albert TM (1993) Large-area scanning-x-ray source to maximize contrast sensitivity by minimizing scatter detection. Proceedings of the SPIE 2009: 12-21.
- Tang S, Barnes GT, Tanner RL (1995) Slit camera focal spot measurement errors in mammography. Medical Physics 22(11 Pt 1): 1803-1814.
- Young KC, Ramsdale ML, Rust A (1995) Survey of mammography image quality in the UK. Radiation Protection Dosimetry 57: 163-165.
- Speller RD, Martínez-Dávalos A, Farquharson M (1995) A CCD based focal spot camera. Phys Med Biol 40: 315-321. [crossref]
- Court LE, Speller R (1995) A multiparameter optimization of digital mammography. Phys Med Biol 40: 1841-1861. [crossref]
- Platin E, Mauriello S, Ludlow JB (1996) Effects of focal spot size on caries diagnosis with D and E speed images. Oral Surg Oral Med Oral Pathol Oral Radiol Endod 81: 235-239. [crossref]
- Toye D, Marchot P, Crine M, Lhomme G (1996) Modelling of multiphase flow in packed beds by computer-assisted x-ray tomography. Measurement Science and Technology 7: 436-443.
- Aoki S, Takeuchi A, Sakurai K, Kameno H, Saito D, et al. (1997) Submicron X-ray microbeam production with a Wolter-type grazing incidence mirror at Tristan Main Ring (KEK). Journal de Physique IV 7(C2): 329-330.
- Goodsitt MM, Chan HP, Liu B (1997) Investigation of the line-pair pattern method for evaluating mammographic focal spot performance. Med Phys 24: 11-15. [crossref]
- Krol A, Huda W, Chamberlain CC, Kieffer JC, Jiang ZM, Yu JF (1998) Ultra-small focal spot x-ray sources for high resolution digital mammography. In: Digital Mammography. Karssemeijer N, Thijssen M, Hendriks J, VanErning L, (Ed.), Springer. 13: 43-46.
- Gambaccini M, Tuffanelli A, Del Guerra A, Taibi A, Zanca F (1998) Resolution properties of a large area quasi-monochromatic X-ray source for mammography. Proceedings of the SPIE 3336: 65-74.
- Weisfield RL, Hartney MA, Street RA, Apte RB (1998) New amorphous-silicon image sensor for X-ray diagnostic medical imaging applications. Proceedings of the SPIE 3336: 444-452.
- Hara T, Yamaguchi N, Fujikawa C, Okasaka K, Ohchi T, et al. (1999) Study on tabletop X-ray lasers pumped by a pulse-train laser. In: X-Ray Lasers 1998. Kato Y, Takuma H, Daido H, (Ed.). Bristol, Iop Publishing Ltd. 159: 203-209.
- Rivers ML, Sutton SR, Eng P (1999) Geoscience applications of x-ray computed microtomography. Proceedings of the SPIE 3772: 78-86.
- Paulus MJ, Sari-Sarraf H, Gleason SS, Bobrek M, Hicks JS, et al. (1999) A new X-ray computed tomography system for laboratory mouse imaging. IEEE Transactions on Nuclear Science 46: 558-564.
- Paulus MJ, Gleason SS, Kennel SJ, Hunsicker PR, Johnson DK (2000) High resolution X-ray computed tomography: an emerging tool for small animal cancer research. Neoplasia 2: 62-70.
- Siewerdsen JH, Jaffray DA (2000) Optimization of x-ray imaging geometry (with specific application to flat-panel cone-beam computed tomography). Medical Physics 27: 1903-1914.
- Takeuchi A, Uesugi K, Suzuki Y, Aoki S (2001) Hard X-ray microtomography using X-ray imaging optics. Japanese Journal of Applied Physics Part 1-Regular Papers Short Notes & Review Papers 40: 1499-1503.
- Garcia-Ramirez JL, Mutic S, Dempsey JF, Low DA, Purdy JA (2002) Performance evaluation of an 85-cm-bore x-ray computed tomography scanner designed for radiation oncology and comparison with current diagnostic CT scanners. International Journal of Radiation Oncology Biology Physics 52: 1123-1131: #Pii s0360-3016(01)02779-1.
- Lee SC, Kim HK, Chun IK, Cho MH, Lee SY, et al. (2003) A flat-panel detector based micro-CT system: performance evaluation for small-animal imaging. Physics in Medicine and Biology 48: 4173-4185.
- Kim CH (2004) A Study of an Areas X-Ray Source for Diffraction Enhanced Imaging for Clinical and Industrial Applications [MS Thesis]. Raleigh, North Carolina, USA, Department of Nuclear Engineering, North Carolina State University.
- Goertzen AL, Nagarkar V, Street RA, Paulus MJ, Boone JM, et al. (2004) A comparison of x-ray detectors for mouse CT imaging. Physics in Medicine and Biology 49: 5251-5265.
- Fahrig R, Ganguly A, Starman JD, Strobel N (2004) C-arm CT with XRIIs and digital flat panels: a review. Proceedings of the SPIE 5535: 400-409.
- Sawant A, Antonuk LE, El-Mohri Y, Zhao QH, Li YX, et al. (2005) Segmented crystalline scintillators: An initial investigation of high quantum efficiency detectors for megavoltage x-ray imaging. Medical Physics 32(10): 3067-3083.
- Hoheisel M (2006) Review of medical imaging with emphasis on X-ray detectors. Nuclear Instruments & Methods in Physics Research Section a-Accelerators Spectrometers Detectors and Associated Equipment 563: 215-224.
- Liu Z, Yang G, Lee YZ, Bordelon D, Lu J, et al. (2006) Carbon nanotube based microfocus field emission x-ray source for microcomputed tomography. Applied Physics Letters 89: #103111.
2021 Copyright OAT. All rights reserv
- Boyce SJ, Samei E (2006) Imaging properties of digital magnification radiography. Medical Physics 33: 984-996.
- Stampanoni M, Groso A, Borchert G, Abela R (2007) Bragg magnifier: High-efficiency, high-resolution X-ray detector. In: Synchrotron Radiation Instrumentation, Pts 1 and 2. Choi JY, Rah S, (Ed.). 879: 1168-1171.
- Panetta D, Belcari N, Baldazzi G, Carpentieri C, Cicalini E, et al. (2007) Characterization of a high-resolution CT scanner prototype for small animals. Nuovo Cimento Della Societa Italiana Di Fisica B-General Physics Relativity Astronomy and Mathematical Physics and Methods 122: 739-747.
- Kalender WA, Kyriakou Y (2007) Flat-detector computed tomography (FD-CT). Eur Radiol 17: 2767-2779. [crossref]
- Yang K, Kwan ALC, Boone JM (2007) Computer modeling of the spatial resolution properties of a dedicated breast CT system. Medical Physics 34: 2059-2069.
- Lai CJ, Shaw CC, Chen L, Altunbas MC, Liu X, et al. (2007) Visibility of microcalcification in cone beam breast CT: effects of X-ray tube voltage and radiation dose. Med Phys 34: 2995-3004. [crossref]
- Salamon M, Hanke R, Krueger P, Sukowski F, Uhlmann N, Voland V (2008) Comparison of different methods for determining the size of a focal spot of microfocus X-ray tubes. Nuclear Instruments & Methods in Physics Research Section A-Accelerators Spectrometers Detectors and Associated Equipment 591: 54-58.
- Petin VK, Shljakhtun SV, Oreshkin VI, Ratakhin NA (2008) X-ray source for irradiation of large-area objects. Technical Physics 53: 776-782.
- Sasov A, Liu X, Salmon PL (2008) Compensation of mechanical inaccuracies in micro-CT and nano-CT. Proceedings of the SPIE 7078: #70781c.
- Brunke O, Brockdorf K, Drews S, Müller B, Donath T, Herzen J, Beckmann F (2008) Comparison between X-ray tube based and synchrotron radiation based µCT. Proceedings of the SPIE 7078: #70780u.
- Fahrig R, Ganguly A, Lillaney P, Bracken J, Rowlands JA, Wen Z, Yu H, Rieke V, Santos JM, Pauly KB, Sze DY, Frisoli JK, Daniel BL, Pelc NJ (2008) Design, performance, and applications of a hybrid X-Ray/MR system for interventional guidance. Proceedings of the IEEE 96: 468-480.
- Schlomka J, Roessl E, Dorscheid R, Dill S, Martens G, et al. (2008) Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography. Physics in Medicine and Biology 53: 4031.
- Adam JF, Bayat S, Porra L, Elleaume H, Estève F, et al. (2009) Quantitative functional imaging and kinetic studies with high-Z contrast agents using synchrotron radiation computed tomography. Clinical and Experimental Pharmacology and Physiology 36: 95-106.
- Siemens ME, Li Q, Yang R, Nelson KA, Anderson EH, et al. (2010) Quasi-ballistic thermal transport from nanoscale interfaces observed using ultrafast coherent soft X-ray beams. Nature Materials 9: 26-30.
- Sasov A, Pauwels B, Bruyndonckx P (2010) New type of x-ray source for lensless laboratory nano-CT with 50nm resolution. Proceedings of the SPIE 7804: #78040q.
- Dierolf M, Menzel A, Thibault P, Schneider P, Kewish CM, et al. (2010) Ptychographic X-ray computed tomography at the nanoscale. Nature 467: 436-439. [crossref]
- Oliveira Jr. PD, Vieira MAC, Schiabel H (2010) Determination of focal spot size and the modulation transfer function of mammographic equipment without previous alignment. In: World Congress on Medical Physics and Biomedical Engineering, Vol 25, Pt 4: Image Processing, Biosignal Processing, Modelling and Simulation, Biomechanics. Dossel O, Schlegel WC, (Ed.): 1186-1189.
- Roessl E, Cormode D, Brendel B, Jürgen Engel K, Martens G, Thran A, Fayad Z, Proksa R (2011) Preclinical spectral computed tomography of gold nano-particles. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 648, Supplement 1: S259-S264.
- Xu X, Kim J, Laganis P, Schulze D, Liang Y, et al. (2011) A tetrahedron beam computed tomography benchtop system with a multiple pixel field emission x-ray tube. Medical Physics 38: 5500-5508.
- Popmintchev T, Chen M-C, Popmintchev D, Arpin P, Brown S, et al. (2012) Bright coherent ultrahigh harmonics in the keV x-ray regime from mid-infrared femtosecond lasers. Science 336: 1287-1291.
- Jung JW, Lee JS, Kwon N, Park SJ, Chang S, et al. (2012) Fast microtomography using bright monochromatic x-rays. Review of Scientific Instruments 83: #093704.
- Johnston SM1, Johnson GA, Badea CT (2012) Temporal and spectral imaging with micro-CT. Med Phys 39: 4943-4958. [crossref]
- Qian X, Tucker A, Gidcumb E, Shan J, Yang G, et al. (2012) High resolution stationary digital breast tomosynthesis using distributed carbon nanotube x-ray source array. Medical Physics 39: 2090-2099.
- Filip V, Filip LD, Okuyama F (2013) Miniature x-ray tubes: current state and future prospects. Journal of Instrumentation 8: T03005: #T03005.
- Eaton MF, More M, Chalamala B (2013) Digitally addressable X-ray source for creating X-ray radiation for e.g. medical radiation therapies application, has flat cathode array plate and flat metallic anode plate for forming major integral parts of vacuum enclosure of source [US Patent WO2011044199 A1], Stellarray Inc.
- Sechopoulos I (2013) A review of breast tomosynthesis. Part I. The image acquisition process. Med Phys 40: 014301. [crossref]
- van de Haar P, Ruijters D, Timmer J (2013) Metal artifact reduction in flat-detector CT acquisitions of stent-assisted coiled intracranial aneurysms. (Ed.), European Congress of Radiology 2013: http://posterng.netkey.at/esr/viewing/index.php?module=viewing_poster&pi=118004.
- Kim J, Guan H, Gersten D, Zhang T (2013) Evaluation of algebraic iterative image reconstruction methods for tetrahedron beam computed tomography systems. International Journal of Biomedical Imaging 2013: #609704.
- Kim J, Ionascu D, Zhang T (2013) Technical Note: Algebraic iterative image reconstruction using a cylindrical image grid for tetrahedron beam computed tomography. Medical Physics 40: #081909.
- Gidcumb E, Gao B, Shan J, Inscoe C, Lu J, et al. (2014) Carbon nanotube electron field emitters for x-ray imaging of human breast cancer. Nanotechnology 25: #245704.
- Baldwin Z, Fitchew R (2014) The influence of focal spot size, shape, emission profile and position on field coverage in a Gulmay D3300 Kilovoltage X-ray therapy unit. Australasian Physical & Engineering Sciences in Medicine 37: 515-523.
- Clark DP, Badea CT2 (2014) Micro-CT of rodents: state-of-the-art and future perspectives. Phys Med 30: 619-634. [crossref]
- Sakao T, Narukage N, Suematsu Y, Watanabe K, Shimojo M, et al. (2014) The soft x-ray photon-counting telescope for solar observations. Proceedings of the SPIE 9144: #91443D.
- Rueckel J, Stockmar M, Pfeiffer F, Herzen J (2014) Spatial resolution characterization of a x-ray microCT system. Applied Radiation and Isotopes 94: 230-234.
- Schwoebel PR, Boone JM, Shao J (2014) Studies of a prototype linear stationary x-ray source for tomosynthesis imaging. Phys Med Biol 59: 2393-2413. [crossref]
- Hofmann C, Knaup M, Kachelrieß M (2014) Effects of ray profile modeling on resolution recovery in clinical CT. Med Phys 41: 021907. [crossref]
- Kim J, Lu W, Zhang T (2014) Dual source and dual detector arrays tetrahedron beam computed tomography for image guided radiotherapy. Physics in Medicine and Biology 59: 615-630.
- Popmintchev D, Hernandez-Garcia C, Dollar F, Mancuso C, Perez-Hernandez JA, et al. (2015) Ultraviolet surprise: Efficient soft x-ray high-harmonic generation in multiply ionized plasmas. Science 350: 1225-1231.
- GE Measurement & Control (2015) ERESCO MF4: Reliable, Lightweight, Portable X-ray Generator, General Electric.
- Shan J, Tucker AW, Gaalaas LR, Wu G, Platin E, et al. (2015) Stationary intraoral digital tomosynthesis using a carbon nanotube X-ray source array. Dentomaxillofacial Radiology 44: #20150098.
- Dudak J, Zemlicka J, Krejci F, Karch J, Patzelt M, et al. (2016) Evaluation of sample holders designed for long-lasting X-ray micro-tomographic scans of ex-vivo soft tissue samples. Journal of Instrumentation 11: C03005: #C03005.
- Dudak J, Zemlicka J, Krejci F, Polansky S, Jakubek J, et al. (2015) X-ray micro-CT scanner for small animal imaging based on Timepix detector technology. Nuclear Instruments & Methods in Physics Research Section a-Accelerators Spectrometers Detectors and Associated Equipment 773: 81-86.
- Industrial Imaging Solutions (2016) Replacement X-Ray Tubes and Cables. http://solutionsinimaging.com/product-solutions/
- COMET Technologies (2016) High-Power Technology X-Ray Tubes: Delivering more x-ray light from ever decreasing focal spot sizes. http://www.comet-xray.com/Technology-en/High-Power
- COMET Technologies (2016) X-Ray Tube MXR-321. http://www.comet-xray.com/Products/X-Ray-Tubes/MXR-321
- Gulmay (2016) Bipolar 320KV X-Ray Tubes. http://www.gulmay.com/x-ray-tubes/bipolar-320kv-x-ray-tubes/
- Varian Medical Systems (2016) NDI-321 Stationary Anode X-Ray Tube. https://www.varian.com/media/101127/browser
- Zhang PF, Sun JF, Sun FJ, Qiu AC, Sun J, et al. (2016) Simulation analysis of a pulsed compact FLTD system for large-area hard x-ray sources. IEEE Transactions on Plasma Science 44: 803-807.
- Ogurreck M, Greving I, Marschall F, Vogt H, Last A, et al. (2016) Layout and first results of the nanotomography endstation at the P05 beamline at PETRA III. AIP Conference Proceedings, XRM 2014: Proceedings of the 12th International Conference on X-Ray Microscopy 1696: #020008.
- Hedayat A, Nagy N, Packota G, Monteith J, Allen D, et al. (2016) Synchrotron-radiation-based X-ray micro-computed tomography reveals dental bur debris under dental composite restorations. Journal of Synchrotron Radiation 23: 777-782.
- Koksel F, Aritan S, Strybulevych A, Page JH, Scanlon MG (2016) The bubble size distribution and its evolution in non-yeasted wheat flour doughs investigated by synchrotron X-ray microtomography. Food Research International 80: 12-18.
- Shein EV, Skvortsova EB, Dembovetskii AV, Abrosimov KN, Il'in LI, et al. (2016) Pore-size distribution in loamy soils: A comparison between microtomographic and capillarimetric determination methods. Eurasian Soil Science 49: 315-325.
- Bruker (2016) SkyScan 1172: High resolution desk-top micro-CT. http://bruker-microct.com/products/1172.htm
- Xu J, Sisniega A, Zbijewski W, Dang H, Stayman JW, et al. (2016) Modeling and design of a cone-beam CT head scanner using task-based imaging performance optimization. Physics in Medicine and Biology 61: 3180-3207.
- Zamir A, Arthurs OJ, Hagen CK, Diemoz PC, Brochard T, et al. (2016) X-ray phase contrast tomography; proof of principle for post-mortem imaging. British Journal of Radiology 89: #20150565.
- Gong H, Liu R, Yu H, Lu J, Zhou O, et al. (2016) Interior tomographic imaging of mouse heart in a carbon nanotube micro-CT. Journal of X-Ray Science and Technology 24: 549-563.
- Kasinski K, Maj P, Grybos P, Koziol A (2016) Hardware solutions for the 65k pixel X-ray camera module of 75 mu m pixel size. Journal of Instrumentation 11: C01060: #C01060.
- Gkoumas S, Wang ZT, Abis M, Arboleda C, Tudosie G, et al. (2016) Grating-based interferometry and hybrid photon counting detectors: Towards a new era in X-ray medical imaging. Nuclear Instruments & Methods in Physics Research Section A-Accelerators Spectrometers Detectors and Associated Equipment 809: 23-30.
- Ghani MU, Zhou ZX, Ren LQ, Wong M, Li YH, et al. (2016) Investigation of spatial resolution characteristics of an in vivo microcomputed tomography system. Nuclear Instruments & Methods in Physics Research Section A-Accelerators Spectrometers Detectors and Associated Equipment 807: 129-136.
- Zhao W, Vernekohl D, Zhu J, Wang L, Xing L (2016) A model-based scatter artifacts correction for cone beam CT. Med Phys 43: 1736. [crossref]
- Fila T, Kumpová I, Koudelka P, Zlámal P, Vavrík D, et al. (2016) Dual-energy X-ray micro-CT imaging of hybrid Ni/Al open-cell foam. Journal of Instrumentation 11: C01005: #C01005.
- Leng S, Yu Z, Halaweish A, Kappler S, Hahn K, et al. (2016) A high-resolution imaging technique using a whole-body, research photon counting detector CT system. Proceedings of the SPIE 9783: doi: 10.1117/1112.2217180.
- Davidi R, Herman GT, Langthaler O, Sardana S, Ye Z (2015) SNARK14: A Programming System for the Reconstruction of 2D Images from 1D Projections: http://www.dig.cs.gc.cuny.edu/software/snark14/.
- Flohr T, Stierstorfer K, Raupach R, Ulzheimer S, Bruder H (2004) Performance evaluation of a 64-slice CT system with z-flying focal spot. Rofo 176: 1803-1810. [crossref]
- Grimes J, Duan X, Yu L, Halaweish AF, Haag N, Leng S, McCollough C (2015) The influence of focal spot blooming on high-contrast spatial resolution in CT imaging. Medical Physics 42: 6011-6020.
- Rickard MT (1989) The quality mammographic image. A review of its components. Australasian Radiology 33: 328-334.
- Grider DE, Wright A, Ausburn PK (1986) Electron beam melting in microfocus x-ray tubes. Journal of Physics D-Applied Physics 19: 2281-2292.
- Sterpin E, Chen Y, Lu W, Mackie TR, Olivera GH, et al. (2011) On the relationships between electron spot size, focal spot size, and virtual source position in Monte Carlo simulations. Medical Physics 38: 1579-1586.
- Oxford Instruments (2016) X-ray Tubes and Power Supplies. https://www.oxford-instruments.com/products/x-ray-tubes-and-integrated-sources/x-ray-tubes
- Varian Medical Systems (2016) NDT Security. https://www.varian.com/x-ray-imaging-components/products/security-industrial-imaging/industrial-tubes/ndt-security
- Iversen AH, Whitaker S (1984) A new high heat load x-ray tube. Proceedings of the SPIE 454: 304-310.
- Webber RL, Ed. (1979) Feedback Control of Exposure Geometry in Dental Radiography [Publ. No. 80-1954]. Bethesda, U.S. National Institutes of Health.
- Gordon R (1979) Feedback control of exposure geometry in dental radiography workshop, University of Connecticut, 16 May 1978. Applied Optics 18: 1769, 1834.
- Alvare G, Gordon R (2015) CT Brush and CancerZap!: two video games for computed tomography dose minimization. Theoretical Biology and Medical Modelling 12: #7.
- Sun XP, Liu ZG, Sun TX, Yi LT, Sun WY, et al. (2015) Application of polycapillary x ray lens to eliminate both the effect of x ray source size and scatter of the sample in laboratory tomography. Chinese Optics Letters 13: #093401.
- Schields PJ, Gibson DM, Gibson WM, Gao N, Huang HP, et al. (2002) Overview of polycapillary X-ray optics. Powder Diffraction 17: 70-80.
- Jorgensen SM, Reyes DA, MacDonald CA, Ritman EL (1999) Micro-CT scanner with a focusing polycapillary x-ray optic. Proceedings of the SPIE 3772: 158-166.
- Lehr J (1997) 3D X-ray microscopy: Tomographic imaging of mineral sheaths of bacteria Leptothrix Ochracea with the Gottingen x-ray microscope at BESSY. Optik 104: 166-170.
- Gorham S, Brennan PC (2010) Impact of focal spot size on radiologic image quality: A visual grading analysis. Radiography 16: 304-313.
- Law J, Robinson A, Underwood AC (1996) Focal spot sizes in dual-track Mo and Rh target mammographic X-ray tubes. Br J Radiol 69: 1077-1078. [crossref]
- Xu J (2014) Modeling and Development of Iterative Reconstruction Algorithms in Emerging X-ray Imaging Technologies [Ph.D. Thesis]. St. Louis, Department of Biomedical Engineering, Washington University in St. Louis.
- Colquhoun GD, Gordon R, Elbakri IA (2004) Reversed cone beam coded aperture mammography [Abstract 4408744, rejected]. In: Radiological Society of North America 2004 Scientific Assembly and Annual Meeting(Ed.): Poster.
- Pan X, Yu L, Kao CM (2005) Spatial-resolution enhancement in computed tomography. IEEE Trans Med Imaging 24: 246-253. [crossref]
- Létang JM, Peix G (2003) On-line X-ray focal spot assessment based on deconvolution using standard imaging devices. NDT & E International 36: 303-317.
- Taylor T, Reynolds PW (1985) Spatial response of source–collimator–detector systems for industrial applications of computed tomography. Applied Optics 24: 4064-4066.
- Verly JG (1981) Effects of arbitrary focal spot intensity distribution, detector width, and scanning eccentricity in x-ray computed-tomography. IEEE Transactions on Acoustics Speech and Signal Processing 29: 98-106.
- Tilley S, Siewerdsen JH, Stayman JW (2016) Model-based iterative reconstruction for flat-panel cone-beam CT with focal spot blur, detector blur, and correlated noise. Phys Med Biol 61: 296-319. [crossref]
- Verly JG (1980) X-ray computed-tomography in the presence of arbitrary symmetrical focal spot intensity distributions. Medical Physics 7: 27-34.
- Nagesh SVS, Rana R, Russ M, Ionita CN, Bednarek DR, et al. (2016) Focal Spot Deblurring for High Resolution Direct Conversion X-ray Detectors. Proc SPIE Int Soc Opt Eng 9783. [crossref]
- Yu H, Wang G (2012) Finite detector based projection model for high spatial resolution. J Xray Sci Technol 20: 229-238. [crossref]
- Gordon R (1974) A tutorial on ART (Algebraic Reconstruction Techniques) [Erratum in Eq. 18: max, not min]. IEEE Transactions on Nuclear Science NS-21: 78-93, 95.
- Gordon R, Herman GT (1974) Three-dimensional reconstruction from projections: a review of algorithms. International Review of Cytology 38: 111-151.
- Browne JA, Boone JM, Holmes TJ (1995) Maximum-likelihood x-ray computed-tomography finite-beamwidth considerations. Applied Optics 34: 5199-5209.
- Nuyts J, De Man B, Fessler JA, Zbijewski W, Beekman FJ (2013) Modelling the physics in the iterative reconstruction for transmission computed tomography. Physics in Medicine and Biology 58: R63-R96.
- Hofmann C, Knaup M, Kachelrieß M (2013) Do we need to model the ray profile in iterative clinical CT image reconstruction? [SSE23-05]. In: Radiological Society of North America 2013 Scientific Assembly and Annual Meeting(Ed.): http://rsna2013.rsna.org/program/details/?emID=13013675.
- Fu L, Wang J, Rui X, Thibault JB, De Man B (2013) Modeling and estimation of detector response and focal spot profile for high-resolution iterative CT reconstruction. In: 2013 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC)(Ed.): doi: 10.1109/NSSMIC.2013.6829044.
- Do S, Karl WC, Singh S, Kalra M, Brady T, et al. (2014) High fidelity system modeling for high quality image reconstruction in clinical CT. PLoS One 9: e111625. [crossref]
- Chang M, Xiao YS, Chen ZQ (2014) Improve spatial resolution by Modeling Finite Focal Spot (MFFS) for industrial CT reconstruction. Optics Express 22: 30641-30656.
- Fluke Biomedical (2016) X-Ray Pinhole Assemblies. http://www.flukebiomedical.com/biomedical/usen/diagnostic-imaging-qa/x-ray-qa-instruments/07-611-to-07-633-x-ray-pinhole-assemblies.htm?PID=54321
- Gazi PM, Yang K, Burkett GW Jr, Aminololama-Shakeri S, Seibert JA, et al. (2015) Evolution of spatial resolution in breast CT at UC Davis. Med Phys 42: 1973-1981. [crossref]
- Nickoloff EL, Donnelly E, Eve L, Atherton JV, Asch T (1990) Mammographic resolution: influence of focal spot intensity distribution and geometry. Medical Physics 17: 436-447.
- Bracken J, Komljenovic P, Green D, DeCrescenzo G (2008) XMR: Fusion of MRI and X-ray modalities. http://sunnybrook.ca/research/content/?page=sri-groups-xray-proj-9
- Bracken JA, Komljenovic P, Lillaney PV, Fahrig R, Rowlands JA (2009) Closed-bore XMR (CBXMR) systems for aortic valve replacement: X-ray tube imaging performance. Medical Physics 36: 1086-1097.
- Katz MC, Nickoloff EL (1992) Radiographic detail and variation of the nominal focal spot size: the "focal effect". RadioGraphics 12: 753-761.
- Geldner E, Schnitger H (1982) International Electro Technical Commission publication 336 1981 revised edition of the standard for focal spots of x-ray tubes. Electromedica (English Edition) 50: 6-10.
- Kratzat M (1988) Evaluating the importance of focal spot sizes in mammography. Medicamundi 33: 74-80.
- Law J (1993) Measurement of focal spot size in mammography X-ray tubes. Br J Radiol 66: 44-50. [crossref]
- Michielsen K, Van Slambrouck K, Jerebko A, Nuyts J (2013) Patchwork reconstruction with resolution modeling for digital breast tomosynthesis. Medical Physics 40: #031105.
- Kingston AM, Sakellariou A, Sheppard AP, Varslot TK, Latham SJ (2010) An auto-focus method for generating sharp 3D tomographic images. Proceedings of the SPIE 7804: #78040j.
- Kubota H, Ozaki Y, Matsumoto M, Kanamori H (1993) Determination of x-ray tube focal spot position. Med Phys 20: 1029-1031. [crossref]
- Nagesh SS, Rana R, Russ M, Ionita C, Bednarek D, Rudin S (2015) Focal spot deblurring for high resolution amorphous selenium (aSe) complementary metal oxide semiconductor (CMOS) x-ray detector. Medical Physics 42: 3694.
- Zeng K, De Man B, Thibault JB, Yu Z, Bouman C, et al. (2009) Spatial resolution enhancement in CT iterative reconstruction. In: 2009 IEEE Nuclear Science Symposium Conference Record, Vols 1-5. Yu B, (Ed.): 3748-3751.
- Mazur EJ, Gordon R (1995) Interpolative algebraic reconstruction techniques without beam partitioning for computed tomography. Medical & Biological Engineering & Computing 33: 82-86.
- Bernstein H, Bergeron RT, Klein DJ (1974) The relationship of the radiant intensity distribution of focal spots to resolution. Radiology 111: 427-431.
- Kruger DG, Abreu CC, Hendee EG, Kocharian A, Peppler WW, et al. (1996) Imaging characteristics of x-ray capillary optics in digital mammography. Medical Physics 23: 187-196.
- Bradford CD, Peppler WW, Ross RE (2002) Multitapered x-ray capillary optics for mammography. Med Phys 29: 1097-1108. [crossref]
- Chen Z, Ning R (2007) Anisotropic point spread function of cone-beam computed tomography. Proceedings of the SPIE 6510: U157-U168.
- Fritz SL, Livingston WH (1982) A comparison of computed and measured heel effect for various target angles. Med Phys 9: 216-219. [crossref]
- Whiting BR, Evans JD, Dohatcu AC, Williamson JF, Politte DG (2014) Measurement of bow tie profiles in CT scanners using a real-time dosimeter. Medical Physics 41: #101915.
- Spitzer V, Ackerman MJ, Scherzinger AL, Whitlock D (1996) The visible human male: A technical report. Journal of the American Medical Informatics Association 3: 118-130.
- Yoo TS (2016) The Visible Human Project, U.S. National Library of Medicine. https://lhncbc.nlm.nih.gov/project/visible-human-project
- Compositor (2016) Compositor. http://www.artlythere.com/Compositor.html
- Taschetta-Millane M, Fornell D, Zagoudis J (2015) Computed Tomography Systems: Comparison Chart. http://www.itnonline.com/content/computed-tomography-systems
- Schultz E, Felix R (1980) Fan-beam computerized tomography systems with rotating and with stationary detector arrays ('third' and 'fourth' generation). Medical Progress through Technology 7: 169-181.
- Robb RA (1982) X-ray computed tomography: an engineering synthesis of multiscientific principles. CRC Critical Reviews in Biomedical Engineering 7: 265-333.
- Gordon R, Bender R, Herman GT (1970) Algebraic Reconstruction Techniques (ART) for three-dimensional electron microscopy and x-ray photography. Journal of Theoretical Biology 29: 471-481.
- Lent A (1977) A convergent algorithm for maximum entropy image restoration, with a medical x-ray application. In: Image Analysis and Evaluation: SPSE Conference Proceedings, July 19-23, 1976, Toronto, Canada. Shaw R, (Ed.). Washington, DC, USA, Society of Photographic Scientists and Engineers: 249-257.
- Das SK, Shukla AK (2011) Two-dimensional ionospheric tomography over the low-latitude Indian region: An intercomparison of ART and MART algorithms. Radio Science 46: #Rs2005.
- Donaire JG, García I (2002) On using global optimization to obtain a better performance of a MART algorithm in 3D x-ray tomography. Journal of Imaging Science and Technology 46: 247-256.
- Mishra D, Muralidhar K, Munshi P (1999) A robust MART algorithm for tomographic applications. Numerical Heat Transfer Part B-Fundamentals 35: 485-506.
- Colquhoun GD, Gordon R (2005) The use of control angles with MART (Multiplicative Algebraic Reconstruction Technique). Technology in Cancer Research and Treatment 4: 183-184.
- Badea C, Gordon R (2004) Experiments with the nonlinear and chaotic behaviour of the multiplicative algebraic reconstruction technique (MART) algorithm for computed tomography. Physics in Medicine and Biology 49: 1455-1474.
- Mailloux GE, Mallouche H, Noumeir R, Lemieux R (1993) The MART algorithm for SPECT and entropy maximization. Proceedings of the SPIE 1887: 40-49.
- Lent A, Censor Y (1991) The primal-dual algorithm as a constraint-set-manipulation device. Mathematical Programming 50: 343-357.
- Dusaussoy NJ, Abdou IE (1991) The extended MENT algorithm: a maximum-entropy type algorithm using prior knowledge for computerized-tomography. IEEE Transactions on Signal Processing 39: 1164-1180.
- Yoshinaga T, Imakura Y, Fujimoto K, Tetsushi U (2008) Bifurcation analysis of iterative image reconstruction method for computed tomography. International Journal of Bifurcation and Chaos 18: 1219-1225.
- Wikipedia (2016) Kaczmarz method. https://en.wikipedia.org/wiki/Kaczmarz_method
- Maass C, Knaup M, Kachelriess M (2011) New approaches to region of interest computed tomography. Med Phys 38: 2868-2878. [crossref]
- Chaudhuri BB, Rosenfeld A (1998) On the computation of the digital convex hull and circular hull of a digital region. Pattern Recognition 31: 2007-2016.
- Beyer WA, Ulam SM (1968) Note on the visual hull of a set. Journal of Combinatorial Theory 4: 240-245.
- Meisters GH, Ulam SM (1967) On visual hulls of sets. Proceedings of the National Academy of Sciences USA 57: 1172-1174.
- Gordon R, Rangaraj MR (1982) Experiments on streak prevention in image reconstruction from a few views. In: Proceedings of the 4th Biennial Conference of the Canadian Society for Computational Studies of Intelligence, University of Saskatchewan, Saskatoon, Saskatchewan, 17-19 May 1982(Ed.). Toronto, Canadian Society for Computational Studies of Intelligence: 41-47.
- Rangayyan RM, Gordon R (1982) Streak Preventive Image Reconstruction with ART and Adaptive Filtering. IEEE Trans Med Imaging 1: 173-178. [crossref]
- Wang G, Snyder DL, O'Sullivan JA, Vannier MW (1996) Iterative deblurring for CT metal artifact reduction. IEEE Trans Med Imaging 15: 657-664. [crossref]
- Dhawan AP, Rangayyan RM, Gordon R (1984) Wiener filtering for deconvolution of geometric artifacts in limited-view image reconstruction. Proceedings of the SPIE 515: 168-172.
- Gordon R (1973) Artifacts in reconstructions made from a few projections. In: Proceedings of the First International Joint Conference on Pattern Recognition, Oct. 30 to Nov. 1, 1973, Washington, D. C. Fu KS, (Ed.). Northridge, California, IEEE Computer Society: 275-285.
- Jomier J, Rit S, Oliva MV (2013) RTK: The Reconstruction Toolkit. http://www.kitware.com/source/home/post/115
- Wang Y, Tsui BMW (2007) Pinhole SPECT with different data acquisition geometries: Usefulness of unified projection operators in homogeneous coordinates. IEEE Transactions on Medical Imaging 26: 298-308.
- Bhagtani R, Schmidt TG (2009) Simulated scatter performance of an inverse-geometry dedicated breast CT system. Medical Physics 36: 788-796.
- Schmidt TG, Fahrig R, Pelc NJ (2005) A three-dimensional reconstruction algorithm for an inverse-geometry volumetric CT system. Medical Physics 32: 3234-3245.
- Mazin S, Star-Lack J, Schmidt TG, Pelc NJ (2005) 2D simulations of an inverse-geometry volumetric CT system with multiple detector arrays. Proceedings of the SPIE 5745: 889-897.
- Brehm M, Paysan P, Oelhafen M, Kachelrieß M (2013) Artifact-resistant motion estimation with a patient-specific artifact model for motion-compensated cone-beam CT. Medical Physics 40: #101913.
- Braun H, Kyriakou Y, Kachelriss M, Kalender WA (2010) The influence of the heel effect in cone-beam computed tomography: artifacts in standard and novel geometries and their correction. Physics in Medicine and Biology 55: 6005-6021.
- Wu XL (1991) An efficient antialiasing technique. SIGGRAPH 91 Conference Proceedings 25: 143-152.
- Mueller K, Yagel R, Wheller JJ (1999) Fast implementations of algebraic methods for three-dimensional reconstruction from cone-beam data. IEEE Trans Med Imaging 18: 538-548. [crossref]
- Siddon RL (1985) Fast calculation of the exact radiological path for a three-dimensional CT array. Medical Physics 12: 252-255.
- Joseph PM (1982) An improved algorithm for reprojecting rays through pixel images. IEEE Transactions on Medical Imaging 1: 192-196.
- Schretter C (2006) A fast tube of response ray-tracer. Med Phys 33: 4744-4748. [crossref]
- Gilbert P (1972) Iterative methods for the three-dimensional reconstruction of an object from projections. Journal of Theoretical Biology 36: 105-117.
- Fager RS, Peddanarappagari KV, Kumar GN (1993) Pixel-based reconstruction (PBR) promising simultaneous techniques for ct reconstructions. IEEE Transactions on Medical Imaging 12: 4-9.
- Jaman KA, Gordon R, Rangayyan RM (1985) Display of 3D anisotropic images from limited-view computed tomograms. Computer Vision, Graphics, Image Processing 30: 345-361.
- Guan H, Gordon R (1994) A projection access order for speedy convergence of ART (Algebraic Reconstruction Technique): a multilevel scheme for computed tomography. Physics in Medicine and Biology 39: 2005-2022.
- Guan H, Gordon R (1996) Computed tomography using Algebraic Reconstruction Techniques (ARTs) with different projection access schemes: a comparison study under practical situations. Physics in Medicine and Biology 41: 1727-1743.
- Guan H, Gordon R, Zhu Y (1998) Combining various projection access schemes with the Algebraic Reconstruction Technique for low-contrast detection in computed tomography. Physics in Medicine and Biology 43: 2413-2421.
- Jiang X, Guan H, Gordon R (1992) Contrast enhancement using "feature pixels" or "fixels" for pixel-independent image processing. Radiology 185(Suppl.): 391.
- Peng R, Zhang J, Calderon-Colon X, Wang S, Sultana S, et al. (2010) Design, optimization and testing of a multi-beam micro-CT scanner based on multi-beam field emission x-ray technology. Proceedings of the SPIE 7622: #76221g.
- Wikipedia (2016) Bresenham's line algorithm. https://en.wikipedia.org/wiki/Bresenham%27s_line_algorithm
- Ziegler A, Nielsen T, Grass M (2008) Iterative reconstruction of a region of interest for transmission tomography. Medical Physics 35: 1317-1327.
- Faridani A, Ritman EL, Smith KT (1992) Local Tomography. SIAM Journal on Applied Mathematics 52: 459-484.
- Hutchinson J (2001) Culture, communication, and an information age madonna. IEEE Professional Communication Society Newsletter 45: 1-7.
- Hooker D (1972) Lena Söderberg. Playboy Magazine 19: centerfold.
- Van Tassel J (1996) The legend of Lena: image processing's main squeeze. Advanced Imaging 11: 56-60.
- Ye IB, Wang G (2012) Tetrahedron-based orthogonal simultaneous scan for cone-beam computed tomography. Optical Engineering 51: #080502.
- Wikipedia (2015) John von Neumann. http://en.wikipedia.org/wiki/John_von_Neumann
- Busta H, Lesiak S (2006) Decontamination and sterilization system using large area x-ray source [US Patent Application Publication US 2006/0049359 A1]. Washington, DC, USA, US Patent Office.
- Eaton M (2015) Modular Addressable Research Irradiator using Flat Panel X-ray Sources. https://www.sbir.gov/node/968061
- Comish C (2014) Stellarray Wins $1.1 Million Grant for Blood Safety Device to Replace Cesium 137. https://bionews-tx.com/news/2014/03/12/stellarray-wins-1-1-million-grant-for-blood-safety-device-to-replace-cesium-137/
- Malglaive F, Albert RD (2009) Reverse geometry X-ray imaging. Insight 51: 66-68.
- Bellman SH, Bender R, Gordon R, Rowe Jr JE (1971) ART is science, being a defense of Algebraic Reconstruction Techniques for three-dimensional electron microscopy. Journal of Theoretical Biology 32: 205-216.
- Dhawan AP, Rangayyan RM, Gordon R (1985) Image restoration by Wiener deconvolution in limited-view computed tomography. Appl Opt 24: 4013. [crossref]
- Arroyo F, Arroyo E, Li X, Zhu J (2013) Numerical studies of the generalized l1 greedy algorithm for sparse signals. Advances in Computed Tomography 2: 132-139.
- Li X, Wang H, Wu Y, Zhu J (2011) A full row-rank system matrix generated along two directions in discrete tomography. Applied Mathematics and Computation 218: 107-114.
- Zhu JH, Li XZ (2013) A generalized l1 greedy algorithm for image reconstruction in CT. Applied Mathematics and Computation 219: 5487-5494.
- Li X, Zhu J (2010) Convergence of block cyclic projection and Cimmino algorithms for compressed sensing based tomography. Journal of X-Ray Science and Technology 18: 369-379.
- Graff CG, Sidky EY (2015) Compressive sensing in medical imaging. Appl Opt 54: C23-44. [crossref]
- Van de Sompel D, Brady SM, Boone J (2011) Task-based performance analysis of FBP, SART and ML for digital breast tomosynthesis using signal CNR and Channelised Hotelling Observers. Medical Image Analysis 15: 53-70.
- Bian J, Han X, Yang K, Sidky EY, Boone JM, et al. (2012) A preliminary investigation of reduced-view image reconstruction from low-dose breast CT data. Proceedings of the SPIE 8313: #831325.
- Gordon R (1985) Toward robotic x-ray vision: new directions for computed tomography. Applied Optics 24: 4124-4133.
- Lell MM, Wildberger JE, Alkadhi H, Damilakis J, Kachelriess M (2015) Evolution in Computed Tomography: The Battle for Speed and Dose. Invest Radiol 50: 629-644. [crossref]
- Moore GE (1965) Cramming more components onto integrated circuits. Electronics 38: 114-117.
- Wikipedia (2016) Moore's law. https://en.wikipedia.org/wiki/Moore%27s_law
- Sharov AA, Gordon R (2017) Life before Earth. In: Habitability of the Universe Before Earth [in series: Astrobiology: Exploring Life on Earth and Beyond, eds. Pabulo Henrique Rampelott, Joseph Seckbach & Richard Gordon]. Gordon R, Sharov AA, (Ed.). Amsterdam, Elsevier B.V.: In press.
- Sharov AA, Gordon R (2013) Life Before Earth. http://arxiv.org/abs/1304.3381
- Carron I (2012) What is Faster than Moore's Law and Why You Should Care. http://nuit-blanche.blogspot.fr/2012/06/what-is-faster-than-moores-law-and-why.html
- Nielsen IMB, Janssen CL (2000) Multi-threading: A new dimension to massively parallel scientific computation. Computer Physics Communications 128: 238-244.
- Ungerer T, Robic B, Šilc J (2002) Multithreaded processors. Computer Journal 45: 320-348.
- Zenios SA, Censor Y (1991) Parallel computing with block-iterative image reconstruction algorithms. (Ed.): 399-415.
- Fitchett JW (1993) A Locally Synchronous Globally Asynchronous Vertex-8 Processing Element for Image Reconstruction on a Mesh [Masters Thesis]. Winnipeg, Department of Electrical and Computer Engineering, University of Manitoba.
- Gordon R, Herman GT, Johnson SA (1975) Image reconstruction from projections. Scientific American 233: cover, 12, 56-61, 64-68, 139.
- Martin D, Thulasiraman P, Gordon R (2005) Local independence in computed tomography as a basis for parallel computing. Technology in Cancer Research and Treatment 4: 187-188.
- Melvin C, Thulasiraman P, Gordon R (2003) Parallel Algebraic Reconstruction Technique for computed tomography. In: PDPTA'03: Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications, Vols 1-4. Arabnia HR, Mun Y, (Ed.): 532-536.
- Gordon R (1976) Dose reduction in computerized tomography [Guest Editorial]. Investigative Radiology 111: 508-517.
- Di Domenico G, Cardarelli P, Contillo A, Taibi A, Gambaccini M (2016) X-ray focal spot reconstruction by circular penumbra analysis-Application to digital radiography systems. Medical Physics 43: 294-302.







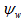 finite elements; 3) large dashes, aw = 5 foxels used in reconstructing the plane of voxels. aw is an independent variable. In our simulation, these three arcs would be superimposed on the ring of detector pixels. They are displaced radially here for clarity. (b): The focal spot is divided into multiple foxels (just aw = 3 here) which project rays onto the detector pixels. For aw = 3 here, the foxels have the same width as the detector pixels. The projections are taken from the midpoints of the foxels. The rays from each foxel are colored differently. Dashes are to make the figure understandable in gray scale. (c): The same rays are recolored according to which detector pixels see them. For each detector pixel, these are the rays, grouped into a compound ray, used to calculate
finite elements; 3) large dashes, aw = 5 foxels used in reconstructing the plane of voxels. aw is an independent variable. In our simulation, these three arcs would be superimposed on the ring of detector pixels. They are displaced radially here for clarity. (b): The focal spot is divided into multiple foxels (just aw = 3 here) which project rays onto the detector pixels. For aw = 3 here, the foxels have the same width as the detector pixels. The projections are taken from the midpoints of the foxels. The rays from each foxel are colored differently. Dashes are to make the figure understandable in gray scale. (c): The same rays are recolored according to which detector pixels see them. For each detector pixel, these are the rays, grouped into a compound ray, used to calculate 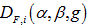 in Equation 2. A similar calculation, emanating from the
in Equation 2. A similar calculation, emanating from the 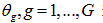 is the angle of the line between the middle of the focal spot and the detector pixel in the middle of the arc of detector pixels encountered by the fan beam of angle
is the angle of the line between the middle of the focal spot and the detector pixel in the middle of the arc of detector pixels encountered by the fan beam of angle 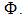 . The length of that line is the diameter 2r of the gantry. This geometry can represent either a third generation CT scanner, in which the arc of detector pixels and the x-ray source rotate together, or a fourth-generation scanner, in which there is a full ring of stationary detector pixels, and only the x-ray source rotates. However, we do constrain both to have equal distances r from the center of rotation in our simulation. The indexing of the detector pixels in the fan beam, a = 1,....amax , depends on which generation scanner is being considered. The index β is needed when the detector array is two dimensional. Our code applies to third generation, though our results are independent of third versus fourth generation. Note that figures similar to (b) and (c) could be drawn for the finite elements, but would involve different rays between the finite elements and the detector pixels
. The length of that line is the diameter 2r of the gantry. This geometry can represent either a third generation CT scanner, in which the arc of detector pixels and the x-ray source rotate together, or a fourth-generation scanner, in which there is a full ring of stationary detector pixels, and only the x-ray source rotates. However, we do constrain both to have equal distances r from the center of rotation in our simulation. The indexing of the detector pixels in the fan beam, a = 1,....amax , depends on which generation scanner is being considered. The index β is needed when the detector array is two dimensional. Our code applies to third generation, though our results are independent of third versus fourth generation. Note that figures similar to (b) and (c) could be drawn for the finite elements, but would involve different rays between the finite elements and the detector pixels



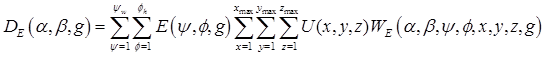 [1]
[1]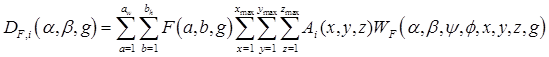 [2]
[2]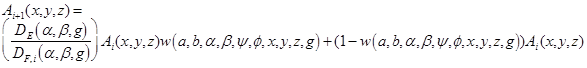 [3]
[3]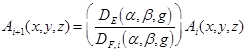 [5]
[5]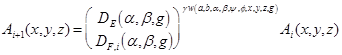 [6]
[6]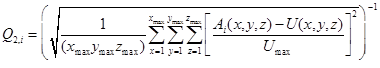 [8]
[8]
 but the calculations can be continued after stopping. A log of all the input and output parameters and the current reconstructed image can be output by the SAVE command. The PLOT shows the voxel values along a horizontal line through the center of the latest reconstructed image. The SHOW command may be used to display the original input image. However, after clicking SHOW, except for the information in the log, the work done so far is lost. RESET IMAGE deletes the work done so far (except for the log text), allowing a start from scratch. It can be useful when comparing the effects of different parameters on a single image. STOP ends the program with the image that is currently displayed on the screen. That image is updated after every iteration, so the progress of the computation can be followed visually. The file name convention for the output we use in this paper is just the parameters in the order shown here, namely “Lena 3 3 3 435 57 1 7 W 1” in this example. Note h = aw. In terms of our equations, the values in the first two input rows correspond to
but the calculations can be continued after stopping. A log of all the input and output parameters and the current reconstructed image can be output by the SAVE command. The PLOT shows the voxel values along a horizontal line through the center of the latest reconstructed image. The SHOW command may be used to display the original input image. However, after clicking SHOW, except for the information in the log, the work done so far is lost. RESET IMAGE deletes the work done so far (except for the log text), allowing a start from scratch. It can be useful when comparing the effects of different parameters on a single image. STOP ends the program with the image that is currently displayed on the screen. That image is updated after every iteration, so the progress of the computation can be followed visually. The file name convention for the output we use in this paper is just the parameters in the order shown here, namely “Lena 3 3 3 435 57 1 7 W 1” in this example. Note h = aw. In terms of our equations, the values in the first two input rows correspond to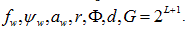

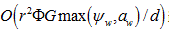 is shown. The proportionality constant is 1.1x10-7 with
is shown. The proportionality constant is 1.1x10-7 with
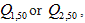 whichever norm is designated. B: T = a 512x512 voxel halftone test pattern “Lena”[
whichever norm is designated. B: T = a 512x512 voxel halftone test pattern “Lena”[

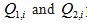 peaked at iteration i = 2. Their values are listed respectively for each iteration. While this is an unlikely set of parameters, with
peaked at iteration i = 2. Their values are listed respectively for each iteration. While this is an unlikely set of parameters, with 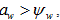 it illustrates that simple image quality measures cannot be used without visually checking on them. B: Checking the images against the graph, we have the counterintuitive conclusion that the visual quality increases while the quantitative quality measures decline. Squares are
it illustrates that simple image quality measures cannot be used without visually checking on them. B: Checking the images against the graph, we have the counterintuitive conclusion that the visual quality increases while the quantitative quality measures decline. Squares are 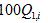 and triangles are
and triangles are 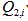 versus iteration i.
versus iteration i.
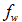 = 21 voxels, reconstructed with aw = 1 foxel. Thus, a wide focal spot is treated as if it were a point source. The number of finite elements
= 21 voxels, reconstructed with aw = 1 foxel. Thus, a wide focal spot is treated as if it were a point source. The number of finite elements 

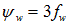 . Images are at 30 iterations. The focal spot width fw is increased in powers of 2, with 1 added to get an odd number, so that the fan beam has a central ray. The number of foxels aw is proportional to the focal spot width. The peak image quality for a focal spot width of fw = 21 was reached with 18 foxels in Figure 17. Here we maintain this ratio:
. Images are at 30 iterations. The focal spot width fw is increased in powers of 2, with 1 added to get an odd number, so that the fan beam has a central ray. The number of foxels aw is proportional to the focal spot width. The peak image quality for a focal spot width of fw = 21 was reached with 18 foxels in Figure 17. Here we maintain this ratio: 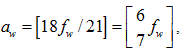 where the brackets indicate truncation to the nearest integer. For wide focal spots, foxels lead to substantially greater image quality than the point source approximation (consistent with[
where the brackets indicate truncation to the nearest integer. For wide focal spots, foxels lead to substantially greater image quality than the point source approximation (consistent with[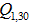 and
and 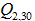 show that the quality is always higher when foxels are used (squares) than approximation of the focal spot as a point source (diamonds). However, these measures do not reflect visual image quality. Note that 0 on the abscissa corresponds to a point source.
show that the quality is always higher when foxels are used (squares) than approximation of the focal spot as a point source (diamonds). However, these measures do not reflect visual image quality. Note that 0 on the abscissa corresponds to a point source.