Take a look at the Recent articles

Abstract

Purpose: The purpose of this report is to develop analog electrical circuits, using resistors, capacitors, and constant current sources, which automatically calculate the stress and strain-rate response of viscoelastic biomaterials in response to arbitrary loading history, and to compare these with experimental strain-rate results from sclera subjected to constant and square-wave.

Methods: Electro-mechanical models of reversible and irreversible viscoelasticity are analyzed, using series and parallel combinations of springs and dashpots from the Kelvin-Voigt, Maxwell, and Jeffrey’s viscoelastic models. Experiments include strain-rate response of the sclera, applicable to the development of axial myopia.

Results: The resulting strain ε(t) versus time t is shown to vary exponentially for Kelvin-Voigt, as a linear step-ramp for Maxwell, and as a curved step-ramp for Jeffrey’s materials, consistent with experimental observations from cornea and sclera, corresponding to output voltage at the analog circuit capacitor V(t) in response to a step change in applied load σ(t) from 0 to σ o and a step change in applied current from 0 to Io at time t = 0. The cornea and sclera are rate-sensitive viscoelastic materials which stretch up to 12% in response to constant or repetitive loads. This is equivalent to an accumulated - 9.00 diopters of axial myopia.

Conclusions: The resulting analog equivalent circuits can be used as general purpose analog computers, to calculate system strain-rate ε(t), in response to arbitrary applied stress loading σ(t), including ramps, steps, sinusoids, and square waves, with variable intermittency factor. Results are applicable to collagen, cornea, sclera.                                       

Key words

viscoelasticity, cornea, sclera, axial myopia, analog electrical circuits, Maxwell material, Kelvin-Voigt model, stress, creep strain-rate

Introduction

Several authors report the creep-rate stress response of collagen with applications to myopia development, including Myers et al. [1], Phillips et al. [2], McBrien et al. [3], Siegwart & Norton [4], Ku & Greene [5], Nash et al. [6], Romano et al. [7], Genest et al. [8], Glass [9], Downs et al. [10]. Classical texts by Fung [11] and Ferry [12] provide basic equations and examples of the Maxwell and Kelvin-Voigt models. Humphreys [13] and Banks et al. [14] provide excellent reviews of the basic viscoelastic equations with applications to collagen.

In terms of similar cardio-vascular applications, Quick & Berger [15] present electrical analogues for the 2 and 3-element Windkessel model of the peripheral circulatory system, accounting for vascular resistance and compliance, using resistors and capacitors in series and parallel configurations. The applied input load for cardio-vascular applications is usually a variable intermittency square-wave pulse train, to simulate the heart as a mechanical pump.  The more complicated 4-element Windkessel model includes the inertial effects of the circulatory system, modeled with an inductor. These techniques are particularly useful in terms of calculating cardio-vascular pulse-wave reflections, modeling the circulatory system as a transmission line, using Smith-chart techniques [16-26].

Backhouse & Phillips [27], Liu et al. [28], and Lewis et al. [29] present experimental evidence of scleral creep causing myopia.

Clinical implications

Collagen material properties and tendency to distort permanently, are stability factors well-known to weaken with minor temperature increase, so during prolonged febrile disease, juveniles with glaucoma should be carefully monitored. In general, studies of the stress-strain and strain-rate response of cornea and sclera are applicable to glaucoma, keratoconus, and the development of progressive myopia.

Methods 

The various equivalent analog circuits, Figures 1-3, can be used as analog-computers in the laboratory, allowing almost immediate calculation of the resulting strain ε(t) as a function of time for different types of biomaterials, in response to complex applied stress loads σ(t) including step (Figure 4), ramp, sinusoidal, and square wave inputs (Figure 5).

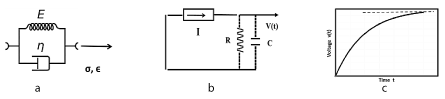
Figure 1. 1a: Kelvin-Voigt visco-elastic material, spring and dashpot in parallel; 1b: Constant current source I in series with an R-C parallel combination is equivalent in response to a Kelvin-Voigt material; 1c. Exponential voltage V(t) versus time  t  at the capacitor, for the Kelvin-Voigt model.

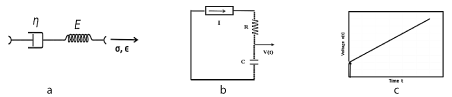
Figure 2. 2a: Maxwell visco-elastic material, spring and dashpot in series; 2b: Constant current source I in series with R-C, equivalent in to Maxwell material; 2c: Step-ramp voltage V(t) versus time at the capacitor.

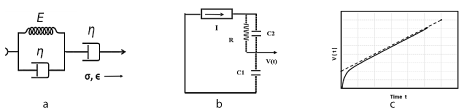
Figure 3. 3a: The Jeffreys visco-elastic material, Kelvin-Voigt in series with Maxwell model; 3b: Electrical circuit analog for Jeffreys material; Constant current source I  in series with R-C2 and C1; 3c: Curved step-ramp voltage V(t) versus time at the capacitor for Jeffreys.

All of these equivalent circuits, Figures 1-3, require a “constant current source”. The simplest possibility for a constant current source is a high-voltage supply, 120 volts AC, in series with a high resistance, 1,500 Ω, as shown in Figure 6. Over a range of intermediary load resistances, 50 Ω to 400 Ω, this circuit supplies an approximately constant current Io = V / R = 100 mA +/- 5%, as shown in Figure 6.

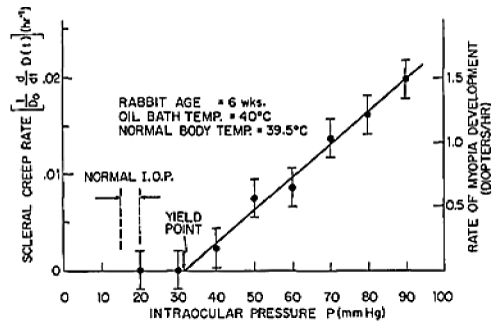
Figure 4. Irreversible scleral strain (creep) results from constant stress (I.O.P.) [6a].  Ocular shell material yields plastically at twice normal intra-ocular pressure.

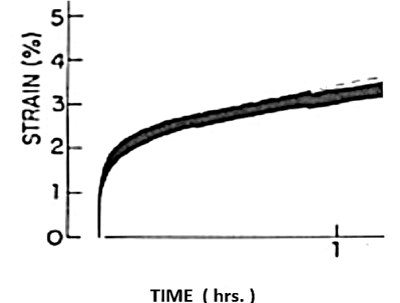
Figure 5. Viscoelastic creep-strain of the sclera under square wave pressure load displays Maxwell creep, accumulating 10% –12% strain after several hrs. (Ref. [6]).

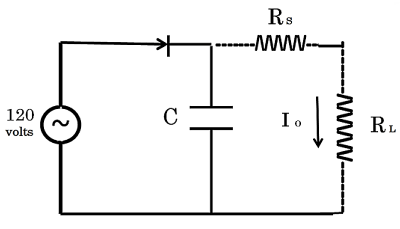
Figure 6      . Constant current source constructed from 120 v AC line voltage, with series resistor Rs = 1,500  Ω ,  storage capacitor C = 5,000 μF,   Io = 100 mA +/- 5%,  R_L = 50 Ω  to  400 Ω . 

More commonly, for models of this type, a “constant voltage source” is used, as a practical matter, realized with an ideal battery, in series with a low resistance, say, 1 Ω to 10 Ω.  Effectively, the only difference between a “constant current source” and a “constant voltage source”, is whether a large (1 kΩ ) or small (1 Ω) series resistor is used to power the intermediary load resistors, ( 50 Ω to 400 Ω ), thereby supplying either constant current or constant voltage.

For laboratory purposes, digitally controlled constant current sources are available commercially. For instance, B. K. Precision Co. makes several digitally controlled models, whereby a specified arbitrary current can be supplied, up to 5 amps. As a practical matter, there are always limits to the size of load that can be handled, based on the rated wattage of the device, typically 25W to 150W. The digitally specified 5 amps is supplied, regardless of the applied load resistance, which might have an acceptable range from 50 Ω to 400 Ω.

Laboratory experiments conform with ARVO guidelines for the use of animals in ophthalmic and visual research. The research was approved by the institutional review board (IRB). 

Results

Figures 1a, b, c shows the Kelvin-Voigt mechanical model, the equivalent electrical circuit, and resulting strain as a function of time, in response to a step load.

Figures 2a, b, c shows the Maxwell creep model, with spring and dashpot in series, corresponding to an equivalent

circuit, with resistor and capacitor in series.

Figures 3a, b, c shows the Jeffrey’s viscoelastic model, the simplest and most realistic model used to model cornea and sclera, with its equivalent electrical circuit.

Figure 4 presents experimental strain-rate data from rabbit sclera, in response to various constant loads (N=7), showing that plastic yielding occurs at twice normal intra-ocular pressure.

Figure 5, similar to Figure 4, presents rabbit sclera strain-rate in response to an applied square-wave stress load, exhibiting classical viscoelastic behavior.

Figure 6 is a schematic of a practical constant current source for laboratory purposes, powered by line voltage 120 v AC, using a single rectifier diode. The storage capacitor is used to minimize voltage fluctuations, which can be minimized further, with a larger capacitor and 4 element diode rectifier (not shown). This configuration produces 100 mA +/- 5% constant current, for reasonable load resistors RL.

Discussion

The plastic strain-rate of the sclera, in response to stress, as it applies to myopia development, is discussed by Myers et al. [1], Phillips et al. [2], McBrien et al. [3], Siegwart & Norton [4], Ku & Greene [5], Nash et al. [6], Romano et al. [7], and Downs et al. [8], Uchio et al. [16] using finite elements, calculate the stress fields caused by rapidly applied forces.

The three “constant current source models” developed here have several advantages, not the least of which is they are easily memorized. For instance, the series spring-dashpot system (the Maxwell creep model) results in an equivalent series R-C resistor-capacitor circuit, shown in Figure 2. Likewise, the familiar parallel spring-dashpot model of the Kelvin-Voigt viscoelastic material has an equivalent parallel R-C circuit, as shown in Figure 1. The Jeffreys viscoelastic-creep model, shown in Figure 3 and Figure 5, is the simplest way to predict cornea and sclera response to applied stress (Ku & Greene [5]; Nash et al. [6]). With all 3 models, the resulting strain as a function of time ε(t) is found as the equivalent voltage V_C(t) at the capacitor.

A spring-dashpot system is often used to model the human leg during running, using the Jeffrey’s model [17,18]. In addition, the material properties of the track surface, i.e. Tartan, polyurethane, Astroturf, Tuned Track, macadam, cinders, natural grass, plywood, fiberglass, etc., are modeled as a viscoelastic material [19-21].

These circuits are designed to respond to an input step change in applied current, from 0 to I₀  amps at t = t₀ , with this applied initial current step corresponding to a similar step in applied stress, from 0 to σ₀ [grams / mm^2 ] or [p.s.i.].  Then, the system output is given, in all 3 cases, by the voltage V(t) at the capacitor, corresponding to the strain rate function ε(t) [% per sec]. Using the super-position principle for linear systems, any combination of step, ramp, sinusoid, or square wave (with variable amplitude, frequency, and intermittency) the solution to the problem is immediately realized, using a multi-function signal generator.

Summary

Electrical circuit analogs of the viscoelastic stress-strain response of cornea and sclera are investigated, including the Kelvin-Voigt, Maxwell and Jeffrey’s, with particular attention to plastic yielding and creep.  The circuits are simple series and parallel combinations of resistors and capacitors, similar to the springs and dashpots of the respective mechanical models, powered by a constant current source. Resulting strain is measured as the voltage at the capacitor. Experiments are presented from rabbit sclera, including system response to constant and square-wave loading, showing that -9.00 diopters of axial myopia can be simulated in the laboratory in a few hours.

Conclusions

Using a constant current source for viscoelastic analog circuits, and the use of these circuits to simulate viscoelastic creep of cornea and sclera under constant and square-wave stresses, has not yet been reported in the literature as far as can be determined. By contrast, using a constant voltage source, it is somewhat easier to construct equivalent circuits. McEwen & Shepperd [22,23] use batteries, resistors and capacitor models to simulate tonometry of the human eye. To simulate the Heaviside load-step experiment, constant current source models are used as described here. The primary significance of the dashpot and capacitor velocity sensitive elements, is that rapidly applied forces (Uchio et al. [16]) can cause greater than normal stress levels, and that long-duration constant forces can result in irreversible accumulated plastic strain [5,6], equivalent to -9.00 diopters [24-26], typical of axial myopia.

References

1. Myers KM, Coudrillier B, Boyce BL, Nguyen TD (2010) The inflation response of the posterior bovine sclera. Acta Biomater 6: 4327-4335.  [Crossref]

2.       Phillips, JR, Khalaj M, McBrien NA (2000) Induced myopia associated with increased scleral creep in chick and tree shrew eyes. Invest Ophth Vis Sci 41: 2028-2034.  [Crossref]

3. McBrien NA, Jobling AI, Gentle A (2009) Biomechanics of the sclera in myopia: extracellular and cellular factors. Opt Vis Sci 86: E23-E30.  [Crossref]
4. Siegwart JT, Norton TT (1999) Regulation of the mechanical properties of tree shrew sclera by the visual environment. Vision Res 39: 387-407.  [Crossref]

5.       Ku DN, Greene PR (1981) Scleral creep in vitro resulting from cyclic pressure pulses: applications to myopia. Am J Optom Physiol Opt 58: 528-535. [Crossref]

6.       Nash IS, Greene PR, Foster CS (1982) Comparison of mechanical properties of keratoconus and normal corneas. Exp Eye Res 35: 413-424. [Crossref]

7. Romano MR, Romano V, Pandolfi A, Costagliola C, Angelillo M et al. (2017) On the use of uniaxial tests on the sclera to understand the difference between emmetropic and highly myopic eyes. Meccanica 52: 603-614. 
2021 Copyright OAT. All rights reserv
8. Genest R, Chandrashekar N, Irving EL (2013) Finite element model of the chick eye to study myopia. J Med Biol Engr 33: 215-220.

9.       Glass DH (2008) Characterization of the biomechanical properties of the in vivo human cornea.  Doctoral dissertation, Ohio State University.

10. Downs JC, Suh JK, Thomas KA, Bellezza AJ, Burgoyne CF, et al. (2003) Viscoelastic characterization of peripapillary sclera: material properties by quadrant in rabbit and monkey eyes.  J Biomech Eng 125: 124-131. [Crossref]
11. Fung YC (2013) “Biomechanics: mechanical properties of living tissues”, New York: Springer Science & Business Media.
12. Ferry JD (1980) “Viscoelastic properties of polymers”, New York: John Wiley & Sons.   
13. Humphrey JD (2003) Review Paper: Continuum biomechanics of soft biological tissues. Proc Roy Soc Lond A 459: 3-46.  
14. Banks HT, Hu S, Kenz ZR (2011) A brief review of elasticity and viscoelasticity for solids. Adv Appl Math Mech 3: 1-51.  
15. Quick CM, Berger DS, Noordergraaf A (1998) Apparent arterial compliance. Am J Physiol 274: H1393-H1403. [HTML][Crossref]
16. Uchio E, Ohno S, Kudoh J, Kisielewicz LT (1999) Simulation model of an eyeball based on finite element analysis on a supercomputer. Brit J Ophth 83:1106-1111. [Crossref]
17. McMahon TA, Greene PR (1979) The influence of track compliance on running.  J Biomech 12: 893-904. [Crossref]  

18.    Silva R, Tabouillot T (2012) Bio-electromechanical model of the muscle spindle.  IEEE Andean Region Int’l. Conf. (ANDESCON) VI: 143-146.

19. Roylance D (2001) “Engineering viscoelasticity”. Dept Materials Sci and Engr, Mass Inst Tech, Cambridge MA, 02139, 1-37.

20.    Gross B (1956) Electrical analogs for viscoelastic systems. J of Polymer Sci 20: 371-380. 

21. Ala G, Di Paola M, Francomano E, Li Y, Pinnola FP (2014) Electrical analogous in viscoelasticity. Commun Nonlinear Sci Numer Simul 19: 2513-2527.

22.    McEwen WK, Shepherd M, McBain EH (1967) An electrical model of the human eye. I. The basic model. Invest Ophth Vis Sci 6: 155-159.  [Crossref]

23.    Shepherd M, McBain EH, McEwen WK (1967) An electrical model of the human eye. II. The model and the eye during tonography. Invest Ophth Vis Sci 6:160-170. [Crossref]

24. Greene PR (1987) Stress amplification and plastic flow for spheroidal shells: Applications to myopia. Rheologica Acta 26: 479-484.

25.    Greene PR, Brown OS (2017) Review.  +2 D. to +3 D. Reading Glasses to Prevent Myopia.  EC Ophthalmol 5: 11-27. 

26. Greene PR, Medina A (2016) Analogue computer model of progressive myopia–refraction stability response to reading glasses.  J Comput Sci Syst Biol 9: 104.

27.    Backhouse S, Phillips JR (2010) Effect of induced myopia on scleral myofibroblasts and in vivo ocular biomechanical compliance in the guinea pig.  Invest Ophthalmol Vis Sci 51: 6162-6171. [Crossref]

27. 28.    Liu S, Li S, Wang B, Lin X, Wu Y, et al. (2016) Scleral Cross-Linking Using Riboflavin UVA Irradiation for the Prevention of MyopiaProgression in a Guinea Pig Model: Blocked Axial Extension and Altered Scleral Microstructure. PLoS One 11: e0165792. [Crossref]
28. 29.    Lewis JA, Garcia MB, Rani L, Wildsoet CF (2014) Intact globe inflation testing of changes in scleral mechanics in myopia and recovery.   Exp Eye Res 127: 42-48. [Crossref]