We present an extension to 29 parcels of our earlier 5 parcel cerebellar segmentation method based on active shape and appearance modeling. The 29 parcel segmentation was trained on expert hand delineated parcellations of prospective motion corrected 0.7 mm3 images. Test-retest reliability and an expert agreement validity assessment is presented, and the method is then applied to images from adolescents with histories of prenatal alcohol exposure (PAE) and non-exposed controls (NC) that had been previously analyzed with the 5 parcel method. The additional insights from the 29 parcel segmentation regarding the effects of PAE on the cerebellum are then presented.
cerebellum, active appearance models, segmentation, prenatal alcohol, MRI
The cerebellum is a key region for integration of information for both motor and non-motor functions, and cerebellar abnormalities may underlie some of the sensory-motor, cognitive, and emotional deficits observed in many disorders, including alcoholism and other addictions.
Cerebellar structure and connectivity
The cerebellum receives extensive afferent input from prefrontal and association cortices relayed via pontine nuclei. Rs-fMRI demonstrates cerebellar involvement in neocortical functional networks, and cerebellar activation with a variety of cognitive and affective brain functions, including those related to addiction (i.e., insight, reward, motivational drive, saliency, and inhibitory control). The cerebellum has an outer cortical gray matter layer, with an inner layer of white matter scaffolding. Input is received through two major brainstem afferent relays (shown in Figure 1), the inferior olive and the pontine nuclei, via climbing fiber (through the inferior cerebellar peduncle) and mossy fiber (through the inferior cerebellar peduncle) pathways. Both pathways relay cortical inputs (including from non-motor cortical regions) to the cerebellum (reviewed in Schmahmann [1,2]. Given its highly uniform neuronal structure, the cerebellum has been hypothesized to have a single generalizable function [3-5]) – modulating and optimizing activation in different domains depending on the cerebral inputs the cerebellar region receives. This theory suggests that the cerebellum acts as an oscillation dampener, optimizing performance by modulating behavior
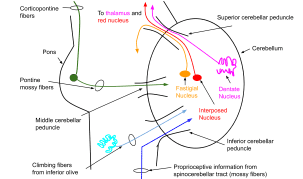
Figure 1. Schematic of the cerebellar circuitry
and affect according to context. For example, the cerebellum may modulate emotional processes by integrating positive and negative affective inputs in the same way that it modulates fine motor control by integrating sensory inputs.
A feedforward loop of the cerebrocerebellar circuit is comprised of projections from the prefrontal cortex to the pons, followed by projections from the pons to the cerebellum (i.e., the corticopontocerebellar system). The feedback loop of this circuit is comprised of cerebellum projections to the premotor and prefrontal cortices via the thalamus (i.e., the cerebellothalamocortical system). Volume shrinkage of any nodes within these cerebrocerebellar circuits, or white matter damage to any of the connecting fibers, may underlie cognitive, affective, and motor deficits of functions that require cerebellar involvement for optimum performance.
Cognitive function and the cerebellum
Many cognitive tasks that require prefrontal cortex also involve the cerebellum. Diamond [6] reviewed the literature showing the close interrelationship of motor, cognitive, and affective development and also the lockstep development of the neocerebellum and dorsolateral and dorsomedial prefrontal cortex. (i.e., most cognitive and emotional tasks involving dorsolateral or dorsomedial prefrontal cortex also involve the neocerebellum). fMRI studies show that the cerebellum and prefrontal cortex co-participate when tasks are: a) difficult, b) novel vs. familiar and practiced, c) unstable, d) require speed, and e) in general, are unable to operate on automatic pilot. Lesions in prefrontal cortex are often associated with contralateral cerebellar hypometabolism and neocerebellar lesions can be associated with frontal hypometabolism. The protracted duration of prefrontal maturation is well appreciated, while the similarly protracted period of neocerebellar maturation is relatively ignored or only newly appreciated. This is true despite numerous studies showing close coactivation of the neocerebellum with dorsolateral or dorsomedial prefrontal cortex during cognitive tasks. When prefrontal activation is increased or decreased, corresponding increases or decreases in activation of contralateral cerebellar cortex are observed. Using rudimentary measurements of cerebellar, pontine, thalamic, and cortical volumes, it has been shown that disruption of the corticopontocerebellar and cerebellothalamocortical systems is related to cognitive deficits in alcoholism (i.e., see [7]). This short review suggests that a full understanding of role of the prefrontal cortex in the development of alcoholism and other addictions could only be fully appreciated if cerebellar involvement is studied in the same cohorts as the cerebrum.
The cerebellum's role, as a modulator, fits in nicely with existing models of addiction. The iRISA (Impaired Response Inhibition and Salience Attribution) four-circuit model of addiction [8-10] provides a framework for the cerebellum’s possible role. The iRISA model consists of inter-connected circuits for memory, reward/saliency, executive control, and motivation/drive. Behavior in response to potential rewards is mediated by interactions among these four circuits. In the actively addicted brain, the appetitive drive components of these circuits are amplified, while the inhibitory control and emotion regulation components are diminished (see our studies reviewed in [11]). A model for the cerebellum’s role in addiction is that it is influential in maintaining the homeostatic balance of the iRISA circuits. [12].
Neuroimaging research in addiction [7,13-18] implicates cerebellar gray matter deficits in Lobule VI, VIIb, Crus I, Crus II, and the vermis in the cerebellum's impaired ability to integrate activity across the iRISA component functions. In an analysis of functional connectivity in a large dataset of about one thousand healthy subjects, cerebellar regions were associated with multiple cerebral resting state networks. Lobules VI, VIIb, and Crus I were associated with dorsolateral and dorsomedial prefrontal cortex networks related to cognitive control [19], in agreement with other studies in smaller samples [12,20,21], and with tracer studies in non-human primates showing connections between these cerebellar and cerebral areas (see [22]). In the addicted brain, impaired modulation (inhibition) of brain circuits related to reward/salience, motivational drive, and memory results in an increased drive toward externalizing behavior, while disruption of reciprocal pathways related to executive control and emotion regulation interferes with inhibition of unwanted drug seeking behavior. Finally, a number of studies suggest that abnormal cerebellar structure may partially characterize the genetic risk for alcoholism [23-27]. Although the cerebellum has been acknowledged as being impaired by addiction, its role in the maintenance of addiction has received relatively little attention. Moreover, no developmental studies of the CNS predispositions and consequences of addiction in adolescents have included a focus on the cerebellum.
Critical barriers to studying the cerebellum
Despite the accumulating evidence that cerebellar damage is likely important in alcohol and other substance use disorders, very few human neuroimaging studies have included a focus on the cerebellum, in part due to the paucity and limitations of automated cerebellar segmentation algorithms. The cerebellar anatomy has foliations narrower than the resolution of standard 1 mm isovoxel T1-weighted MR Images, indistinct lateral vermis boundaries, and close proximity to the base of the skull (with its attendant image contrast nonuniformities), all of which pose challenges for automated segmentation algorithms. As a result, many initial human cerebellar imaging studies in addiction used manual tracings to measure cerebellar volumes [18,26,28]. With the wide availability of MRIs and the development of relatively fast MRI structural imaging sequences, the need for high output tools for cerebellar measurement has become acute. Owing to the growing awareness of the importance of the cerebellum in development and disease, there has been a recent drive to solve the challenge of segmenting the cerebellum into its constituent components [29,30]. Our laboratory has spent the last five years developing software for automated, reliable, and valid delineation of the complex morphometry of the cerebellum. Initially, using Bayesian Active Appearance Modelling (AAM) [31] we developed a five-parcel cerebellar segmentation with outstanding reliability and validity [32]. We also applied the 5-parcel delineation to Prenatal Alcohol Exposed (PAE) and control children, demonstrating cerebellar findings in PAE that existed beyond the frequently observed general pattern of microcephaly [33]. We recently extended this AAM approach to 29-parcel cerebellar segmentation. Below, we describe the 29-parcel segmentation implementation, present its reliability and validity and apply it to the PAE data above [33], showing where in the cerebellar hemispheres and vermis the PAE effects are the largest.
Segmentation of MR brain images into anatomical regions is one of the most difficult tasks in image processing. Many techniques exist
to divide a medical image into regions with similar properties such as gray level, color, texture, brightness and contrast, or to partition an image based on abrupt changes in intensity, such as edges.
Background
Early techniques based on gray level features such as histogram thresholding, edge based segmentation, and region based segmentation generally did not perform well on brain images with complex anatomy [34]. As noted above, segmentation of the cerebellum is especially challenging, because the cerebellar foliations are narrower than 0.5 mm. This results in extensive partial volume effects at the standard 1 mm3 resolution of T1-weighted images. Therefore, any segmentation method that seeks to delineate more than the outer cerebellar boundary must be able to leverage strong prior assumptions about local shape and image intensity, as well as relative dependencies or landmarks that human experts use to infer object boundaries in medical images. The most popular methods for medical image segmentation are atlas based approaches that seek to deform known template images with associated labels (atlas) so as to match with novel subject images thereby allowing a label mapping to be established. An example of this is FreeSurfer [35], which is widely used and among other workflows, uses nonlinear template registration to align subject images to a stereotaxic atlas. Atlas based segmentation relies on appropriate atlas formation and selection, and accurate registration (alignment) of the atlas to the image to be segmented. Early brain atlases were based on a single individual, such as the Talairach atlas [36], and failed to adequately reflect anatomic variability. Other atlases derived from averaging multiple brain images after affine normalization (i.e., correcting for translation, rotation, scale, and shear), resulted in blurry templates [37,38]. The utility of such atlases for defining anatomic structures and propagating them to individual images (i.e. atlas-based segmentation) was limited, as the spatial uncertainty of blurry atlases caused co-registration problems, even with high-parameter volume registration methods, that degraded label propagation accuracy. Aligning an image with an atlas typically comprises deforming the atlas template volume so as to minimize differences between the template and the new image. Initial deformation normally uses a linear transformation to account for gross rigid differences (i.e. a similarity or affine transformation), after which a non-linear deformation introduces more flexibility in order to account for the remaining differences. A difficulty with the latter process is balancing the number of degrees of freedom of the parameterization for deformation with regularization and smoothness constraints. A number of methods [39-42] have been proposed towards providing reliable non-rigid deformation for achieving accurate template alignment. However, while methods continue to improve for the cortical regions, to-date none of these approaches have been able to reliably align detailed structures such as cerebellar lobules. Some work [43] has shown improved results when combining registered output with machine learning techniques, such as training a Support Vector Machine to classify the final output labels instead of using the maximum atlas probability map directly. More recently, there has also been significant growth in application of Convolutional Neural Networks to brain imaging, such as tissue classification, identification of tumors, and even tackling semantic segmentation [44-46]. However, again while this is an active area of research, reliable detailed delineation for intricate structures like cerebellar foliations has not yet been achieved.
An alternative to deforming the entire volume of a template for obtaining alignment is to only deform surface boundaries (another prevalent category of 3D segmentation methods), which encompasses deformable models such as active contours and surfaces [47,48]. Restricting deformation to a surface manifold instead of a volume has the benefit of a lower parametrization complexity and allows intuitive features such as shape to be modeled explicitly. This comes at the expense of losing the ability to map voxels within a boundary between template and subject, i.e. it is only possible to determine whether a particular voxel falls inside or outside the boundary, but there is no precise correspondence of that voxel between aligned images since no internal deformation warp has been defined. In the context of segmentation for the purpose of localizing a region and measuring volume, this limitation is irrelevant. In fact, for volumetric measurement surface based methods offer a direct approach, and greater resilience against quantization error since sub-voxel estimates can be made by exact integration of the polyhedral surface.
Active appearance models
Extending the aforementioned advantages of surface based segmentation, Active Shape Models (ASM) [49,50] and Active Appearance Models (AAM)[49-51] provide a framework for learning statistical surface shape and intensity models from labeled data and adapting these models to new images. This approach is therefore well-aligned to the requirements of cerebellar segmentation, which is highly sensitive to shape and local intensity distributions. We adopted the Bayesian Active Appearance Modeling (AAM) formulation [31] in our implementation of our 5-parcel Cerebellar Analysis Tool Kit (CATK) [32]. The AAM is trained from hand-labeled T1-weighted examples (Neuromorphometrics, Inc.) derived from healthy participants, and uses a Point Distribution Model (PDM) [49-50] to represent shape and intensity variation at the volume’s borders. The model is constructed by co-registering [52,53] the hand-labeled surfaces, and generating mesh models with vertex correspondence across the set of training subjects. Eigen decomposition under the assumption of a multivariate Student Distribution produces a linear subspace that describes the characteristic modes of shape variation. Similarly, a similar process can be applied to sampled intensity profiles taken normal to each surface vertex to produce a linear subspace describing the characteristic modes of intensity variation. Linear combinations of the mode vectors allow the model to interpolate the gamut of variation seen in the training data while also enforcing probabilistic priors.
An obvious concern is that the AAM model can suffer from inflexibility and fail to provide adequate freedom to account for unseen variation (which is more appropriately handled by some non-rigid voxel methods); however, within the cerebellum we have observed limited variability from the average shape, especially with respect to localized sub-regions. Furthermore, we maintain that the AAM offers a better trade-off between flexibility and parameter smoothness because the parameterization is not arbitrary, but rather is tailored specifically (through statistical modeling) to the cerebellar structure. Another advantage of the AAM approach is that the inter-relationship between shape and intensity is modeled and used to drive the fitting process, while atlas-based approaches are limited to intensity similarity and assumed parameter smoothness. More specifically: although the atlas itself offers structural priors, this information is not generally used to guide fitting. We have found that this difference causes AAM fitting to be more robust since worst-case errors still maintain likely parameterization, while atlas-based methods can fail spectacularly, if the initial conditions are suboptimal.
Extending CATK to 29 cerebellar parcels
Our original implementation of CATK demonstrated reliable and valid delineation on 5 cerebellar parcels: two cerebellar hemispheres and three vermal lobes (anterior: vermis lobules I-V, superior-posterior: vermis lobules VI-VII, and inferior-posterior: vermis lobules VIII-X). Validity of the method was attained by comparing volume and dice overlap measures (from non-training images) to the expert manual delineations provided by Neuromorphometrics (NMI); the gold standard for structural image analysis tools. Comparison with SUIT toolbox for SPM [29] (an atlas-based method) showed that CATK offers superior test-retest reliability (ICCs of 0.95 versus 0.62) on repeat scans from 20 subjects and better agreement with expert hand delineations [32].
Subsequently, we have extended this approach to 29 cerebellar parcels (CATK2). While the underlying labeling protocol is actually based on 32 parcels (Figure 2), a reduction to 29 parcels was ultimately adopted due to some very small structures being found to be unreliable from both the manual and automatic labeling perspectives. Specifically, in the vermis we merge Crus I, Crus II, VIIb (referred to as VIIcab), and VIIIa and VIIIb (referred to as VIIIab). In order to address the physical barriers of delineating submillimeter cerebellar foliations, new high resolution 0.7 mm3 training data was acquired using prospective motion tracking and correction. This enabled us to acquire high-quality T1-weighted images from both controls and alcoholics suitable for manual labeling (and ultimately machine learning) that would otherwise have been heavily degraded due to micro-movements of subjects in the scanner and higher partial volume effects due to the longer scan time required for higher resolution images.
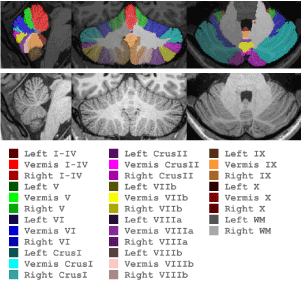
Figure 2. CATK2 Parcellation Map
A total of 63 high-resolution motion-corrected images from 38 subjects (alcoholics and controls, men and woman) were collected for modeling, with 25 subjects having same-day repeat sessions that are used to assess reliability of both manual and automated methods. Expert manual labeling, based on the parcellation scheme shown in Figure 2, were generated for these subjects by NMI using advanced interactive landmarking tools that they specifically developed for this detailed cerebellar delineation.
The processing pipeline for CATK2 (shown in Figure 3) is more extensive than the original 5-parcel system, and employs a hierarchical modeling approach that applies a coarse-to-fine methodology. Multiple AAM’s have been constructed that target the: whole cerebellum, white matter portions, hemisphere lobules, and vermal lobules, with vertex density progressively increasing at each level. Processing is divided into 3 stages: (1) image registration and initial alignment, (2) application of a hierarchical array of appearance models, and (3) post-processing for refining the output labels. The pipeline also incorporates the ability to use multiple templates for registration which enables multiple starting points for fitting.
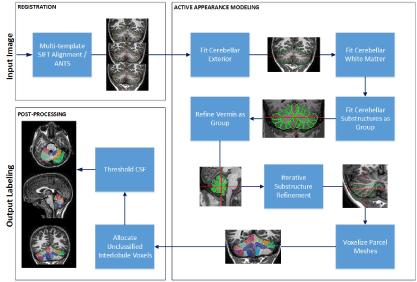
Figure 3. CATK2 Processing Pipeline
Registration and alignment
Initial registration is necessary (for both training and fitting) to remove common rigid variation (translation, scale and orientation) between subjects that does not contribute to inter-subject shape differences. For 0.7mm3 motion-corrected images, which have improved detail, CATK2 uses multiple templates with 3D-SIFT (an extension to the 2D Scale Invariant Feature Transform) [42] as the registration engine, while linear registration with ANTS (Advanced Normalization Tools) [54] is used for conventional 1mm3 images. When using the multi-template approach, T1 images from the AAM training set are used as templates (where the median alignment taken), whereas the MNI-152 0.5mm3 T1 template is used in the single-template. Both cases use a 9 parameter (rotation, translation and scale for each axis) rigid linear transform.
Given two images to be registered, 3D-SIFT proceeds by applying feature extraction to each image, which identifies distinct interest points and generates normalized descriptors for each point. Nearest-neighbor matching is used to identify candidate correspondences across the images, and RANSAC (Random Sample Consensus) is applied in order to determine the largest subset of matches that is consistent with a similarity transform. Rotational invariance is provided through the structure tensor.
Active Appearance models
Active Shape Models (ASM) [49,50] and Active Appearance Models (AAM) [50] encapsulate variation from real examples and restrict the search space to linear combinations of these examples. The key distinction between the two is that AAMs also explicitly models image intensity (in addition to shape) and allow adaptation to take advantage of the interrelationships between shape and intensity. The capture region refers to a zone which encompasses the set of solutions that converge to the target object. As such models that are initialized close to the capture region generally have a high convergence rate; hence large capture regions are desirable. CATK2 uses both ASM and AAM under a Bayesian formulation [31]: the former provides a larger capture region, which allows the initial starting point to converge more reliably, while the latter offers better estimation in the presence of noise due to its joint prior.
Models are generated by extracting 3D surfaces from the manual label volumes (where each voxel is associated with a specific cerebellar parcel) and applying the training procedure. Each surface is parameterized by a triangular mesh that this generated using Marching Tetrahedra (MT) [55] to extract the iso-surface from the underlying volume. Iterative decimation is used to simplify each mesh while ensuring that the residual error does not stray below 1 voxel. Next an average mesh is generated by aligning the input meshes to a common space, filling the volume and extracting a mesh surface using the same procedure as before. We use fast marching [56] to uniformly resample the average mesh to several resolutions as appropriate for our modeling hierarchy (typically 200 vertices for most small parcels, and 500 to 1000 vertices for larger parcels like the hemispheres or cerebellar exterior). The average meshes are then iteratively deformed to match each original subject mesh resulting in a set of meshes for each parcel and resolution that achieve point correspondence between the training subjects. Figure 4 shows the output of this procedure that produces multi-resolution corresponding surface models using various label grouping schemes.

Figure 4. Average CATK2 models for 4 parcel groupings and 2 mesh resolutions: 100 vertices (top) and 800 vertices per surface (bottom)
Once correspondences are established, statistical shape (and intensity) models are computed by treating each mesh as a column vector and concatenating subjects into a data matrix. For intensity models, linear profiles normal to the surface at each vertex are sampled (details described in [32,57]). Eigen decomposition of the data matrix yields a low-dimensional parameter space that represents the most common modes of variation. Parcels can be jointly modeled in this way or modeled relative to one-another in order to boost modeling precision for a specific area; CATK2 uses a full joint model followed by a series of individual conditional model refinements.
Model fitting
CATK2 uses a 3-stage fitting process: First, an ASM with zero maximum standard deviation is applied. This amounts to disabling shape adaptation but allowing 3D translation and overall scale to be adjusted, and acts as a pre-tuning step to account for minor offsets introduced by registration. Second, the ASM limits are removed and the model is allowed to adapt: ASM fitting comprises searching for intensity profile matches normal to the surface using 1D gradient correlation and selecting the shape mode parameters whose surface is closest to these matches. In this way we can adapt the model vertices towards proposed candidate locations where the intensity profile is consistent with the model, but retain smoothness by selecting the closest shape in the modeled subspace. Finally, we activate the full AAM that is driven by an optimization process (L-BFGS: Limited Memory Broyden-Fletcher-Goldfarb-Shanno) where the shape parameters are adjusted and the objective error function is the posterior likelihood function of the conditional distribution between intensity on shape.
For hierarchical fitting, successive stages are initialized by optimizing the shape parameters for the next stage using the conditional distribution between the prior and latter shape models. For example, when moving from cerebellar exterior fitting stage to lobule fitting stage, we maximize the likelihood of lobule shape parameters conditioned on the current exterior shape and intensity from the first stage.
Post-processing
After model fitting, a fitted 3D surface is defined for each output label region, and is converted to an output label map by voxelizing (filling) each fitted mesh and applying its contributing label. Owing to quantization errors introduced by the close proximity of lobule meshes and the voxelization process, some voxels between lobules can be excluded for label generation. Therefore, we use the fitted exterior cerebellar model as a bounding surface to locate missed voxels that fall between the interior lobule mesh surfaces. Finally, we classify interior voxels as being part of the cerebellum or CSF by thresholding the intensity. The threshold is determined using a ratiometric analysis of the intensity range over the image and the distribution of intensities falling inside the parcel. CSF voxels are suppressed and unlabeled non-CSF voxels are allocated to their closest parcel.
Below we present some reliability validity results for the method and a beginning application of the method to children with prenatal alcohol exposure from control children.
Validation and reliability
CATK2 was developed using images from 38 adult subjects from a larger study on the long-term effects of alcohol. Twenty-five subjects had same day repeat scans (with the subject exiting the scanner between scans), and the agreement between these scans was used to estimate the reliability of both manual labeling and our automated method. The reliability estimates thus includes partial volume effects (resulting from sub-voxel variability in subject positioning and variability in tissue vs. voxel boundaries). Each study consisted of two 0.7 mm3 T1 motion-corrected studies, one 1 mm3 T1 motion-corrected study, and one 1 mm3 T1 non-motion corrected study. Table 1 shows intraclass correlations (ICC) and dice overlap scores between CATK2 and the manual labelings for major cerebellar groupings. Owing to the small number of labeled subjects and the requirements on sufficient data to generate a viable AAM, only leave-one-out evaluation was feasible.
Table 1. Comparison of CATK2 and Manual labelings for major cerebellar lobes
GROUPING |
INTRACLASS CORRELATION |
|
DICE |
| |
Test-Retest Reliability |
|
Validity |
|
Dice Overlap |
| |
Manual |
CATK2 |
|
Manual vs. CATK2 |
|
Manual vs CATK2 |
Whole Cerebellum |
0.9577 |
0.9772 |
|
0.8957 |
|
0.93 |
Left Hemisphere |
0.9454 |
0.9696 |
|
0.8723 |
|
0.89 |
Right Hemisphere |
0.9475 |
0.9724 |
|
0.8759 |
|
0.89 |
Vermis |
0.9140 |
0.9768 |
|
0.7976 |
|
0.83 |
Corpus Medullare |
0.7386 |
0.8687 |
|
0.5052 |
|
0.85 |
Anterior Lobe (I-V) |
0.9347 |
0.8014 |
|
0.5273 |
|
0.78 |
Superior Posterior Lobe (VI-VII) |
0.8449 |
0.9636 |
|
0.7775 |
|
0.89 |
Inferior Posterior Lobe (VIII-IX) |
0.6817 |
0.948 |
|
0.6473 |
|
0.85 |
Flocculonodular Lobe (X) |
0.6398 |
0.8564 |
|
0.4071 |
|
0.60 |
Vermis I-V |
0.8662 |
0.9645 |
|
0.7721 |
|
0.80 |
Vermis VI-VII |
0.8208 |
0.9497 |
|
0.693 |
|
0.77 |
Vermis VIII-X |
0.9454 |
0.9154 |
|
0.6544 |
|
0.79 |
Test-retest scores refer to ICC’s computed between repeat scans for each method (Manual or CATK2), while validity scores are computed comparing manual labelling to CATK2 results. Dice Overlap [58] measures the spatial overlap between two discrete segmentations by measuring the proportion of voxels that have the same label as a percentage of the total masked volume. (All validity comparisons are based on the set of 0.7mm3 motion corrected images which were selected for manual labeling.)
A similar comparison of reliability and validity for all 29 cerebellar parcels is shown in Table 2. Generally, CATK2 shows excellent repeatability when applied to multiple scans of the same subject as seen in the high test-retest scores, which are similar, and typically higher, than the scores for manual labeling. Dice overlap, which is calculated as the mean across both test and re-test scans, also indicates fairly consistent agreement with manual labelings. However, lower scores are seen in cases of smaller parcels, and especially where poor agreement is seen in the manual labels between test and re-test scans.
Table 2. Comparison of CATK2 and Manual labelings for each parcel
|
PARCEL |
INTRACLASS CORRELATION |
|
DICE |
| |
|
Test-Retest Reliability |
|
Validity |
|
Dice Overlap |
| |
|
Manual |
CATK2 |
|
Manual with CATK2 |
|
Manual vs CATK2 |
1 |
Left I-IV |
0.7134 |
0.8892 |
|
0.3083 |
|
0.62 |
2 |
Right I-IV |
0.7601 |
0.7816 |
|
0.2773 |
|
0.68 |
3 |
Left V |
0.5810 |
0.5209 |
|
0.2102 |
|
0.62 |
4 |
Right V |
0.7886 |
0.6810 |
|
0.2509 |
|
0.65 |
5 |
Left VI |
0.8497 |
0.8491 |
|
0.4206 |
|
0.78 |
6 |
Right VI |
0.9558 |
0.9038 |
|
0.5905 |
|
0.78 |
7 |
Left CrusI |
0.5812 |
0.9447 |
|
0.5348 |
|
0.82 |
8 |
Right CrusI |
0.9423 |
0.9207 |
|
0.7812 |
|
0.82 |
9 |
Left CrusII |
0.2432 |
0.7836 |
|
0.3892 |
|
0.77 |
10 |
Right CrusII |
0.4416 |
0.9156 |
|
0.4125 |
|
0.77 |
11 |
Left VIIb |
0.5614 |
0.5923 |
|
0.2850 |
|
0.57 |
12 |
Right VIIb |
0.8506 |
0.8678 |
|
0.5160 |
|
0.65 |
13 |
Left VIIIa |
0.4923 |
0.7749 |
|
0.3195 |
|
0.60 |
14 |
Right VIIIa |
0.6903 |
0.9706 |
|
0.4845 |
|
0.70 |
15 |
Left VIIIb |
0.3068 |
0.6582 |
|
0.2458 |
|
0.69 |
16 |
Right VIIIb |
0.2938 |
0.9301 |
|
0.3756 |
|
0.74 |
17 |
Left IX |
0.9801 |
0.9209 |
|
0.7653 |
|
0.78 |
18 |
Right IX |
0.9663 |
0.8693 |
|
0.6392 |
|
0.79 |
19 |
Left X |
0.6585 |
0.8299 |
|
0.3829 |
|
0.57 |
20 |
Right X |
0.5268 |
0.8097 |
|
0.4132 |
|
0.59 |
21 |
Vermis I-IV |
0.8300 |
0.8757 |
|
0.6838 |
|
0.81 |
22 |
Vermis V |
0.7208 |
0.6856 |
|
0.5205 |
|
0.72 |
23 |
Vermis VI |
0.7271 |
0.9128 |
|
0.7295 |
|
0.73 |
24 |
Vermis VIIcab |
0.6394 |
0.8187 |
|
0.4759 |
|
0.69 |
25 |
Vermis VIIIab |
0.8921 |
0.8786 |
|
0.5844 |
|
0.77 |
26 |
Vermis IX |
0.8334 |
0.8018 |
|
0.5933 |
|
0.76 |
27 |
Vermis X |
0.7612 |
0.8882 |
|
0.5585 |
|
0.66 |
28 |
Right Corpus Medullare |
0.7252 |
0.8660 |
|
0.5000 |
|
0.86 |
29 |
Left Corpus Medullare |
0.7471 |
0.8626 |
|
0.5029 |
|
0.85 |
We also applied CATK2 to 37 unseen control and alcoholic subjects from the study (not used for training or validation) to assess reliability of the method on multiple image resolutions. Table 3 shows ICC scores computed between each subject’s initial and follow-up scan for 0.7mm3 motion-corrected, 1mm3 motion-corrected, and 1mm3 standard studies respectively. The first column shows the overall agreement across all image resolutions. This comparison shows that even though CATK2 was trained on high-resolution motion-corrected image, the models can be applied to standard resolution non motion-corrected image with no noticeable impact on reliability.
Table 3. CATK2 reliability for first and follow up visits applied to different image resolutions
|
PARCEL |
INTRACLASS CORRELATION CATK2 Visit1 vs Visit2 |
| |
|
|
| |
|
ALL |
0.7mm3 MOCO |
1mm3 MOCO |
1mm3 |
1 |
Left I-IV |
0.9277 |
0.9069 |
0.9617 |
0.9708 |
2 |
Right I-IV |
0.9544 |
0.9619 |
0.9716 |
0.9743 |
3 |
Left V |
0.9480 |
0.9368 |
0.9740 |
0.9707 |
4 |
Right V |
0.9375 |
0.9171 |
0.9721 |
0.9426 |
5 |
Left VI |
0.9453 |
0.9223 |
0.9560 |
0.9587 |
6 |
Right VI |
0.9575 |
0.9295 |
0.9599 |
0.9657 |
7 |
Left CrusI |
0.9549 |
0.9392 |
0.9637 |
0.9776 |
8 |
Right CrusI |
0.9624 |
0.9394 |
0.9692 |
0.9737 |
9 |
Left CrusII |
0.9505 |
0.9368 |
0.9760 |
0.9530 |
10 |
Right CrusII |
0.9587 |
0.9655 |
0.9697 |
0.9541 |
11 |
Left VIIb |
0.9122 |
0.8688 |
0.9411 |
0.9132 |
12 |
Right VIIb |
0.9345 |
0.9347 |
0.9423 |
0.9448 |
13 |
Left VIIIa |
0.9260 |
0.8865 |
0.9295 |
0.9390 |
14 |
Right VIIIa |
0.9639 |
0.9463 |
0.9695 |
0.9692 |
15 |
Left VIIIb |
0.9002 |
0.8395 |
0.8824 |
0.9228 |
16 |
Right VIIIb |
0.9483 |
0.9085 |
0.9558 |
0.9755 |
17 |
Left IX |
0.9607 |
0.9523 |
0.9783 |
0.9689 |
18 |
Right IX |
0.9662 |
0.9621 |
0.9775 |
0.9734 |
19 |
Left X |
0.9111 |
0.8818 |
0.9190 |
0.9056 |
20 |
Right X |
0.9227 |
0.9317 |
0.9503 |
0.9367 |
21 |
Vermis I-IV |
0.9470 |
0.9656 |
0.9683 |
0.9785 |
22 |
Vermis V |
0.9166 |
0.9431 |
0.9526 |
0.9604 |
23 |
Vermis VI |
0.9642 |
0.9470 |
0.9802 |
0.9745 |
24 |
Vermis VIIcab |
0.9053 |
0.8637 |
0.9197 |
0.9423 |
25 |
Vermis VIIIab |
0.9439 |
0.9544 |
0.9708 |
0.9604 |
26 |
Vermis IX |
0.9339 |
0.9455 |
0.9525 |
0.9510 |
27 |
Vermis X |
0.9012 |
0.9283 |
0.9423 |
0.9520 |
28 |
Right Corpus Medullare |
0.9572 |
0.9480 |
0.9578 |
0.9640 |
29 |
Left Corpus Medullare |
0.9581 |
0.9524 |
0.9602 |
0.9663 |
Application of CATK2 to prenatally alcohol exposed and control children
We previously applied the 5-parcel CATK to samples of prenatal alcohol exposed and control children [33], which revealed new findings relative to the effects of prenatal alcohol exposure on the brain. Subsequently, we have now applied CATK2 to the same data, which comprises two groups of children between 10 and 18 years of age: 13 children with histories of heavy prenatal alcohol exposure (PAE group) and 9 non-exposed control children (NC group). Children were part of a larger study of the behavioral teratogenicity of alcohol. Inclusion required having English as the primary language, no history of head trauma, serious medical condition, or MRI contraindications.
Inclusion in the PAE group required documented heavy maternal alcohol consumption during pregnancy, defined as 4 or more alcoholic drinks per single occasion at least once per week, or 14 or more drinks per week on average. Whenever possible, exposure was confirmed using medical history, birth records, social services records, or maternal report. However, direct maternal report was not common as many of these children no longer resided with their biological families. Thus, precise details about alcohol consumption (i.e., dose and timing) were often unavailable. In these cases, mothers were reported to be alcoholic or alcohol abusing or dependent in pregnancy. In addition to psychometric testing and questionnaire screening, a diagnosis of FAS was determined by Dr. Kenneth Lyons Jones, a dysmorphologist, using a standardized assessment [59,60]. FAS was diagnosed in the presence of structural abnormality (i.e., two or more of the following facial features: short palpebral fissure length, smooth philtrum, thin vermillion border) and either growth deficiency (height or weight is < 10th normative percentile) or microcephaly (occipital–frontal circumference is < 10th normative percentile).
Based on this screening process, 6 alcohol-exposed children received a diagnosis of FAS.
Children in the NC group were excluded if greater than minimal prenatal alcohol exposure was reported. Figure 5 shows coronal and sagittal sections from two PAE and two control subjects, with CATK2 parcel labels, illustrating the qualitatively good fits.
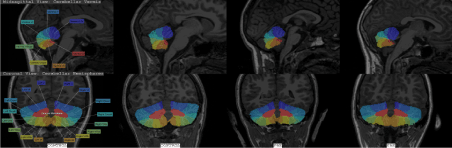
Figure 5. Coronal and sagittal sections from two PAE and two controls, with CATK2 parcel labels showing good fidelity of the CATK2 fits
Figure 6 shows the comparison between PAE and control adolescents for each of the CATK2 parcels with significant results indicated in green. For the hemispheres it shows lower cerebellar volumes. We found lower volumes for PAE vs. controls for left and right corpus medullare, CrusI and VIIb and for left VI, with a trend in the same direction for right VI. For the vermis, PAE had lower volumes for lobe V, with trends for reduced volumes for VIIIab and I-IV. The results provide insightful findings regarding the particulars of cerebellum involvement in the consequences of prenatal alcohol use and abuse and the behavioral phenomena seen in children with PAE.
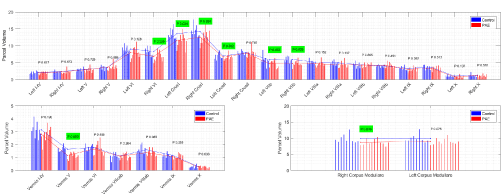
Figure 6. Comparison of CATK2 measures on 9 controls and 11 subjects with PAE
Since CATK2 models learn intrinsic features from manual labels, its reliability and validity is by definition limited by the reliability of the hand delineation of the cerebellar parcels. The reliability of the measure is essentially a ratio of the average variability within subjects of the estimates to the variability of the true measures across subjects on whom the assessment of reliability is performed. For example, where the reliability assessment performed on a group that included individuals with known cerebellar anomalies, the reliability would have been greater. This might have been related to the power of CATK2 to separate the PAE from normal children given the known differences between the groups, hence the larger denominator of the reliability ratio. The PAE results presented here are interesting in that the cerebellar segmentations show where in the cerebellar vermis and hemispheres the PAE effects are present. Reduced cerebellar volumes in PAE children are evident in regions involved in i-RISA component functions. Additionally, we show that the lower volume in the anterior superior vermis is specific to lobule V, and that PAE show reduced bilateral corpus medullare volumes. This may be associated with such children showing difficulty with executive control functions. However, the import of these results is tempered by the small sample sizes studied and the fact that actual alcohol use in the PAE sample was not studied.
We have presented a 29-parcel automated cerebellar segmentation algorithm (CATK2) based on hierarchical Bayesian Active Appearance Models. CATK2 was trained on 38 0.7mm3 motion-corrected T1-weighted images that were manually labelled by Neuromorphometrics, Inc.
The method performs an image registration between the image under consideration and template images, followed by the application of a hierarchical series of appearance models, and finally applies post-processing to generate voxel-wise label map of the underlying cerebellar lobules. The use of multiple pre-registration frameworks is possible: CATK2 uses 3D-SIFT and RANSAC for multi-template alignment, and also an alternative pipeline using ANTS for pre-alignment, which can be used for lower-resolution images that do not produce sufficient SIFT features.
Owing to the small number of unique subjects in the training data, leave-one-out validation was selected as the evaluation technique for assessing reliability and validity. CATK2 shows excellent repeatability in terms of test re-test ICC computed across multiple studies of the same subject. Promising results are also seen in the overall agreement between CATK2 and the manual labeled data in terms of dice overlap comparison. However, lower scores in ICC validity comparisons are seen due to the small volumes intrinsic to the use of a very detailed parcellation protocol. In addition, this is partially due to the lower agreement between the test re-test scans of the manual labelings which are used for training. Comparison of CATK2 ICCs for several image resolutions negligible loss of CATK2 test-retest reliability when applying CATK2 high-resolution models to standard resolution non motion-corrected data. Finally, when applied to samples of prenatal alcohol exposed and control children, CATK2 provided more precise analysis of where within the cerebellar the effects of prenatal alcohol exposure are evident. [33]
We would like to thank the NIAAA for their outstanding effort in refining the motion-correction acquisition protocol and for their support of this work (R43 AA021945, U01 AA014834).
- Schmahmann JD, Pandya DN (1992) The cerebrocerebellar system. Int Rev Neurobiol 41: 31-60. [Crossref]
- Schmahmann JD,Pandya DN (1995) Prefrontal cortex projections to the basilar pons in rhesus monkey: implications for the cerebellar contribution to higher function. Neurosci Lett 199: 175-178. [Crossref]
- D‘Angelo E, Casali S (2013) Seeking a unified framework for cerebellar function and dysfunction: from circuit operations to cognition. Front Neural Circuits 6: 116. [Crossref]
- Ito M (2006) Cerebellar circuitry as a neuronal machine. Prog Neurobiol 78: 272-303. [Crossref]
- Schmahmann JD (2004) Disorders of the cerebellum: ataxia, dysmetria of thought, and the cerebellar cognitive affective syndrome. J Neuropsychiatry Clin Neurosci 16: 367-78. [Crossref]
- Diamond A (2000) Close interrelation of motor development and cognitive development and of the cerebellum and prefrontal cortex. Child Dev 71: 44-56. [Crossref]
- Sullivan EV (2003) Compromised pontocerebellar and cerebellothalamocortical systems: speculations on their contributions to cognitive and motor impairment in nonamnesic alcoholism. Alcohol Clin Exp Res 27: 1409-1419. [Crossref]
- Goldstein RZ, Volkow ND (2002) Drug addiction and its underlying neurobiological basis: neuroimaging evidence for the involvement of the frontal cortex. Alcoholism Clinical and Experimental Research 159: 1642-1652. [Crossref]
- Goldstein RZ, Volkow ND (2011) Dysfunction of the prefrontal cortex in addiction: neuroimaging findings and clinical implications. Nat Rev Neurosci 12: 652-69. [Crossref]
- Volkow ND, Fowler JS, Wang GJ (2004) The addicted human brain viewed in the light of imaging studies: brain circuits and treatment strategies. Neuropharmacology 47: 3-13. [Crossref]
- Fein G, Cardenas VA (2015) Neuroplasticity in human alcoholism: Studies of extended abstinence with potential treatment implications. Alcohol Res 37: 125-141. [Crossref]
- O'Reilly JX (2010) Distinct and overlapping functional zones in the cerebellum defined by resting state functional connectivity. Cereb Cortex 20: 953-965. [Crossref]
- Chanraud S (2010) Dual tasking and working memory in alcoholism: relation to frontocerebellar circuitry. Neuropsychopharmacology35: 1868-1878. [Crossref]
- Chanraud S (2007) Brain morphometry and cognitive performance in detoxified alcohol-dependents with preserved psychosocial functioning. Neuropsychopharmacology. 32: 429-438. [Crossref]
- Shear PK (1996) Mammillary body and cerebellar shrinkage in chronic alcoholics with and without amnesia. Alcohol Clin Exp Res 20: 1489-1495. [Crossref]
- Sullivan EV, Rohlfing T, Pfefferbaum A (2010) Pontocerebellar volume deficits and ataxia in alcoholic men and women: no evidence for "telescoping". Psychopharmacology (Berl) 208: 279-90. [Crossref]
- Sullivan EV (2010) Pontocerebellar contribution to postural instability and psychomotor slowing in HIV infection without dementia. Brain Imaging Behav. 5: 12-24. [Crossref]
- Sullivan EV (2000) Cerebellar volume decline in normal aging, alcoholism, and Korsakoff's syndrome: relation to ataxia. Neuropsychology. 14: 341-352. [Crossref]
- Buckner RL (2011) The organization of the human cerebellum estimated by intrinsic functional connectivity. J neurophysiol 106: 2322-2345. [Crossref]
- Habas C (2009) Distinct cerebellar contributions to intrinsic connectivity networks. J Neurosci 29: 8586-8594. [Crossref]
- Krienen FM, Buckner RL (2009) Segregated fronto-cerebellar circuits revealed by intrinsic functional connectivity. Cereb Cortex 19: 2485-2497. [Crossref]
- Kelly RM, Strick PL (2003) Cerebellar loops with motor cortex and prefrontal cortex of a nonhuman primate. Journal of neuroscience 23: 8432-8444. [Crossref]
- Benegal V (2007) Gray matter volume abnormalities and externalizing symptoms in subjects at high risk for alcohol dependence. Addiction Biology 12: 122-132. [Crossref]
- Hill SY (2007) Cerebellar volume in offspring from multiplex alcohol dependence families. Biol Psychiatry 61: 41-47. [Crossref]
- Sowell ER (2008) Abnormal cortical thickness and brain-behavior correlation patterns in individuals with heavy prenatal alcohol exposure. Cereb Cortex 18: 136-144. [Crossref]
- Sowell ER (1996) Abnormal development of the cerebellar vermis in children prenatally exposed to alcohol: size reduction in lobules I-V. Alcohol Clin Exp Res 20: 31-34. [Crossref]
- Hill SY (2011) Cerebellum volume in high-risk offspring from multiplex alcohol dependence families: association with allelic variation in GABRA2 and BDNF. Psychiatry Res 194: 304-313. [Crossref]
- De Bellis M.D (2005) Prefrontal cortex, thalamus and cerebellar volumes in adolescents and young adults with adolescent onset alcohol use disorders and co-morbid mental disorders. Alcohol Clin Exp Res. 29: 1590-1600 [Crossref]
- Diedrichsen J (2006) A spatially unbiased atlas template of the human cerebellum. Neuroimage 33: 127-138. [Crossref]
- Bogovic JA, Prince JL, Bazin PL (2013) A multiple object geometric deformable model for image segmentation. Comput Vis Image Underst 117: 145-157. [Crossref]
- Patenaude B (2011) A Bayesian model of shape and appearance for subcortical brain segmentation. Neuroimage 56: 907-922. [Crossref]
- Price M, Cardenas VA, Fein G (2014) Automated MRI cerebellar size measurements using active appearance modeling. Neuroimage 103: 511-521. [Crossref]
- Cardenas V (2014) Automated cerebellar segmentation: Validation and application to detect smaller volumes in children prenatally exposed to alcohol. NeuroImage: Clinical 4: 295-301. [Crossref]
- Sharma N, Aggarwal LM (2010) Automated medical image segmentation techniques. J Med Phys 35: 3-14. [Crossref]
- Dale AM, Fischl B, Sereno MI (1999) Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 9: 179-194. [Crossref]
- Talairach J, Tournoux P (1988) Co-planar stereotaxic atlas of the human brain: 3-Dimensional proportional system: An approach to cerebral imaging. Alcohol Clin Exp Res. 122.
- Mazziotta J (2001) A probabilistic atlas and reference system for the human brain: International Consortium for Brain Mapping (ICBM). Philos Trans R Soc Lond B Biol Sci 356: 1293-1322. [Crossref]
- Mazziotta JC (1995) A probabilistic atlas of the human brain: theory and rationale for its development. The International Consortium for Brain Mapping (ICBM). Neuroimage 2: 89-101. [Crossref]
- Ashburner J (2007) A fast diffeomorphic image registration algorithm. Neuroimage 38: s95-113. [Crossref]
- Avants BB (2008) Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med image anal 12: 26-41. [Crossref]
- Yeo, BT (2009) Spherical demons: fast diffeomorphic landmark-free surface registration. IEEE transactions on medical imaging. 29: 650-668. [Crossref]
- Penny WD (2011) Statistical parametric mapping: The analysis of functional brain images. Academic Press.
- Powell S (2008) Registration and machine learning-based automated segmentation of subcortical and cerebellar brain structures. Neuroimage 39: 238-247. [Crossref]
- Dolz J, Desrosiers C, Ayed IB (2018) 3D fully convolutional networks for subcortical segmentation in MRI: A large-scale study. NeuroImage 170: 456-470. [Crossref]
- Roy AG (2018) Quicknat: Segmenting mri neuroanatomy in 20 seconds. arXiv:1801.04161.
- Balakrishnan G (2019) VoxelMorph: a learning framework for deformable medical image registration. IEEE transactions on medical imaging.
- Kass M, Witkin A, Terzopoulos D (1988) Snakes: Active contour models. Int j comp vis 1: 321-331.
- Hwang J (2011) An automatic cerebellum extraction method in T1-weighted brain MR images using an active contour model with a shape prior. Magn Reson Imaging. 29: 1014-1022. [Crossref]
- Cootes T (2000) An introduction to active shape models, in image processing and analysis, Oxford University Press: Oxford.
- Cootes TF, Edwards GJ, Taylor CJ (2001) Active appearence models. transactions on pattern analysis and machine intelligence 23: 681-685.
- Babalola K, Cootes T (2010) Using parts and geometry models to initialise active appearance models for automated segmentation of 3d medical images. in 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2010.
- RP W (1998) Automated image registration: I. General methods and intrasubject, intramodality validation. J Comput Assist Tomogr 22: 139-152. [Crossref]
- RP W (1998) Automated image registration: II. Intersubject validation of linear and nonlinear models. J Comput Assist Tomogr 22: 153-165. [Crossref]
- Avants BB (2014) The Insight ToolKit image registration framework. Front neuroinfor 8: 44. [Crossref]
- Bloomenthal J (1994) Olv. 8. Graphics gems IV4: 324.
- Moenning C, Dodgson NA (2003) Fast marching farthest point sampling for implicit surfaces and point clouds. Computer Laboratory Technical Report 565: 1-12.
- Rister B (2015) Scale- and orientation-invariant keypoints in higher-dimensional data. IEEE International Conference on Image Processing (ICIP) pp: 3490-3494.
- Dice LR (1945) Measures of the amount of ecologic association between species. Ecology 26: 297-302.
- Jones KL (2006) Accuracy of the diagnosis of physical features of fetal alcohol syndrome by pediatricians after specialized training. Pediatrics 118: e1734-e1738. [Crossref]
- Mattson SN (2010) Collaborative initiative on fetal alcohol spectrum disorders: methodology of clinical projects. Alcohol 44: 635-641. [Crossref]






