Take a look at the Recent articles

Abstract

Based on my study of cholera and mental illness, in particular, schizophrenia, I’ve discovered some mathematical laws that to apply to epidemiology. It is the familiar “Robust Solution” that I’ve developed in other papers on physics and economics.  The same math applied in the study of the transmission and termination of contagious disease What I provide here is mathematics from the Robust solution that applies to epidemiology.

Key words

epidemiology, Gaussian distribution

Introduction

We consider conditional probability, the Gaussian distribution, Overcrowding, resistance to disease, the golden mean below. We develop a basic law of contagion.

Conditional probability

Gaussian distribution

Overcrowding resistance to disease, and the Golden Mean parabola:

Cusack’s Contagion Law

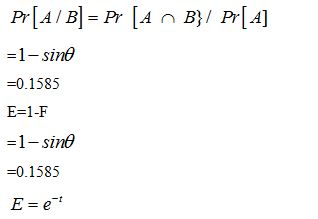
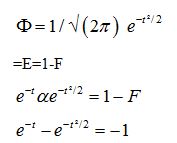
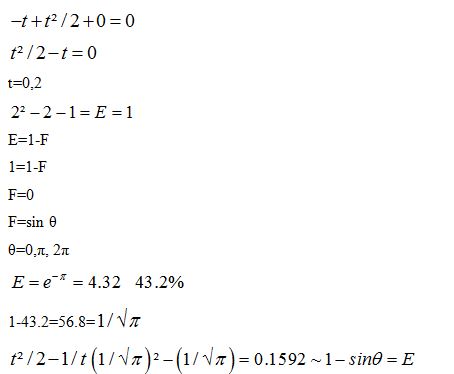
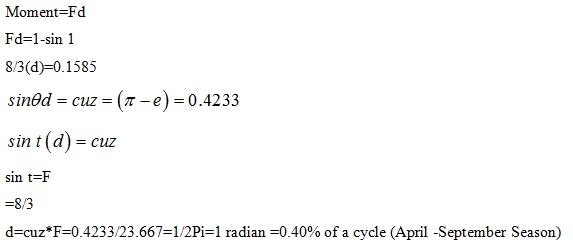
Infected *d=Resistance to infection

Probabilities and the Contagion

Conclusion

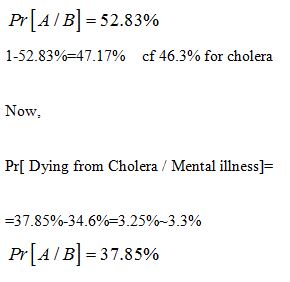
So we see that the Robust solution mathematics applies to Epidemiology as well as it applies to any two pole problem, under which lies the Gaussian distribution.

References

1. Somerville GF (1854) Saint John and Portland cholera Deaths. Saint John, NB
2. Bislon G (1854) The Cholera Epidemic in Saint John, NB Acadiensis 
3. Weiss NA (2008) Introductory Statistics, 8th Ed. Pearson, Addison Wesley, USA.
4. Cusack P (2015) Sz and Its Cause., LULU.
5. Cholera and Mental Illness, Mental health, Family Medicine
6. Iron, Cholera, and Mental illness in Nineteenth-Century Saint John. Clinical Investigation and Medical Research, OMI