Take a look at the Recent articles

Abstract

Introduction and objective:  In 1886, Starling proposed a hypothesis for the capillary–interstitial fluid (ISF) transfer, in which the capillary was thought a tube of a uniform diameter that is impermeable to plasma proteins. The flow of fluid across its wall was thought dependent upon a balance between the hydrostatic pressure within its lumen causing ‘filtration’, and the osmotic pressure of plasma proteins causing ‘absorption’. The physical basis on which LP of a capillary was thought positive and responsible for filtration was Poiseuille’s work on long Brass tubes of uniform diameters. Later discoveries demonstrated that the capillary is a porous orifice tube with totally different hydrodynamics that is reported here.

Material and methods: The hydrodynamics of an inlet tube was studied in order to demonstrate the negative side pressure (SP) gradient exerted on its wall. We then studied the porous orifice (G) tube akin to capillary and later enclosed it in a chamber (C), akin to interstitial fluid space, making the G-C apparatus demonstrating the G-C circulation phenomenon. The effect of proximal (arterial) pressure (PP), distal (venous) pressure (DP) and inlet diameter on the SP and CP of the G-C model are reported.

Result: The PP induces the negative SP in the G tube which is responsible for absorption. The orifice has an inverted bell shaped effect on SP and CP. The DP augments filtration. The G tube enclosed it in a chamber (C), making the G-C apparatus demonstrating the G-C circulation phenomenon.

Conclusion: Hydrodynamic studies on G tube, based on capillary ultrastructure, demonstrate results which differ from Poiseuille’s in a strait tube, challenge the role attributed to arterial pressure as a filtration force in Starling’s hypothesis. A perspective literature review shows that the oncotic pressure force has been previously cancelled and the Starling’s hypothesis has failed to explain the capillary–ISF transfer in most parts of the body.

A concept based on a new hydrodynamic of the G-C model phenomenon is proposed for the capillary–ISF circulation. An autonomous dynamic magnetic field-like G–C circulation occurs between fluid in the G tube’s lumen and a surrounding fluid compartment C. Based on results of studies on a circulatory model incorporating the G–C apparatus, factors which initiate, regulate and affect the G–C circulation, its physiological and haemodynamic relevance and its clinical importance to the pathogenesis of oedema and shock are discussed.

Key words

Capillary circulation, Starling’s law, Capillary interstitial fluid transfer, Hydrodynamic, Shock, Hyponatraemia (HN), the transurethral prostatectomy syndrome (TURS), the adult respiratory distress syndrome (ARDS)

Abbreviations

VO: Volumetric overload; VOS: Volumetric overload shocks; VOS1: Volumetric overload shock, Type 1; VOS2: Volumetric overload shock, Type2; TURS:  The transurethral resection of the prostate syndrome; ARDS: The adult respiratory distress syndrome; MVOD/F: The multiple vital organ dysfunction/ failure syndrome; HN: Hyponatraemia; BP: Arterial Blood pressure; CVP: Central venous pressure;  PV: Plasma volume; ISF:       Interstitial fluid volume; G Tube: The Porous Orifice Tube;  PP: Proximal pressure to the G tube akin to arterial Blood pressure; DP: Distal Pressure to the G tube akin to venous pressure; LP: Lumen pressure of the G tube; FP: Flow pressure is the positive pressure inside the G Tube; SP: Side pressure is the negative pressure inside the G Tube

Introduction

In 1886, Starling proposed a hypothesis for the capillary–interstitial fluid (ISF) transfer [1], in which the capillary was thought a tube of a uniform diameter that is impermeable to plasma proteins. The flow of fluid across its wall was thought dependent upon a balance between the hydrostatic pressure within its lumen (Pc), encouraging fluid to leave ‘filtration’, and the osmotic pressure of plasma proteins (pc), tending to draw fluid back to the capillary lumen ‘absorption’, with similar opposing smaller forces in the ISF space. At the arterial end of the capillary, lumen pressure (LP) is greater than the oncotic pressure and fluid is pushed out. At the venous end, osmotic pressure is higher and fluid is withdrawn into capillary lumen.

The physical basis on which LP of a capillary was thought positive and responsible for filtration was Poiseuille’s work (1799–1869) on long Brass tubes of uniform diameters [2]. However, Burnoulli’s effect of a fluid jet and Venturi’s effect of a tube constriction are well known and must also be considered to be of significance even under laminal flow conditions. LP refers to the arterial pressure of a capillary.

Starling’s hypothesis has undergone extensive evolution to become a law prior to discovery of the capillary ultra-structure of the pre-capillary sphincter and its porous wall plus the osmotic chemical composition, negative pressure and dynamics of ISF and lymph [3-7]. Inadequacy in explaining the capillary–ISF transfer in many parts of the body [8], particularly vital organs, has previously called for reconsideration of Starling’s law [8,9].

In 1984, clinical observations inconsistent with Starling’s hypothesis prompted =physical and clinical studies [10-12] to verify LP and fluid dynamics in a porous orifice (G) tube with reference to the effect of the pre-capillary sphincter, arterial and venous pressures on the capillary–ISF transfer. The observation was: during hypotension shock in which prompt and adequate vascular expansion for resuscitation, all fluids leaked into and drowned the ISF space and filled the potential body cavities, demonstrated on post-mortem examination!

The questions and logic

This observation, augmented with another that although arterial hypertension is very common it does not cause oedema, posed the questions: If LP is a filtering force in the capillary, how such massive fluid was filtered into ISF space during hypotension? Is LP truly responsible for filtration and, if not, what is? The logic that followed was that: if Dr Starling had based his hypothesis on Poiseuille’s results of physical experiments, similar studies on tubes built on a scale to the capillary ultrastructure, i.e the G tube, should answer the questions.

Perspective review of capillary physiology

Folkow and Neil [2], stated that: ‘The greatest discovery in medical science was made by William Harvey, who showed in 1628 that the heart pumped the blood around the circulatory system and understood that the circulation provided nourishment for the tissues’. Four centuries earlier, however, Ebn Al-Nafis (1210–1298), discovered the pulmonary circulation. Both the systemic and pulmonary circulations exist to provide for tissues’ viability. Capillary circulation is directly responsible for this vital function in every organ and tissue.

In 1886, Starling, a great physiologist, proposed a hypothesis for the capillary–ISF exchange. It was based on two known physical forces; LP based on Poiseuille’s tube as a filtration force and the oncotic pressure as a reabsorption force [1]. In 1929, Landis measured LP of a capillary, by a cannula facing up stream, which was 32 and 12 mmHg at the arterial and venous ends, respectively [13].

In 1948, Pappenheimer and Soto-Rivera studied the quantitative changes in the weight of isolated hind limbs of dogs induced by alterations of the arterial and venous pressures [14]. Oedema was induced by increasing the venous pressure in order to match any increase in the arterial pressure (mmHg for a mmHg). Such, ‘isogravimetric state’, in which capillary filtration exceeds absorption, as would be expected with high venous pressure, was thought in support of Starling’s hypothesis. The authors also found that the osmotic pressure of a concentrated plasma solution was 23–28 mmHg in vitro. Ever since, most physiologists have accepted Starling’s hypothesis as a physiological law.

However, most of the enlightening scientific evidence on microcirculation started to appear decades later. In 1960, Mellander [15] showed that ISF ‘absorption’ increased after autonomic stimulation, which narrows the lumen of ‘microvessels’ and pre-capillary sphincter, and increases arterial pressure. In 1962, Hendry measured the oncotic pressure of various body fluids and found it identical to that of the plasma, pointing out: ‘the osmotic pressure of plasma proteins is too weak a force to return fluids back into the capillary lumen’ [5]. In 1963, Guyton and Colman measured ISF tissue pressure, using an implanted perforated capsule, and found that it has a negative value of –7 cm water [6].

In 1972, Calnan et al. confirmed this finding and showed that molecules, including plasma proteins, pass freely and rapidly between the capillary blood and the implanted capsule, and vice versa [7]. In 1967, Rhodin showed that the capillary tube is encircled by a cuff of smooth muscle fibres at its arteriolar junction, named the pre-capillary sphincter (3–5 mm), which is the narrowest part of the whole vascular system [3]. Also in 1967, Karnovesky showed that the capillary wall is made of flat cells and their intercellular junctions are slits 10 to 20 nm wide which are the pores through which fluids, nutrients and protein molecules pass freely [4]. His photographs show the stained horse radish globules, which are much larger than plasma protein molecules, passing through these pores. The findings concerning plasma proteins and capillary pores alone, has cancelled the absorption force in Starling’s hypothesis. After all, plasma proteins’ main function, like blood glucose, must be a nutrient material for the cells.

In 1983, Mattfeldt and Mall reported the ultrastructure dimensions of capillaries. The ‘ideal’ capillary is a tube connecting an arteriole to a venule [16]. According to Crogh’s model it is a perfect, anisotropic, straight and un-branched tube with a diameter of 7–18 mm. The pre-capillary sphincter and intercellular slits make the capillary a strait ‘porous orifice tube’, based on which the G tube was made on a larger scale.

In 1982, Keele, Neil and Joels, pointed out that the concentration of tissue proteins in the liver, lung and muscles is 60% that of plasma proteins [8]. In the pulmonary circulation, arterial pressure is less than the plasma oncotic pressure. Thus, fluid filtration in the lungs and reabsorption in the liver and muscles lacks explanation. The oncotic pressure neither can explain the negative pressure in ISF space nor the speed and efficiency with which the capillary–ISF fluid, nutrients and oxygen transfer occurs [6]. Lymph drainage cannot explain the negative ISF pressure either [6,7]. This knowledge on capillary ultrastructure and permeability to macromolecules, prompted Renkin (1986) to call for reconsideration of Starling’s hypothesis but an alternative mechanism was still evolving at that time which is reported here [9].

Material and methods

We studied the hydrodynamics of a rubber inlet tube in order to demonstrate the negative side pressure (SP) gradient exerted on its wall as well as the flow pressure (FP) components of its lumen pressure (LP). We then studied the porous orifice (G) tube akin to capillary and later enclosed it in a chamber (C), akin to interstitial fluid space, making the G-C apparatus demonstrating the G-C circulation phenomenon.

The factors affecting the speed and efficiency of the G-C circulation were evaluated. These included the proximal (PP), the distal pressure (DP) and the inlet diameter (r) as a relation to the tube diameter (R). The G-C apparatus was enclosed in a circulatory model driven by electrical pump and connected to manometers for evaluating the hydrodynamics of the circulatory model.

Results

The hydrodynamics of a rubber inlet tube that demonstrates the negative side pressure (SP) gradient exerted on its wall as well as the flow pressure (FP) components of its lumen pressure (LP) is shown in Figure 1. A graph showing FP and SP gradients is shown in Figure 2. The hydrodynamics of the G tube is shown in Figure 3. The G-C phenomenon is shown in Figure 4. The relation of PP to SP and CP is shown in Figure 5. The relation of Orifice diameter to SP and CP is U shaped or inverted Bell shaped, and is shown in Figures 6 and 7. The relation of DP to SP and CP is shown in Figure 8. The pressure gradient observed and measured at various points in the G- C circulatory model is shown in Figure 9. Figure 10 shows a circulatory model incorporating the G-C apparatus with manometers measuring various pressures.

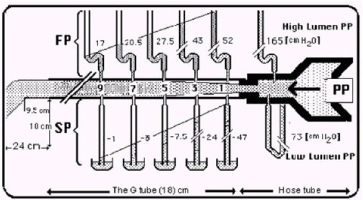
Figure 1. shows the lumen pressure (LP) components of flow pressure (FP) and side pressure (SP) of a rubber orifice tube as measured by manometers with needles inserted at various cm distances from the inlet. When the needle’s bevel faces upstream it measures FP (Top manometers) and when acing downstream it measures SP (Bottom manometers).

Figure 2. is a graph showing the FP and SP components of LP of the G Tube at CM distances rom the inlet.

Figure 3. shows the hydrodynamic of a porous oriice (G) tube. The side pressure (SP) gradient exerted on its wall turns from negative near the inlet to positive near the exit. The magnetic field like G-C circulation is shown when the tube is placed in a surrounding chamber.

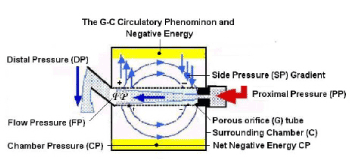
Figure 4. shows a diagram o the G-C circulation creating a net negative pressure in C (Highlighted in yellow).

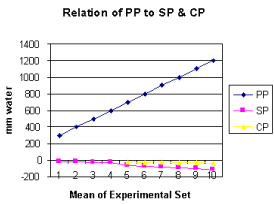
Figure 5 shows the relation of proximal pressure (PP) to side pressure (SP) and chamber pressure (CP). A high PP enhances suction negativity of SP and CP.

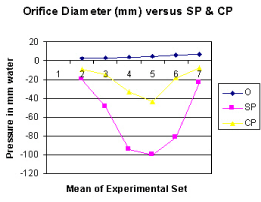
Figure 6. shows the relation of orifice diameter to side pressure (SP) and chamber pressure (CP).

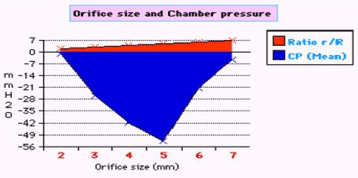
Figure 7. shows the relation of orifice ratio to tube diameter on CP.

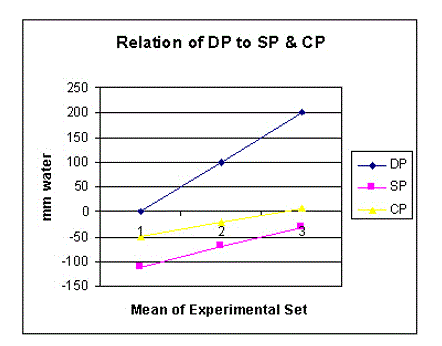
Figure 8. shows the relation of distal (venous) pressure (DP) to side pressure (SP) and chamber pressure (CP).

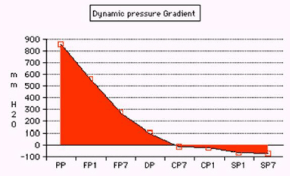
Figure 9. shows the pressure gradient from proximal pressure (PP) to flow pressure (FP) inside the G tube at points 1 and 7 to distal venous pressure (DP) then chamber pressure (CP) and side pressure (SP) at points 1 and 7.

Figure 10. shows a circulatory model incorporating the G-C apparatus with manometers measuring PP, CP at points 1 and 7 and DP. Note that CP is lower than DP.

It is observed from the presented results that the hydrodynamics of the G tube is totally different from Poiseuille’s tube. The orifice of the G tube creates a negative pressure gradient on its wall inducing a suction force which is transmitted to the surrounding chamber C creating a dynamic magnetic field like fluid G-C circulation that rapidly irrigates the C. The orifice thus transfers the PP from a filtration force in Poiseuille’s tube into a suction force in the G tube. Increasing the PP enhances the G-C circulation while reducing it slows it down as shown in Figure 5. The distal pressure has the opposite effect. Increasing the DP slows down the G-C circulation and turns the pressure in C into positive with increased volume. The effect of increasing the orifice diameter has U or inverted Bell shaped effect on SP and CP Figure 6. The G-C circulation thus offers a complete and correct replacement for Starling’s law. The circulatory model Figure 10 has remarkable similarity to the circulatory vascular system.

Discussion

Relevance of physical data to physiological evidence

Results of studies on the G tubes would make sense when linked to its physiological and haemodynamic equivalents. PP akin to ‘arterial’ pressure induces a flow jet with its LP components. The negative energy SP component occurs maximally over the proximal part of the G tube (Figure 1), and is mainly responsible for suction akin to ‘capillary absorption’. Filtration occurs autonomously over the distal part of the tube (Figures 1 and 2). Both effects induce the G–C circulation phenomenon (Figure 3). SP also induces a net negative energy pressure in chamber C (Figure 4), demonstrated by the caving in of a membrane cover. A net negative CP is akin to the negative pressure of ISF and subcutaneous spaces [6,7]. Although fluid comes out autonomously through the distal holes of the G tube, it is greatly augmented by increasing the outflow DP akin to elevating venous pressure, augmenting ‘filtration’ and causing ISF shift or oedema.

The G-C circulation phenomenon causes rapid mixing of fluids in the lumen of the G tube and a surrounding fluid chamber compartment C (Figure 4). Its efficiency in exchanging materials between the G tube and chamber C, akin to ‘capillary and ISF compartments’ is remarkable. A few small G tubes contained in chamber C have commutative effect. The shape of pores, whether hole or slit makes no difference. Large particles trapped in chamber C require regular cleaning. The negative energy of the G–C circulation is a considerable force. This negative energy force effectively irrigates chamber C, allowing rapid transfer of fluid and particles into and from chamber C, akin to the passage of fluids with ‘oxygen and nutrients including protein molecules into the ISF space and washing out waste products while preventing excess ISF accumulation. Guyton and Coleman’s capsule provided excellent evidence on the negative energy pressure of the ISF induced by the dynamic capillary flow, as demonstrated by the net negative CP in the G–C apparatus (Figure 4) [6].

Forces initiating and regulating the g–c circulation

The G–C circulation, SP and negative CP are initiated and regulated by PP, orifice and DP. Changes which slow down the G–C circulation by decreasing the negative energy pressures of SP and CP are akin to that inducing shock and ISF shift. Changes which enhance the speed, augments its efficiency in fluid exchange akin to meeting increased physiological demands.

Increasing PP causes greater suction effect and rapid G–C circulation by augmenting the negative energy of SP and CP (Figure 5). This is akin to arterial pressure keeping ISF space almost ‘dry’ while effectively irrigated, ventilated and nourished under basic physiological conditions and autonomic stimulation during exercise. Decreasing PP, akin to arterial hypotension, decreases the jet speed, diminishes its negative SP and slows down the G–C circulation. Fluid stagnation and increased CP in chamber C occurs ‘CP moves towards 0 or becomes positive’. This is akin to inducing both shock and shift of circulatory fluid into the ISF space.

The role of the orifice or ‘precapillary sphincter, in collaboration with PP or arterial pressure’, is fine tuning the G–C, akin to capillary–ISF circulation, respectively. The orifice is not only responsible for most of the peripheral resistance maintaining PP akin to arterial pressure but is also the dynamo regulating the G–C circulation akin to the capillary– ISF circulation. Maximum negative SP energy with a most speedy and efficient G–C circulation is demonstrated when the orifice/tube diameter ratio is 0.7, the equivalent to orifice/tube area ratio of 0.5. The relation of the orifice diameter to the negative SP and CP is inverted Bell shaped (Figures 6,7). Adequate G–C circulation is preserved at high efficiency at a wide variation of PP through minor adjusting changes of the orifice or ‘precapillary sphincter’ diameter. Thus, adrenergic stimulation, which narrows the precapillary sphincter and elevates arterial pressure, increasing ISF fluid absorption may be simulated by changing orifice diameter in the G–C circulation. Extreme changes of the orifice, too wide or narrow, alter the G–C circulation [15,16].

Removing the orifice makes the tube a Poiseuille’s tube with positive pressure gradient. Too narrow orifice prevents flow and slows down the G–C circulation akin to tissue ischaemia. The autonomic tuning of precapillary sphincters is better known for effects on arterial pressure but it is also important in regulating capillary–ISF circulation and tissues’ viability [15]. Its dilatation causes hypotensive syncope or anaphylactic shock while severe constriction causes hypertension with tissue ischaemia. This indeed suggests that the precapillary sphincter is the master of both systemic and capillary circulations.

DP is always higher than CP (Figures 8-10) and both are proportionally and closely related. When DP is 0, CP is sub-atmospheric. Elevating DP or ‘venous’ pressure, increases CP and volume of fluids in chamber C, akin to drowning the ‘ISF’ space and inducing oedema. Such evidence is consistent with the known fact that high ‘venous’ pressure is primarily responsible for filtration, increased fluid shift into the ISF space and dropsy formation.

Relevance of hydrodynamics of the G-C circulatory model to haemodynamic

Analysis of the forces which initiate and regulate the G–C circulation with reference to its haemodynamic equivalents is best demonstrated by comparing the dynamics of PP, DP and CP of the G–C apparatus incorporated in a circulatory model (Figure 10). Before starting the pump an adequate volume of fluid induces a hydrostatic equilibrium in all manometer tubes. Running the pump induces the dynamic pressure values in the manometers. In (Figure 10), PP = 650 and DP = 12 while CP had values of 8–10 mm waters at points 1 and 2 in chamber C. Fluid in chamber C flows from point 2 to point 1, in an opposite direction to flow in the G–C circulatory system model, shown by injecting ink into chamber C. Adding more fluid to the system mimicking VO or vascular expansion increases venous pressure and CP.

This means that increasing DP elevates CP and increases fluid volume in chamber C by a proportional amount of hydrostatic pressure. A pressure gradient remains between DP, CP2 and CP1, allowing fluid movement down it. Massive VO of the system model increased fluid volume and CP in chamber C, which decreased the negative energy SP and slowed down significantly the G–C circulation. Most interestingly, such VO also reduced PP.  The injected ink into chamber C moves very slowly in the opposite direction to fluid flow in the G–C circulatory system. Volumetric expansion until DP, CP and PP attain hydrostatic equilibrium, ceases the G–C circulation even while the pump is operating. This may mimic a pathological haemodynamic circulatory condition (vide infra).

In the G–C circulatory model, also decreasing PP eventually abolished the dynamic pressure forces and restores fluid hydrostatic equilibrium in manometers. This elevates DP, CP and fluid volume in chamber C which slows down the G–C circulation. This is akin to shock, inducing ISF shift and causing tissue hypoxia. It may be of practical significance in differentiating types of shock and deciding on its optimum fluid therapy.

Pitfalls of starling’s hypothesis

Dr Starling proposed his hypothesis 80 years prior to the discovery of the precapillary sphincter [3] and the slit pores of the capillary wall [4] which are permeable to macromolecules and plasma proteins [4,5,7,9]. The hypothesis has failed to explain the capillary–ISF transfer in most parts of the body [8]. For the oncotic pressure to work an impermeable membrane to plasma proteins must exist but it does not. For the capillary to work on the basis of a positive pressure gradient of Hagen–Poiseuille’s tube, which causes filtration all along the tube, another force must exist for reabsorption, and there is none. It neither explains Guyton and Colman’s discovery of the negative ISF pressure [6] nor how venous obstruction or pressure elevation causes oedema while arterial hypertension never does.

The measured LP of the capillary tube by Landis [13] is akin to measuring FP in the G tube. At that time, there was no distinction between the components of a dynamic flow, as presented here. LP of the capillary was thought responsible for filtration and its elevation was thought possible by elevating venous or arterial pressures-alike, as demonstrated by the isogravimetric experiments done by Pappenheimer and Soto-Rivera [14].

Clinical observations and evidence, though affirm that elevating venous pressure does increase filtration and cause oedema, elevating arterial pressure does not have such effect but on the contrary, it increases absorption.

Not only that, an increase in venous pressure has an opposite effect to arterial pressure on capillary filtration but also its augmentation of filtration far exceeds the effect of an equal increase in arterial pressure on reabsorption. More importantly, is that the hypothesis represents the basis on which clinical decisions for fluid therapy are made, both in the cardiovascular (CVS) resuscitation of shock, burns and in the management of the acutely ill, trauma and surgical patients. Dynamic monitoring of central venous pressure (CVP) and arterial pressure, with reference to capillary circulation, dictate the rules on fluid therapy has undoubtedly proved its value in saving millions of civilian and military lives suffering from haemorrhagic and hypovolaemic shocks, in which cases the rules do work well.

Such rules, however, fail miserably when vascular expansion is indiscriminately used to elevate CVP and pulmonary capillary wedge pressure (PCWP) to high un-physiological levels of 15 and 18 mmHg, respectively. Received thinking that elevating CVP is synonymous with elevating arterial pressure is prevailing in current clinical practice during fluid therapy for shock and the management of the acutely ill patients. This is undoubtedly correct during restoration therapy for hypovolaemic and haemorrhagic shock. But, vascular expansion or VO is a different issue. Persistent attempts to elevate CVP and PCWP up to levels of 15/18 mmHg are commonly received but mistaken practice. The normal CVP is around 0 and most textbooks report a range of –7 to +7 cm water [17].

The pointed out clinical observations demonstrate that, in addition to the well-known effect of high venous pressure causing oedema, arterial hypertension has no such effect, if not the exact opposite. In clinical practice, although arterial hypertension is common, ISF oedema is unknown among its complications. In the G–C model, a minor increase in DP increases fluid volume in chamber C, reverts its CP from negative to positive while slowing the G–C circulation (Figures 6–8). Increasing DP has similar effects to decreasing PP on the G–C circulation and chamber pressure and volume. Vascular expansion causes VOS [18,19]. The pathological effects of vascular VO have been overlooked for various reasons [18]. Perhaps, because the above reported sophisticated components of a dynamic flow were unknown. Hypotension is always thought synonymous with hypovolaemia. Yet, vascular expansion may not elevate arterial pressure and at times, it aggravates hypotension [18-20]. The maximal capacitance of an adult’s CVS is about 7 litres [17] and any excess VO overflows into the ISF space, causing flooding and drowning. Thus, both hypovolaemia and hypervolaemia of 2 litres have pathological haemodynamic effects. Understanding the correct mechanism of the capillary–ISF transfer in relation to CVS volume, capacitance and dynamic pressures in regulating a physiological capillary–ISF circulation is clinically important. It is relevant to the management of ISF shift, oedema, shock and the MVOD/F syndrome [18-20].

The G–C phenomenon as a concept for capillary–isf circulation hypothesis

Well documented physiological studies though have contributed to the evolution of Starling’s hypothesis, has itself provided evidence for reconsideration but a mechanism for an alternative hypothesis was previously lacking. The autonomous magnetic field-like G–C circulation is the concept proposed as a mechanism for a new capillary–ISF hypothesis. One appreciates the considerable differences between physical experiments and the biological situation in vivo.

The speed and autonomy of the G–C circulation, under similar ranges of dynamic pressures of a human circulatory system, can truly explain the efficiency of capillary– ISF circulation in transporting oxygen and nutrients into cells while removing carbon dioxide and metabolites from tissue space. It should work in every part and organ of the body under both physiological and pathological conditions.

The results of hydrodynamic studies on the G tube, chamber C and G–C circulation are in perfect agreement with the summarized physiological evidence on the capillary ultrastructure, interstitial fluid and the capillary–ISF circulation. It also explains the changes responsible for the pathogenesis of oedema and shock which are the main capillary dysfunctions from a clinical point of view [18-20]. The lymphatic system cleans the ISF space from coarse particles and fat globules.

Apart from suggesting that fluid flows in at the arterial end and out at the venous end, through the wide slit pores of the capillary wall, the reported results also suggest that both the absorption and filtration are autonomous. Venous pressure rather than arterial pressure, affects filtration while reabsorption is the primary effect of arterial pressure and orifice or ‘precapillary sphincter’. This explains the observation that arterial hypertension, though common, never causes oedema while an increase in venous pressure does. It is in agreement with the results of physiological studies. More importantly, it may resolve the puzzle of the MVOD/F syndrome [18-20].

  Clinical relevance of the G-C circulation concept

2021 Copyright OAT. All rights reserv

The high incidence of the MVOD/F syndrome affecting postsurgical and trauma patients with its high morbidity and mortality [18-20] is a subject of increasing international attention and anxiety. Although, the role of microcirculation in its pathophysiology is recognized, its aetiology has remained elusive and the possible role of haemodynamic pressures and VO in its pathogenesis has been overlooked but has been recently reported [18-20]. VO shocks in which vascular expansion, aimed at correcting arterial hypotension by elevating CVP and PCWP to levels up to 15 and 18 mmHg, may culminate into the MVOD/F syndrome [11,18-20]. Massive fluid shift drowns the ISF and/or intercellular spaces, depending on fluid type.

The transurethral resection (TUR) of the prostate syndrome (TURS) is induced by massive sodium-free fluid (VO1), induced mostly by irrigant absorption during endoscopic surgery. The diluted serum solutes are good serum markers, characterized by the dilution hyponatraemic encephalopathic coma among features of the MVOD/F syndrome. The main haemodynamic disturbance of VO1 is hypotensive shock with interstitial fluid shift initially and intracellular fluid shift later [11,18-20]. Despite the massive VO, the patient suffers from severe irreversible hypotension shock and appears hypovolaemic. Ironically and misleadingly, this shock induced by massive VO1 calls for further vascular expansion! Electrolyte-based fluids (VO2) are commonly used to combat this shock. It transfers VOS1 into VOS2, erases serum markers and causes internal drowning while establishing the MVOD/F syndrome [18-20]. Such situation may also complicate the management of any type of the recognized shocks using any type of VO2 fluids.

An identical situation can be reproduced using the G–C circulatory model system. A combination of low PP and high DP causes the G–C circulation to become extremely slow or ceases (Figure 10). It is relevant to appreciate that factors which slow down the G–C circulation are similar to those causing shock and tissue hypoxia in clinical practice. A drop-in PP, extreme changes of orifice size and an increase in DP slow down the G–C circulation and increase fluid volume and CP, akin to ‘shock’ and ‘ISF shift’ of the MVOD/F syndrome.

Although an adequate circulatory volume and pressure is essential for a physiological capillary–ISF fluid circulation, VO just like hypovolaemia, causes serious haemodynamic disturbance. A persistent attempt to elevate CVP to a non-physiological level of 15/18 mmHg causes VO shock and drowning of the ISF and/or intercellular spaces. VO may paradoxically make a shock irreversible. Depending on the type of fluid inducing VO, a drop-in serum solute concentrations such as sodium and/or albumin may or may not occur. Further physical and physiological studies in which fluid flow in porous orifice tubes is integrated with capillary membranes, under physiological and pathological conditions are required. It is feasible to identify the exact aetiology of the MVOD/F syndrome, reduce its incidence among postsurgical and shock patients, find a current successful therapy [18-20] or devise future effective drugs.

Conclusion

Hydrodynamic studies on a porous orifice (G) tube, based on capillary ultrastructure, demonstrate results which differ from Poiseuille’s in a strait tube and hence challenge the role attributed to arterial pressure as a filtration force in Starling’s hypothesis. A perspective literature review shows that the oncotic pressure force has been previously cancelled and the hypothesis has failed to explain the capillary–ISF transfer in most parts of the body.

A concept based on a new hydrodynamic phenomenon is proposed for the capillary–ISF circulation hypothesis. It explains this vital circulation in every organ and tissue under both physiological and pathological conditions. An autonomous dynamic magnetic field-like G–C circulation occurs between fluid in the G tube’s lumen and a surrounding fluid compartment C. Based on results of studies on a circulatory model incorporating the G–C apparatus, factors which initiate, regulate and affect the G–C circulation, its physiological and haemodynamic relevance and its clinical importance to the pathogenesis of oedema, shock and the MVOD/F syndrome are discussed.

Acknowledgement

I thank Professors GD Chisholm, Eric Neil, Cyril Keele, Dr Antony Winward, Mr BJ Stoodley and Mr PL Brooks for helpful comments and encouragement, Mr Peter Holder, Designer Engineer, Eastbourne, for making the G–C model and board used for quantitative measurements and Mr and Mrs Freda and Robert Prentice for permitting the generous use of their premises at 70, Glendale Avenue, Eastbourne, BN21 UN, during the G tube studies.

Conflict of interest

None declare

References

1. Starling EH (1886) Factors involved in the causation of dropsy. Lancet d ii: 1266-1270, 1330-1334 and 1406-1410.
2. Folkow B, Neil E (1971) Circulation Oxford University Press: 1-125.
3. Rhodin JA (1967) The ultrastructure of mammalian arterioles and precapillary sphincters. J Ultrastruct Res 18: 181-223. [Crossref]
4. Karnovsky MJ (1967) The ultrastructural basis of capillary permeability studied with peroxidase as a tracer. J Cell Biol 35: 213-236. [Crossref]
5. HENDRY EB (1962) The osmotic pressure and chemical composition of human body fluids. Clin Chem 8: 246-265. [Crossref]
6. Guyton AC, Coleman TG (1968) Regulation on interstitial fluid volume and pressure. Ann N Y Acad Sci 150: 537-547. [Crossref]
7. Calnan JS, Pflug JJ, Chisholm GD, Taylor LM (1972) Pathophysiology of tissue fluid. Proc R Soc Med 65: 715-719. [Crossref]
8. Keele CA, Neil E, Joels N (1982) Sampson Wright Applied Physiology. 13th Ed. Oxford University Press, Oxford.
9. Renkin EM (1986) Some consequences of capillary permeability to macromolecules: Starling’s hypothesis reconsidered. Am J Physiol 250: 19: H706–H710. [Crossref]
10. Ghanem AN (2001) Magnetic field-like fluid circulation of a porous orifice tube and its relevance to the capillary-interstitial fluid circulation: preliminary report. Med Hypotheses 56: 325-334 [Crossref]
11. Ghanem AN (1988) The Transurethral Prostatectomy (TURP) Syndrome: An Investigation of the Osmotic and Metabolic Sequelae of Volumetric Overload. MD Thesis. Institute of Urology and Nephrology, Mansoura University, Mansoura, Egypt.
12. Ghanem AN, Ward JP (1990) Osmotic and metabolic sequelae of volumetric overload in relation to the TUR syndrome. Br J Urol 66: 71-78. [Crossref]
13. Landis EM (1929) Micro-injection studies of capillary blood pressure in human skin. Heart 31: 209-228.
14. Pappenheimer JR, Soto-Rivera (1948) Effective osmotic pressure of plasma proteins and other quantities associated with capillary circulation in the hind limbs of cats and dogs. Am J Physiol 152: 471-491. [Crossref]
15. Mellander S (1960) Comparative studies on the adrenergic neurohormonal control of resistance and capacitance blood vessels in the cat. Acta Physiol Scand 50: 176: 1-86.
16. Mattfeldt T, Mall G (1984) Estimation of length and surface of anisotropic capillaries. J Microsc 135: 181-190. [Crossref]
17. Guyton AC (1986) Textbook of Medical Physiology. An HBJ International Seventh Edn. WB Saunders Company. Philadelphia London 19: 221.
18. Ghanem AN, Ghanem SA (2016) Volumetric Overload Shocks: Why Is Starling’s Law for Capillary Interstitial Fluid Transfer Wrong? The Hydrodynamics of a Porous Orifice Tube as Alternative. Surgical Science 7: 245-249.
19. Pindoria Nisha, Ghanem Salma A, Ghanem Khalid A, Ghanem Ahmed N (2017) Volumetric overload shocks in the pathoetiology of the transurethral resection prostatectomy syndrome and acute dilution hyponatraemia. Integr Mol Med. 4: 1-5.
20. Ghanem Khaled A. and Ghanem Ahmed N (2017) Volumetric overload shocks in the patho-etiology of the transurethral resection prostatectomy syndrome and acute dilution hyponatraemia: The clinical evidence based on 23 case series. Basic Research Journal of Medicine and Clinical Sciences 6.