Take a look at the Recent articles

Abstract

Surgical correction with corpectomy and subsequent fusion of neighboring levels is a commonly practiced treatment for thoracolumbar burst fractures. Different fixation constructs are currently implemented to fuse the injured level. However, little is known about the implications of such constructs on the biomechanics of the adjacent spine segments. The objective of this study is to compare the biomechanical alterations at the adjacent segments due to implanted construct.

A 3D nonlinear finite element model of the thoracolumbar spine (from T12 to S1) was used for assessing changes in the biomechanics of the adjacent spine segments. First, the vertebral body and the adjacent discs of the operated level (L1) were completely excised leaving only the posterior elements. Next, four constructs were implanted at the thoracolumbar junction (T12-L2): (1) 2RPC which includes two posterior rods, six pedicle screws, an expandable cage, and a transverse plate; (2) 1RPC which includes the same instrumentation of 2RPC with the exclusion of the posterior rod contralateral to the transverse plate; (3) 2RC which includes posterior rods, pedicle screws, and an expandable cage; (4) PC which includes the expandable cage and the transverse plate. Models were validated by comparing their predicted range of motion (ROM) to in vitro biomechanical tests. Subsequently, the stresses generated at all the adjacent levels (L2-L3, L3-L4, L4-L5, and L5-S1) were measured and compared.

The results showed that the constructs including pedicle screws (2RPC, 1RPC, 2RC) yielded similar biomechanical performance being the stiffest. Moreover, the same constructs demonstrated comparable stress levels at the adjacent segments, generating 50% higher than that produced from the PC construct. Elevated mechanical stress is believed to be a cause of disc degeneration. Accordingly, the PC construct, although less reliable in stabilizing the injured segment, represented the most conservative approach for preventing potential development of adjacent disc degeneration.

Key words

 adjacent segment degeneration disease, intervertebral disc, low back pain, burst fracture, spine fusion, biomechanics, finite element analysis, corpectomy

Introduction

The majority of traumatic spinal fractures are found at the thoracolumbar region and nearly 10-20% of these injuries are burst fracture (BF) [1,2]. Surgical correction with corpectomy and subsequent fusion of neighboring levels is a commonly practiced treatment for BF injury [3]. The goal of the surgery is to correct sagittal deformity, stabilize the spine column, decompress neural elements, and restore vertebral body height [4-7]. The optimal surgical approach for treatment of BF is controversial [8,9]. It can be performed through anterior, posterior, or combined anterior-posterior approach [7,10,11]. Short-segment posterior fixation, by solely fusing the immediate superior and inferior levels of the injured level, is preferred by many surgeons to preserve natural spine mobility and to reduce surgical insult [12,13]. Such procedure can be attained through various types of constructs which may employ pedicle screws, posterior rods, expandable cages, and transverse plate [14-17]. In particular, pedicle screws together with the posterior rods had become the gold standard in fixing spine levels due to its high ability in retaining bony purchase until the fusion mass stabilizes [18]. Also, expandable cage is considered among the best implants that maintain anterior column reconstruction [17]. Moreover, lateral fixation by transverse plate has been proposed in anterolateral approach to avoid second posterior surgery [16]. Each of these implants has different mechanical properties and provides dissimilar stiffness to the fixed junction. Accordingly, the postoperative mechanical behavior of the spine is supposed to vary based on the adopted construct.

Many studies reported that the excessive stiffness, produced from fixing spinal levels, causes greater motion on the adjacent intervertebral disc (IVD) to compensate the range of motion lost by fusion [19-21]. Such alterations may potentially lead to adjacent segment disc degeneration (ASDD) [22]. The ASDD is a pathological condition associated to chronic low back pain, a disease of epidemic proportions [20-22]. To date, no study investigated the implications of short-segment fixation procedures used in treatment of BF on the health of the adjacent segments. Accordingly, the objective of this study was to quantify the biomechanical alterations at the adjacent lumbar spine segments after implanting different short-segment fixation constructs aimed at treatment of thoracolumbar BF. Since the higher is the stress on the adjacent discs the higher is the risk of disc degeneration [23], this study specifically quantified the changes of stress at adjacent segment after adding pedicle screws and transverse plate to the fixation construct. This was attained by developing finite element (FE) models of the thoracolumbar spine that described four different fixation constructs.

Methods

First, four 3D nonlinear FE models from T12 to L2, representing different fixation constructs, were developed. Next, the models were validated by comparing their prediction of ROM with experimental data [23]. Then, each construct was integrated with a lumbar spine to constitute a thoracolumbar spine model (from T12 to S1) that was tested by simulating flexion-extension moment. Finally, the generated stresses at the adjacent IVDs were computed and compared among the four constructs. Non-commercial software FEBio (FEBio 2.2.0, Musculoskeletal Research Laboratory, University of Utah, Salt Lake City, UT) was employed to solve the FE models [24,25].

Computational model of the constructs: Four FE models of the thoracolumbar junction were developed from a CT scan of a healthy male subject via commercially available image processing software (Mimics Research 17.0×64; Materialise, Louvain, Belgium). The models were used to describe the mechanical behavior of four different fixation constructs used for treatment of BF. Before implanting the constructs, a complete corpectomy at L1 level was performed by subtracting both the L1 vertebral body and the adjacent IVDs. In all investigated constructs, an expandable cage was placed between T12 and L2 to restore the height of the anterior column. The instrumentation combination of the investigated constructs were as follows: (1) 2RPC which includes two titanium posterior rods of 5.5 mm diameter , six pedicle screws of 6 mm diameter, an expandable cage, and a transverse plate laterally fixed (Figure 1a); (2) 1RPC which includes the same instrumentation of 2RPC with the exclusion of the posterior rod contralateral to the transverse plate (Figure 1b); (3) 2RC which includes posterior rods, pedicle screws, and expandable cage (Figure 1c); (4) PC which includes the expandable cage and the transverse plate (Figure 1d). The instrumentation utilized in the constructs was assumed to have material property of titanium with an elastic modulus of 110 GPa and Poisson’s ratio of 0.3 [26]. Sliding interfaces were defined between the expandable cage and the surfaces of the vertebral bodies of T12 and L2, with friction coefficient of 0.8 to prevent the cage from slipping [27]. The pedicle screws were placed posteriorly and connected with posterior rods by a tied contact. The transverse plate was connected via four lateral screws to T12 and L2 vertebral bodies, and a sliding contact with 0.1 friction coefficients was assumed between the plate and the vertebral body [28]. The four construct models were validated by comparing their predictions of ROM during flexion-extension with an in vitro experimental data [23].

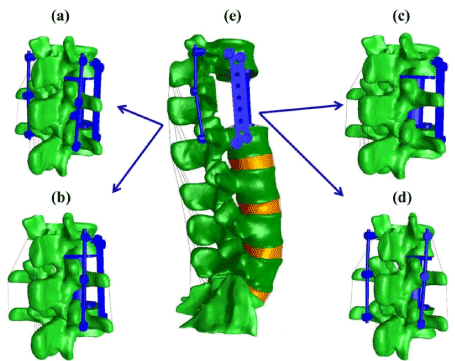
Figure 1. Thoracolumbar spine FE model with different fixation constructs. (a) 2RPC construct; (b) 1RPC construct; (c) PC construct; (d) 2RC construct; (e) constructs integrated with the intact lumbar spine. Each construct will replace the intact spine levels (T12-L2) to generate the studied FE models

Computational model of the thoracolumbar spine: After validating the models of the four T12-L2 constructs, four vertebrae (from L3 to S1) with its associated intervertebral discs (IVDs), facet joints, and major ligaments were added to each model (Figure 1e). The geometry of the vertebral bodies, comprising cortical and cancellous bone, was reconstructed from the CT scan of the same healthy spine. The IVDs were defined as two distinct anatomic regions: the annulus fibrosis (AF) and nucleus pulposus (NP). Both regions were assumed as a biphasic material constituted of a solid phase embedded in a fluid phase [29]. In particular, the solid phase of AF was modeled as a hyperelastic material reinforced with fibers: the ground substance of AF was as a Mooney-Rivlin material [30], while the collagen fibers were assumed as tension-only elements [31] and arranged in four concentric layers enfolding the NP with alternating ±30° orientation [32]. The solid phase of NP was modeled as isotropic elastic material [33]. Water volumetric fractions and hydraulic permeability for both AF and NP were those reported in the literature [34,35]. A cartilage layer of 0.5 mm was built on the surface of the facet joints and its material properties was assumed to be isotropic linear elastic. A gap of 0.4 mm was specified between cartilage layers with a sliding interface between the superior and inferior cartilage [36]. All seven spinal ligaments, including supraspinous ligament, interspinous ligament, transverse ligament, capsular ligament, flavum ligament, posterior longitudinal ligament, and anterior longitudinal ligament were modeled as linear elastic tension-only spring elements [37]. The material properties for all model constituents were taken from the literature, and are reported in Table 1. Four-node solid elements were used for discretizing the cortical and cancellous bones, the IVDs, and the facet joints. On average, each vertebra, IVD, and facet joint consisted of 65,000, 3500, and 1000 elements, respectively.

Table 1. Material properties of the different tissues used in the finite element model

Material	Property	Value	Reference
Cortical bone	Moduli in MPa	E=12,000	[46]
	Poisson’s ratio	n=0.3
Cancellous bone	Moduli in MPa	E=100
	Poisson’s ratio	n=0.2
Annulus fibrosus	Ground sub. Mooney-Rivlin coeff.	c1=0.18; c2=0.045	[30]
	Collagen fibers (tension-only)	Stress–strain curve	[31]
	Hydraulic permeability	0.00021 mm4N-1s-1	[35]
	Volumetric fluid fraction	0.75	[34]
Nucleus pulposus	Ground sub. isotropic elastic moduli	E=0.2 MPa	[33]
	Ground sub. poisson’s ratio	n=0.499
	Hydraulic permeability	0.00067 mm4N-1s-1	[47]
	Volumetric fluid fraction	0.86	[34]
Cartilage	Moduli in MPa	E=35	[36]
	Poisson’s ratio	n=0.4
Ligaments	Stiffness (tension-only)	Linear elastic	[37]

Loading and boundary conditions: Testing conditions were similar to those reported in [23]. Specifically, the four FE models obtained by integrating the four different constructs with the lumbar spine were subjected to pure flexion-extension moment of 5 Nm with a frequency of 0.25 Hz. The models were constrained by fixing the S1 in all directions. The flexibility testing method was adopted as a protocol for loading the spine. Such approach guarantees that the pure moment is equally applied to all the segments as the spine deforms [38]. The post-operative alterations of von-misses stress at all adjacent segments (i.e., L2-L3, L3-L4, L4-L5, and L5-S1) was calculated and compared.

Results

For all investigated constructs, the predicted ROM during flexion-extension was in agreement with the in vitro experimental data (Figure 2). The smallest range of motion corresponded to the 2RPC construct, while the largest ones were found in the PC constructs.

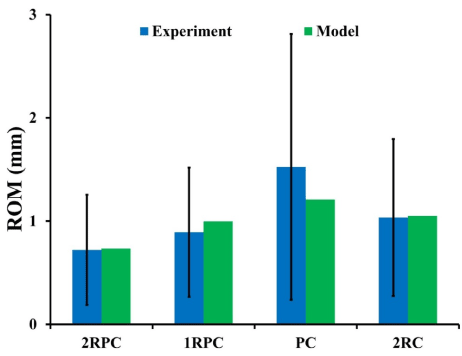
Figure 2. FE constructs models’ prediction of ROM compared to experimental data during flexion-extension (bars represent +/- σ)

On the adjacent spine levels, all the constructs that comprised pedicle screws (i.e. 2RPC, 1RPC, 2RC) produced comparable ROM, which was always higher than that produced from the PC construct. Specifically, during flexion, the maximum ROM was found at L4-L5 level (~1.4°), while, during extension, the maximum ROM was observed at L3-L4 and L4-L5 levels reaching up to 2° (Figure 3). Consistently, the same constructs that comprised pedicle screws generated analogous magnitude of stresses which was also higher than that produced form the PC construct. In particular, in flexion, the highest stresses in AF and NP were found at L5-S1 level reaching up to 5 MPa and 0.37 MPa, respectively (Figure 4). Similarly, during extension, the maximum stresses in AF and NP were found at L5-S1 level reaching up to 4 MPa and 0.56 MPa respectively (Figure 5). The only exception was at L2-L3 level during flexion, where the stresses produced by 2RC in AF was 30% less than that attained with 1RPC or 2RPC. Stress levels produced by the PC construct in all the investigated cases were approximately 50% smaller than those corresponding to the other constructs.

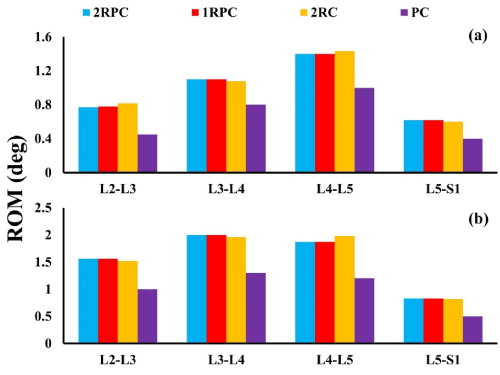
Figure 3. ROM in degrees at the adjacent IVDS for all investigated constructs: (a) during flexion; (b) during extension

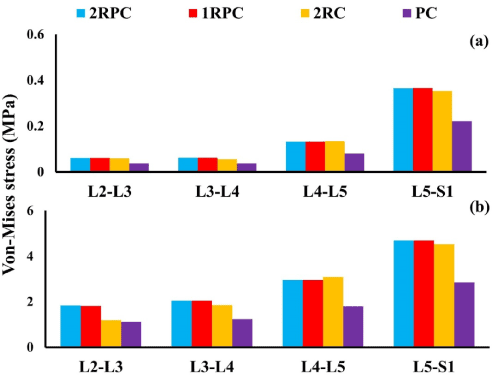
Figure 4. Von-Misses stress at the adjacent IVDs during flexion for all investigated constructs: (a) NP; (b) AF

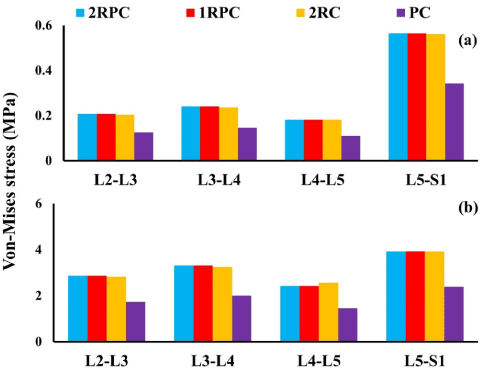
Figure 5: Von-Misses stress at the adjacent IVDs during extension for all investigated constructs: (a) NP; (b) AF

Discussion

Spinal fixation is believed to be a possible cause for degeneration of the adjacent segments [39,40]. In a recent long follow-up study (~13 years), Mannion and co-workers found that spinal fusion is associated with signs of disc degeneration at the adjacent segments [41]. Moreover, biomechanical experiments showed that the mobility and stresses experienced by a spinal segment increased when the neighboring segments were fused [20,21]. Hence, monitoring the stresses generated at the adjacent segment due to implanted construct provides an indication on the potential risks of degeneration at the adjacent IVD.

In this study, four different constructs that are commonly used in short-segment fixation for treatment of BF were compared to investigate their implication on the biomechanics of the adjacent lumbar segments. This was done by developing four thoracolumbar FE models, each of them comprising an expandable cage and different combination of pedicle screws and transvers plate. A flexion-extension moment was simulated and the generated stresses at all adjacent segments were computed. The results showed that the three constructs that comprised posterior pedicle screws (2RPC, 1RPC, and 2RC) yielded similar rigidity and were the stiffest. Specifically, the 2RPC construct produced the lowest ROM (0.73 mm), while the PC construct produced the highest (1.2 mm) (Figure 2). Moreover, the stress levels on the adjacent lumbar segments varied according to the adopted construct. In particular, for 2RPC, 1RPC, and 2RC constructs, stresses at all adjacent levels were approximately 50% higher than that produced by the PC construct (Figures 4 and 5). It has been suggested that mechanical loads and stresses alter the structure, material, and failure properties of the disc, eventually leading to IVD degeneration [42]. Also, the higher stiffness induced by constructs that comprised pedicle screws might be attributed to the major role that pedicle screws are playing in constraining the fused junction during flexion-extension loading conditions [18].

Some limitations in this study must be noted. The thoracolumbar spine was reconstructed from a CT scan of only one subject. The geometry of the vertebral body may influence the mechanical behavior of the spine [43]. Hence, in the future, it will be important to extend the analysis by including CT scans of several subjects to broaden the validity of the results of this study. Also, muscle forces were not included in the models. Spinal muscles contribute to the stability of the spine [44]. However, all the constructs investigated underwent the same testing protocol. Thus, minor relative changes should be expected in the biomechanical performance of the four constructs. Moreover, only flexion and extension loading conditions were simulated. This was due to the lack of experimental data for the other loading conditions that is required for model validation. In the future, other loading conditions will be considered to broaden the conclusion of this study. Finally, the flexibility test method was used instead of the hybrid test method, which is considered the most appropriate protocol for investigating the adjacent segments due to fusion [45]. However, in this analysis, the objective was to compare the implications produced from each construct not to quantify how much it will change from the intact spine. Also, no data are available in the literature for the total ROM for the thoracolumbar spine (T12-S1) when pure moment is applied, as is required for conducting the hybrid protocol.

Conclusion

In conclusion, this study provides new insights on the implications of choice of fixation construct for treatment of thoracolumbar BF on the biomechanics of the adjacent lumbar segments. The results suggest that the PC construct, although less stable in fixing the injured segment, yields the least amount of stress on lumbar adjacent segments. Since high mechanical stresses are believed to be a potential cause of disc degeneration, the PC construct represents the most conservative approach for preventing the development of ASDD.

References

1. Esses SI, Botsford DJ, Kostuik JP (1990) Evaluation of surgical treatment for burst fractures. Spine (Phila Pa 1976) 15: 667-673. [Crossref] 
2. Dai LY, Jiang SD, Wang XY, Jiang LS (2007) A review of the management of thoracolumbar burst fractures. Surg Neurol 67: 221-231. [Crossref] 
3. Bradford DS, Mcbride GG (1987) Surgical management of thoracolumbar spine fractures with incomplete neurologic deficits. Clin Orthop Relat Res 218: 201-216. [Crossref] 
4. Jacobs RR, Casey MP (1984) Surgical Management of Thoracolumbar Spinal Injuries General Principles and Controversial Considerations. Clin Orthop Relat Res 189: 22-35.
5. Shono Y, McAfee PC, Cunningham BW (1994) Experimental Study of Thoracolumbar Burst Fractures: A Radiographic and Biomechanical Analysis of Anterior and Posterior Instrumentation Systems. Spine 19: 1711-1722.
6. Hitchon PW, Torner JC, Haddad SF, Follett KA (1998) Management options in thoracolumbar burst fractures. Surg Neurol 49: 619-626. [Crossref] 
7. Been H, Bouma G (1999) Comparison of two types of surgery for thoraco-lumbar burst fractures: combined anterior and posterior stabilisation vs. posterior instrumentation only. Acta Neurochirurgica 141: 349-357.
8. Pneumaticos SG, Triantafyllopoulos GK, Giannoudis PV (2013) Advances made in the treatment of thoracolumbar fractures: current trends and future directions. Injury 44: 703-712.
9. Wood KB, Li W, Lebl DR, Ploumis A (2014) Management of thoracolumbar spine fractures. Spine J 14: 145-164. [Crossref] 
10. Wood K, Bohn D, Mehbod A (2005) Anterior versus posterior treatment of stable thoracolumbar burst fractures without neurologic deficit: a prospective, randomized study. J Spinal Disord Tech 18: S15-S23. [Crossref]
11. Scheer JK, Bakhsheshian J, Fakurnejad S, Oh T, Dahdaleh NS, et al. (2015) Evidence-Based Medicine of Traumatic Thoracolumbar Burst Fractures: A Systematic Review of Operative Management across 20 Years. Global Spine J 5: 73-82. [Crossref]
12. Kramer DL, Rodgers W, Mansfield FL (1995) Transpedicular instrumentation and short-segment fusion of thoracolumbar fractures: a prospective study using a single instrumentation system. J Orthop Trauma 9: 499-506. [Crossref]
2021 Copyright OAT. All rights reserv
13. Stovall DO Jr, Goodrich A, MacDonald A, Blom P (1996) Pedicle screw instrumentation for unstable thoracolumbar fractures. J South Orthop Assoc 5: 165-173.
14. Sasani M, Özer AF (2009) Single-stage posterior corpectomy and expandable cage placement for treatment of thoracic or lumbar burst fractures. Spine 34: E33-E40.
15. Papanastassiou ID, Gerochristou M, Aghayev K, Vrionis FD (2013) Defining the indications, types and biomaterials of corpectomy cages in the thoracolumbar spine. Expert Review of Medical Devices 10: 269-279.
16. Kim SM, Lim TJ, Paterno J, Park J, Kim DH (2005) Biomechanical comparison: stability of lateral-approach anterior lumbar interbody fusion and lateral fixation compared with anterior-approach anterior lumbar interbody fusion and posterior fixation in the lower lumbar spine. J Neurosurg Spine 2: 62-68. [Crossref]
17. Eleraky M, Papanastassiou I, Tran ND, Dakwar E, Vrionis FD (2011) Comparison of polymethylmethacrylate versus expandable cage in anterior vertebral column reconstruction after posterior extracavitary corpectomy in lumbar and thoraco-lumbar metastatic spine tumors. Eur Spine J 20: 1363-1370.
18. Hamill CL, Lenke LG, Bridwell KH, Chapman MP, Blanke K, et al. (1996) The use of pedicle screw fixation to improve correction in the lumbar spine of patients with idiopathic scoliosis: Is it warranted? Spine 21: 1241-1249. [Crossref]
19. Lee MJ, Dettori JR, Standaert CJ, Brodt ED, Chapman JR (2012) The natural history of degeneration of the lumbar and cervical spines: a systematic review. Spine (Phila Pa 1976) 37: S18-S30. [Crossref] 
20. Hilibrand AS, Robbins M (2004) Adjacent segment degeneration and adjacent segment disease: the consequences of spinal fusion? Spine J 4: 190S-194S. [Crossref] 
21. Park P, Garton HJ, Gala VC, Hoff JT, McGillicuddy JE (2004) Adjacent segment disease after lumbar or lumbosacral fusion: review of the literature. Spine (Phila Pa 1976) 29: 1938-1944. [Crossref]
22. Battié MC, Lazáry A, Fairbank J, Eisenstein S, Heywood C, et al. (2014) Disc degeneration-related clinical phenotypes. Eur Spine J 23: 305-314.
23. Gjolaj JP, Hirsch BP, Latta L, Eismont FJ (2016) Biomechanical Evaluation of Lateral-Access Anterior Instrumentation for Thoracolumbar Instability. The Spine Journal 16: S256.
24. Ateshian GA, Maas S, Weiss JA (2012) Solute transport across a contact interface in deformable porous media. J Biomech 45: 1023-1027. [Crossref] 
25. Maas SA, Ellis BJ, Ateshian GA, Weiss JA (2012) FEBio: finite elements for biomechanics. J Biomech Eng 134: 011005. [Crossref] 
26. Kim Y (2007) Finite element analysis of anterior lumbar interbody fusion: threaded cylindrical cage and pedicle screw fixation. Spine 32: 2558-2568.
27. Polikeit A, Ferguson SJ, Nolte LP, Orr TE (2003) Factors influencing stresses in the lumbar spine after the insertion of intervertebral cages: finite element analysis. Eur Spine J 12: 413-420.
28. Park WM, Park YS, Kim K, Kim YH (2009) Biomechanical comparison of instrumentation techniques in treatment of thoracolumbar burst fractures: a finite element analysis. J Orthop Sci 14: 443-449.
29. Travascio F, Asfour S, Gjolaj J, Latta LL, Elmasry S (2015) Implications of Decompressive Surgical Procedures for Lumbar Spine Stenosis on the Biomechanics of the Adjacent Segment: A Finite Element Analysis. J Spine 4: 220.
30. Schmidt H, Heuer F, Simon U, Kettler A, Rohlmann A, et al. (2006) Application of a new calibration method for a three-dimensional finite element model of a human lumbar annulus fibrosus. Clin Biomech (Bristol, Avon) 21: 337-344. [Crossref]
31. Shirazi-Adl A, Ahmed AM, Shrivastava SC (1986) Mechanical response of a lumbar motion segment in axial torque alone and combined with compression. Spine 11: 914-927. [Crossref]
32. Zander T, Rohlmann A, Calisse J, Bergmann G (2001) Estimation of muscle forces in the lumbar spine during upper-body inclination. Clin Biomech (Bristol, Avon) 16 Suppl 1: S73-S80. [Crossref] 
33. Natarajan RN, Andersson GB (1999) The influence of lumbar disc height and cross-sectional area on the mechanical response of the disc to physiologic loading. Spine (Phila Pa 1976) 24: 1873-1881. [Crossref] 
34. Antoniou J, Steffen T, Nelson F, Winterbottom N, Hollander AP, et al. (1996) The human lumbar intervertebral disc: evidence for changes in the biosynthesis and denaturation of the extracellular matrix with growth, maturation, ageing, and degeneration. J Clin Invest 98: 996. [Crossref] 
35. Iatridis JC, Setton LA, Foster RJ, Rawlins BA, Weidenbaum M, et al. (1998) Degeneration affects the anisotropic and nonlinear behaviors of human anulus fibrosus in compression. J Biomech 31: 535-544. [Crossref] 
36. Schmidt H, Galbusera F, Rohlmann A, Zander T, Wilke HJ (2012) Effect of multilevel lumbar disc arthroplasty on spine kinematics and facet joint loads in flexion and extension: a finite element analysis. Eur Spine J 21: 663-674. [Crossref] 
37. Pintar FA Yoganandan N, Myers T, Elhagediab A, Sances A Jr (1992) Biomechanical properties of human lumbar spine ligaments. J Biomech 25: 1351-1356. [Crossref] 
38. Panjabi M (1988) Biomechanical evaluation of spinal fixation devices: I. A conceptual framework. Spine (Phila Pa 1976) 13: 1129-1134. [Crossref]
39. Goto K, Tajima N, Chosa E, Totoribe K, Kubo S, et al. (2003) Effects of lumbar spinal fusion on the other lumbar intervertebral levels (three-dimensional finite element analysis). J Orthop Sci 8: 577-584. [Crossref]
40. Rahm MD, Hall BB (1996) Adjacent-segment degeneration after lumbar fusion with instrumentation: a retrospective study. J spinal disord 9: 392-400.
41. Mannion AF, Leivseth G, Brox JI, Fritzell P, Hägg O, et al. (2014) ISSLS Prize Winner: Long-Term Follow-up Suggests Spinal Fusion Is Associated with Increased Adjacent Segment Disc Degeneration But Without Influence on Clinical Outcome: Results of a Combined Follow-up From 4 Randomized Controlled Trials. Spine 39: 1373-1383. [Crossref]
42. Stokes IA, Iatridis JC (2004) Mechanical conditions that accelerate intervertebral disc degeneration: overload versus immobilization. Spine 29: 2724-2732. [Crossref]
43. Panjabi MM, Goel V, Oxland T, Takata K, Duranceau J, et al. (1992) Human lumbar vertebrae. Quantitative three-dimensional anatomy. Spine (Phila Pa 1976) 17: 299-306. [Crossref] 
44. Wilke HJ, Wolf S, Claes LE, Arand M, Wiesend A (1995) Stability increase of the lumbar spine with different muscle groups. A biomechanical in vitro study. Spine (Phila Pa 1976) 20: 192-198. [Crossref] 
45. Panjabi MM (2007) Hybrid multidirectional test method to evaluate spinal adjacent-level effects. Clinical Biomechanics 22: 257-265.
46. Cowin SC (2001) Bone mechanics handbook.
47. Périé D, Korda D, Iatridis JC (2005) Confined compression experiments on bovine nucleus pulposus and annulus fibrosus: sensitivity of the experiment in the determination of compressive modulus and hydraulic permeability. J Biomech 38: 2164-2171.