Abstract
Making causal inference is conceptually straightforward in the setting of a randomized intervention, such as a clinical trial. However, in observational studies, which represent the majority of most large-scale epidemiologic studies, causal inference is complicated by confounding and lack of clear directionality underlying an observed association. In most large scale biomedical applications, causal inference is embodied in Directed Acyclic Graphs (DAG), which is an illustration of causal relationships (i.e. arrows) among the variables (i.e. nodes). A key concept for making causal inference in the context of observational studies is the assignment mechanism, whereby some individuals are treated and some are not. This perspective provides a structure for thinking about causal networks in the context of the assignment mechanism (AM). Estimation of effect sizes of the observed directed relationships is presented and discussed.
Introduction
Inferring cause-effect relationships among variables is of primary importance in many sciences and is growing in importance as a result of very large datasets in health, and genomics. There are several statistical frameworks underlying causal inference, such as those of Rubin’s potential outcome framework [1,2], Pearl’s structural equation modeling framework [3], and Dawid’s regime indicator framework [4], that have been established for making causal inference. These frameworks are hardly known to most biomedical researchers or biostatisticians who could by applying them to address real world problems. Large segments of the statistical community and decision makers find it hard to benefit from causal analyses. The main reason, we believe, is not a philosophical barrier about data analysis establishing causality, but rather lack of familiarity with the vocabulary and methods in the field. Undertaking statistical causal inference requires systematic extensions to the standard language of statistics, and this perspective provides a step toward this end.
Among available statistical causal inference frameworks, Pearl’s causal network, which are compatible with structural equation models (SEM) [3], can be seen as a pragmatic approach to solving real world problems, especially in the age of large data sets. [5] has critiqued Pearl’s framework and suggests that it requires additional explicit, methodological and philosophical justification. The concept of the assignment mechanism developed by Rubin (2005) describes the circumstances by which some individuals are exposed to a treatment of interest and some are not. In this perspective, we first connect causal networks to the concept of the assignment mechanism (AM). Then, we formalize the causal network parameterization using the AM notation. After discussing the concept and notations of causal networks and the AM, we estimate the direct and total effects.
Overview of the Assignment Mechanism
The questions that motivate most studies in the health, economics, social and behavioral sciences are causal relationships and not only associations, such as the efficacy of a given drug in a given population. The classical approach for determining such relationships uses randomized experiments where single or a few variables are intervened on. Such intervention experiments, however, are expensive, unethical or even infeasible. Hence, it is desirable to infer causal effects from so-called observational data obtained by observing a system without subjecting it to interventions. Then, to estimate the effect of a treatment on a response, we need to know how different values of the treatment are assigned. The circumstances by which some individuals are exposed to a treatment of interest and some are not is called the assignment mechanism (AM).
To achieve causal inference, the important data elements include not only the value of the observations but also the reason why one of the possible exposures or treatments has been realized and not others. The notation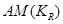 
is introduced as the third element (in addition to treatment and response value) and is called the causal element [6]. The practitioners need to understand the underlying mechanisms by which some individuals have a certain exposure level and some do not. The knowledge related to response is represented by 
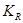and is required to identify the AM. In a randomized clinical trial the AM is straight forward (i.e. the treatment assignment mechanism is unrelated to response) and presumably under the control of the investigators. In an observational study, many factors (covariates) may influence the AM but only some of them are related to response. Variables that influence both the outcome and the AM are termed confounders [7]. The aim of considering the AM is to identify individuals with similar covariate distributions as if there were a randomization. In an epidemiologic study, this is equivalent to matching [8]. In a data analysis setting, this is equivalent to SEM [3], where the AM is understood and modeled. Formalizing the AM in the context of causal networks compatible with the SEM is more practical in the age of big data. Therefore, in this study, we formalize the AM within the context of statistical causal networks.
Causal networks are illustrations of the AM, the data generating process underlying the study observations, and provide a pragmatic approach to distinguish confounders of the AM from among the covariates, and allows one to analyze observational data as if an intervention was carried out. To the analyst, causal graphs are illustrations of the data generating process [3] (i.e. assignment mechanism [2] that underlie the observations. It is important to understand and take into account that the model in a causal setting is conditioned explicitly or implicitly on illumination of assignment mechanism.
Assume the assignment mechanism over p variables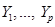 
is formalized by a network, here a Directed Acyclic Graph (DAG). The distribution P over these variables is:
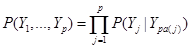, (1)
where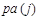
denotes the set of predecessors of node j and are directly connected to j in the network, called parents of node j. For
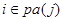, there is 
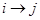in the DAG or 
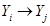. Note that the formula in (1) represents the Markov properties over these set of variables compatible with the underlying DAG, an illustration of the assignment mechanism that governs over this set of variables. This is a strong assumption in application of DAGs and can be represented in (1) as
.
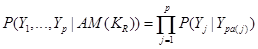By conditioning factorized distributions on the causal element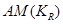
, we explicitly represent that the AM is taken into account and the work can, therefore, be considered to be within a causal setting.
Assume the AM over four variables X, Y, Z and H is illustrated in Figure 1. The variable of interest is H, and we are typically investigating the influence of the other variables on H. To factorize the joint distribution over these 4 variables, we first identify potential confounders. (Figure 1)
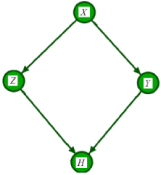
Figure 1: The illustration of the assignment mechanism of variable H formalized as a DAG over four variables.
Variables X, Y, and Z are all called covariates. However, the effect of X reaches to H only through Z and Y. Therefore, X is not a confounder of the value of H. The set of confounders for variable H is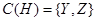
. The interested reader is referred to the backdoor criterion in [3] for further information. The joint probability over these variables are then factorized as
.
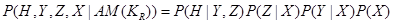Without conditioning on the causal element,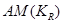
, such a unique factorization is not possible [9,10].
Formally Representation of Causal Networks
Assume a DAG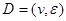
, where 
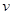is a set of nodes with p elements, corresponds a set of p random variables with joint Gaussian distribution and 
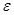is a set of edges which connect the nodes and represent the conditional dependencies between two corresponding variables. The existence of a directed edge between two nodes shows the direction of effect (the flow of information) between the correspondent variables. The concept of a DAG
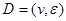depends on the nodes in 
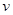and edges in 
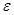and any inference depends on the set (
,
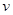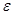). Assume 
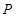is a joint probability distribution over variables 
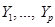corresponding with nodes in DAG
. 
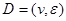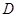and P must satisfy the Markov condition, the strong assumption in causal inference by networks. This means variables are related with the causal network DAG
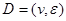. Furthermore, we assume these variables have a joint normal distribution which satisfies the Markov property with respect to the DAG D and all marginal and conditional independencies can be directly obtained from the graph D: every variable 
, 
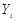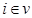is independent of any subset of its predecessors conditioned on the set of its direct or immediate causes of 
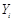, corresponding with parents of i,
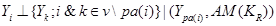
where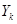 
occurs before 
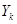and parental set
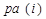denotes the set of parents of node i relatives to AM formalized by
.
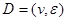In SEM and under the assumption of a Gaussian distribution, we can write
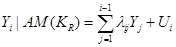, (2)
where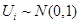 
and is independent of the 
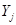s in the right side of the model. 
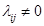is equivalent with an edge 
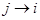in DAG D which is due to compatibility of SEM and AM formalized as the DAG D. Therefore, the coefficients can be interpreted as statistical causal effects. SEM is a deterministic form of probability models or conditional dependencies, where all uncertainties are confined in the variable U.
Given a causal network structure, the goal in this section is to infer edge weights for the directed arrows in the network (the strength of each causal relationship). We first define direct, indirect, and total effects, and then represent the computation by the backdoor criterion [3]. A direct effect is the effect through an immediate path, with no other intervening variables/mediators. Total effect is defined as an effect with or without intermediation of other variables. In Figure 2, the effect of X on Z through path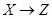 
is the direct effect and through path 
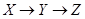is called the indirect effect. The effect X on Z through these two paths is called the total effect. The effect of Y on Z in Figure 2 is only through the direct path
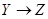. Therefore, the direct and total effects of Y on Z are the same. To obtain this effect, X, in the back-door path
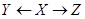is called a confounder. In other words, X confounds the assigning mechanism Y on Z since X influences both Y and Z. Recall that the causal network structure in Figure 2 is an illustration of the assignment mechanism over these three variables and all discussions and equations for the effect measurement is given the assignment mechanism illumination.
(Figure 2) In this structure, variable X has direct effect and indirect effect on variable Z. The latter is via variable Y. Variable Z does not have any effect on variables X and Y. The effect of Y on Z is confounded by X.
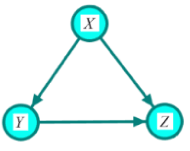
Figure 2: Illumination of the assignment mechanism for the variable of interest Z.
To estimate the direct effect of Y on Z, we need to consider the causal element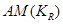 
embodied in the DAG in Figure 2, which illustrates the assignment mechanism behind the observed variables Y and Z. By taking the causal element into account, we see that variation in X causes variation in both Y and Z. To find the effect of Y (and not X) on Z, we first adjust for the effect of X on Y by
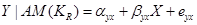, (3)
and then find the effect of variations in Y on Z by
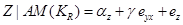(4)
Equation (4) represents the degree to which variable Y is responsible for the variation in Z, regardless of the values of the variable X. Therefore, the coefficient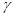 
is interpreted as the statistical causal effect of Y on Z. However, in the regression of Z on Y
,
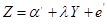the coefficient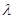 
shows only the association between Y and Z, since some of the variations in Z attributed to Y is due to the confounder X.
We can estimate the total effect of X on Z by the coefficient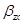 
in the following equation:
.
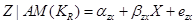We estimate the direct effect of X on Z by:
,
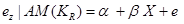where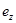 
is the residual Z after removing the effect of Y on Z. The coefficient 
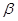is interpreted as the direct effect of X on Z. Interested readers are referred to [11-13] for further discussion about causal effect measurement.
Conclusion
We have provided a short and selective perspective of causal inference, including network analysis, the concept of the assignment mechanism, and effect size estimation. A unique aspect of causal inference compared to traditional applied statistics is captured in the concept of the assignment mechanism. To achieve causal inference, the assignment mechanism must be understood and requires close collaboration between analysts and other biomedical scientists. Taking the AM into account, we are able to identify confounders and measure direct and total causal effects. The assignment mechanism, here formalized in a DAG, can be either known a priori or estimated by an algorithm for directed structures. In this perspective, we assumed that the assignment mechanism is known. In the case of known AM, confounders can be identified from the AM and the measurements remain in a causal setting.
2021 Copyright OAT. All rights reserv
Acknowldgement
This work is supported by a training fellowship from the Keck Center for Interdisciplinary Bioscience Training of the Gulf Coast Consortia (Grant No. RP140113).
References
- Rubin DB (1974) Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies. Journal of Educational Psychology 66: 688–701.
- Rubin DB (2005) Causal inference Using Potential Outcomes: Design, Modeling, Decisions. Journal of the American Statistical Association 100: 322–331.
- Pearl J (2009) Causality: Models, Reasoning, and Inference. Cambridge University Press, New York.
- Dawid P (2012) The Decision-Theoretic Approach to Causal Inference (pp. 25-42) John Wiley & Sons, Ltd.
- Dawid AP (2010) Beware of the DAG!. NIPS Causality: Objectives and Assessment 6: 59-86.
- Yazdani A and Boerwinkle E (2014) Causal inference at the population level. International Journal of Research in Medical Sciences 2: 1368-1370.
- Yazdani A, Boerwinkle E (2015) Causal Inference in the Age of Decision Medicine. J Data Mining Genomics Proteomics 6. [Crossref]
- Rosenbaum P (2009) Design of Observational Studies. Springer Series in Statistics.
- Dawid AP (2007) Fundamentals of statistical causality. Research Report 279, Department of Statistical Science, University College London.
- Lauritzen SL, Dawid AP, Larsen BN, and Leimer HG (1990) Independence Properties of Directed Markov Fields. Networks 20: 491–505.
- Sobel M (2008) Identification of Causal Parameters in Randomized Studies with Mediating Variables. Journal of Educational and Behavioral Statistics 33: 230–231.
- Pearl J (2010) An introduction to causal inference. Int J Biostat 6: Article 7. [Crossref]
- Pearl J (2011) The Causal Foundations of Structural Equation Modeling. Handbook of Structural Equation Modeling. New York: Guilford Press.
