Take a look at the Recent articles

Abstract

Primitive, and invariant across degraded visual settings, topological properties may serve as the basis for object recognition in an ever-changing world. The present study investigated whether human neonates exhibit an intrinsic visual sensitivity for a frequently encountered topological property, the presence or absence of a hole in a 2D shape. Using the familiarization/visual-paired comparison procedures with looking time measurement, we tested forty-three 0 to 4 day-old neonates’ visual discriminability. The infants were randomly assigned to one of the three conditions: Condition 1: a disk vs. a ring (topologically different, geometrically similar), Condition 2: a disk vs. a triangle (topologically equivalent, geometrically different), or Condition 3: a ring vs. an S-like figure (topologically different, and total area equated). Based on infant’s novelty preference scores derived by their looking time, the results showed that neonates were able to differentiate the shapes in Conditions 1 and 3, but not in Condition 2, suggesting a sensitivity for topological but not geometrical property. In sum, the present finding supports the notion that the ability to perceive visual topological information may be readily present at birth, at least for the presence or absence of a hole in a 2D shape.

Key words

 infant visual perception, visual development, topological perception theory, novelty preference, perceptual organization, newborn infants

Introduction

One important adaptive response to objects in the world is the ability to perceive their spatial characteristics at a glance. Topology, as a branch of mathematics seemingly abstract, concerns the basic spatial characteristics that are preserved under continuous and one-to-one transformations. It can be comprehended intuitively by imagining a piece of clay being stretched (or something like a ‘’rubber-sheet’’ distortion) from shape X to shape Y. Under such transformation, the spatial properties preserved from shape X to shape Y are termed topological properties. These include continuity, connectivity, interior/exterior or inside/outside relationship, and the presence/absence and number of holes in an object. For example, a solid disk (○) and a solid triangle (△) are topologically the same shape or equivalent, because a disk and a triangle can be stretched smoothly in space without generating or removing a hole. On the other hand, a solid disk (○) and a hollow ring (◎) are topologically different, although they look similar geometrically as they both have a circular contour. However, a ring contains a hole but a disk contains none; the transformation from a disk to a ring must involve a change in topological property (i.e., creating a hole). The presence/absence of holes in an object marks salient topological information.

Albeit topology may appear abstract and computationally difficult (Marr, 1982), children and adults nevertheless well perceive topological properties and possess implicit knowledge about topology in daily encounters [1,2]. In adult’s visual psychophysics, [3] theory of topological perception proposed that extracting the global topological properties serves as the very starting point of object perception. This standpoint deviates from the part-to-whole view that object perception starts from detecting local features first (local first) [3-5]. Moreover, topological properties are the most stable and robust across transformations and/or under degraded viewing conditions, comparing to other geometric features such as projective, affine, and Euclidean properties [3,6,7]. Thus, the topological properties of an object are rather invariant across views.

Since the topological theory [3] has been introduced, lines of evidence from adult visual psychophysics [8] and brain imaging data [9] have been reported to support its hypothesis. For example, using near-threshold detection/discrimination tasks, researchers found that objects of equivalent topological properties were more likely to be regarded as the same [3,6,8,10]. Moreover, several comparative studies also demonstrated that the sensitivity to topology is not unique to humans: mice [11], goldfish [12], as well as honey-bees [13,14] seem to better discriminate pat-terns differing topologically than geometrically.

Another theory is also relevant to the cognition of topology: [15,16] ‘topological‐primacy thesis’ delineates that children's development and understanding about space starts from using topological information at a younger age. Evidence has shown that children under age four used topological properties (e.g., inside/out-side relation, continuity), instead of Euclidean or geometrical properties (e.g., shape, size), in judging spatial relations among objects [15,17]. They further argued that children were unable to comprehend a Euclidean or linear projective spatial coordinate system until age 8 or 9.

Our main query is: if topological properties are most primitive in processing visual objects and spatial relations, there is great likelihood that the sensitivity for topological properties such as connectedness, continuity, inside/outside relationship, and the presence and number of holes shall be present in early infancy. For instance, the sensitivity for connectedness in 2D pattern organization has been recently explored in young infants. Using a habituation/dishabituation method [18] demonstrated that both 3- to 4-month-olds’ and 6- to 7-month-olds’ were able to use the uniform connectedness (UC) principle [19], one of the most basic perceptual grouping rule, to organize a two-dimensional display. Moreover, using a discrete forced-choice novelty preference technique [20-22], [23] tested 1.5-6-month-olds’ visual sensitivity for shapes differing topologically (e.g. a disk vs. a ring) or geometrically (e.g. a disk vs. a triangle). The results showed that the infants as young as 1.5 months could reliably discriminate between topologically different shapes but not topologically equivalent ones. In a recent study exploring whether the presence or absence of holes forms the essential core of object representation, [24] tested 6-month-old infants’ working memory for objects differing in topological property (i.e., presence or absence of holes). They found that 6 month-old remembered the topology of only one of the two hidden objects, but failed to remember anything about the other object. Their results suggest that topological property indeed play a role in infant’s representation for object identity.

Given the convergent evidence showing an early sensitivity for connectedness and the presence/absence of holes in human infants, as well as the cross-species sensitivity in several lower vertebrates and insects, one may wonder whether detecting topological properties can be an innate propensity in human neonates. To directly address this question, we tested 0 to 4 day-old newborn infants’ visual discriminability for topologically vs. geometrically different shapes with an infant-control familiarization and visual paired comparison procedure. Three between-subject visual discrimination conditions were conducted. In Condition 1, the “topological condition,” we adopted a pair of ring ◎ and disk ○, so that the two figures are geometrically similar (e.g., both have circular contours and curvatures) but topologically different (with/without a hole). In Condition 2, the “geometric condition,” a triangle △ and a disk ○ were adopted. The two shapes differ in geometric form (i.e., curved versus straight contours) and in local features (i.e., with or without corners), but they are topologically equivalent. The Condition 3, the “topological/equal-area condition,” adopted a ring ◎ and an S-like figure, equated in total area and similar in spatial frequencies. They are also topologically different as the ring ◎ has a hole but the S-like figure does not. Our predictions are as follows: if the sensitivity for topological properties is readily present at birth, we predict that neonate infants will be able to discern the ring from the disk in Condition 1, and the ring from the S-like figure in Condition 3, by showing significantly longer fixation time on the novel shape of the test pair after familiarization. Moreover, if the sensitivity for geometric properties develops later, we predict that neonate infants will not be able to discern the ring from the triangle in Condition 2.

Methods

Ethics statement

The present study was conducted in strict accordance with the "Taiwan government's regulations and ICH-GCP guidelines for human participants in behavioral research". Prior to the study session, the parents of all the newborn infants who joined the study were informed about the goal, the content, and the procedures of the observation. Written consent from all the parents of the infant participants were obtained before the observation started. The present study complied with protocols approved by the ethical committee of the Institution Review Board at China Medical University Hospital, Taichung, Taiwan (No. DMR100-IRB-019).

Participants

A total of 43 healthy full-term newborn infants (27 boys, 16 girls) were recruited from China Medical University Children’s Hospital with the help of the Department of Neonatology. Prior to the experiment, informed written consents were obtained by the parents. All infant participants were born within 4 days (mean age = 2.2 days) with an Apgar score of 9 at 1 minute and 10 at 5 minutes after birth. Their birth weight ranged from 2200 g to 3670 g (mean weight =2922 g). In addition, all infants were born within +5 ~ -25 days of their due dates, and had no family history of blindness or health problems at delivery reported by their parents. The infant participants were randomly assigned to one of the three experimental conditions (a ring vs. a disk, a disk vs. a triangle, and an S-like figure vs. a ring). Seven participants were excluded due to failure to complete at least two trials (6) or procedural errors (1). Thus, 36 infants were retained in the final data analysis (11,13, and 12 infants in Condition 1,2, and 3, respectively).

Stimuli and apparatus

As shown in Figure 1, the three conditions were: Pair 1: Disk vs. Ring (topologically different while geometrically similar) (the left panel), Pair 2: Disk vs. Triangle (geometrically different but topologically equivalent) (the middle panel), and Pair 3: Ring vs. S-like figure (topologically different but equated in total area) (the right panel). The stimuli parameters followed those of [6] (the disk and the ring) and [9] (the triangle). The disk had a radius of 10 cm, a perimeter of 31.42 cm, and an area of 78.5 cm². The ring had an outer radius of 10 cm and an inner radius of 5 cm, yielding an outer perimeter of 31.42 cm, an inner perimeter of 15.71 cm, and an area of 58.9 cm². The length of contour of the ring was 47.13 cm in total. The triangle had a height and a base of 10 cm, yielding a perimeter of 32.36 cm and an area of 50.0 cm². The S-like figure had a height and width of 10 cm, with the same total area (i.e. luminance flux) as the ring and a total perimeter of 58.1 cm. Please note that the outer perimeter of the disk, the ring, and the triangle were very similar. The stimuli were cut out from white cardboard papers and mounted onto matte black cardboard background. They were, thus, “cards.” Under typical office room illumination, the white color had a mean luminance of 25.0 cd m-2 and a mean chromaticity at CIE (x= 0.34, y= 0.38), and the black background had a mean luminance of 2.5 cd m-2 and a mean chromaticity at CIE (x= 0.34, y= 0.37), which yielded a high constant Weber’s luminance contrast at the edge. The cardboards were 41cm in length × 26.5cm in width. Set to be viewed from 24 cm from the infant participants, the stimuli extended about a 23.5° visual angle. Each infant underwent a total of four trials (8 cards) in one of the experimental conditions. The “familiarization cards” carried a single figure at the center of black background cardboard. On the cards used in the test phase, two stimuli, one novel and the other familiar, were placed bilaterally with their centers 20.5 cm apart, or 10.25 cm away from the center of the background cardboard. Throughout the experiment, the infant’s looking behavior was recorded throughout the session with a digital camera (Sony DSC-W300) (Figure 1).

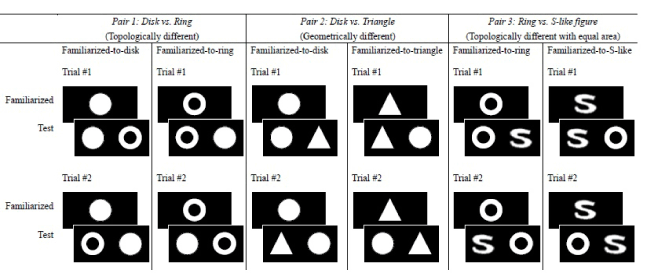
Figure 1. Illustration of the experimental design and the three stimuli conditions: Condition 1: topologically different conditions (left panel), Condition 2: geometrically different conditions (middle panel), and Condition 3: topologically different with total areas equated conditions (right panel). Each trial contained a familiarization phase and a test phase. The infant-control single-stimulus familiarization and visual-paired comparison test procedures was adopted to examine whether newborn infants show novelty preferences after familiarization. Novelty preference score was computed, in which significantly apart from 0.5 implied a successful discrimination.

Procedure

The infant participants were tested either in the birth ward or the maternity ward. They were put lying supine on the bed, held by one of their parents, or a trained experimenter, their face to the stimuli. Randomly assigned to one of the three experimental conditions (a ring vs. a disk, a disk vs. a triangle, and an S-like figure vs. a ring), each participant was to complete a total of four trials. Each trial consisted of a variant of infant-control single-stimulus familiarization phase [25,26], followed by a bilateral visual-paired comparison test phase [27]. During familiarization, a single stimulus was placed at the center of black background cardboard until 25 sec of looking time had been accumulated. During the test phase, two stimuli, one novel and the other familiar, were placed bilaterally with their centers 20.5 cm apart, or 10.25 cm away from the center of the background cardboard. The test phase would not end until 1) both stimuli were fixated at least once and 2) an aggregated looking time of at least 25 sec had been reached. The locations of the familiar and novel figure were counter-balanced between trials. The 8 cards needed to test each participant, 4 trials × 2 phases (1 familiarization + 1 test) had been arranged by another experimenter so that the primary observer was blind to the conditions and locations of the novel stimuli. The right-left position of the novel stimulus and the order of experimental conditions were counterbalanced among participants. The primary observer coded infant’s looking via the recorded video clips offline. Likewise, a secondary observer who was also blind to the stimulus condition coded infant’s looking for about 90% of the total trials. The Pearson correlation coefficients for inter-rater reliability in the test phase were 0.93, 0.89, and 0.90 for the Conditions 1, 2, and 3 respectively, indicating an overall good inter-observer reliability.

Results

Table 1 summarizes the mean looking time at the familiar and the novel stimuli in each condition. The novelty preference scores (in percentage) were calculated as the proportion of the looking time spent on the novel stimulus over the total looking time for both stimuli in the test phase. In Condition 1: the familiarized-to-disk situation, neonates younger than 4-days old looked significantly longer at the novel ring (mean novelty score = 57.2%, t10 = 2.164, p=.026; Cohen’s d=.652). In the complementary familiarized-to-ring situation, interestingly, newborn infants still looked longer at the familiar ring and showed an inverse novelty preference for the familiar ring (mean novelty score = 41.0%, t10=-1.765, p=.050, Cohen’s d=.532 ). Although an inverse novelty preference was found, it nevertheless still indicated a successful discrimination between the ring and the disk.

Novelty Preference Scorea
	M (%)	SE (%)	t #	p
Condition 1: Disk vs. Ring (topologically different)
Familiarized-to-disk	57.2	3.3	2.164	0.026
Familiarized-to-ring	41	5.1	-1.765	0.05
Condition 2: Disk vs. Triangle (topologically equivalent)
Familiarized-to-disk	55	3.5	1.442	0.087
Familiarized-to-triangle	49.3	4.1	-0.172	0.433
Condition 3: Ring vs. S-like figure (topologically different, total areas equated)
Familiarized-to-ring	56.1	3	2.052	0.032
Familiarized-to-S-like figure	58.5	3.7	2.299	0.022

Table 1. The mean novelty preference scores for the three pairs of stimuli.

Note: ^aThe novelty preference score is computed as the percentage of the looking time spent on the novel stimulus over the total looking time for both stimuli in the test phase of a particular trial. # The t statistic is computed as (M – 0.5)/SE.

In Condition 2, the infants did not show significant novelty preference (mean novelty score = 55.0%, t12 =1.441, p = .087) in the familiarized-to-disk situation, nor did they in the familiarized-to-triangle situation (mean novelty score = 49.3%, t12 = -0.172, p = .433). The null results in both familiarization situations suggested that the neonates seemed unable to discriminate the two geometrically different but topologically equivalent figures.

In Condition 3 where a ring and an S-like figure were compared, the infants looked significantly longer at and preferred the S-like figure (mean novelty score = 56.1%, t11 = 2.052, p = .032, Cohen’s d = .592) in the familiarized-to-ring situation. Likewise, in the familiarized-to-S-like figure condition, newborn infants reliably looked longer at and preferred the ring (mean novelty score = 58.5%, t11 = 2.299, p = .022, Cohen’s d = .664). To sum up, newborn infants showed significant preferences for novelty, indicating a successful discrimination between the two topologically different (and with equal areas) figures.

All in all, we found that that 0- to 4-day-old newborn infants could reliably discriminate topologically different figures (i.e., presence or absence of holes) (Conditions 1 and 3); but not geometrically different figures with the same topology (Condition 2).

Discussions

With the single-stimulus familiarization and visual-paired comparison procedures, the present study demonstrated that 0- to 4-day-old human neonates could reliably differentiate between topologically different (i.e. the presence or absence of a hole in the object), but geometrically similar figures (Condition 1), but not the reverse (Condition 2), and even with the total areas equated and spatial frequencies made similar (Condition 3). The results were compatible with [23] findings that infants’ can detect topological differences as young as 1.5 months, while their discrimination of geometric differences was still at chance before 3 months [23,28]. The present study therefore provides evidence for an even earlier sensitivity to topological properties than has been previously thought.

It is worth noting that human neonates’ retina are very immature [29,30]; their visual acuity, contrast sensitivity, and spectral sensitivity improve substantially in the first year of life [31-34]. Given the relatively poor vision at birth, could the neonates’ looking behaviour observed in the present study be driven by other non-topological factors in the stimuli we presented? We will address a few possible candidates such as, contrast and visibility, total luminance flux, luminance difference, and end-stop detector, and rule them one by one in the following paragraph.

First of all, one may argue that neonates may prefer whichever figure yielding the highest contrast, or they may utilize contrast difference on the edge to differentiate the figures. However, this is unlikely in the present study because all the stimuli had the same high Weber’s contrast on the edges, fairly large in visual size, and with well-above-threshold luminance value. It is safe to presume that all the stimuli were clearly visible to the neonatal participants. Secondly, the infants did not simply prefer whichever yielded the highest total luminance flux either, since the disk, with the largest area of white and therefore higher total luminance (78.5 cm²), was not preferred over the triangle (50.0 cm², Condition 2), or the ring (58.9 cm², Condi-tion 1). Thirdly, their preferential looking behavior could not be explained by the differences in luminance between figures, as Condition 2, which yielded the highest difference in figure areas and therefore luminance (28.5 cm²) , was the least evident of preferences (19.6 cm² in Condition 1, and 0 cm2 in Condition 3). Finally, it is also very unlikely to attribute to the neurons in visual cortex that are sensitive to end-stopped contour, as the neonates in the present study could not discriminate between the disk and the triangle in Condition 2.

In the familiarized-to-ring situation of Condition 1, we found a significant below-chance novelty score (an inverse novelty score) for the disk, meaning that the infants still looked longer at the “supposed-to-be-familiar” ring. Our explanation was that it is possible that neonates may have a strong spontaneous preference for the ring and such preference overruled the novelty preference for the disk. This explanation is consistent with the Exp.3 of [23] showing that younger infants (mean age=18.3weeks), other than older infants (mean age = 22.8 weeks), had a spontaneous preference for the ring when paired with a disk. Nevertheless, regardless of the directions, the presence of a spontaneous preference still implies discrimination.

One may also wonder that our results showing neonates could discriminate topologically different figures but not topologically equivalent ones (i.e., a disk vs. a triangle) seems to challenge a well-cited study by [35], who showed that newborn infants could discriminate among simple geometric shapes. Using the habituation procedures with a novel monocular viewing design, [35] reported that newborn infants were able to discriminate among shapes such as crosses, circles, and triangles, as well as same shape with different colors. However, the interocularity and novelty of their paradigm may have been responsible for their exciting message that infants’ perceptual ability emerged earlier than had been thought. Classic views on neonatal color vision proposed that the retinal system was so immature at birth [30] that “true” color perception is not present until about 7 weeks of age [36,37]. Because the methodologies and the stimulus parameters used in the present study and in [35] are too divert, again, it is hard to make direct comparisons between the two studies.

Nevertheless, the present findings are in accordance with several recent studies on young infants’ perceptual organization. Using the habituation paradigm, [18] found that both 3- to 4-month-olds’ and 6- to 7-month-olds’ could utilize the uniform connectedness principle to organize static two-dimensional displays, i.e. they could tell the subtle differences between two visual elements that were connected or disconnected. Moreover, using the familiarization/paired-comparison procedures, [26] reported that neonates can categorize the so-called “closed” and “open” geometric forms. We argue that they provided evidence for an early sensitivity to topologically properties as their between-category exemplars (either the “closed” or the “open” forms) were also topologically different. “Closure” was, in their terms, “feature[s] that can be extracted by the visual system [as] early as a primitive property,” or “…likely in light of the studies with adults that indicate that closure-openness is perceived as a primitive global topological property [3,6] or configural-wholistic” [38-40] [26].

Conclusions

In summary, the present study has three empirical findings. First, human neonates seem to have an intrinsic capacity to discriminate topologically different visual patterns, at least for the ones with or without a hole. Second, infants’ discriminability for topologically different patterns (a ring vs. a disk and a ring vs. an S-like figure) cannot be attributed to other low level factors such as their responsiveness to the luminance of the stimuli. Third, an inverse novelty preference for the disk in the familiarized-to-ring condition of Exp. 1 might be attributed to the overruling of a spontaneous preference for the ring; nevertheless, a spontaneous preference still implies successful discrimination. Moreover, our findings have a few theoretical implications. First of all, the pattern of results is consistent with the key hypothesis of the topological perception theory [3] that extracting global topological properties serves as the starting point of object processing in the visual system. On the other hand, detecting or extracting local geometric properties, at least for curved versus straight contours, may not be an intrinsic capacity of the neonates’ visual system. Secondly, the finding that newborn infants are more sensitive to the global topological property is also consistent with the differentiation/ learning view of perceptual development [41]. In this view, infants’ perceptual development is regarded as a differentiation process; experience and physiological maturation leads to extraction of finer detail from the environment. Lastly, as also found in mice, goldfish, zebra fish and honeybees, nature seems to endow human neonates with the ability to perceive topological properties through millions of years of evolutional mechanisms. One important advantage of topological properties is that they are very stable and robust across transformations and under degraded viewing conditions. In this sense, an intrinsic sensitivity for topological properties could be advantageous for survival for neonates who are born to an ever changing world with an immature visual system. Apparently, the repertoire of topological properties is much broader than the presence or absence of holes in a 2D shape. Other equally important topological features such as connectivity and inside/outside relationship also deserve investigations in this line of research. To conclude, the present study indicates that human neonates seem to have an intrinsic sensitivity to perceive topological property.

Acknowledgements

This project was supported in part by Taiwanese Ministry of Science and Technology Grants: NSC 99-2410-H-039-003-MY3 and MOST 103-2410-H-039-002-MY3 to Dr. S. H. L. Chien and in part by a Taiwanese Student Research Grant NSC 99-2815-C-039-075-H to the first author Y. L. Lin. The authors would like to thank the newborn infants and their parents for participating the study, Dr. Bai-Horn Su for his generous support, and Ms. Hsin-Yueh Hsu, Ms. Wen_Ting Yeh, and Ms. Y

Abstract

Primitive, and invariant across degraded visual settings, topological properties may serve as the basis for object recognition in an ever-changing world. The present study investigated whether human neonates exhibit an intrinsic visual sensitivity for a frequently encountered topological property, the presence or absence of a hole in a 2D shape. Using the familiarization/visual-paired comparison procedures with looking time measurement, we tested forty-three 0 to 4 day-old neonates’ visual discriminability. The infants were randomly assigned to one of the three conditions: Condition 1: a disk vs. a ring (topologically different, geometrically similar), Condition 2: a disk vs. a triangle (topologically equivalent, geometrically different), or Condition 3: a ring vs. an S-like figure (topologically different, and total area equated). Based on infant’s novelty preference scores derived by their looking time, the results showed that neonates were able to differentiate the shapes in Conditions 1 and 3, but not in Condition 2, suggesting a sensitivity for topological but not geometrical property. In sum, the present finding supports the notion that the ability to perceive visual topological information may be readily present at birth, at least for the presence or absence of a hole in a 2D shape.

Key words

 infant visual perception, visual development, topological perception theory, novelty preference, perceptual organization, newborn infants

Introduction

One important adaptive response to objects in the world is the ability to perceive their spatial characteristics at a glance. Topology, as a branch of mathematics seemingly abstract, concerns the basic spatial characteristics that are preserved under continuous and one-to-one transformations. It can be comprehended intuitively by imagining a piece of clay being stretched (or something like a ‘’rubber-sheet’’ distortion) from shape X to shape Y. Under such transformation, the spatial properties preserved from shape X to shape Y are termed topological properties. These include continuity, connectivity, interior/exterior or inside/outside relationship, and the presence/absence and number of holes in an object. For example, a solid disk (○) and a solid triangle (△) are topologically the same shape or equivalent, because a disk and a triangle can be stretched smoothly in space without generating or removing a hole. On the other hand, a solid disk (○) and a hollow ring (◎) are topologically different, although they look similar geometrically as they both have a circular contour. However, a ring contains a hole but a disk contains none; the transformation from a disk to a ring must involve a change in topological property (i.e., creating a hole). The presence/absence of holes in an object marks salient topological information.

Albeit topology may appear abstract and computationally difficult (Marr, 1982), children and adults nevertheless well perceive topological properties and possess implicit knowledge about topology in daily encounters [1,2]. In adult’s visual psychophysics, [3] theory of topological perception proposed that extracting the global topological properties serves as the very starting point of object perception. This standpoint deviates from the part-to-whole view that object perception starts from detecting local features first (local first) [3-5]. Moreover, topological properties are the most stable and robust across transformations and/or under degraded viewing conditions, comparing to other geometric features such as projective, affine, and Euclidean properties [3,6,7]. Thus, the topological properties of an object are rather invariant across views.

Since the topological theory [3] has been introduced, lines of evidence from adult visual psychophysics [8] and brain imaging data [9] have been reported to support its hypothesis. For example, using near-threshold detection/discrimination tasks, researchers found that objects of equivalent topological properties were more likely to be regarded as the same [3,6,8,10]. Moreover, several comparative studies also demonstrated that the sensitivity to topology is not unique to humans: mice [11], goldfish [12], as well as honey-bees [13,14] seem to better discriminate pat-terns differing topologically than geometrically.

Another theory is also relevant to the cognition of topology: [15,16] ‘topological‐primacy thesis’ delineates that children's development and understanding about space starts from using topological information at a younger age. Evidence has shown that children under age four used topological properties (e.g., inside/out-side relation, continuity), instead of Euclidean or geometrical properties (e.g., shape, size), in judging spatial relations among objects [15,17]. They further argued that children were unable to comprehend a Euclidean or linear projective spatial coordinate system until age 8 or 9.

Our main query is: if topological properties are most primitive in processing visual objects and spatial relations, there is great likelihood that the sensitivity for topological properties such as connectedness, continuity, inside/outside relationship, and the presence and number of holes shall be present in early infancy. For instance, the sensitivity for connectedness in 2D pattern organization has been recently explored in young infants. Using a habituation/dishabituation method [18] demonstrated that both 3- to 4-month-olds’ and 6- to 7-month-olds’ were able to use the uniform connectedness (UC) principle [19], one of the most basic perceptual grouping rule, to organize a two-dimensional display. Moreover, using a discrete forced-choice novelty preference technique [20-22], [23] tested 1.5-6-month-olds’ visual sensitivity for shapes differing topologically (e.g. a disk vs. a ring) or geometrically (e.g. a disk vs. a triangle). The results showed that the infants as young as 1.5 months could reliably discriminate between topologically different shapes but not topologically equivalent ones. In a recent study exploring whether the presence or absence of holes forms the essential core of object representation, [24] tested 6-month-old infants’ working memory for objects differing in topological property (i.e., presence or absence of holes). They found that 6 month-old remembered the topology of only one of the two hidden objects, but failed to remember anything about the other object. Their results suggest that topological property indeed play a role in infant’s representation for object identity.

Given the convergent evidence showing an early sensitivity for connectedness and the presence/absence of holes in human infants, as well as the cross-species sensitivity in several lower vertebrates and insects, one may wonder whether detecting topological properties can be an innate propensity in human neonates. To directly address this question, we tested 0 to 4 day-old newborn infants’ visual discriminability for topologically vs. geometrically different shapes with an infant-control familiarization and visual paired comparison procedure. Three between-subject visual discrimination conditions were conducted. In Condition 1, the “topological condition,” we adopted a pair of ring ◎ and disk ○, so that the two figures are geometrically similar (e.g., both have circular contours and curvatures) but topologically different (with/without a hole). In Condition 2, the “geometric condition,” a triangle △ and a disk ○ were adopted. The two shapes differ in geometric form (i.e., curved versus straight contours) and in local features (i.e., with or without corners), but they are topologically equivalent. The Condition 3, the “topological/equal-area condition,” adopted a ring ◎ and an S-like figure, equated in total area and similar in spatial frequencies. They are also topologically different as the ring ◎ has a hole but the S-like figure does not. Our predictions are as follows: if the sensitivity for topological properties is readily present at birth, we predict that neonate infants will be able to discern the ring from the disk in Condition 1, and the ring from the S-like figure in Condition 3, by showing significantly longer fixation time on the novel shape of the test pair after familiarization. Moreover, if the sensitivity for geometric properties develops later, we predict that neonate infants will not be able to discern the ring from the triangle in Condition 2.

Methods

Ethics statement

The present study was conducted in strict accordance with the "Taiwan government's regulations and ICH-GCP guidelines for human participants in behavioral research". Prior to the study session, the parents of all the newborn infants who joined the study were informed about the goal, the content, and the procedures of the observation. Written consent from all the parents of the infant participants were obtained before the observation started. The present study complied with protocols approved by the ethical committee of the Institution Review Board at China Medical University Hospital, Taichung, Taiwan (No. DMR100-IRB-019).

Participants

A total of 43 healthy full-term newborn infants (27 boys, 16 girls) were recruited from China Medical University Children’s Hospital with the help of the Department of Neonatology. Prior to the experiment, informed written consents were obtained by the parents. All infant participants were born within 4 days (mean age = 2.2 days) with an Apgar score of 9 at 1 minute and 10 at 5 minutes after birth. Their birth weight ranged from 2200 g to 3670 g (mean weight =2922 g). In addition, all infants were born within +5 ~ -25 days of their due dates, and had no family history of blindness or health problems at delivery reported by their parents. The infant participants were randomly assigned to one of the three experimental conditions (a ring vs. a disk, a disk vs. a triangle, and an S-like figure vs. a ring). Seven participants were excluded due to failure to complete at least two trials (6) or procedural errors (1). Thus, 36 infants were retained in the final data analysis (11,13, and 12 infants in Condition 1,2, and 3, respectively).

Stimuli and apparatus

As shown in Figure 1, the three conditions were: Pair 1: Disk vs. Ring (topologically different while geometrically similar) (the left panel), Pair 2: Disk vs. Triangle (geometrically different but topologically equivalent) (the middle panel), and Pair 3: Ring vs. S-like figure (topologically different but equated in total area) (the right panel). The stimuli parameters followed those of [6] (the disk and the ring) and [9] (the triangle). The disk had a radius of 10 cm, a perimeter of 31.42 cm, and an area of 78.5 cm². The ring had an outer radius of 10 cm and an inner radius of 5 cm, yielding an outer perimeter of 31.42 cm, an inner perimeter of 15.71 cm, and an area of 58.9 cm². The length of contour of the ring was 47.13 cm in total. The triangle had a height and a base of 10 cm, yielding a perimeter of 32.36 cm and an area of 50.0 cm². The S-like figure had a height and width of 10 cm, with the same total area (i.e. luminance flux) as the ring and a total perimeter of 58.1 cm. Please note that the outer perimeter of the disk, the ring, and the triangle were very similar. The stimuli were cut out from white cardboard papers and mounted onto matte black cardboard background. They were, thus, “cards.” Under typical office room illumination, the white color had a mean luminance of 25.0 cd m-2 and a mean chromaticity at CIE (x= 0.34, y= 0.38), and the black background had a mean luminance of 2.5 cd m-2 and a mean chromaticity at CIE (x= 0.34, y= 0.37), which yielded a high constant Weber’s luminance contrast at the edge. The cardboards were 41cm in length × 26.5cm in width. Set to be viewed from 24 cm from the infant participants, the stimuli extended about a 23.5° visual angle. Each infant underwent a total of four trials (8 cards) in one of the experimental conditions. The “familiarization cards” carried a single figure at the center of black background cardboard. On the cards used in the test phase, two stimuli, one novel and the other familiar, were placed bilaterally with their centers 20.5 cm apart, or 10.25 cm away from the center of the background cardboard. Throughout the experiment, the infant’s looking behavior was recorded throughout the session with a digital camera (Sony DSC-W300) (Figure 1).

Procedure

The infant participants were tested either in the birth ward or the maternity ward. They were put lying supine on the bed, held by one of their parents, or a trained experimenter, their face to the stimuli. Randomly assigned to one of the three experimental conditions (a ring vs. a disk, a disk vs. a triangle, and an S-like figure vs. a ring), each participant was to complete a total of four trials. Each trial consisted of a variant of infant-control single-stimulus familiarization phase [25,26], followed by a bilateral visual-paired comparison test phase [27]. During familiarization, a single stimulus was placed at the center of black background cardboard until 25 sec of looking time had been accumulated. During the test phase, two stimuli, one novel and the other familiar, were placed bilaterally with their centers 20.5 cm apart, or 10.25 cm away from the center of the background cardboard. The test phase would not end until 1) both stimuli were fixated at least once and 2) an aggregated looking time of at least 25 sec had been reached. The locations of the familiar and novel figure were counter-balanced between trials. The 8 cards needed to test each participant, 4 trials × 2 phases (1 familiarization + 1 test) had been arranged by another experimenter so that the primary observer was blind to the conditions and locations of the novel stimuli. The right-left position of the novel stimulus and the order of experimental conditions were counterbalanced among participants. The primary observer coded infant’s looking via the recorded video clips offline. Likewise, a secondary observer who was also blind to the stimulus condition coded infant’s looking for about 90% of the total trials. The Pearson correlation coefficients for inter-rater reliability in the test phase were 0.93, 0.89, and 0.90 for the Conditions 1, 2, and 3 respectively, indicating an overall good inter-observer reliability.

Results

Table 1 summarizes the mean looking time at the familiar and the novel stimuli in each condition. The novelty preference scores (in percentage) were calculated as the proportion of the looking time spent on the novel stimulus over the total looking time for both stimuli in the test phase. In Condition 1: the familiarized-to-disk situation, neonates younger than 4-days old looked significantly longer at the novel ring (mean novelty score = 57.2%, t10 = 2.164, p=.026; Cohen’s d=.652). In the complementary familiarized-to-ring situation, interestingly, newborn infants still looked longer at the familiar ring and showed an inverse novelty preference for the familiar ring (mean novelty score = 41.0%, t10=-1.765, p=.050, Cohen’s d=.532 ). Although an inverse novelty preference was found, it nevertheless still indicated a successful discrimination between the ring and the disk.

In Condition 2, the infants did not show significant novelty preference (mean novelty score = 55.0%, t12 =1.441, p = .087) in the familiarized-to-disk situation, nor did they in the familiarized-to-triangle situation (mean novelty score = 49.3%, t12 = -0.172, p = .433). The null results in both familiarization situations suggested that the neonates seemed unable to discriminate the two geometrically different but topologically equivalent figures.

In Condition 3 where a ring and an S-like figure were compared, the infants looked significantly longer at and preferred the S-like figure (mean novelty score = 56.1%, t11 = 2.052, p = .032, Cohen’s d = .592) in the familiarized-to-ring situation. Likewise, in the familiarized-to-S-like figure condition, newborn infants reliably looked longer at and preferred the ring (mean novelty score = 58.5%, t11 = 2.299, p = .022, Cohen’s d = .664). To sum up, newborn infants showed significant preferences for novelty, indicating a successful discrimination between the two topologically different (and with equal areas) figures.

All in all, we found that that 0- to 4-day-old newborn infants could reliably discriminate topologically different figures (i.e., presence or absence of holes) (Conditions 1 and 3); but not geometrically different figures with the same topology (Condition 2).

Discussions

With the single-stimulus familiarization and visual-paired comparison procedures, the present study demonstrated that 0- to 4-day-old human neonates could reliably differentiate between topologically different (i.e. the presence or absence of a hole in the object), but geometrically similar figures (Condition 1), but not the reverse (Condition 2), and even with the total areas equated and spatial frequencies made similar (Condition 3). The results were compatible with [23] findings that infants’ can detect topological differences as young as 1.5 months, while their discrimination of geometric differences was still at chance before 3 months [23,28]. The present study therefore provides evidence for an even earlier sensitivity to topological properties than has been previously thought.

It is worth noting that human neonates’ retina are very immature [29,30]; their visual acuity, contrast sensitivity, and spectral sensitivity improve substantially in the first year of life [31-34]. Given the relatively poor vision at birth, could the neonates’ looking behaviour observed in the present study be driven by other non-topological factors in the stimuli we presented? We will address a few possible candidates such as, contrast and visibility, total luminance flux, luminance difference, and end-stop detector, and rule them one by one in the following paragraph.

2021 Copyright OAT. All rights reserv

First of all, one may argue that neonates may prefer whichever figure yielding the highest contrast, or they may utilize contrast difference on the edge to differentiate the figures. However, this is unlikely in the present study because all the stimuli had the same high Weber’s contrast on the edges, fairly large in visual size, and with well-above-threshold luminance value. It is safe to presume that all the stimuli were clearly visible to the neonatal participants. Secondly, the infants did not simply prefer whichever yielded the highest total luminance flux either, since the disk, with the largest area of white and therefore higher total luminance (78.5 cm²), was not preferred over the triangle (50.0 cm², Condition 2), or the ring (58.9 cm², Condi-tion 1). Thirdly, their preferential looking behavior could not be explained by the differences in luminance between figures, as Condition 2, which yielded the highest difference in figure areas and therefore luminance (28.5 cm²) , was the least evident of preferences (19.6 cm² in Condition 1, and 0 cm2 in Condition 3). Finally, it is also very unlikely to attribute to the neurons in visual cortex that are sensitive to end-stopped contour, as the neonates in the present study could not discriminate between the disk and the triangle in Condition 2.

In the familiarized-to-ring situation of Condition 1, we found a significant below-chance novelty score (an inverse novelty score) for the disk, meaning that the infants still looked longer at the “supposed-to-be-familiar” ring. Our explanation was that it is possible that neonates may have a strong spontaneous preference for the ring and such preference overruled the novelty preference for the disk. This explanation is consistent with the Exp.3 of [23] showing that younger infants (mean age=18.3weeks), other than older infants (mean age = 22.8 weeks), had a spontaneous preference for the ring when paired with a disk. Nevertheless, regardless of the directions, the presence of a spontaneous preference still implies discrimination.

One may also wonder that our results showing neonates could discriminate topologically different figures but not topologically equivalent ones (i.e., a disk vs. a triangle) seems to challenge a well-cited study by [35], who showed that newborn infants could discriminate among simple geometric shapes. Using the habituation procedures with a novel monocular viewing design, [35] reported that newborn infants were able to discriminate among shapes such as crosses, circles, and triangles, as well as same shape with different colors. However, the interocularity and novelty of their paradigm may have been responsible for their exciting message that infants’ perceptual ability emerged earlier than had been thought. Classic views on neonatal color vision proposed that the retinal system was so immature at birth [30] that “true” color perception is not present until about 7 weeks of age [36,37]. Because the methodologies and the stimulus parameters used in the present study and in [35] are too divert, again, it is hard to make direct comparisons between the two studies.

Nevertheless, the present findings are in accordance with several recent studies on young infants’ perceptual organization. Using the habituation paradigm, [18] found that both 3- to 4-month-olds’ and 6- to 7-month-olds’ could utilize the uniform connectedness principle to organize static two-dimensional displays, i.e. they could tell the subtle differences between two visual elements that were connected or disconnected. Moreover, using the familiarization/paired-comparison procedures, [26] reported that neonates can categorize the so-called “closed” and “open” geometric forms. We argue that they provided evidence for an early sensitivity to topologically properties as their between-category exemplars (either the “closed” or the “open” forms) were also topologically different. “Closure” was, in their terms, “feature[s] that can be extracted by the visual system [as] early as a primitive property,” or “…likely in light of the studies with adults that indicate that closure-openness is perceived as a primitive global topological property [3,6] or configural-wholistic” [38-40] [26].

Conclusions

In summary, the present study has three empirical findings. First, human neonates seem to have an intrinsic capacity to discriminate topologically different visual patterns, at least for the ones with or without a hole. Second, infants’ discriminability for topologically different patterns (a ring vs. a disk and a ring vs. an S-like figure) cannot be attributed to other low level factors such as their responsiveness to the luminance of the stimuli. Third, an inverse novelty preference for the disk in the familiarized-to-ring condition of Exp. 1 might be attributed to the overruling of a spontaneous preference for the ring; nevertheless, a spontaneous preference still implies successful discrimination. Moreover, our findings have a few theoretical implications. First of all, the pattern of results is consistent with the key hypothesis of the topological perception theory [3] that extracting global topological properties serves as the starting point of object processing in the visual system. On the other hand, detecting or extracting local geometric properties, at least for curved versus straight contours, may not be an intrinsic capacity of the neonates’ visual system. Secondly, the finding that newborn infants are more sensitive to the global topological property is also consistent with the differentiation/ learning view of perceptual development [41]. In this view, infants’ perceptual development is regarded as a differentiation process; experience and physiological maturation leads to extraction of finer detail from the environment. Lastly, as also found in mice, goldfish, zebra fish and honeybees, nature seems to endow human neonates with the ability to perceive topological properties through millions of years of evolutional mechanisms. One important advantage of topological properties is that they are very stable and robust across transformations and under degraded viewing conditions. In this sense, an intrinsic sensitivity for topological properties could be advantageous for survival for neonates who are born to an ever changing world with an immature visual system. Apparently, the repertoire of topological properties is much broader than the presence or absence of holes in a 2D shape. Other equally important topological features such as connectivity and inside/outside relationship also deserve investigations in this line of research. To conclude, the present study indicates that human neonates seem to have an intrinsic sensitivity to perceive topological property.

Acknowledgements

This project was supported in part by Taiwanese Ministry of Science and Technology Grants: NSC 99-2410-H-039-003-MY3 and MOST 103-2410-H-039-002-MY3 to Dr. S. H. L. Chien and in part by a Taiwanese Student Research Grant NSC 99-2815-C-039-075-H to the first author Y. L. Lin. The authors would like to thank the newborn infants and their parents for participating the study, Dr. Bai-Horn Su for his generous support, and Ms. Hsin-Yueh Hsu, Ms. Wen_Ting Yeh, and Ms. Yun Lin for their assistance in data coding and collection.

un Lin for their assistance in data coding and collection.

References

1. Casati R (2002) Topology and cognition. Encyclopedia of cognitive science 410–417. London: McMillan.
2. Casati R (2009) does topological perception rest on a misconception about topology? Philo-sophical Psychology 22: 77–81.  
3. Chen L (1982) Topological structure in visual perception. Science 218: 699-700. [Crossref]
4. Treisman A (1988) Features and objects: the fourteenth Bartlett memorial lecture. Q J Exp Psychol A 40: 201-237. [Crossref]
5. Wolfe JM (2003) Moving towards solutions to some enduring controversies in visual search. Trends Cogn Sci 7: 70-76. [Crossref]
6. Chen L (1990) Holes and wholes: a reply to Rubin and Kanwisher. Percept Psychophys 47: 47-53. [Crossref]
7. He S (2008) Holes, objects, and the left hemisphere. Proc Natl Acad Sci U S A 105: 1103-1104. [Crossref]
8. Chen L (2005) The topological approach to perceptual organization. Visual Cognition 12: 553-567.
9. Wang B, Zhou TG, Zhuo Y, Chen L (2007) Global topological dominance in the left hemisphere. Proc Natl Acad Sci U S A 104: 21014-21019. [Crossref]
10. Rubin JM, Kanwisher N (1985) Topological perception: holes in an experiment. Percept Psychophys 37: 179-180. [Crossref]
11. Zhu J, Guo XY, MA Y, Ren F (2010) Different topological properties pattern recognition in mice. Progress in Biochemistry and Biophysics 06.
12. Ma MM, Qian C, Liu Z, Chen L (2012) Global perception in small brains: Topological pattern recognition in goldfish. Program No. 262.21. Neuroscience 2012 Abstracts. New Orleans, Louisiana: Society for Neuroscience.
13. Chen L, Zhang S, Srinivasan MV (2003) Global perception in small brains: Topological pattern recognition in honey bees. Proceedings of the National Academy of Sciences 100: 6884-6889.
14. Pomerantz JR (2003) Wholes, holes, and basic features in vision. Trends Cogn Sci 7: 471-473. [Crossref]
15. Piaget J, Inhelder B (1956) The child's conception of space. London: Routiedge & Kegan Paul.
16. Piaget J, Inhelder B (1967) The child’s conception of space. New York, NY: Norton.
17. Darke I (1982) A review of research related to the topological primacy thesis. Educational Studies in Mathematics 1: 119-142.
18. Hayden A, Bhatt RS, Quinn PC (2006) Infants' sensitivity to uniform connectedness as a cue for perceptual organization. Psychon Bull Rev 13: 257-261. [Crossref]
19. Palmer S, Rock I (1994) Rethinking perceptual organization: The role of uniform connectedness. Psychon Bull Rev 1: 29-55. [Crossref]
20. Chien SH, Palmer J, Teller DY (2003) Infant lightness perception: do 4-month-old infants follow Wallach's ratio rule? Psychol Sci 14: 291-295. [Crossref] 
21. Civan A, Teller DY, Palmer J (2005) Relations between spontaneous preferences, familiarized preferences, and novelty effects: Measurements with forced-choice techniques. Infancy 7: 111 -142.
22. Chien SH, Hsu HY, Su BH (2010) Discriminating "top-heavy" versus "bottom-heavy" geometric patterns in 2- to 4.5-month-old infants. Vision Res 50: 2029-2036. [Crossref]
23. Chien SH, Lin YL, Qian W, Zhou K, Lin MK, et al. (2012) With or without a hole: young infants' sensitivity for topological versus geometric property. Perception 41: 305-318. [Crossref]
24. Kibbe MM, Leslie AM (2016) The ring that does not bind: Topological class in infants’ working memory for objects. Cognitive Development 38: 1-9.
25. Angela M, Brown AM, Yamamoto M (1986) Visual acuity in newborn and preterm infants measured with grating acuity cards. Am J Ophthalmol 102: 245-253. [Crossref] 
26. Turati C, Simion F, Zanon L (2003) Newborns’ perceptual categorization for closed and open geometric forms. Infancy 309-325.
27. Fagan JF 3rd (1970) Memory in the infant. J Exp Child Psychol 9: 217-226. [Crossref]
28. Chien SHL, Lin YL, Chen L (2011) Development of visual sensitivity for topological versus geometric properties in early infancy. Poster presented at the 2011 Annual Meeting of the Asian-Pacific Conference on Vision, Hong Kong, China.
29. Abramov I, Gordon J, Hendrickson A, Hainline L, Dobson V, et al. (1982) The retina of the newborn human infant. Science 217: 265-267. [Crossref]
30. Yuodelis C, Hendrickson A (1986) A qualitative and quantitative analysis of the human fovea during development. Vision Res 26: 847-855. [Crossref]
31. Peeples DR, Teller DY (1978) White-adapted photopic spectral sensitivity in human infants. Vision Res 18: 49-53. [Crossref]
32. Atkinson J, Braddick O (1989) Development of basic visual functions. In A. Slater & G.Bremner (Eds.), Infant Development (pp. 7-61) Hove, England: Lawrence Erlbaum Associates, Inc.
33. Banks MS, Shannon ES (1993) Spatial and chromatic visual efficiency in human neonates. In C.E. Granrud (Ed.), Carnegie-Mellon Symposium on Cognitive Psychology. (pp. 1-46). Hillsdale, NJ: Erlbaum.
34. Teller DY (1997) First glances: the vision of infants. the Friedenwald lecture. Invest Ophthalmol Vis Sci 38: 2183-2203. [Crossref]
35. Slater A, Morison V, Rose D (1983) Locus of habituation in the human newborn. Perception 12: 593-598. [Crossref]
36. Peeles DR, Teller DY (1975) Color vision and brightness discrimination in two-month-old human infants. Science 189: 1102-1103. [Crossref] 
37. Teller DY, Peeples DR, Sekel M (1978) Discrimination of chromatic from white light by two-month-old human infants. Vision Res 18: 41-48. [Crossref]
38. Kimchi R (1994) The role of wholistic/configural properties versus global properties in visual form perception. Perception 23: 489-504. [Crossref]
39. Kimchi R, Bloch B (1998) Dominance of configural properties in visual form perception. Psychonomic Bulletin & Review S: 135-139.
40. Frick JE, Colombo J, Allen JR (2000) Temporal sequence of global-local processing in3-month-old infants. Infancy 375-386.
41. Gibson E (1969) Principles of perceptual learning and development. New York: Appleton-. Century-Crofts.