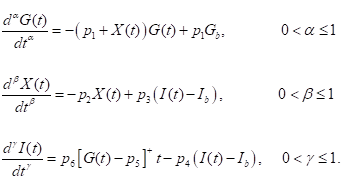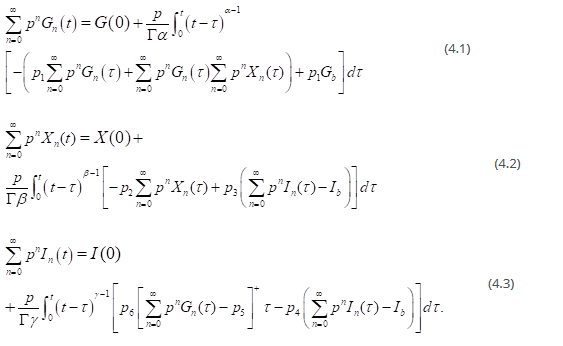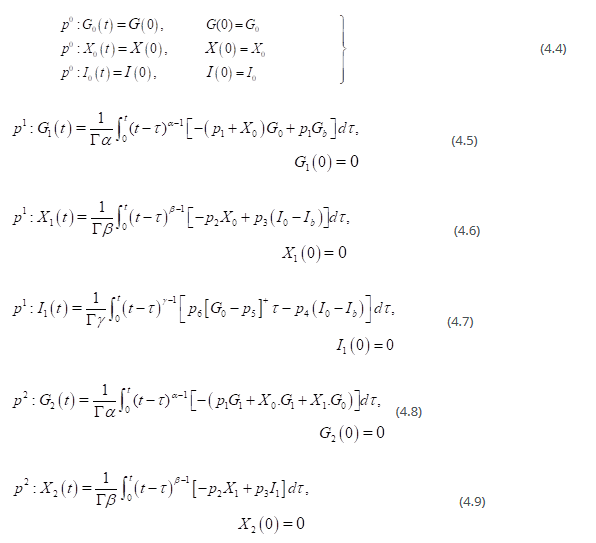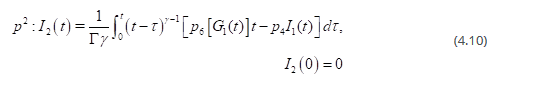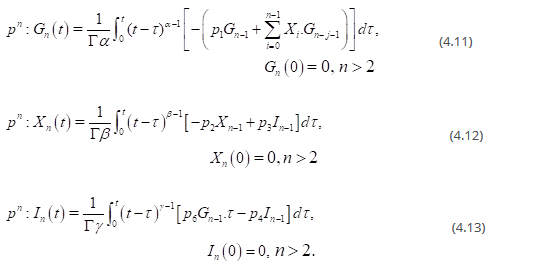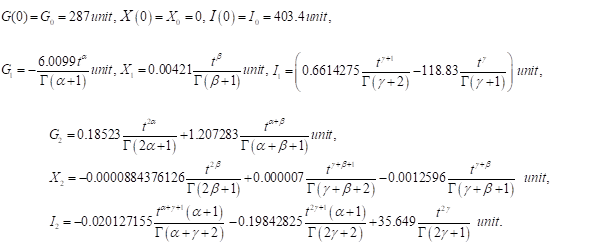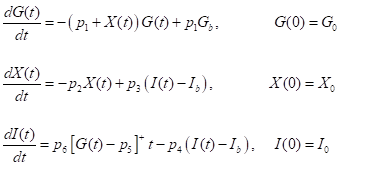In this paper, we use the Homotopy Decomposition Method (HDM), to solve fractional nonlinear differential equations systems that arise in Bergman’s minimal model, used to describe blood glucose and insulin metabolism, after intravenous tolerance testing. Consequent numerical simulations representing Bergman approximate solutions demonstrate they are indeed continuous functions of derivatives. Not only is the HDM extremely versatile throughout in solving nonlinear fractional partial differential equations systems, but also, despite its direct simplicity, does turn out to be highly efficient, as thoroughly shown below.
Bergman’s minimal model, homotopy decomposition method, he’s polynomials, fractional differential equation
During the nineties, when faced with blood or blood constituent’s dynamical transport phenomena, researchers almost always tried their hand at applying classical theory tools to describe related processes, (see refs in [1-4]). Certainly successful as those effort were, attempts to see biological and fluid physiological flavor phenomena related to transport processes may be looked from stochastic points of views, emphasizing the pursuit of individual particles, balanced with the particle ensemble approach [5,6], in light of convective diffusion equations. A decade later, such efforts were further enriched with
serious and rather successful attempts at connecting state of the art approaches at the time with Naviers-Stokes and Burgers equations with intentions to study turbulence, via the Hopf-Cole transformation setup [7-10]. Now, nearly a quarter of a century on since the Biophysical Journal article [1], having to some extent manipulated tools from the classical Eulerean Continuum Calculus, and the Lagrangian Stochastic Calculus, and expanded techniques that we propose to term: the Hopf-Cole Calculus, here in a total change of gear, the stage is set for no other calculi tools, but those of Fractional Calculus, (see for instance [11-18]).
In this paper, we consider the Fractional setup of Bergman minimal model for blood glucose-insulin interactions. For a practical purpose we solve the consequent system of fractional partial differential equations moderate the glucose-insulin metabolism, after intravenous tolerance testing. Worthy is it to note here, that typically, to describe physiological and biological processes, standard mathematical models of integer-order derivatives, including nonlinear models, do not always work adequately in many such cases, and the Bergman minimal model turns out to be of no exception. That is why, we found it necessary to implement the non-classical tools, which proved very useful and pragmatic in various fields such as modeling physical and engineering processes [7,19,20]. In the foreword, we propose to make use of the HDM [21-23], a relatively new analytical technique. The technique is described and illustrated in a computationally numerical set up.
Bergman’s minimal model [24-28] is a one compartment model, meaning that the body is described as a compartment with a basal concentration of glucose and insulin. The minimal model has two variations. The first describe glucose kinetics, how blood glucose concentration reacts with blood insulin concentration. Reciprocally, the alternative variation itemizes the insulin kinetics, which describes the blood insulin concentration reactions with glucose concentration in the blood. Both models alternatives take insulin and glucose data as an input, respectively. Both models have been used mostly to interpret the blood glucose insulin interactions during the Glucose Tolerance Test [25,26].
Below the Bergman minimal model is presented in light of the following in view of the nomenclature of parameters.
Nomenclature of Parameters for Bergman's Minimal Model.
|
Parameter
|
Unit
|
Description
|
|
G(t)
|
[mg/dL]
|
Blood glucose concentration
|
|
X(t)
|
[1/min]
|
The effect of active insulin
|
|
I(t)
|
[mU/L]
|
Blood insulin concentration
|
|
Gb
|
[mg/dL]
|
Basal blood glucose concentration
|
|
Ib
|
[mU/L]
|
Basal blood insulin concentration
|
|
p1
|
[1/min]
|
Insulin independent glucose clearance rate
|
|
p2
|
[1/min]
|
Active insulin clearance rate (upt. decrease)
|
|
p3
|
[L/(min2mU)]
|
Increase in uptake ability caused by insulin
|
|
p4
|
[1/min]
|
Decay rate of blood insulin
|
|
p5
|
[mg/dL]
|
The target glucose level
|
|
p6
|
[mUdL/Lmgmin]
|
Pancreatic release rate after glucose bolus
|
In order to describe the time course of these concentrations, the minimal model of the glucose insulin kinetics has been proposed. We will use the standard formulation of the minimal model represented by the following system of differential equations,
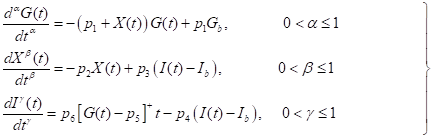 (1.1)
(1.1)
subject to the initial conditions,
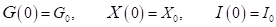 (1.2)
(1.2)
This model can be used to describe the pancreas as the source of insulin. In a healthy individual a small amount of insulin is always created and cleared [24]. This helps to keep the basal concentration Ib. The glucose independent production and clearance of insulin is proportional to the blood insulin concentration. If the insulin level is above the base level concentration, clearance is increased. On the other hand, if the insulin level is below basal concentration, production increases. When the glucose level gets high, the pancreas reacts by releasing more insulin, at a given rate. To explain this mathematically one has to derive a function describing the reaction of the pancreas. This function was derived by Bergman et al., [27], and adjusted by Gaetano et al. [25] to become,
Pancreas(t)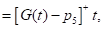 where
where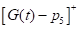 = Maximum (
= Maximum (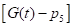 , 0), (1.3)
, 0), (1.3)
The layout of this paper is as follows: a brief history and properties of fractional derivatives are given in section 2, followed by the HDM a description of the application mechanism to non-homogenous nonlinear fractional partial differential equations for both Caputo and Riemann-Liouville types derivatives in section 3. Implementation of the HDM to the Bergman model is presented in section 4. In section 5, we present the numerical simulation results, and the treatment and resolution of the Bergman model special case is and discussed.
For longer than five decades, fractional calculus proved to be a major player in modeling and analyzing linear and complex phenomena in engineering and the applied sciences. Extending the tools of its classical counterpart, non-integer type model equations and systems, most often describing nonlinear processes, are frequently treated and solved with the advent of what came to be known as fractional calculus. In recent years, fractional calculus started playing an even more essential role in various fields such as biology, biomedical engineering, geophysics, electricity, fluid dynamics, and mechanics [12,13,18,22]. Among its major contexts are Brownian motion, random walks and stochastic processes, control dynamics, fractional power law, Riesz potentials, fractals, nonlocal phenomena and porous media. Methods concentration span fractional type of computational derivative equations and systems, variational principles, boundary value problems, transform theory applications. Related studies scopes include, but are certainly not limited to, acoustic dissipation, chaos dynamics, control theory, image and signal processing, materials relaxation and creep, heat conduction, special functions, singularities analysis and integral representations, as well as viscoelasticity [23,29-36,37-42].
A vast literature exists presenting and discussing on various definitions advantages and disadvantages (see [33,43,44]). The most commonly fractional derivatives invoked in the literature to date are the Riemann-Liouville, and the Caputo derivatives.
While, the Caputo derivative is given by,
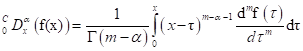 , (2.1)
, (2.1)
the Riemann-Liouville, is given by,
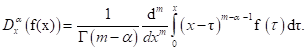 (2.2)
(2.2)
Although, the Caputo derivative of a constant is zero, it demands higher conditions of regularity for differentiability than the Riemann-Liouville derivative, for which, and in contrast, the fractional derivative of a constant is not zero. We need to calculate a function first derivative a priori to determine the fractional derivative in the Caputo sense. Consequently, the Caputo derivatives can be defined only for differentiable functions. On the other hand, functions with no first-order derivative may have fractional derivatives of all orders less than one, in the Riemann-Liouville sense. In 2006, Guy Jumarie proposed an alternative definition to the Riemann-Liouville derivative, [43],(see also 44] and refs therein),
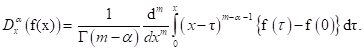 (2.3)
(2.3)
2021 Copyright OAT. All rights reserv
The modified Riemann-Liouville derivative contains advantages over both the Riemann-Liouville, and the Caputo fractional derivatives. Being defined for arbitrary continuous, even non-differentiable ones, the Jumarie fractional derivative of a constant turns out to be zero.
Definition 1 .A real function 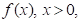 is said to be in the space
is said to be in the space 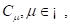 if there exists a real number
if there exists a real number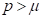 , such that
, such that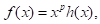 where
where 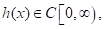 and it is said to be in the space
and it is said to be in the space 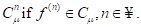
Definition 2. The Riemann–Liouville fractional integral operator of order,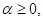 of a function,
of a function,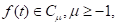 is defined through implementation of the integration operator,
is defined through implementation of the integration operator,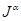 , in the following manner:
, in the following manner:
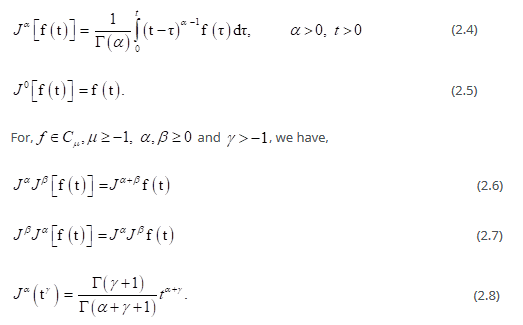
More relevant detailed properties of the operator J can be found in [43].
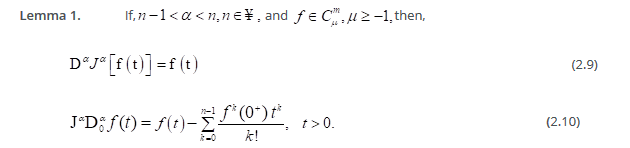
Definition3. Consider the 𝑛- variables, , function𝑓(x),of class
, function𝑓(x),of class We define the partial derivative of fractional order 𝛼, for 𝑓 with respect to 𝑥𝑖 by,
We define the partial derivative of fractional order 𝛼, for 𝑓 with respect to 𝑥𝑖 by,
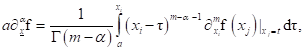 (2.11)
(2.11)
where, 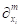 is the usual partial derivative of integer-order 𝑚.
is the usual partial derivative of integer-order 𝑚.
To illustrate the basic idea of HDM by considering a general fractional nonlinear, non-homogeneous partial differential equation, with the initial condition,
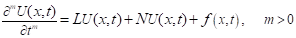 , (3.1)
, (3.1)
with respect to the initial conditions,
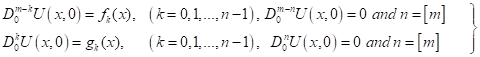 (3.2)
(3.2)
where, 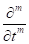 denotes the Caputo or Riemann-Liouville fraction derivative operator, L is the linear fractional differential operator, 𝑁 represents the general nonlinear fractional differential operator and
denotes the Caputo or Riemann-Liouville fraction derivative operator, L is the linear fractional differential operator, 𝑁 represents the general nonlinear fractional differential operator and 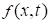 , is a known function.
, is a known function.
On taking the inverse operator, 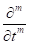 , on both sides of eqn. (3.1),in the case of the Riemann-Liouville fractional derivative,
, on both sides of eqn. (3.1),in the case of the Riemann-Liouville fractional derivative,

and the nonlinear term can be decomposed as,

Relating the terms of same powers of 𝑝, this gives solutions of various orders. The initial guess of the approximation is, G(𝑥,𝑡), is actually the Taylor series of the exact solution of order 𝑚. Uniqueness of the series decompositions is insured by this initial guess [23,40,45].
In this section we apply the steps of the HDM developed above to solving the system of fractional differential equations defined by,
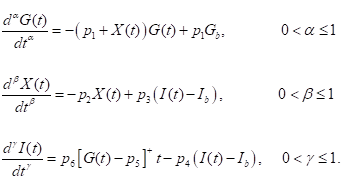
On using the HDM steps, we arrive at the following equations,
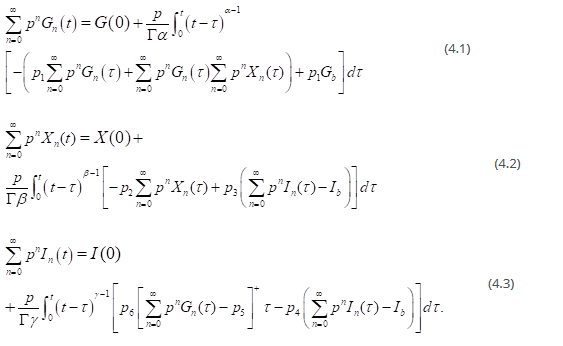
Comparing the coefficients of the same power of p, we get the following integral equations,
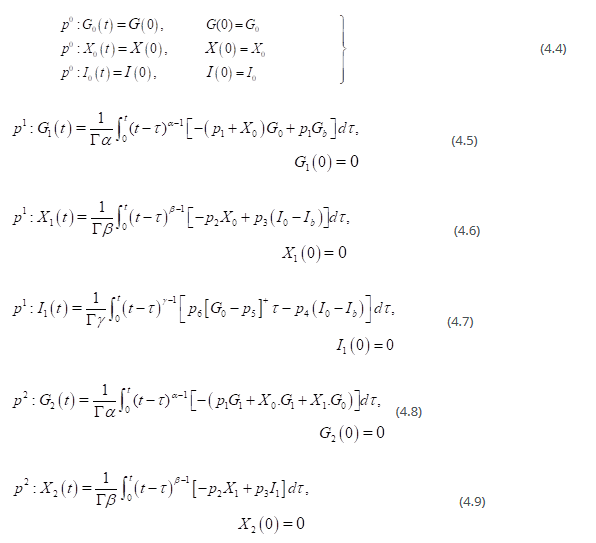
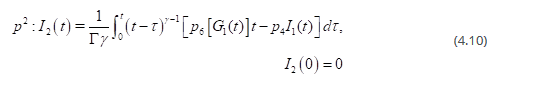
as well as
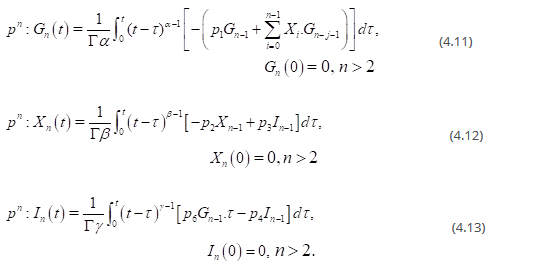
As a particular instance to be treated, we assume the base level blood glucose concentration to be, Gb= 92mg/dL, while the base level blood concentration of insulin to be say, Ib=7.3 mU/L. The glucose clearance rate to be independent of insulin p1= 0.03082 min-1, the rate of clearance of active insulin (decrease of uptake), p2= 0.02093 min-1, the increase in uptake ability caused by insulin, p3 = 1.062 x 10-5 L/(min2mU), the decay rate of blood insulin to be, p4 = 0.3 min-1, the target glucose level, p5 = 89.5 mg/dL, and the rate of pancreatic release after glucose bolus is, p6 = 0.3349 x 10-2 mUdL/Lmgmin.
The components of the series solution are obtained directly
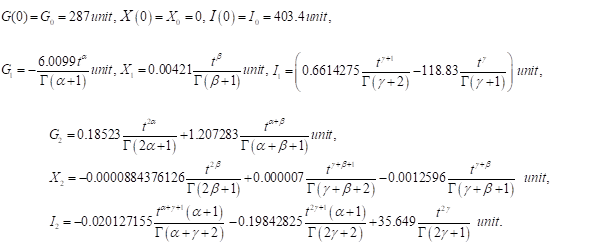
The remaining terms can be obtained in the similar manner.
Here we consider, only few terms of the series solutions, and the asymptotic solution is,

If we take,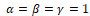 , inequation (3.1),the Minimal model becomes,
, inequation (3.1),the Minimal model becomes,
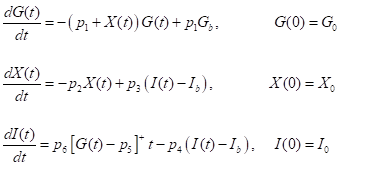
which upon solving, yields the following approximate solutions to our problem,
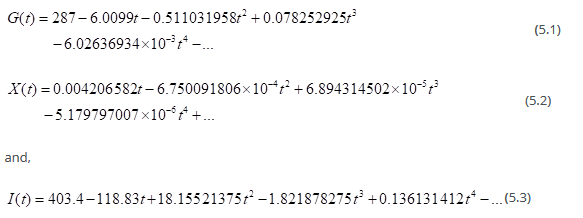
Only the fourth-order term of the series, of the above said methods was used in evaluating the approximate solutions. The accuracy of our approximate solutions can be improved by computing more terms of the approximate solutions.
Graphical representation of (5.1), (5.2), and (5.3)
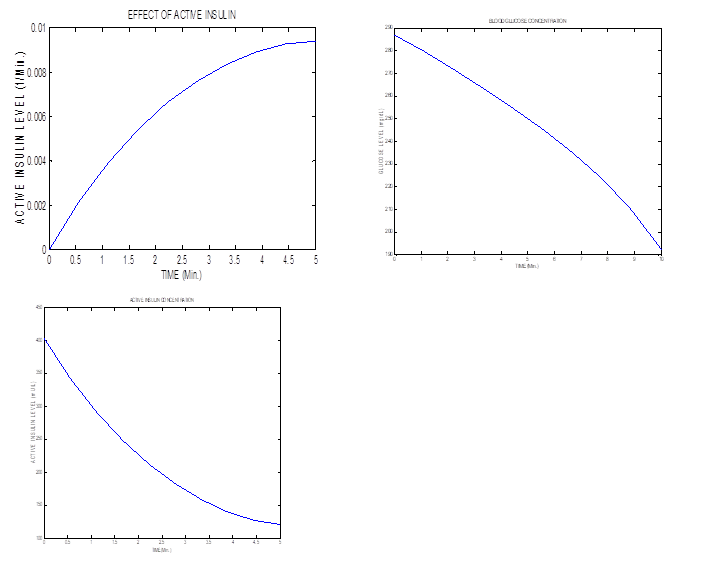
Numerical solutions in our study cases investigated seem to represent the biological behavior of real life situations. The approximate solutions of the fractional order are increasing continuous functions of the fractional order derivatives. Both systems of nonlinear equations were solved via an iteratively direct technique, namely, the HDM. The basic characters of the relatively highly versatile technique were presented in detail. As a means for solving the illustrated problems above, and various other problems of engineering and physical sciences processes, the HDM turns out to be straightforward, economic in time consumption, on top of being user-friendly [19,20,23,37-42,44,46,47]. We propose to use it in future works with classical or fractionally modeled diabetic retino-graphy stages, or mast cells growth based multiple sclerosis cure [48,49]. Furthermore, while standard Tuberculosis models development can be for instance found in [50,51], the models presented above, cover both integer and non-integer-order derivatives. A follow-up study shall focus on comparisons such works and ramifications, as non-factional orders tend to integer ones in the limit, and possibly vice versa. We call on interested readers and researchers to join this planned task.
Fethi Bin Muhammad Belgacem is pleased to acknowledge the continued support of the Kuwait Public Authority for Applied Education and Training Research Department, (PAAET RSD).
- Eckstein EC, Belgacem F (1991) Model of platelet transport in flowing blood with drift and diffusion terms, extended platelet transport equation, Biophys J 60: 53-69. [Crossref]
- Belgacem FBM (1997) Elliptic boundary value problems with indefinite weights: Variational formulations of the principal eigenvalue and applications, Pitman Research Notes Series, 368, Addison-Wesley-Longman, New York, USA.
- Mountrakis L, Lorenz E, Hoekstra AG (2013) Where do the platelets go? A simulation study of fully resolved blood flow through aneurysmal vessels. Interface Focus 3: 20120089. [Crossref]
- Bourouiba L, Dehandschoewercker E, Bush JWM (2014) Violent expiratory events: on coughing and sneezing. J Fluid Mech 745: 537-563.
- Belgacem FBM, Cosner C (1995) The effects of dispersal along environmental gradients on the dynamics of populations in heterogeneous environments. Canadian Applied Mathematics Quarterly 3: 379–397.
- Belgacem FBM (1999) Theory and application with weight indefinite elliptic boundary value problems. International Journal on Problems of Nonlinear Analysis in Engineering Systems 5: 51-58.
- Belgacem FBM (2001) Diffusion and drift models for population dispersal from stochastic and continuum views. International Journal of Applied Mathematics 5: 85-106.
- Belgacem FBM, Smaoui N (2001) Interactions of parabolic convective diffusion equations and Navier-Stokes equations connected withpopulation dispersal. Communications on Applied Nonlinear Analysis 8: 47-67.
- Smaoui N, Belgacem FBM (2002) Connections between the convective diffusion equation and the forced burgers equation. Journal of Applied Mathematics and Stochastic Analysis 15: 53-69.
- Belgacem FBM (2009) Triple modeling scheme for optimal control related to weighted population dispersal, Nonlinear Studies 16: 371-380.
- Katatbeh QD, Belgacem FBM (2011) Applications of the Sumudu transform to fractional differential equations. Nonlinear Studies 18: 99-112.
- Chaurasia VBL, Dubey RS, Belgacem FBM (2012) Fractional radial diffusion equation analytical solution via Hankel and Sumudu transforms. Mathematics in Engineering, Science and Aerospace 3: 1-10.
- Dubey RS, Goswami P, Belgacem FBM (2014) Generalized time-fractional telegraph equation analytical solution by Sumudu and Fourier transforms. Journal of Fractional Calculus and Applications 5: 52-58.
- Goswami P, Belgacem FBM (2012) Fractional differential equations solutions through a Sumudu rational. Nonlinear Studies Journal 19: 591-598.
- Gupta VG, Sharma B, Belgacem FBM (2011) On the solutions of generalized fractional kinetic equations. Applied Mathematical Sciences 5: 899 – 910.
- Bulut H, Baskonus HM, Belgacem FBM (2013) The analytical solution of some fractional ordinary differential equations by the Sumudu transform method. Abstract and Applied Analysis.
- Javidi M, Nyamoradi N (2013) Numerical behavior of a fractional order HIV/AIDS epidemic model. World Journal of Modelling and Simulation 9: 139-149.
- Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations, Wiley, New York, 1993.
- Bulut H, Baskonus HM, Tuluce DS (2012) Homotopy perturbation Sumudu transform method for one and two dimensional homogeneous heat equations. International Journal of Basic & Applied Sciences 12: 6-16.
- Bulut H, Baskonus HM, Tuluce DS (2013) Homotopy perturbation Sumudu transform method for heat equations. Mathematics in Engineering, Science and Aerospace 4: 49-60.
- Atangana A, Kiliçman A (2013) Analytical solutions of boundary values problem of 2D and 3D poisson and biharmonic equations by homotopy decomposition method. Abstract and Applied Analysis.
- Atangana A, Kiliçman A (2013) A possible generalization of acoustic wave equation using the concept of perturbed derivative order. Mathematical Problems in Engineering.
- Touchent KA, Belgacem FBM (2015) Nonlinear fractional partial differential equations systems solutions through a hybrid homotopy perturbation Sumudu transform method. Nonlinear Studies 22: 591-600.
- Caumo A, Cobelli C, Omenetto M (1999) Overestimation of minimal model glucose effectiveness in presence of insulin response is due to under modeling. Am J Physiol 278: 481-488.
- De Gaetano A, Arino O (2000) Mathematical modelling of the intravenous glucose tolerance test. J Math Biol 40: 136-168. [CrossRef]
- Gatewood LC, Ackerman E, Rosevear JW, Molnar GD, Burns TW (1968) Tests of a mathematical model of the blood-glucose regulatory system. Comput Biomed Res 2: 1-14. [Crossref]
- Bergman RN, Ider YZ, Bowden CR, Cobelli C (1979) Quantitative estimation of insulin sensitivity. Am J Physiol 236: 667- 677.
- Bowden CR, Bergman RN, Toffolo G, Cobelli C(1980) Minimal modeling, partition analysis, and identification of glucose disposal in animals and man. IEEE Transactions on Biomedical engineering 129–135.
- Atangana A, Alabaraoye E (2013) Solving a system of fractional partial differential equations arising in the model of HIV infection of CD4+ cells and attractor one-dimensional Keller-Segel equations. Adv in Difference Equations.
- Atangana A, Botha JF (2012) Analytical solution of the groundwater flow equation obtained via homotopy decomposition method. Journal of Earth Science & Climatic Change 3: 1-4.
- Kilbas A, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations, Elsevier, Amsterdam.
- Baleanu D, Diethelm K, Scalas E, Trujillo JJ (2012) Fractional Calculus, Series on Complexity, Nonlinearity and Chaos, World Scientific, Models & Numerical methods.
- Podlubny I (1999) Fractional differential equations, Academic Press, NewYork, USA, 1999.
- Caputo M (1967) Linear models of dissipation whose Q is almost frequency independent, part II. Geophysics Journal Int 13: 529-539.
- Chaurasia VBL, Dubey RS (2011) Analytical solution for the differential equation containing generalized fractional derivative operators and Mittag-Leffler-type function, International Scholarly Research Network. ISRN Applied Mathematics.
- Chaurasia VBL, Dubey RS (2013) Analytical solution for the generalized time fractional telegraph equation. Fractional Differential Calculus 3: 21–29.
- Tuluce DS, Bulut HH, Belgacem FBM (2014) Sumudu transform method for analytical solutions of fractional type ordinary differential equations. Mathematical Problems in Eng., Special Issue: Partial Fractional Equations and their Applications, 1-6.
- Baskonus HM, Belgacem FBM, Bulut H (2015) Solutions of nonlinear fractional differential equations systems through the implementation of the variational iteration method. De Gruyter Open "Fractional Dynamics" Book, Ch.19: 343-353.
- Mekkaoui T, Hammouch Z, Belgacem FBM, Al-Abbasi A (2015) Fractional order nonlinear systems: chaotic dynamics, numerical simulations and circuits designs. De Gruyter Open "Fractional Dynamics" Book, Ch.19: 354-368.
- Belgacem FBM, Gulati V, Goswami P, Aljouiee A (2015) On generalized fractional differential equations solutions: Sumudu transform solutions and applications, De Gruyter Open "Fractional Dynamics" Book, Ch.22, 382-393.
- Jumarie G (2006) Modified Riemann-Liouville derivatives and fractional Taylor series of nondifferentialble functions further results. Computers and Mathematics with Applications 51: 1367-1376.
- Belgacem FBM, Sivasundaram S (2015) New computational techniques and transform theory applications to nonlinear fractional and stochastic differential equations and systems. Nonlinear Studies 22: 561-563.
- Jumarie G (2005) On the representation of fractional Brownian motion as an integral with respect to (dt). Applied Mathematics Letters 18: 739-748.
- Acharya UR, Lim CM, Ng EYK, Chee C, Tamura T (2009) Computer-based detection of diabetes retino-graphy stages using digital fundus images. Proc Inst Mech Eng Part H: J. Engineering in Medicine 223: 545-553.
- Ghorbani A (2009) Beyond Adomian’s polynomials He’s polynomials. Chaos Solitons and Fractals 39: 1486–1492.
- Dubey RS, Alkahtani BST, Atangana A (2014) Analytical solution of space-time fractional Fokker-Plank equation by homotopy perturbation Sumudu transform method. Mathematical Problems in Engineering.
- Abbaoui K, Cherruault Y (1995) New ideas for proving convergence of decomposition methods. Computers and Mathematics with Applications 29: 103–108.
- Bulut H, Baskonus HM, Tuluce S (2012) Homotopy perturbation sumudu transform method for one-two-three-dimensional initial value problems. e-Journal of New World Sciences Academy 7: 55-65.
- Krüger PG (2014) Mast Cells: the key to multiple sclerosis?. World Journal of Neuroscience 4: 120-124.
- Aparicio JP, Castillo-Chavez C (2009) Mathematical modelling of Tuberculosis epidemics. Mathematical Biosciences and Engineering 6: 209-237.
- Trauer JM, Denholm JT, McBryde ES (2014) Construction of a mathematical model for tuberculosis transmission in highly endemic regions of the Asia-pacific. J Theor Biol 358: 74-84. [Crossref]

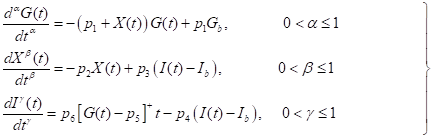 (1.1)
(1.1)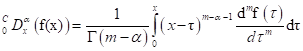 , (2.1)
, (2.1)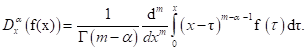 (2.2)
(2.2)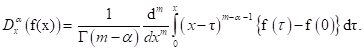 (2.3)
(2.3)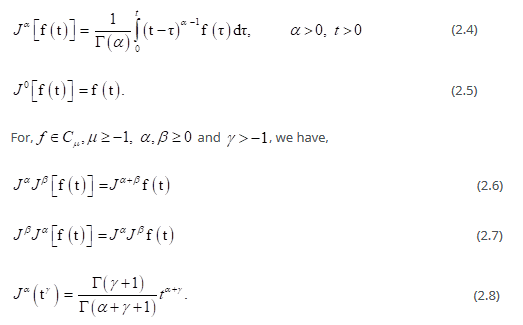
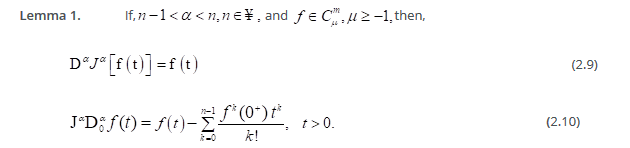
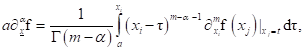 (2.11)
(2.11)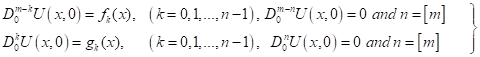 (3.2)
(3.2)