Investigation of state and equal-intrinsic energy curved surfaces of the ideal gas using analytic geometrical method generated intrinsic energy equation,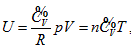 , continued equality, covering all the basic theories of ideal gas.
, continued equality, covering all the basic theories of ideal gas.
- Ideal gas state curved surface, PV = nRT, is a ruled quadric surface. The curved surface equation of a state is
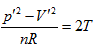
- Twelve differential equations were obtained through theoretical derivation from various respects
- Curved surface equation of intrinsic energy
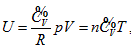 , the continued equality, derived herein includes all the basic theories of ideal gas
, the continued equality, derived herein includes all the basic theories of ideal gas
Joule’s law has both verifiability and falsifiability. It includes four of the twelve partial differential equations derived from continued equality, but excludes the rest eight
In the free expansion experiment, Gay-Lussac and Joule proved that both gas pressure and volume changed before and after the vacuum expansion while temperature and intrinsic energy are kept unchanged. Thus, Joule’s Law concluded that “the intrinsic energy of the ideal gas was only correlated with temperature of the system, while independent of its pressure and volume” [1]. Even though Joule’s free expansion experiment was not necessarily the most accurate, it significantly impacted the development of modern thermodynamics theory gaining unanimous recognition. Thereafter, tremendous amount of research was done to improve Joule law.
Up to the late 20th century, people just began to change their opinions about free expansion. Klotz and Rosenberg in 1972 [2] argued that temperature during the free expansion process was not a definite value, and it restored automatically after the system rebalanced. In 1989, Xiancai Fu and co-workers [1] described that the temperature remained unchanged during the free expansion process because of the large heat capacity of water, thus the temperature change could not be measured, therefore, the conclusion could be correct under the condition of P→0. Around 1997, while debating with James J. Robinson, A. G. Guy [3,4] derived U = 3/2 PV [5], which illustrated that the internal energy U is the composite function of both P and V instead of only T. In 1997, Yan and Gao [6] also did further free expansion studies in this regard resulting in the same conclusion. Liu and co-workers [7] then verified the same conclusion from the quantum statistical physics point of view in 2000. In 1998, Zhao and Luo [8] explicitly stated in their book Thermotics that “the intrinsic energy of ideal gas is not related with volume”, concluded from the experiment conducted by both Gay Lussac and Joule, cannot be considered as the final conclusion. The authors further stated that the Joule law relied on the experiment performed by Rossini–Frandsen [9] in 1932.
It is clear that the classical free expansion, Joule’s law, and the concept of ideal gas fell into crisis under such a situation. First, free expansion got into the following dilemma: if ‘the temperature varies in the free expansion process’ is accepted, it would then be a counter example to Joule’s law; If it was approved that the temperature of “ideal gas” in thermodynamics could change before and after free expansion, then it could be hard to distinguish “ideal gas” and non-deal gas because the free expansion system belongs to non-deal gas in the statistic physics when pressure P >> 0 in the classical free expansion system. If one insisted that the temperature remained unchanged before and after free expansion, namely, the temperature of “non-ideal gas” in statistical physics didn’t change before and after free expansion, and then it could not be distinguished from the “ideal gas”. Secondly, Joule’s law faces the following challenge: theoretically, when ideal gaseous equation is utilized in the composite function in molecular kinetic theory and mathematics, the intrinsic energy of the deal gas system is still the function of P and V. On the experiment basis, Joule’s law depends on the success of Rossini–Frandsen’s experiment after losing support from free expansion [9]. Washburn once revised and developed the bomb calorimetry based on this experiment. However, the fundamental base for this experiment was that “the intrinsic energy and pressure of gas system are in a linear relationship”, namely, U (P, T) = f (T) P + g (T). When this linear relationship is extrapolated to P → 0, one can only say U → g (T). However, if thus reached the conclusion that “the intrinsic energy had no relationship with pressure”, it would be obviously contradictory with the premise that “the intrinsic energy and pressure of gas system are in a linear relationship”. P→0 was only a value used, instead of omitting the influence of pressure on intrinsic energy. Unless the statement “as the pressure changes, the data of each experimental point near P→0 forms divergent sequence around intrinsic energy axile” stands, the Joule law couldn’t be supported.
The trend for the theoretical exploration in the field would certainly deprive the experimental base of Joule’s law. The real key here is that Joule’s law and the first law of thermodynamics are incompatible. The first law clearly determines that “the intrinsic energy is the univalent function of states”, while the Joule's law determines the intrinsic energy of a system only relying on temperature property even under the circumstance of the undetermined system state. The properties of pressure and volume could be used to determine the state of an enclosed system while Joule law claimed that they have nothing to do with the intrinsic energy. The equation U = 3/2 PV derived by A. G. Guy [4] was the conclusion of statistical physical axiom, but it could not be used as the final argument for the thermodynamic axiom.
We reported in 2011 [10] that the internal energy of an ideal-gas can not only be expressed as the product of its volume and pressure but can also be expressed as the product of its temperature and quantity of gas. Therefore, the statement of “the internal energy of an ideal gas is independent of its pressure and volume” is an inaccurate statement. In 2014, Stepanov [11] described the ideal gas paradox and declared that it was the wrong approach to express the internal energy of a simple gas as the only function of temperature. Instead, multivariable equations of state derived from composite functions must be used. In 2016, we [12] reported the studies on the relationship between internal energy and state of ideal gas in which the Continued Equality, depicted as “The internal energy of the ideal gas has interrelationship with each state function”, was derived for the first time.
The historical contributions of Joule’s law and its contradictions in thermodynamics indicated that it should have both verifiability and falsifiability in theory [10]. In this paper, we describe the curved surfaces of both state and equal-intrinsic energy of ideal gas on the basis of the static and homogeneous states by utilizing analytic geometrical method and by following the first law of thermodynamics. We explored and determined the method to solve the problems and contradictions mentioned above. The continued equality was derived and further experimentally verified [13].
In thermodynamic theory system, the so-called “ideal gas” refers to the relationship among all the system state properties that has to be consistent with the laws of Boyle, Gay-Lussac, and Charles. In the 19th century, people merged them as the following ideal gas equation:
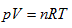
“The ideal gas” in statistical physics is the gas formed by a group of constantly moving and non-potential mechanical particles. With the method dealing with the close independent subsystem, it can be obtained: 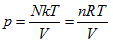
Therefore, in the classical theory arena, studies of ideal gas equation meet the common requirements of the above two theory systems.
According to the extensive property of intrinsic energy, it can be explained that gas volume is also the essential variable to determine intrinsic energy. Therefore, the ideal gas equation, obtained from both thermodynamics and statistical physics perspectives, should be a function equation formed by four properties P, V, n, T. Because the state equation obtained is a quadratic function, thus it could be assumed that its standard form is a quaternary quadratic equation:
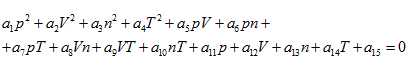
The ideal gas equation obtained above is the result when a5 = 1, a10 = -R, and all of the rest coefficients are zero. Under the condition of 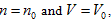 the ideal gas equation could be expressed as the form of Charles law:
the ideal gas equation could be expressed as the form of Charles law: 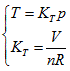 ,
,
it means, in P∼ V∼T coordinates, all the possible corresponding points for temperature and pressure values could be interconnected to a straight line, and its linear slope is 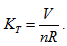 . The closed systems with the same gas volume could have different slopes because of different volumes; therefore, all the straight lines may not coexist in the same plane. Because V could value continuously within the interval of
. The closed systems with the same gas volume could have different slopes because of different volumes; therefore, all the straight lines may not coexist in the same plane. Because V could value continuously within the interval of 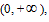 thus all P ∼ V straight lines could be interconnected to a curved surface. Under the condition of
thus all P ∼ V straight lines could be interconnected to a curved surface. Under the condition of 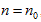 , each state point determined by P, V and T would definitely be passed through by certain straight line determined by
, each state point determined by P, V and T would definitely be passed through by certain straight line determined by 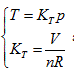 and is passed through by only one single straight line. Thus, it can be determined that the state curved surface of a closed ideal gas system is a ruled quadric surface. Similarly, the same result can also be obtained from Gay Lussac law, expressed as:
and is passed through by only one single straight line. Thus, it can be determined that the state curved surface of a closed ideal gas system is a ruled quadric surface. Similarly, the same result can also be obtained from Gay Lussac law, expressed as: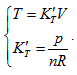 Therefore, the state surface has two groups of straight generatrixes (see Figure 1).
Therefore, the state surface has two groups of straight generatrixes (see Figure 1).
The curved surface shown in Figure 1 has one symmetric plane p = V. The intersecting line of state curved surface and symmetric plane is: 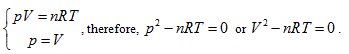
Here is the parabola equation which gives the OA line in Figure 1. Moreover, it is also perpendicular to the symmetric plane and parallel to the plane of axis T; then, the intersecting line between p =-V + c and the state curved surface is:
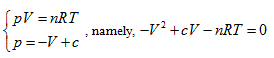
This is also a parabola equation which gives a line with opposite direction, such as Line BC in Figure 1. Therefore, the state curved surface of ideal gas may be a hyperbolic paraboloid. It can be verified as follows:
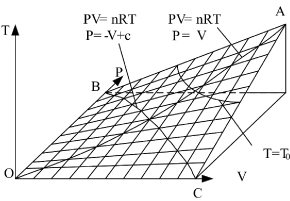
Figure 1. State curved surface of the sealed ideal gas system in P, V, T three-dimensional space

Figure 2. State curved surface and equal-intrinsic energy of enclosed ideal gases in P, V, T three-dimensional space
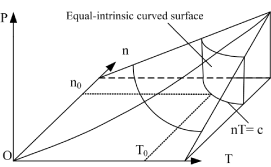
Figure 3. Curved surface of both state and equal internal energy for ideal gases with open and constant volume in P, V, T three-dimensional space
Rotating the p ∼ V ∼ T coordinate system 45° horizontally around the Axis T, the substitution equation of the coordinates is:
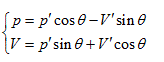
Substituting them into the ideal gas equation gives:
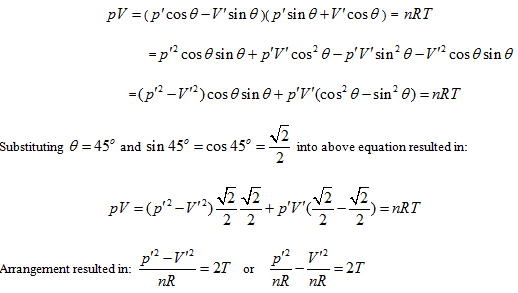
This is the standard equation of hyperbolic paraboloid with a shape of saddle. This surface has two groups of straight generatrixes, having the following equations:
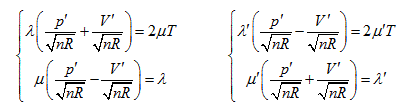
Substitute the coordinate transformation equations 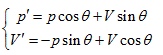
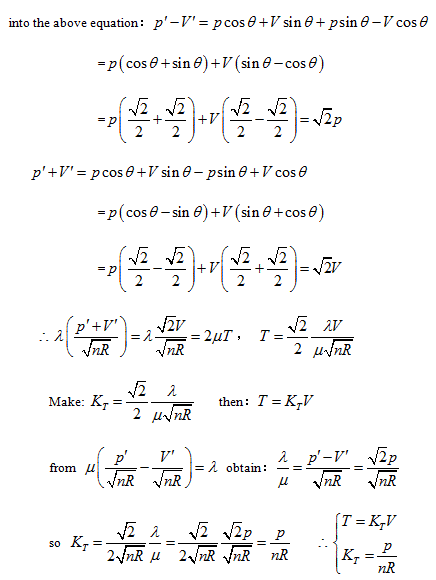
This result is exactly the form of Gay Lussac’s law and also the intersecting line of isobaric plane and state curved surface.
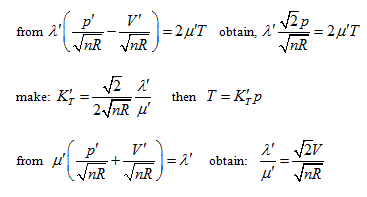
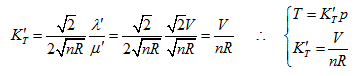
This is the form of Charles’ law, and also the intersection equation of isosteric plane and state curved surface.
The intersection standard equation of state curved surface and isothermal plane can be expressed as:
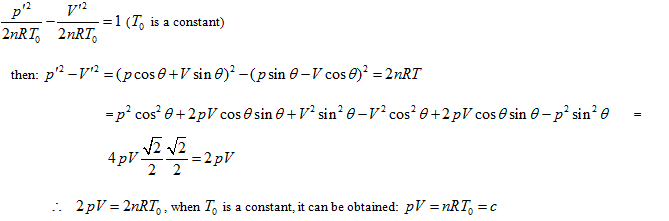
This is the mathematical form of Boyle law and also the intersection equation of isothermal plane and state curved surface.
In P∼V∼T coordinate system, the role of the fourth variable n is, when the product of p and V is fixed, the greater the volume of gas content , the lower the corresponding temperature. The position of the state curved surface is also relatively low. Therefore, the geometry space expressed by ideal gas equation is a family of curved surfaces which are overlapping and mutually intersecting with axes P and V.
According to the physical significance of system property, domain of definition of p, V, n, T can continuously value within the interval 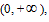 So the family of curved surfaces should fill the first octant of three-dimensional space.
So the family of curved surfaces should fill the first octant of three-dimensional space.
According to the point of view that "intrinsic energy is the univalent function of state", when the property coordinate system of ideal gas determines the state of the system, it also inevitably determines the intrinsic energy of the system. For general cases, when the gas volume is variable, the system state requires at least three properties to be determined. Different combinations correspond to four 3-dimensional coordinates:
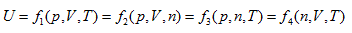
The coordinate system P ∼ V ∼ Tis considered as an example for further analysis (see below).

Herein, 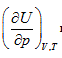 requires
requires 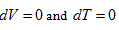 . This is the rate of intrinsic energy change with pressure in the open isosteric system with constant temperature. The open isosteric system means the artificially specified space of a research system. The specified space is considered as the research system, and the outside of this space is the environment. The exchange of substance and energy can be realized between the system and environment. With the consideration of the influence of “heat convection” in the open system, the amount of heat exchange of an open system should be the function of gas amount and temperature of the system, according to the definition of heat capacity:
. This is the rate of intrinsic energy change with pressure in the open isosteric system with constant temperature. The open isosteric system means the artificially specified space of a research system. The specified space is considered as the research system, and the outside of this space is the environment. The exchange of substance and energy can be realized between the system and environment. With the consideration of the influence of “heat convection” in the open system, the amount of heat exchange of an open system should be the function of gas amount and temperature of the system, according to the definition of heat capacity:
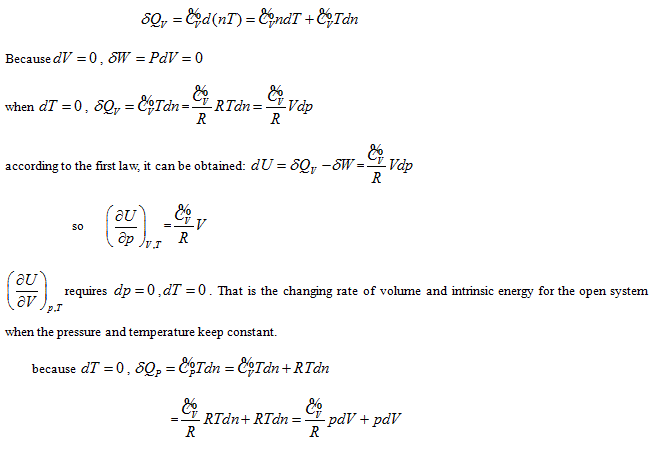
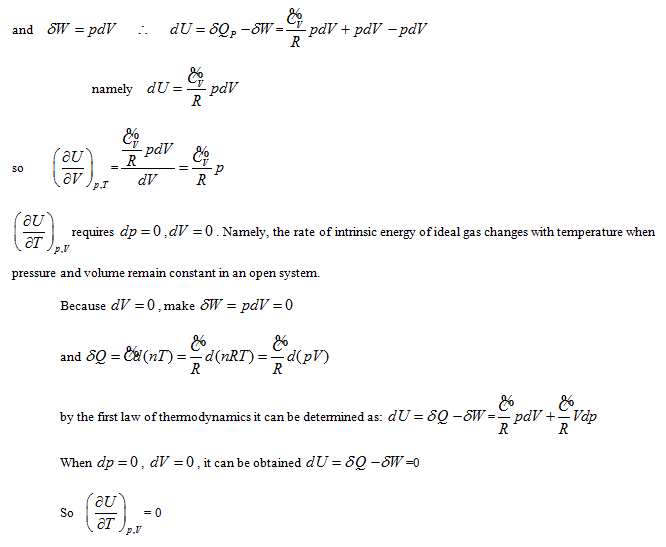
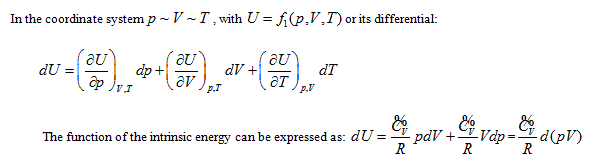
The above derivation can be analyzed as the following:
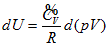 illustrates that the intrinsic energy of the system can be determined by the product of pressure and volume in the coordinate system p∼V∼T. The intrinsic energy of the system varies with the rectangular planar area within the plane p∼V surrounded by the four straight lines axis P and V as well as
illustrates that the intrinsic energy of the system can be determined by the product of pressure and volume in the coordinate system p∼V∼T. The intrinsic energy of the system varies with the rectangular planar area within the plane p∼V surrounded by the four straight lines axis P and V as well as 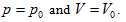
When the system state is determined, there is only one intrinsic energy value. However, after the intrinsic energy is determined, there may be many corresponding system states. All corresponding points for the p and V values of the possible states within the plane p∼V are interconnected into an inverse curve: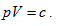
In coordinate system p∼V∼T, with the continuous change of gas volume, this curve can be developed into a curved surface parallel to the axis T. This is the equal-intrinsic energy surface for 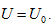 . The surface generatrix is
. The surface generatrix is 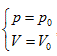 , namely, the geometric significance of
, namely, the geometric significance of 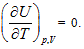 The intersecting line of the equal-intrinsic energy surface and the state curved surface
The intersecting line of the equal-intrinsic energy surface and the state curved surface 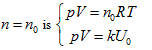
obtained: 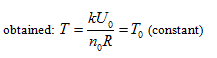
in the above equation, Uo stands for the equal-intrinsic energy surface, no is the state curved surface of certain enclosed system, and Tois the isothermal surface. According to current thermodynamic method, if the system always remains as the uniform state during the process, when the intrinsic energy and temperature keep constant in the free expansion process, the pressure and volume of this system can only change along with the common intersecting line of “the equal-intrinsic energy surface”, “isothermal surface”, and “the state surface of enclosed system”.
By utilizing the same method mentioned above to analyze the coordinate system p ∼ V ∼ n, similar result can also be obtained:
In the coordinates p ∼ V ∼ n, equal-intrinsic energy can be expressed as: 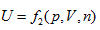 . It can be differentiated as:
. It can be differentiated as:
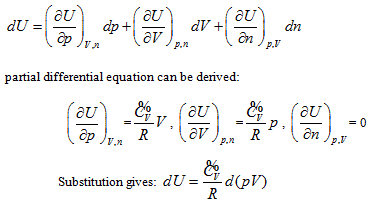
The result is the same as that obtained from the coordinate system p ∼ V ∼ T. The geometrical pattern and analyzing methods used are all the same as those in the coordinate system p ∼ V ∼ n except the axis T of the coordinate system is changed into axis n.
2021 Copyright OAT. All rights reserv
In the coordinate system p ∼ V ∼ n, intrinsic energy can be expressed as 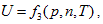 , and it is differentiated as:
, and it is differentiated as:
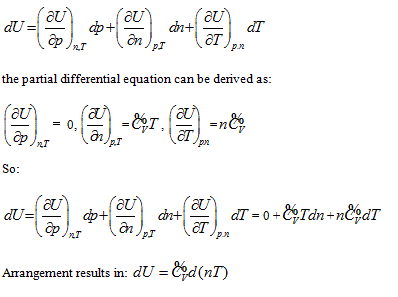
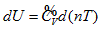 means that the system intrinsic energy can be determined by the product of gas volume and temperature in the coordinate system p ∼ n ∼ T. The intrinsic energy value of the system is proportional to the area of the rectangle formed by axis n, axis T, n = no, and T = Tofour straight lines in the n ∼ T plane.
means that the system intrinsic energy can be determined by the product of gas volume and temperature in the coordinate system p ∼ n ∼ T. The intrinsic energy value of the system is proportional to the area of the rectangle formed by axis n, axis T, n = no, and T = Tofour straight lines in the n ∼ T plane.
In coordinate system n ∼ V ∼ T, intrinsic energy can be expressed as  . It is differentiated as:
. It is differentiated as:

This result is consistent with that of coordinate system p ∼ n ∼ T, and the corresponding graphics and analysis method are also similar.
Combination of all expressions for the system intrinsic energy of an ideal gas within the four coordinate systems mentioned above results in the following continued equality:
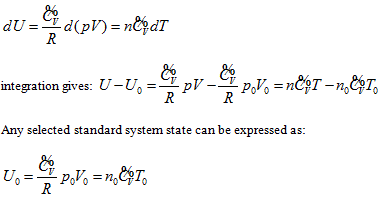
So, the function relationship between the intrinsic energy and state of the system can be expressed as:
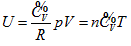
This equation can be utilized to determine the intrinsic energy of any ideal gas system when the common reference standard was set based on the base point, such as 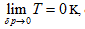 , of the coordination system.
, of the coordination system.
Analysis of verifiability and falsifiability of Joule Law
The verifiability of Joule’s law is that it determines a measure method of system intrinsic energy, while its falsifiability is its exclusion for other measure methods for intrinsic energy. Using the twelve partial differential equations for the intrinsic energy measurement derived by the analytic geometrical method described above, one can determine the uniform measurement of the intrinsic energy for any system, including different quality system. Through careful one-by-one comparison, one can conclude that Joule law statements “intrinsic energy only has relationship with system temperature” includes the following four partial differential equations in the closed system:
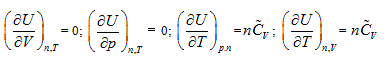
However, considering Joule’s statement “system intrinsic energy has nothing to do with pressure and volume”, along with the relationship between intrinsic energy and gas volume, Joule’s law excludes the rest of eight partial differential results as shown below:
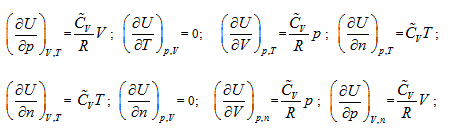
Because Joule law’s statement includes four of these equations, the difference of intrinsic energy in closed system before and after the state change can be determined based on Joule law. The exclusion of the other eight equations by Joule’s law leads to its incompatibility with the first law of thermodynamics. In all the twelve partial differentials, four partial differentials indicate Joule’s law’s verifiability, while eight partial differentials show its falsifiability, which also embodies the complementation of verifiability and falsifiability.
Free expansion experiment
The origin of the dilemma, as to whether the temperature changes before and after free expansion, is the difference between “ideal gas concept” in the definition of “mathematical limit” in statistical physics and the definition of “measuring distinguishability” in thermodynamics. Joule’s law gives the “privilege” that ideal gas temperature property is the only related factor with intrinsic energy, which dictates whether the temperature changes before and after free expansion becoming the only factor to define an ideal gas. In analyzing this core dilemma, the continued equality clearly proved the verifiability and falsifiability of Joule’s law; free expansion was no longer the standard to distinguish the ideal and non-ideal gasses. The corresponding meaning then naturally turned into “when the change of molecular interactions is small enough to be ignored before and after the vacuum expansion, the temperature change can also be ignored”. Therefore, both challenges, the dilemma of free expansion and the relationship between intrinsic energy of ideal gas with temperature, are easily resolved. “Ideal gas” then naturally regressed as a theoretical model.
Connection of continued equality with the current theory
The continued equality obtained above by using analytic geometrical method based on the first law of thermodynamics can also be derived through thermodynamic method and statistical physics method, and it covers the classical gas three laws, polytropic process, and Joule’s law as well as all the basic theories of ideal gas in statistical physics. In addition, the derivation of Joule’s law by the second law of thermodynamics is essentially the results by introducing the inherent property of intrinsic energy 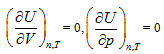 into Maxwell equation, and it has no direct relationship with the second law. Based on its containment of thermodynamics content and reasonable connection, the continued equality described herein is smoothly incorporated into the current theory system.
into Maxwell equation, and it has no direct relationship with the second law. Based on its containment of thermodynamics content and reasonable connection, the continued equality described herein is smoothly incorporated into the current theory system.
Ideal gas state curved surface, expressed by PV = nRT, is a ruled quadric surface in P ∼ V ∼ T three-dimensional space, and a hyperbolic paraboloid in the shape of saddle after horizontally rotating 45°. The curved surface equation of a state is 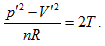 The equal intrinsic energy surface of ideal gas in three-dimensional property coordinates is perpendicular to P ∼ V plane or the inverse surface of the n ∼ T plane. Curved surface equation of intrinsic energy is
The equal intrinsic energy surface of ideal gas in three-dimensional property coordinates is perpendicular to P ∼ V plane or the inverse surface of the n ∼ T plane. Curved surface equation of intrinsic energy is 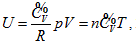 known as continued equality which includes all the basic theories of the ideal gas. Among the twelve partial differential equations derived from continued equality, Joule’s law only includes four of them, but excludes the rest eight, which indicates that Joule’s law has both verifiability and falsifiability. The detail experimental verification on the continued equality will be described in the subsequent article [13].
known as continued equality which includes all the basic theories of the ideal gas. Among the twelve partial differential equations derived from continued equality, Joule’s law only includes four of them, but excludes the rest eight, which indicates that Joule’s law has both verifiability and falsifiability. The detail experimental verification on the continued equality will be described in the subsequent article [13].
The authors thank Dr. Zhiyong Ren and Chihui An for valuable suggestions, comments and encouragement during the preparation of this manuscript and literature collection.
- Fu XC, Shen WX, Yao TY (1989) Physical Chemistry, Higher Education Press, Beijing.
- Klotz IM, Rosenberg RM (1972) Chemical Thermodynamics: Basic Theory and Methods, Third Edition, W. A. Benjamin, Inc., Menlo Park, California.
- Guy AG (1997) More on ideal gas. J Miner Met Mater Soc 49: 4-5.
- Stracher GB, Guy AG (1998) The internal energy of a PV = RT gas: a univariable or multivariable function, Math Geol 30: 251-258.
- Robinson JJ, Trumble KP, Gaskell DR (1997) More on the ideal gas law. J Miner Met Mater Soc 49: 3.
- Yan FL, Gao T (1997) Function forms of PV = 3U/2V, College Physics, 16: 21-22.
- Liu FZ, Wu YX, Han LY (2000) A relationship between internal energy and state of ideal gas. J Xuzhou Norm Univ (Nat. Sci. Ed.) 18: 38-40.
- Zhao KH, Luo WY (1998) Thermotics, Higher Education Press, Beijing.
- Rossini FD, Frandsen M (1932) The calorimetric determination of the intrinsic energy of gases as a function of the pressure. Data on oxygen and its mixtures with carbon dioxide to 40 atmospheres at 28°C. Bur Stand J Res 9: 733-747.
- Yao XW (2011) Mathematics relation between the state function and internal energy of the perfect gas. Henan Sci 29: 397-402.
- Stepanov I (2014) Explanation of an ideal gas paradox, Phys. Chem.: An Indian J 9: 151-152.
- An H, Yao XW, Yang GS, Hou JQ, Niu TS (2016) “Studies on the relationship between internal energy and state of ideal gas”, 251at ACS National Meeting, San Diego, CA, USA, March 13-17 PAPER No. PHYS-560.
- Yao XW, An H Experimental Validation of the Relationship between Internal Energy and State of Ideal Gas, This Journal, subsequent article.

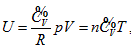 , continued equality, covering all the basic theories of ideal gas.
, continued equality, covering all the basic theories of ideal gas.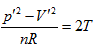
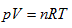
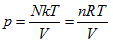
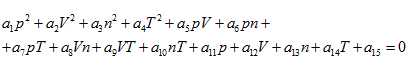
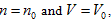 the ideal gas equation could be expressed as the form of Charles law:
the ideal gas equation could be expressed as the form of Charles law: 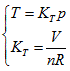 ,
, 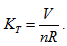 . The closed systems with the same gas volume could have different slopes because of different volumes; therefore, all the straight lines may not coexist in the same plane. Because V could value continuously within the interval of
. The closed systems with the same gas volume could have different slopes because of different volumes; therefore, all the straight lines may not coexist in the same plane. Because V could value continuously within the interval of 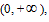 thus all P ∼ V straight lines could be interconnected to a curved surface. Under the condition of
thus all P ∼ V straight lines could be interconnected to a curved surface. Under the condition of 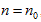 , each state point determined by P, V and T would definitely be passed through by certain straight line determined by
, each state point determined by P, V and T would definitely be passed through by certain straight line determined by 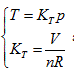 and is passed through by only one single straight line. Thus, it can be determined that the state curved surface of a closed ideal gas system is a ruled quadric surface. Similarly, the same result can also be obtained from Gay Lussac law, expressed as:
and is passed through by only one single straight line. Thus, it can be determined that the state curved surface of a closed ideal gas system is a ruled quadric surface. Similarly, the same result can also be obtained from Gay Lussac law, expressed as: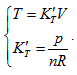 Therefore, the state surface has two groups of straight generatrixes (see Figure 1).
Therefore, the state surface has two groups of straight generatrixes (see Figure 1).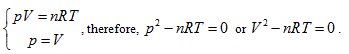
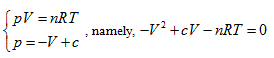



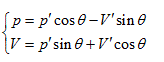
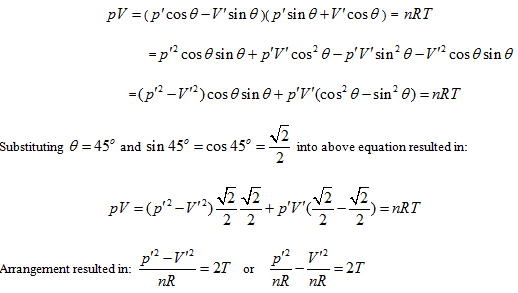
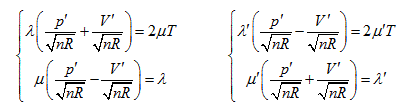
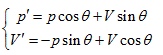
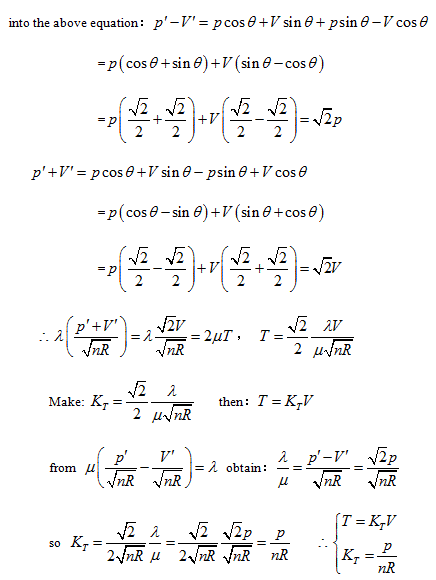
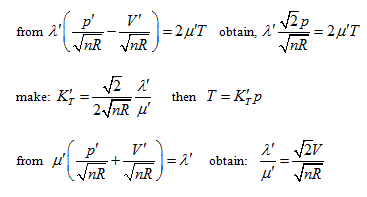
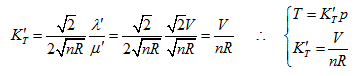
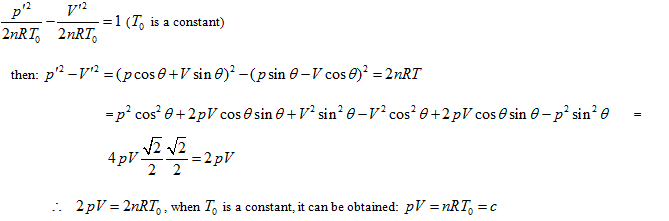
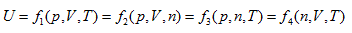

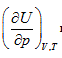 requires
requires 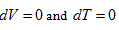 . This is the rate of intrinsic energy change with pressure in the open isosteric system with constant temperature. The open isosteric system means the artificially specified space of a research system. The specified space is considered as the research system, and the outside of this space is the environment. The exchange of substance and energy can be realized between the system and environment. With the consideration of the influence of “heat convection” in the open system, the amount of heat exchange of an open system should be the function of gas amount and temperature of the system, according to the definition of heat capacity:
. This is the rate of intrinsic energy change with pressure in the open isosteric system with constant temperature. The open isosteric system means the artificially specified space of a research system. The specified space is considered as the research system, and the outside of this space is the environment. The exchange of substance and energy can be realized between the system and environment. With the consideration of the influence of “heat convection” in the open system, the amount of heat exchange of an open system should be the function of gas amount and temperature of the system, according to the definition of heat capacity: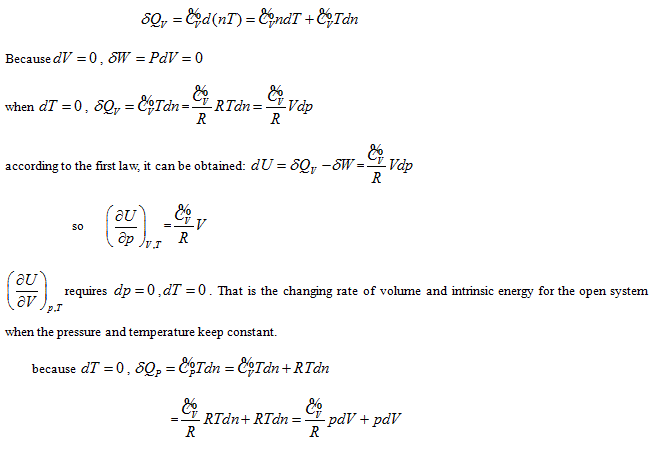
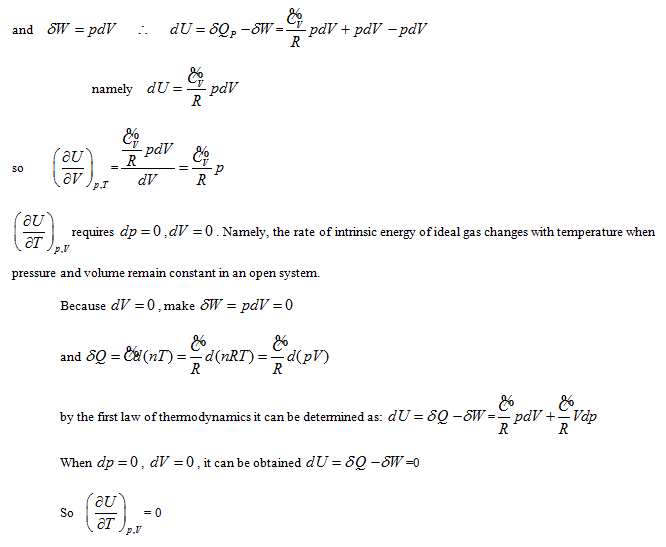
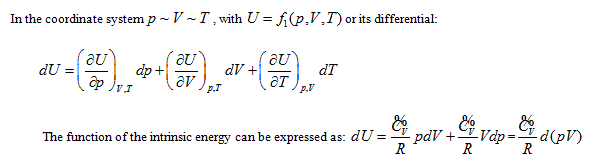
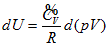 illustrates that the intrinsic energy of the system can be determined by the product of pressure and volume in the coordinate system p∼V∼T. The intrinsic energy of the system varies with the rectangular planar area within the plane p∼V surrounded by the four straight lines axis P and V as well as
illustrates that the intrinsic energy of the system can be determined by the product of pressure and volume in the coordinate system p∼V∼T. The intrinsic energy of the system varies with the rectangular planar area within the plane p∼V surrounded by the four straight lines axis P and V as well as 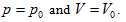
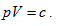
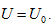 . The surface generatrix is
. The surface generatrix is 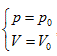 , namely, the geometric significance of
, namely, the geometric significance of 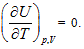 The intersecting line of the equal-intrinsic energy surface and the state curved surface
The intersecting line of the equal-intrinsic energy surface and the state curved surface 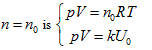
 . It can be differentiated as:
. It can be differentiated as:
 , and it is differentiated as:
, and it is differentiated as: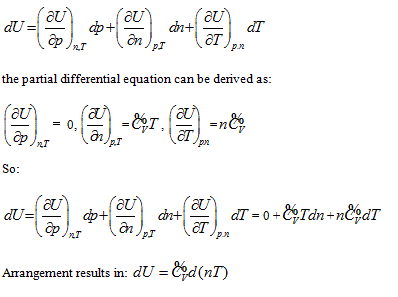
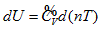 means that the system intrinsic energy can be determined by the product of gas volume and temperature in the coordinate system p ∼ n ∼ T. The intrinsic energy value of the system is proportional to the area of the rectangle formed by axis n, axis T, n = no, and T = Tofour straight lines in the n ∼ T plane.
means that the system intrinsic energy can be determined by the product of gas volume and temperature in the coordinate system p ∼ n ∼ T. The intrinsic energy value of the system is proportional to the area of the rectangle formed by axis n, axis T, n = no, and T = Tofour straight lines in the n ∼ T plane. . It is differentiated as:
. It is differentiated as:
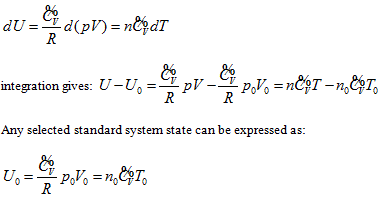
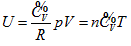
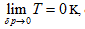 , of the coordination system.
, of the coordination system.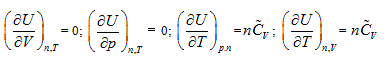
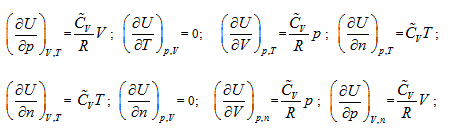
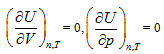 into Maxwell equation, and it has no direct relationship with the second law. Based on its containment of thermodynamics content and reasonable connection, the continued equality described herein is smoothly incorporated into the current theory system.
into Maxwell equation, and it has no direct relationship with the second law. Based on its containment of thermodynamics content and reasonable connection, the continued equality described herein is smoothly incorporated into the current theory system.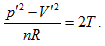 The equal intrinsic energy surface of ideal gas in three-dimensional property coordinates is perpendicular to P ∼ V plane or the inverse surface of the n ∼ T plane. Curved surface equation of intrinsic energy is
The equal intrinsic energy surface of ideal gas in three-dimensional property coordinates is perpendicular to P ∼ V plane or the inverse surface of the n ∼ T plane. Curved surface equation of intrinsic energy is 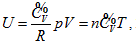 known as continued equality which includes all the basic theories of the ideal gas. Among the twelve partial differential equations derived from continued equality, Joule’s law only includes four of them, but excludes the rest eight, which indicates that Joule’s law has both verifiability and falsifiability. The detail experimental verification on the continued equality will be described in the subsequent article [13].
known as continued equality which includes all the basic theories of the ideal gas. Among the twelve partial differential equations derived from continued equality, Joule’s law only includes four of them, but excludes the rest eight, which indicates that Joule’s law has both verifiability and falsifiability. The detail experimental verification on the continued equality will be described in the subsequent article [13].