Editorial
In interstellar space, the particle density is low, and consists mainly of small molecules and fast ions [1]. Thus, much of the chemistry that occurs deals with the collision of a fast ion projectile interacting with a relatively slow moving atom or molecule, or an ion derived from one. In such a collision, the energy transfer that drives the chemistry is from kinetic energy of the projectile to electronic energy of the target.
To understand the chemistry in such systems, the details of the energy transfer from the projectile to the target needs to be understood.
Generally, the electronic energy deposition by a fast ion with velocity v in a target of scatterer particle density n is described by the equation for the stopping power, or energy transfer per unit projectile path length to the target:

S (v) is referred to as the stopping cross section of the target and, in the Bethe approximation
[2] which assumes the projectile velocity is much larger than the target electron velocities, is given by:
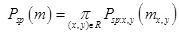
Here z1 and z2 are the projectile charge and target electron number, respectively, and I0 is the target mean excitation energy, The mean excitation energy is defined [3] as the first energy weighted moment of the target dipole oscillator strength distribution:
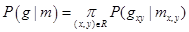
and is the determining factor for the amount of electronic energy deposited in a target by a fast ion. Thus, for electronic energy deposition by a fast ion at a given velocity in a target, the larger the mean excitation energy of target, the less electronic energy will be deposited. It should also be noted that the target may fragment or some projectile energy may be transferred to the target fragment nuclear kinetic energy, but those possibilities are not considered here.
The determination of the mean excitation energy of the target system, including the structure of the dipole oscillator strengths, therefore determines the amount of energy transferred from the projector to the target.
Several of the situations mentioned above have been previously been calculated. For example the mean excitation energies of several atomic ions have recently been calculated [4] using the polarization propagator scheme and in the dipole length approximation [5]. As an example, the mean excitation energy of the carbon atom and its ions are presented in Table 1 [4]. Note that I0 increases with ion charge, which, according to equation 2, indicates that the energy absorbed from a projectile at a given velocity decreases with target atomic charge.
Table 1. I0 (eV) of Carbon and its Ions [4]
|
I0 (eV) |
C |
65.9 |
C1+ |
92.6 |
C2+ |
134.8 |
C3+ |
214.2 |
C4+ |
486.2 |
C5+ |
539.5 |
Table 2. Mean Excitation Energies of Neutral Methane and its Stable [6].
|
I0(eV) |
CH4 |
43.47 |
CH41+ |
48.92 |
CH42+ |
54.11 |
A similar situation is found with molecular ionic targets [6]. In Table 2 are presented the calculated mean excitation energies for methane and two of its stable cations in their minimum energy geometries. Again, the mean excitation energy increases with charge, and so the ions will absorb less projectile energy with increasing charge.
The additional complication introduced when the target is a molecule is that the target has structure. As a change in target geometry will change the target dipole oscillator strength distribution, such a change will also alter the target mean excitation energy. Assuming that the targets in interstellar space are of low density and seldom undergo collision induced geometry changes, mean excitation energies reported here were calculated at the isolated target at its minimum energy geometry. The orientation of the incoming projectile trajectory with respect to the target molecular orientation could also affect the mean excitation energy of a polyatomic target. However, this does not appear to be the case.
The collision situation which has not been characterized, but which could well occur in interstellar space is the case where the projectile is a polyatomic ion which can then collide with an atomic or molecular charged or neutral system, and deposit energy into it. Again, the energy transfer will be described by a mean excitation energy of the target, but the reaction may be somewhat more complicated.
Consider first the case where the target is monatomic and thus has no orientational characteristics. It is clear that in this case the orientation of a polyatomic projectile with respect to the projectile trajectory will govern the details of the order and details of how each of the projectile atoms collides with the target. In other words, orientation may well effect the mean response of the target to collision with such an oriented projectile.
The situation would become even more complicated if the target were also a polyatomic molecule or ion.
The case where the projectile and target are polyatomic needs to be addressed.
References
- Martinez O Jr., Snow TP, Bierbaum, Kwok S, Sandford S (2008) Ion Chemistry in the Interstellar Medium. Proc IAU Symposium 251: 139-140. [crossref]
- Bethe H (1930) Zur Theorie des Durchgangs Schneller Köpuskularstrahlen durch Materie. Ann Phys (Leipzig) 5: 325-400.
- Inokuti M (1971) Inelastic Collisions of Fast Charged Particles with Atoms and Molecules – The Bethe Theory Revisited. Rev Mod Phys 43: 197-347.
- Sauer SPA, Oddershede J, Sabin JR, (2015) The Mean Excitation Energy of Atomic Ions. Adv Quantum Chem 71: 29-40.
- Oddershede J, Jørgensen P, Yaeger DL, (1984) Polarization Propagator Methods in Atomic and Molecular Calculations. Comp Phys Rep 2: 33-92.
- Jensen PWK, Sauer SPA, Oddershede J, Sabin JR (2016) Interaction of Some Molecular Ions with Fast Ion Projectiles: Mean Excitation Energies.
2021 Copyright OAT. All rights reserv